多翼式重接型电磁发射特性的研究分析

柳 敬，董 亮

(西南交通大学 电气工程学院，成都 610031)

0 引 言

电磁发射器又称电磁炮，主要包括导轨炮、线圈炮、重接炮。多翼式重接型电磁发射装置本身属于重接炮，只是抛体结构与传统板状或柱状抛体有所不同，它是一种几何互补对称机构，可提高抛体的磁稳定性。该推进装置与导轨炮和线圈炮相比，具有无接触，无烧蚀、欧姆损失相对较小、轴向加速力大、可携带大质量抛体且推进效率高等优点[1-2]。

多翼式重接型电磁发射装置的抛体形状可以不受驱动线圈间隙的限制，中间实体部分不受约束可以是任意形状有效载荷，既可以有自己的推进源像火箭，导弹驱动等，也可以是无源的普通炮弹发射。该模型在某些书籍中有相关结构介绍，但缺乏物理参数分析。本文从电容器参数的角度出发，通过建立有限元模型分别对电容电压和电容值进行多组仿真结果比较得出电容器参数对推进效率的影响规律。

1 重接型电磁发射的工作原理

图1为板状重接型电磁发射的电路图。该电路图由电源、转换装置、上下驱动线圈及抛体组成。其中电源包括电容充电器和储能电容，装换装置包括充放电开关及续流二极管，上下驱动线圈可由脉冲电容通过对开关的控制进行充电和放电进行励磁产生瞬变磁场，抛体在变化磁场中感生涡流，变化的磁场与涡流相互作用产生电磁推力，从而推动抛体向前运动[3]。

图2为板状重接型电磁发射的原理图。A～D为抛体在通电驱动线圈中的运动过程，由图可知其运动过程用一句话描述为：重接炮是利用抛体后沿被截断的磁力线在重新接合后所具有的“拉直”趋势来推动抛体向前运动[4-6]。实则是涡流与电磁场产生的电磁推力推动抛体前进。当抛体完全驶出驱动线圈时即不受电磁力的作用，若要抛体更高的出口速度，可往复此过程进行多级加速。多翼式重接型电磁发射的工作原理与板状重接炮相同，可理解为将多翼式重接型电磁发射装置的一个侧翼等效为板状抛体。

图1 板状重接型电磁发射的电路图

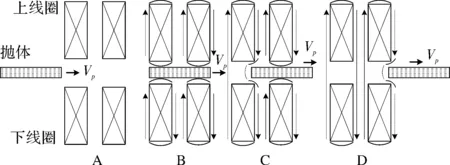
图2 板状重接型电磁发射的原理图

2 重接型电磁发射的电路方程及运动方程

2.1 电路方程

重接型电磁发射工作在C、D过程时电流通过二极管进入续流状态，此时的电路方程可表示为

式(1)求解得

式中，L为驱动线圈的等效电感，是一个随抛体位置和时间变化而变化的空间变量；R为驱动线圈的等效电阻；I0和L0分别为电路的初始电流和初始的等效电感。电感储能为

Em=Li2/2

(3)

将式(2)代入式(3)

式中,Em0为驱动线圈的初始储能。

2.2 运动方程

由于驱动线圈等效是一个随时间和抛体位置变化的空间变量，可定义其随抛体位置变化的物理感梯度为

抛体所受的电磁力通过计算[7-12]

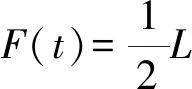
(6)

a(t)=F(t)/m

(7)

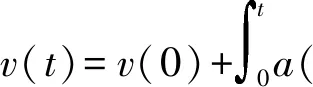
(8)

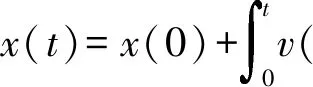
(9)

式中,a(t)、v(t)、x(t)分别为抛体运动的加速度、速度、位移；v(0)、x(0)为抛体的初始速度和初始位移；m为抛体的质量。

抛体运动的过程实则是驱动线圈中储存的能量部分转换为抛体的动能的一种能量转换形式，转换效率表示为

式中,vp、v0分别为抛体运动的出口速度和初始速度；c、u分别为电容值和电容电压

3 仿真建模与分析

3.1 仿真建模

由上小节式(10)中转换效率的表达式可以看出，电容器参数c、u的大小对抛体的出口速度和推进效率影响很大，由此对电容器参数的仿真分析变得尤为重要。

本文采用电磁分析软件Infolytica MagNet和电磁场有限元软件Ansys Ansoft Maxwell 3D进行联合仿真分析，在Ansoft Maxwell 3D软件中搭建三维模型后，导入到Infolytica MagNet软件中进行外电路编辑和瞬态3D运动求解，具体仿真参数如表1所示。

本文取四侧翼的重接型电磁发射模型为研究对象，如图3所示，每个侧翼左右并排两个驱动线圈提供电磁能驱动抛体运动。图4为根据图1编辑的仿真外电路，为了保证每组驱动线圈的有效“重接”，需使线圈的电流方向一致。

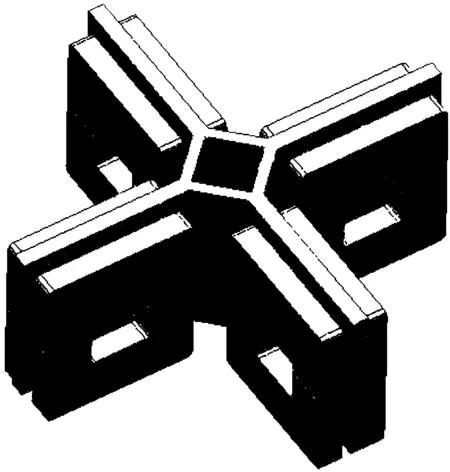
图3 四翼式重接型电磁发射的三维模型

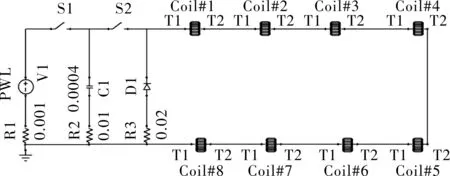
图4 仿真外电路

组件参数参数值驱动线圈材料绕制铜线横截面积/mm2径向厚度/mm外尺寸/mm∗mm内尺寸/mm∗mm与抛体间隙/mm匝数铜415100∗10040∗40248抛体材料有效翼长/mm径向厚度/mm高度/mm初始位置/mm质量/kg初始速度/(m·s-1)铝11210100111.510

3.2 仿真分析

根据表1中的仿真参数，采取控制变量的思想，保持电容值400μF一定，图5～图7为电容电压在15 kV、20 kV、25 kV、30 kV、35 kV、40 kV下的驱动线圈电流曲线、轴向加速力和出口速度曲线。在图6中取任意电压下的轴向力进行分析，抛体在运动的过程中受到正向加速力和负向减速力的作用，而正向加速力远大于负向加速力，使得抛体向着同一方向运动。由于电容值一定，所以电容放电时间保持不变，随着电容电压的增加，每组线圈中产生的涡流增加，因此抛体受到的电磁力增加，正负加速力峰值时间均提前产生，出口速度增加。从图5电流曲线可以看出，在电压值较大的情况下，电流值在先增大后减小后又上升了一段，分析原因是抛体在出口时线圈电流对抛体涡流的减小有一定的阻碍作用。表2为不同电容电压下的出口速度和能量转换效率的比较。可以看出当电容值恒定时，存在特定的电容电值使得系统的能量转换效率最高 。

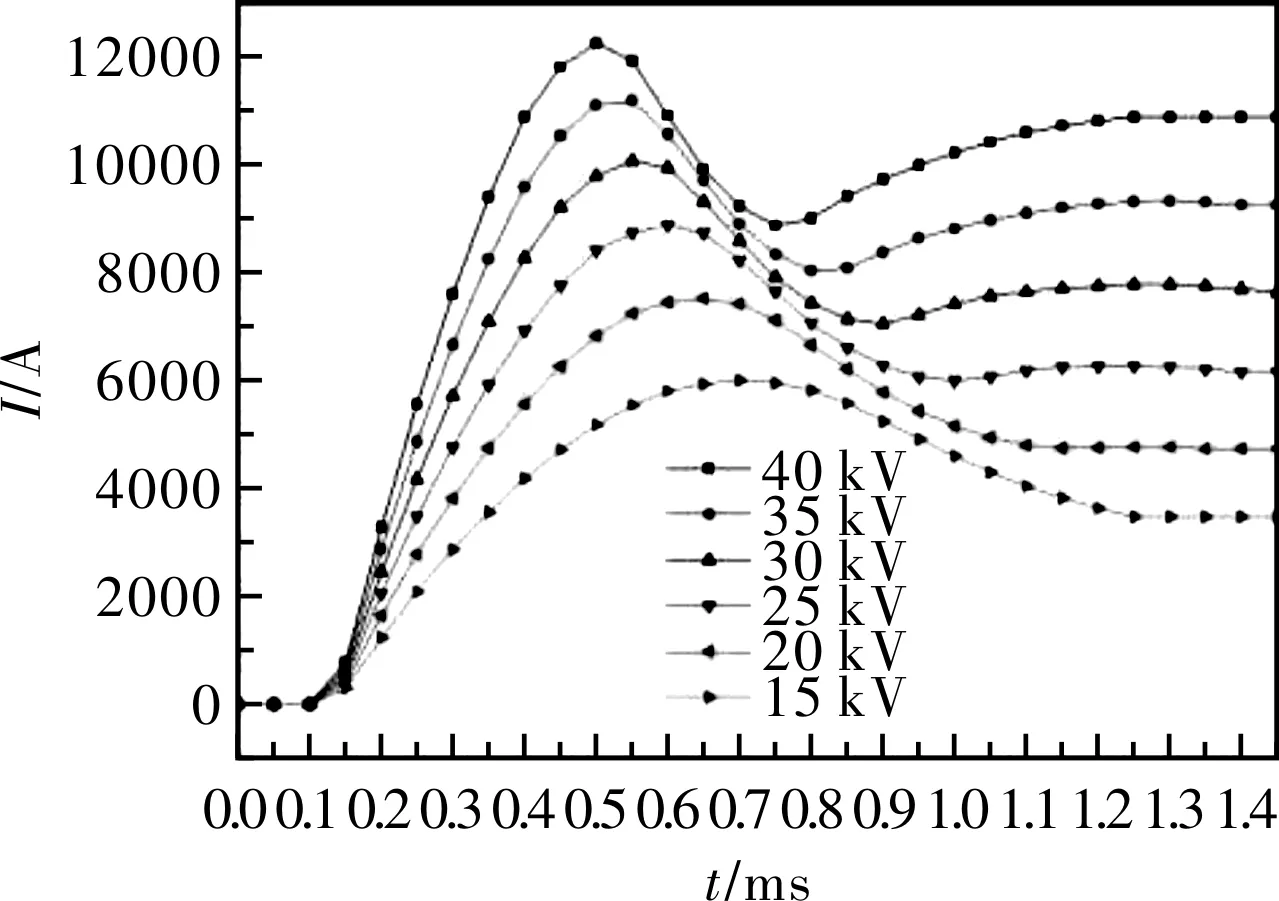
图5 线圈电流随时间变化曲线图

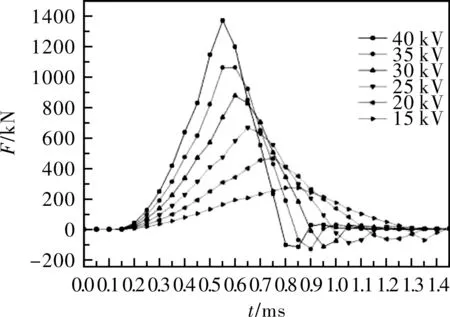
图6 轴向力随时间变化曲线图

图7 速度随时间变化曲线图

电容电压/kV抛体的出口速度(m/s)能量转换效率1597.015.79%20134.116.22%25166.616.76%30195.215.98%35222.915.31%40246.114.29%

保持电容电压25 kV一定，图8-10为电容值在300 μF、350 μF、400 μF、450 μF、500 μF、550 μF下的驱动线圈电流曲线、轴向加速力和出口速度曲线。随着电容值的增加，放电时间常数增加，脉冲电流上升时间变长，电流峰值变大。增大电容值使得放电速率减缓但增加了电荷的释放量，这样在抛体上感生的涡流变强，从而使得轴向加速力变大，出口速度增加。图8中的大电容情况下最后线圈电流出现畸变情况与图5类似，都是线圈电流对抛体涡流减小的阻碍作用。表3为不同电容值下的出口速度和能量转换效率的比较，与电容值恒定，不同电容电压下情况类似，电容值增加，出口速度增加，而能量转换效率先增大后减小。也就是说，存在最优电容值使得系统的能量转换效率最高。

通过对电容器参数的仿真优化可以看出，增大电容值或者电压值都能使得抛体的出口速度增加，但能量转换效率并不是一直增加，而是先增大后减小。保证两个参数中的任意一个不变，都存在另一个最优参数值使得能量转换效率最高。

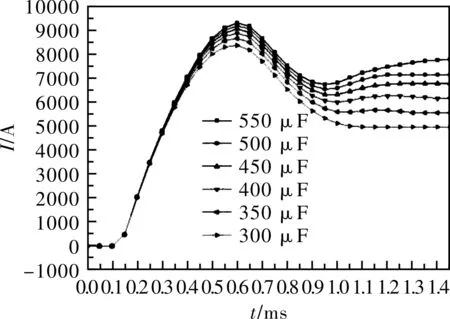
图8 线圈电流随时间变化曲线图

图9 轴向力随时间变化曲线图

图10 速度随时间变化曲线图

电容值/μF抛体的出口速度(m/s)能量转换效率300142.016.24%350155.016.58%400166.616.76%450171.015.70%500174.814.76%550179.514.15%

4 结 论

(1)电容器参数对抛体的出口速度，轴向加速力，驱动电流，能量装换效率都有很大的影响。通过本文的仿真模型及参数可以看出，存在最佳电容器参数组合25 kV，400 μF使得系统的转换效率最高达到16.76%，最大出口速度为166.6 m/s。

(2)由于不同电容器参数下的欧姆损耗不同，使得最大出口速度不一定对应最大能量转换效率，在实际的电磁发射过程中，若要使得抛体加速性能最佳，需通过仿真分析计算出最佳的电容器参数组合。

(3)与传统的LCR过阻尼振荡放电不同，由于抛体涡流与驱动线圈之间存在变化的互感，驱动线圈电流的变化受到抛体中涡流变化的影响。

(4)当出现多级加速时，由于每一级中抛体在线圈中的渡越时间逐渐缩短，需保证电流放电时间更短，一般采取增加电压减小电容的方法使得抛体在高速发射的过程中获得更高的加速性能。