双层分数槽绕组永磁同步风力发电机的设计与仿真

李 争，杜 磊，杜深慧，李 莹，李建军

(1. 河北科技大学 电气工程学院，石家庄 050018; 2. 河北新四达电机股份有限公司，石家庄 052160)

0 引 言

能源短缺一直是困扰世界的一个难题。随着经济社会的发展，煤炭资源日渐枯竭，对清洁、可再生新能源技术的开发利用需求迫切。风力发电作为目前最有商业开发潜力的新能源技术，自21世纪以来得到了迅猛发展。永磁同步风力发电机由于其结构简单控制灵活，是一种应用广泛的交流电机。现代社会中使用的交流电能几乎全部是有同步发电机产生的并在风力场中得到了广泛应用。永磁同步发电机是一种结构特殊的同步发电机，其优点很多。与普通同步发电机相比，主磁场由永磁体产生，省去了励磁绕组，磁极铁心和电刷-集电环结构，可靠性大大改善，减少了机械摩擦损耗，提高了发电机的效率[1-2]；另外在风力发电机组的轴上直接将永磁同步发电机接上，在低速运转下保持较高的发电功率[3]；张岳等人利用Ansoft软件磁路法模块Rmxprt对2MW凸极形式的永磁同步风力发电机的定转子和永磁体尺寸进行参数化的优选，设计出永磁电机合理的方案[4-5]。张炳义等人设计了一种新型表贴式磁极结构，可以有效改善气隙磁密波形的正弦度，削弱反电势中的谐波含量，降低电机的谐波损耗和纹波转矩，提高电机的效率和运行平稳度[6-7]；许实章指出若采用每极每相槽数q等于分数的绕组，即分数槽绕组一方面能利用分布效应削弱由于磁极磁场的非正弦分布所感应的谐波电势，另一方面也使齿谐波电势的次数较低而幅值较大[8-10]。

结合以上文献指出的永磁同步发电机的优点，本文提出一种双层分数槽绕组的永磁同步发电机。 利用有限元软件对其进行静态和瞬态的仿真分析，最后得出发电机的电势、磁链、转矩等参数。其结果为进一步优化设计方案提供理论参考。

1 双层分数槽绕组永磁同步风力发电机的结构和原理

1.1 电机结构

永磁同步发电机结构多样，本设计电机本体包括定子，绕组，转子，永磁体4部分。转子采用径向式转子磁路结构，其永磁体离气隙较近，漏磁系数小，每极气隙磁通仅由一个永磁体提供，由此可得气隙磁密相对较小制作工艺简单，易于Ansoft仿真。绕组采用双层分数槽绕组，采用分数槽一方面利于利用分布效应削弱由于磁极磁场的非正弦分布所感应的谐波电势，另一方面也使齿谐波电势的次数较低而幅值较大；而采用双层，则线圈节距可调，可采用适当的短距系数削弱电势谐波，改善电磁性能。永磁体由钕铁硼材料烧结而成，采用表面式内转子凸出式转子结构。定子铁心由0.5 mm厚的硅钢片制成以减少铁耗，定子槽采用半闭口式，可有效削弱齿谐波电动势和齿槽转矩。双层分数槽绕组连接图如图1所示。

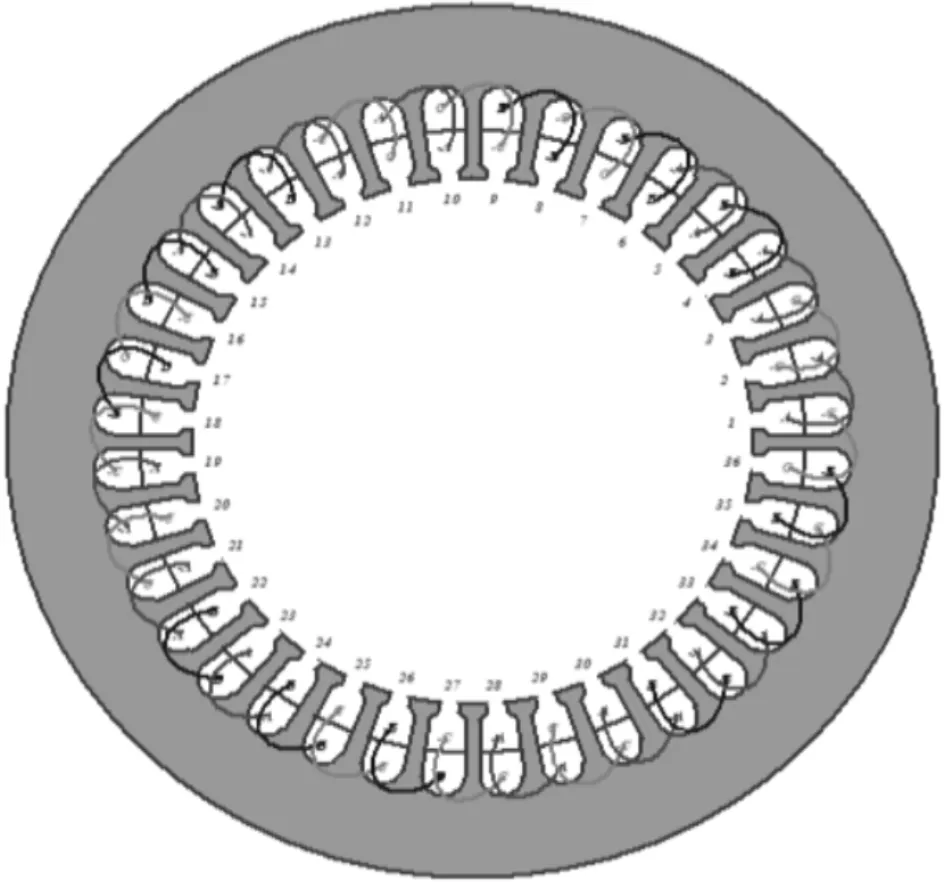
图1 双层分数槽绕组连接图

1.2 发电机基本参数的确定

本文所设计的为小型风力发电机，采用极对数p=10，定子槽Z=36，并联支路数为2，额定功率为3KW，额定电压为220V,m=3的三相永磁同步发电机为模型，由公式：

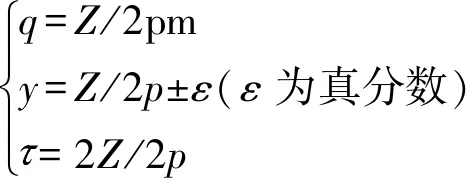
式中，q为每极每相槽数；y为线圈节距；为极距。

得：q=3/5,y=1,=9/5y<,即短距绕组。

在现实条件下，发电机的转动依靠风量来拥有转动动能，发电机的转动和风量有着不可分割的关系，在正常理想状态下，发电机的转速应与风量成正比关系，即风速越大风机的转动速度越快，但是在现实条件下，小于3 m/s时，由于发电机自身的摩擦，不会转动，启动风速为3 m/s,运行风速范围为3 m/s～22 m/s，当风速大于22 m/s，发电机处于抱死状态，不会转动，模拟风速与发电机转速曲线关系如下图2所示。本文所涉及发电机参数如表1所示。

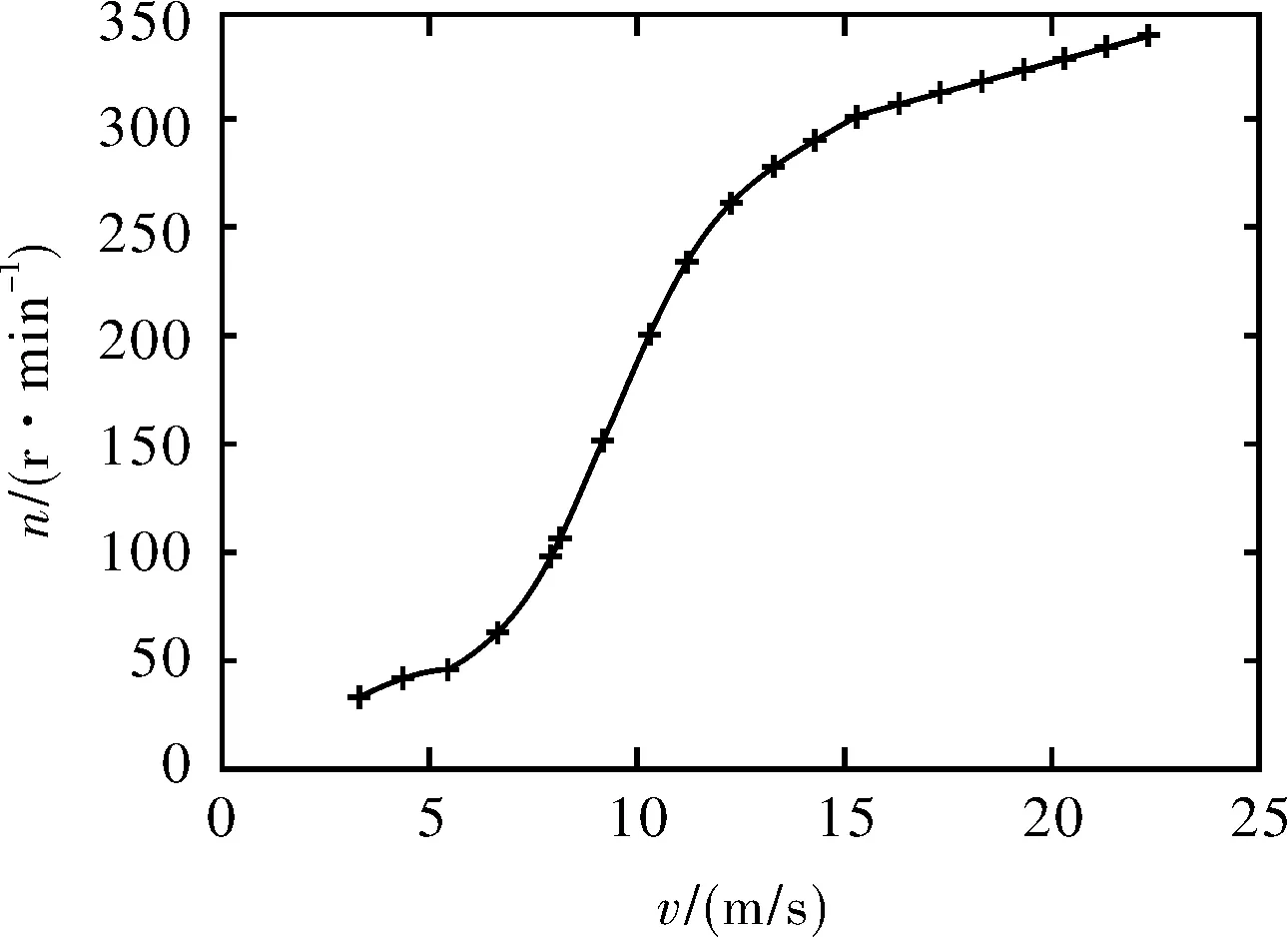
图2 风速与发电机转速对应曲线

参数名称参数值额定功率/kW3并联支路数2磁极对数10额定电流/A7.89定子内径/mm107.9转子内径/mm25额定电压/V220额定转速/(r/min)300矫顽力/(kA/m)890定子外径/mm142.25转子外径/mm102.44永磁体外径/mm107.4

此发电机与普通电机相比优点如下：

(1)采用多级结构，使发电机较易达到额定转速300 r/min。

(2)线圈的节距小于极距，端部绕组缩减明显，节约成本，降低铜耗。

(3)由于每极每相槽数q=Z/2Pm为分数,即采用分数槽绕组，可有效消除永磁电机中由齿槽效应引起的脉动力矩。

2 双层分数槽绕组永磁同步风力发电机的解析法分析

将二维极坐标(r,θ)固定在定子上，且以ns槽的中心作为初始位置，β为槽宽角，第i槽的起始位置定义如下：

定义如下两个函数，利于谐波系数的求解和子域通解的表达：

在二维极坐标中，磁感应强度的径向和切向分量为

双层分数槽绕组永磁同步风力发电机的求解域可分为：定子槽、气隙、永磁体。其中气隙子域和永磁体各一个，本文分析的为双层绕组2ns个。其中转子内表面半径为R1,永磁体表面半径为R2。定子槽底半径为R3,定子外径为R4。

2.1 槽子域子域分析

由于上下层电流密度分别对应上下层线圈边，因此每个槽子域应当划分为独立的子域。为了使上下层面积相等，令

分别用Alit、Alib表示第i槽上、下层边的矢量磁位，则泊松方程表示如下：

2.2 气隙子域分析

在气隙子域中，无电流密度分布也无磁化强度分量，因此拉普拉斯方程：

▽2A=0

(6)

气隙子域为环形区域，其矢量磁位方程为

根据分离变量法，矢量磁位A2(r,θ)表示为

A2(r,θ)=R(r)Θ(θ)

(8)

将式(8)代入式(7)可得：

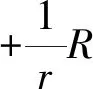
(9)

即:

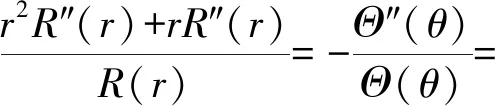
(10)

常数λ为特征值，结合式(7)得到两个常微分方程的定解问题:

与

r2R″(r)+rR′(r)-λR(r)=0

(12)

特征值分别为λ0=0，λn=n2，对应的特征函数分别为Θ20(θ)=A0、Θ20(θ)=Ancos(nθ)+Bnsin(nθ)

由于特征值为λ0、λn，可得通解为

经线性叠加式(7)得拉普拉斯方程通解如下：

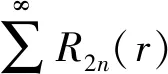
(14)

又因为沿气隙子域中任一半径R处画一圆圈，所在的区域内通过的总净电流为0，因此式(7)的原始通解形式不含直流项。结合式(2)，最后通解为

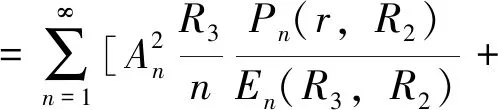
(15)

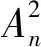
2.3 永磁体子域分析

在永磁体子域中，无电流密度分布有磁化强度分量，因此泊松方程为

▽2A=-μ0▽×M

(16)

永磁体子域矢量磁位的偏微分方程如下：

式中，Mt、Mθ分别为永磁体剩余磁化强度径向切向分量。在得到三类子域通解的基础上，需要根据各子域在径向方向上的磁场磁场连续关系即法向磁密相等和切向磁场强度相等得到相关谐波系数[11]。

2.4 气隙磁密分布

本文以双层分数槽绕组永磁同步风力发电机为例，由式(3)可知，气隙子域中磁感应强度的径向分量为

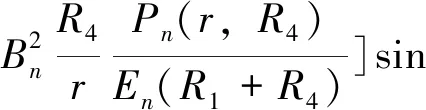
(18)

图3为通过解析法得到的气隙磁密径向计算结果，一个周期内有十个波峰，十个波谷，其分布位置、曲线的走势与图8有限元法所得的气隙径向磁密仿真结果近似相符，解析法所计算的波峰值比有限元法所得的波峰值略小，除了有计算误差的影响之外，另外在有限元法计算中，对发电机的剖分过于精细。有限元法对发电机永磁体气隙磁密的仿真波形与解析法算出的仿真波形基本一致，充分验证了解析法建立的转子永磁体模型的准确性。

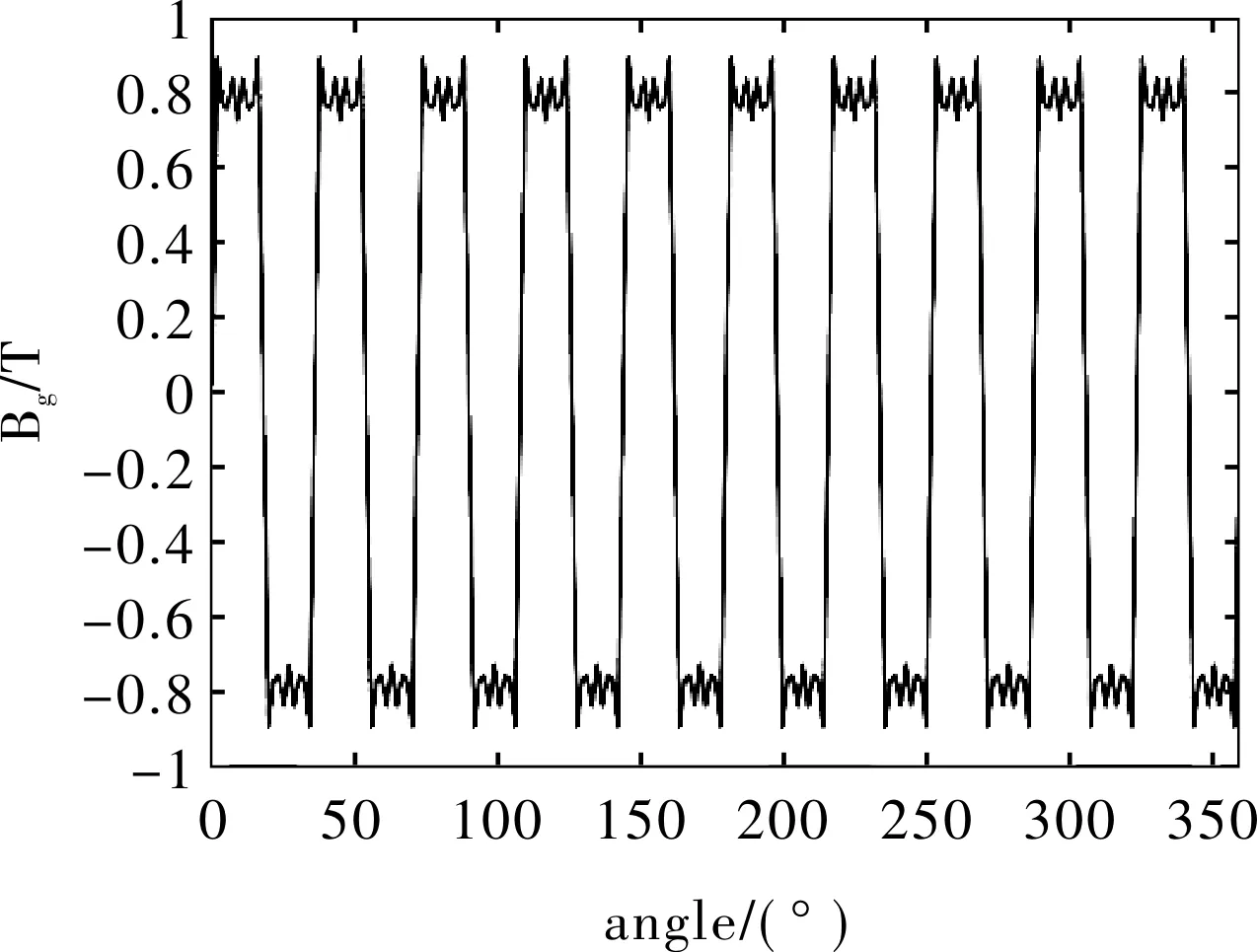
图3 气隙磁密BgAir的径向分布(解析法)

3 双层分数槽绕组永磁同步风力发电机的磁场分析

为了求出场量与场源之间的关系，以达到分析磁场的目的，通常引进位函数作为辅助变量，以减少变量数。一般求解区域内存在电流，需要引入空间坐标的函数，即:矢量磁位A。不计发电机外部磁场，忽略位移电流的影响，电流密度和磁失位只有Z轴方向的分量，磁感应强度与矢量磁位满足关系式如下：

B=▽×Az

(19)

则有：

(20)

式中，Jz为电流密度；μ为磁导率。

又有：

▽×(▽×Az)=μJz

(21)

利用恒等式：

▽×(▽×Az)=▽(▽·Az)-▽2Az=-▽2Az

(22)

得：

▽2Az=-μJz

(23)

由此可知：想达到分析磁场的目的，引进位函数作为变量进行偏微分的求解即可。一般选取发电机外壳作为边界，才能使解唯一。本文利用有限元软件对发电机进行建模，分别采用瞬态和静态求解器对上述永磁同步风力发电机进行电磁场分析。

3.1 静态分析

3.1.1发电机模型的建立与磁场分析

本文利用静态求解器建立发电机的二维模型，其基本流程为：建模-定义材料及分配-设定激励源及边界条件-网格剖分。模型建好后，进行求解残差设定，即设定计算的迭代步数，求解收敛误差值和每次更新的单元百分比，最后对发电机进行静态分析，经过4步自适应求解，系统的误差小于1%，达到了预期的目标。

其中求解域为整个发电机的横截面，静态平面的电磁场满足以下泊松方程边界：

式中，Ω为求解区域；Γ1为第一类边界条件；Γ2为永磁体等效面电流边界；Jm为永磁边界等效面电流密度；μ1、μ2为永磁边界两种介质的磁导率。

把定子外表面和转子内径表面Γ1设为边界面即施加磁通平行边界条件，发电机无边界漏磁存在，令其上的矢量磁位Az=0。

建模结果如图4所示，网格剖分结果如图5所示。发电机磁场分布如图6所示。发电机矢量B的分布情况如图7所示。

图5 网格剖分结果图

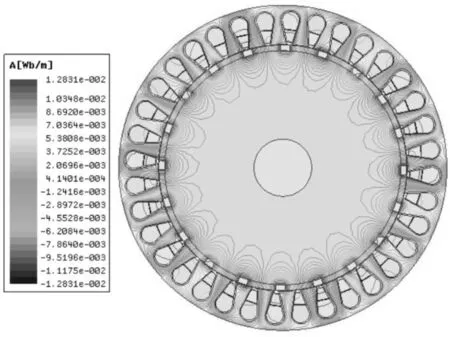
图 6发电机磁场分布图

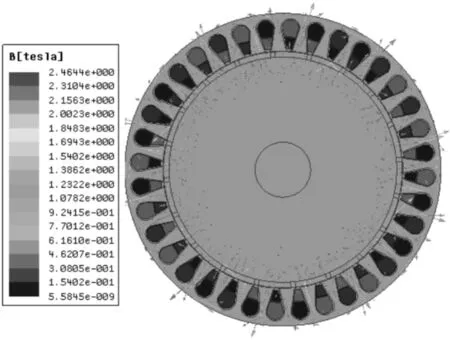
图7 发电机矢量B分布图

从图6可以看出，永磁体磁极径向布置，并直接面对气隙，永磁体发出的磁通分为主磁通和漏磁通，主磁路为：永磁体磁极-气隙-硅钢片定子齿-硅钢片定子轭-硅钢片定子齿-气隙-另一永磁体的异性磁极-硅光片转子轭-开始的永磁体[12-13]。其完成了能量的转换，发电机磁极的N级和S级交错排布，磁场相反，与实际情况相吻合。漏磁通通过漏磁路闭合。从图6可以看出，漏磁通较小，从漏磁方面观察，此设计合理。从图7可明显的看到电机主磁通路径，与上述情况相一致。

图8 发电机径向磁密

发电机径向磁密如图8所示，对其进行快速傅里叶分解即FFT，其谐波含量情况分析如图9所示。由于永磁体建立磁场，磁密在气隙间的分布波形近似于周期为360°即围绕永磁体一周674.81 mm处的平顶波，一周期内有十个波峰，十个波谷，与本文所设计的极对数p=10相吻合, 有限元法对发电机永磁体气隙磁密的仿真波形与图3解析法算出的仿真波形基本一致，充分验证了解析法建立的转子永磁体模型的准确性。

该气隙磁场谐波含量丰富，曲线波动明显。观察图9可发现，其径向磁密的基波幅值为1.082 T，基本满足设计要求。

3.2 瞬态分析

分析双层分数槽绕组永磁同步风力发电机的空载特性很关键，因为空载特性可看出发电机磁路的饱和趋势及输出电压的能力[14]。当风力驱动转子，定子线圈切割由永磁体发出的磁力线产生旋转磁场，从而感应出三相交流电势[15-17]。创建空载回路并导入，将定子绕组接高阻值电阻，图10为在Transient下建立的空载回路。

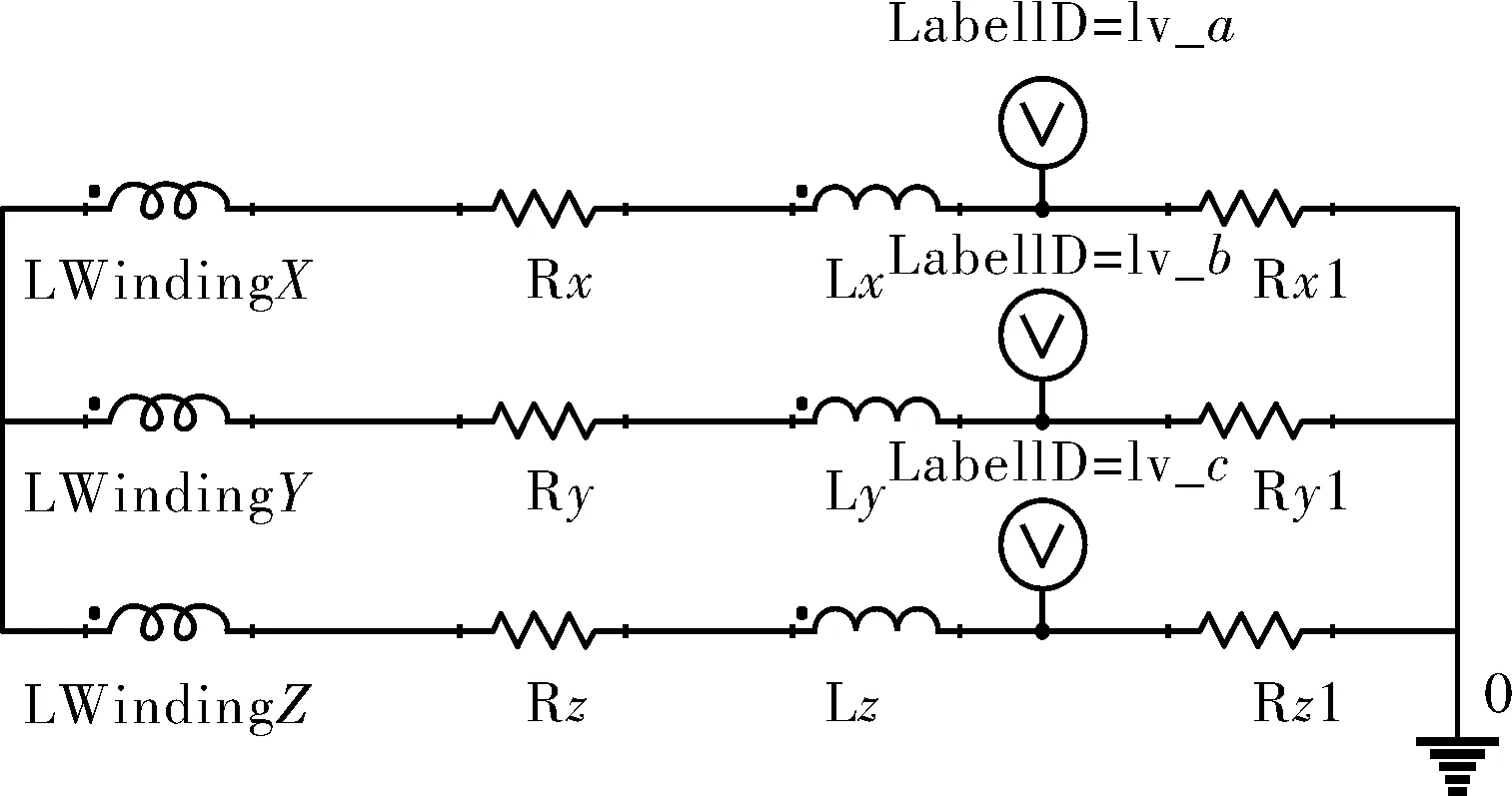
图10 空载下建立的外电路回路

基于瞬态求解器，可以求出发电机的感应电压，磁链等曲线[18-19]。其建模基本流程与静态场基本相似。不同之处在于，在瞬态场中多了一个求解时间设置，在本文中设计的求解时间为0.0002，场信息保存时间步长设置为0.001，即场求解每5步保存一次。选取0.01 s时发电机的运行状态为研究对象，此时发电机已工作稳定。图11为0.01 s双层分数槽绕组永磁同步风力发电机A、B、C三相绕组的反电势波形，可以看出电压的最大幅值为63.2 V左右，即图10中三个电压表所测的空载电压数值。由于采用均匀气隙，同时受齿谐波的影响，该发电机反电势的波峰处类似平顶，谐波含量丰富，若要消除此影响，可采用不均匀气隙和定子斜槽来减少谐波含量，此内容将在以后研究中详细说明。对反电势波形进行谐波分析，可得到反电势的基波和各次谐波幅值情况，如图12所示。

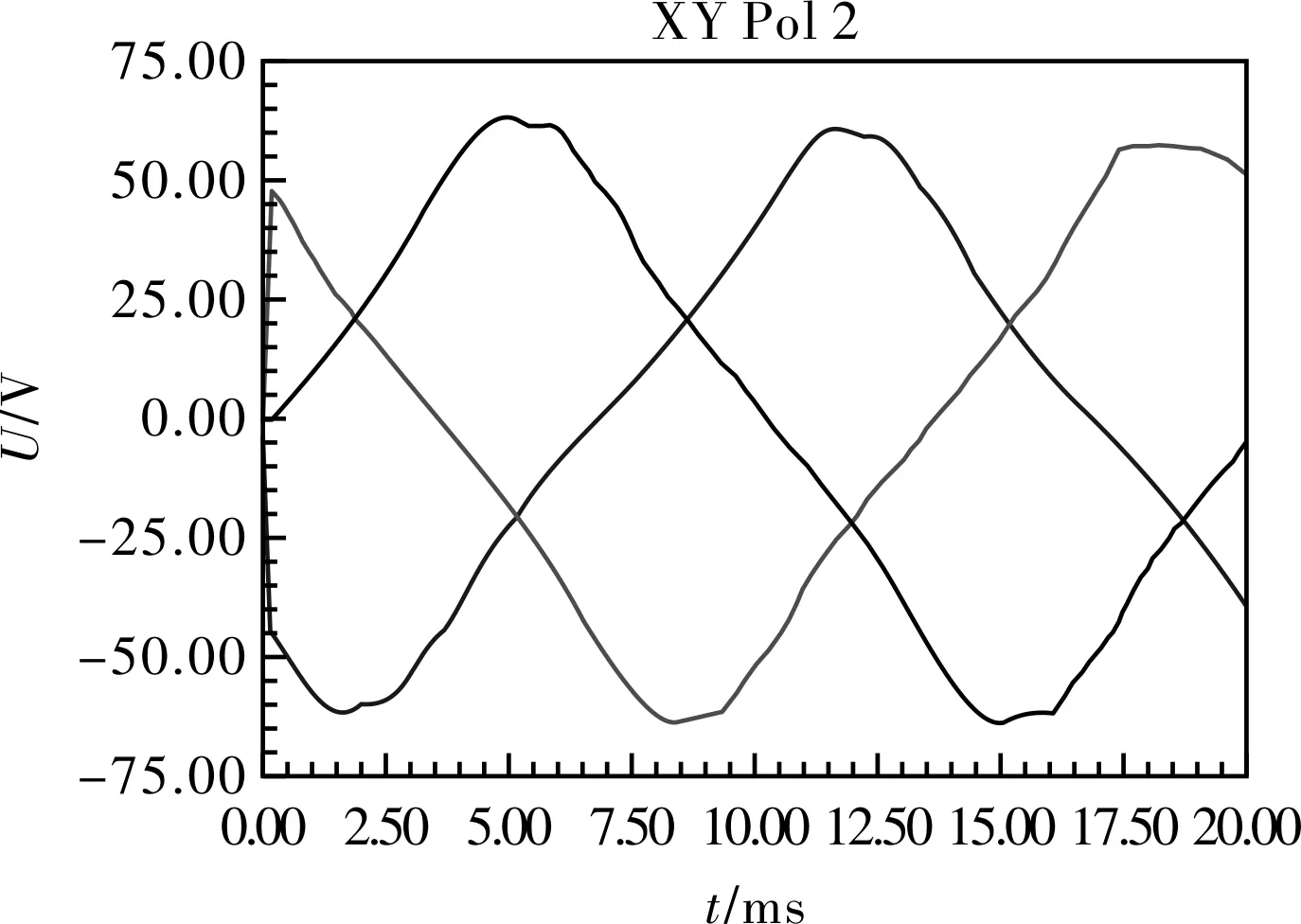
图11 三相绕组的反电势波形

图13为0.01 s时刻的磁链曲线，由于磁链的建立与产生磁通的电流有关，所以波形为幅值为0.17 Wb的正弦波。图14为电机的位置曲线图，可以看出，发电机在20 ms内转过大约50°,符合低转速发电机的要求。

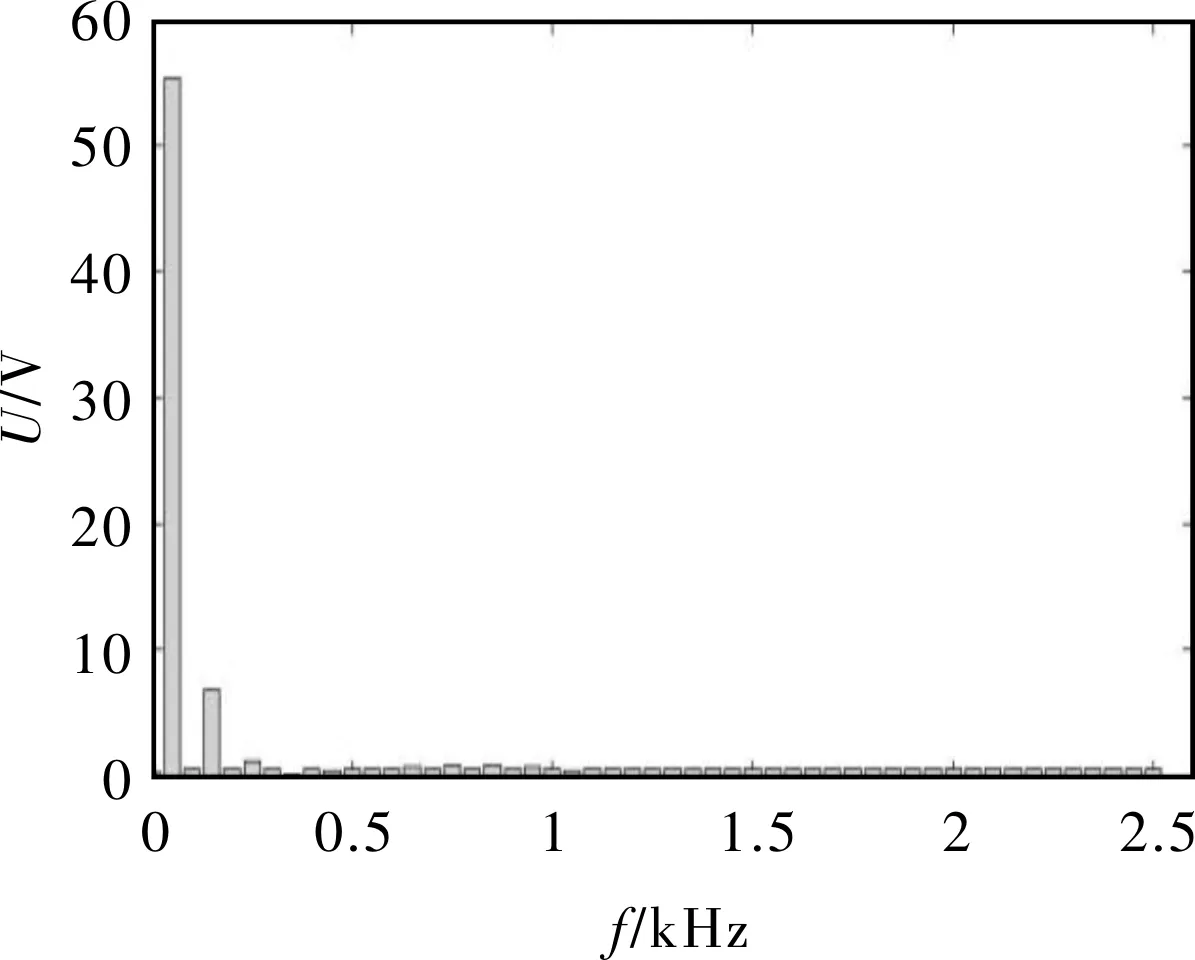
图12 反电势的基波和各次谐波幅值分布情况

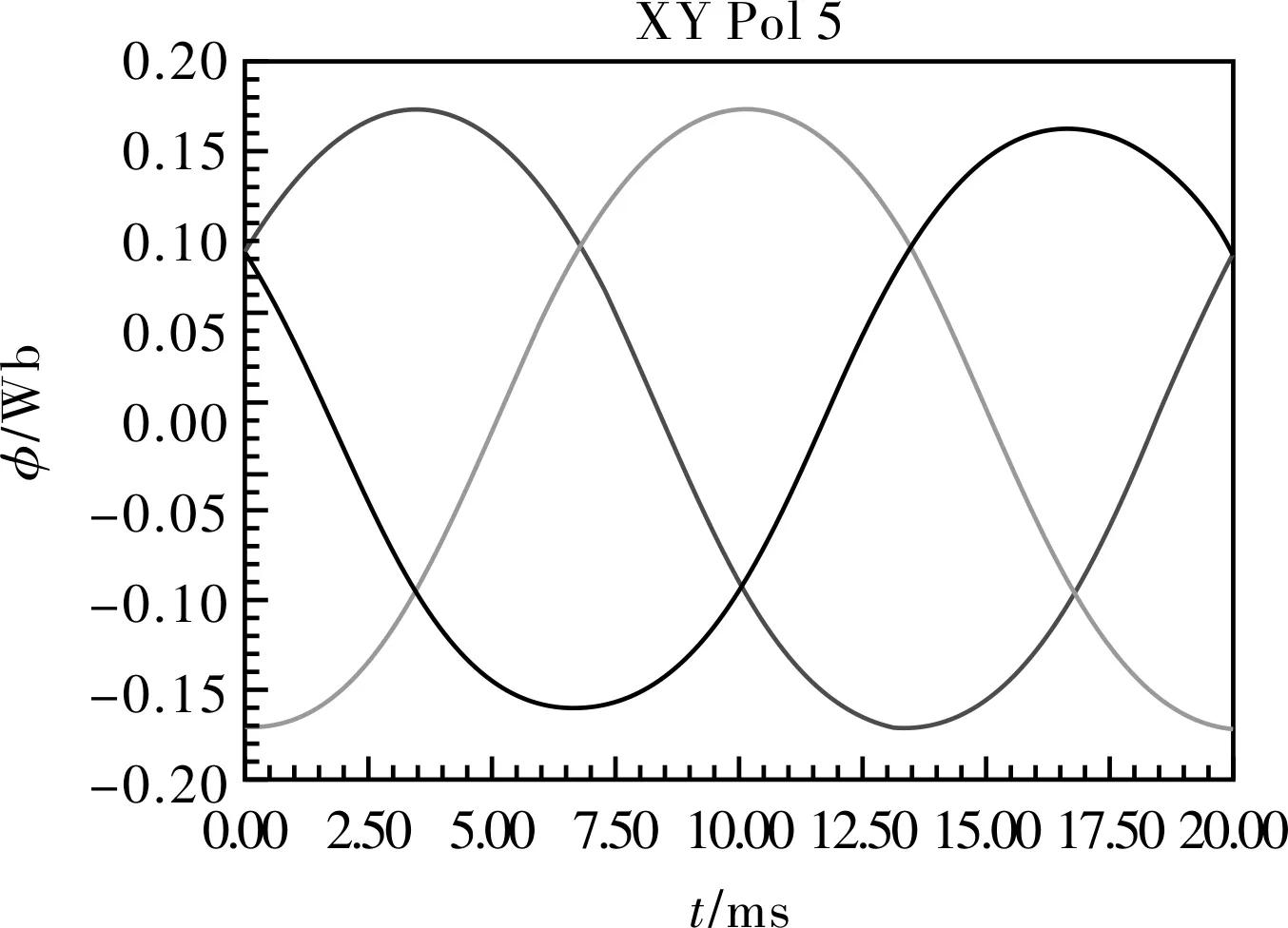
图13 0.01 s时刻磁链曲线

图14 发电的的位置曲线图

图15为0.01 s时刻的转矩曲线图，从图可分析出，在求解时间0.02 s内，随着转子转动，转矩周期性对称变化，且最大幅值为75 Nm。图16为0.01 s时刻相邻永磁体间隔长度不同的涡流损耗曲线随时间变化情况，1.5 ms时永磁体的涡流损耗达到最大，此后上下波动开始周期性变化，随着永磁体间的间隔增大涡流损耗值下降明显，可减少永磁体的发热，延长电机寿命。

图15 0.01 s时发电机的转矩曲线

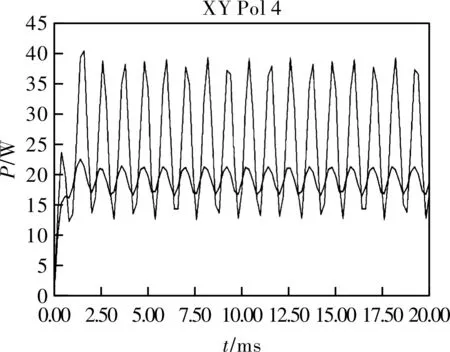
图16 涡流损耗对比图

4 结 语

本文建立双层分数槽绕组永磁同步风力发电机的模型，对其进行静态和瞬态仿真，通过分析发电机的磁场分布，发电机矢量B及反电动势，气隙磁密，涡流损耗，齿槽转矩等分布特性，验证了发电机设计的合理性。利用解析法，分析了气隙径向磁密并与有限元法相互验证，与此同时，其结果的正确性也为以后研究风力发电系统参数提供理论依据，为进一步优化提供了基础。