机动行为下飞机油箱晃动流固耦合动力学分析

2019-03-29杨尚霖陈晓峰杜发喜雷忠琦姚小虎

航空学报 2019年3期

杨尚霖，陈晓峰，杜发喜，雷忠琦，姚小虎, *

1.华南理工大学土木与交通学院，广州 510640 2.成都飞机工业(集团)有限责任公司技术中心，成都 610092

飞机在飞行过程中由于姿态变化等因素的影响会造成油箱内燃油的晃动，燃油晃动对油箱壁面造成的冲击会对飞机油箱结构安全性以及飞行稳定性产生影响，尤其在飞机执行机动飞行时，飞机整体处于大过载状态，此时的燃油晃动问题更加值得关注。

飞机油箱晃动属于航天器充液容器晃动问题，对此类问题的研究早期以理论和实验为主[1-4]，但理论和实验研究均以较简单晃动条件下的规则几何形状容器为研究对象，针对复杂结构以及复杂晃动条件下的工程应用，理论和实验研究难以满足要求，随着计算机技术的发展，数值模拟逐渐成为研究此类问题的主要手段之一。毛志祥和杨觉敏[5]通过有限元模拟证明了扩展拟弹性法可用于飞机整体油箱的液固耦合振动计算。王力等[6]用ALE(Arbitrary Lagrange Euler)法模拟了无人机发射过程中燃油和油箱的相互作用，将燃油箱简化为刚性体，得到不同充液率下无人机起飞姿态的变化和燃油晃动规律，结果表明半油起飞时无人机姿态变化最为严重，进而对油箱内部不同防晃隔板的防晃效果进行了研究。杨瑞[7]采用ALE法模拟了机翼油箱在定轴转动下的油箱晃动，并进一步对某一真实飞行工况进行了模拟。Yang等[8]通过跌落实验和ALE法模拟研究了直升机矩形油箱的跌落冲击过程，模拟结果与实验结果吻合，分析了冲击速度、冲击角度、油箱壁面厚度以及充液率对油箱动态响应的影响，结果表明油箱底角在冲击过程中最易受损。刘富等[9]结合某型飞机副油箱晃振实验，采用SPH(Smoothed Particle Hydrodynamic)法计算了副油箱在俯仰运动下燃油的晃动特性，对燃油晃动过程中的重心位置进行推导，获得了晃动过程中燃油重心变化的时间历程曲线。唐浩等[10]用SPH法对导弹发射过程中导弹燃油箱内燃油的晃动进行了仿真分析，不考虑油箱变形，得到了液面变化情况、重心变化曲线和油箱与燃油之间的相互作用力。黄愉太[11]采用SPH法对某型飞机整体油箱滚转晃动时的流固耦合效应做了初步探究。Veldman等[12]对Sloshsat FLEVO卫星进行仿真，采用基于Navier-Stokes方程的计算模型，结合VOF (Volume Of Fluid)法，取得了与实验一致的结果。Hv等[13]基于有限体积法采用VOF多相流模型对飞机副油箱内燃油晃动进行模拟，成功预测了晃动过程中作用于油箱壁面的动水压力。Farhat等[14]通过数值模拟研究了次声速、跨声速和超声速飞行时机翼副油箱内油液晃动对机翼颤振的影响。

上述研究采用ALE、SPH和VOF等方法探究了简单工况下的油箱晃动问题，均未考虑大过载复杂情况下的油箱晃动。Reddy等[15]为考虑飞机油箱在惯性力作用下结构的安全性，对惯性载荷采用静力加载方式，采用ANSYS进行静力计算，对飞机油箱在不同惯性载荷下的应力和变形进行了分析，但未能获得在惯性力作用下的燃油晃动情况以及油箱结构应力等量的变化情况。针对复杂情况下的动态强非线性晃动问题，ALE法和SPH法无法在保证效率的同时精确捕捉晃动过程中出现的液体飞溅、旋涡以及气泡等流场细节[16-17]，VOF法可准确模拟复杂晃动问题[18]，不足之处在于单一的VOF法仅能求解流场晃动特征，无法求解固体结构随晃动的响应。针对以上问题，本文基于VOF法求解液体晃动，联合有限元软件ABAQUS和流体动力学软件Star-CCM+，建立瞬态飞机油箱晃动流固耦合计算方法，以某型飞机整体油箱为研究对象，探究飞机在半滚倒转机动行为下的油箱晃动流固耦合效应，为研究飞机油箱晃动提供参考。

1 数值方法

1.1 研究对象

本文以某型飞机整体油箱为研究对象，油箱长约2 m，宽约0.6 m，高约0.6 m，油箱主要部件为框架和上、下蒙皮，其中框架为铝合金，蒙皮为复合材料，其纤维纵向为长度方向，纤维横向为宽度方向。油箱内部分为一个连通油室和一个独立油室，其部件及几何模型如图1所示，燃油采用3号喷气燃料(RP-3)，材料属性见表1～表3。

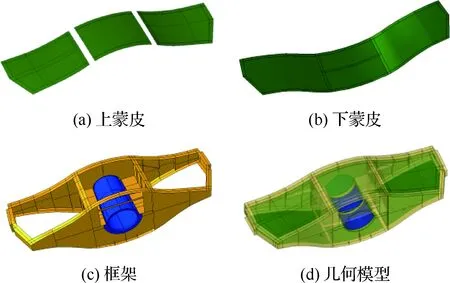
图1 油箱部件及几何模型Fig.1 Components of fuel tank and its geometry model

表1 铝合金材料参数Table 1 Material parameters of aluminum alloy

表2 复合材料材料参数Table 2 Material parameters of composite

表3 燃油材料参数Table 3 Material parameters of fuel

1.2 流固耦合计算方法

本文通过ABAQUS与Star-CCM+联合仿真进行流固耦合计算，考虑到半滚倒转机动行为下飞机油箱刚体位移远远大于油箱壁面变形量，在这种情况下燃油晃动受油箱刚体位移主导，可忽略油箱壁面变形对燃油晃动的影响，故本文采用单向流固耦合求解半滚倒转机动行为下的油箱晃动。单向流固耦合方法如图2所示，将计算模型分为流体域和结构域，通过在Star-CCM+求解流体域，获得流场压力，并在每一个时间步将获得的流场压力传递到ABAQUS结构域进行应力应变计算，可得到油箱结构在流场压力下的应力应变等量的时间历程。

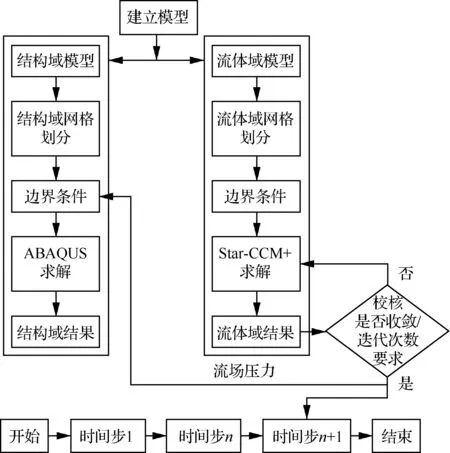
图2 单向流固耦合方法Fig.2 One-way fluid-structure interaction method

1.3 气液两相模型

本文采用VOF多相流模型模拟飞机油箱内的气液两相分布，VOF模型可用于处理含自由液面的问题，通过引入流体各时刻在控制体内的体积分数α来构造和追踪自由液面。若某一时刻流体在控制体内的体积分数α=1，则表示此控制体内全部为该流体；若α=0，则此控制体内不含该流体，全部为另外的流体所占据；若0<α<1，则此控制体内含有该流体以及另外的流体，在此控制体内存在该流体与另外流体的交界面。

1.4 湍流模型

对流体域的求解采用雷诺平均Navier-Stokes(Reynolds Average Navier-Stokes,RANS)两方程模型中的剪切应力运输(Shear Stress Transport,SST)k-ω湍流模型，SST模型已被广泛应用于航空工业和边界层流动。该模型通过考虑湍流剪切应力对输运过程的影响从而对湍流黏性项进行了修正，且在处理近壁面流动问题上具有良好的适应性，在低y+壁面采用低雷诺数模型来计算边界层流动，在高y+壁面采用壁面函数法求解边界层流动，对y+值位于两者之间的壁面则平滑过渡。

1.5 边界条件

半滚倒转机动示意图如图3所示，飞机先绕纵轴滚转180°，然后做向下的半筋斗动作，在垂直面内绕横轴改变俯仰角180°，返回到平飞状态。在计算飞机空间机动轨迹时，假设飞行中无侧滑，发动机推力沿飞行速度方向，并考虑飞机在竖直面内作匀速圆周运动，忽略9g大过载下重力作用对速率的变化，故有

(1)

式中：n为过载系数；F为升力；G为重力；g为重力加速度；a为向心加速度;V为速度;R为倒转半径。

图3 半滚倒转机动示意图Fig.3 Schematic of Split-S maneuver

1.6 计算方法验证

本文建立ABAQUS与Star-CCM+联合仿真单向流固耦合计算方法，通过流场压力的单向传递进行结构响应的求解，采用Souto-Iglesias等[19-20]所开展的矩形液舱晃动实验验证本文所述数值方法的有效性。实验中，矩形液舱绕底面中轴作正弦周期晃动，角位移θ=θmaxsin 2πft(f=1/T)，f为频率，T为周期。液舱尺寸为900 mm×580 mm×50 mm (长×高×宽)，充液高度93 mm，液舱内介质为水和空气。本文选择晃动幅度θmax=4°，晃动周期T=1.92 s工况进行模拟，计算5个晃动周期，结构域壁面视为刚性，液舱模型如图5所示。

图6为液舱左壁第1次冲击过后出现的波浪行进形态，由图6可见模拟与实验得到的行进波形态极为相似。对于两相流晃动问题，轻相对晃动形态的影响尤为显著[21]，因模拟所采用的空气属性与实验现场难以一致，且可能由于实验拍摄角度问题，模拟结果与实验现象在波浪前端存在细微差异。

图7为液舱左壁初始液位处的动态压力模拟结果与实验结果对比，图中p为压力，由图可见模拟结果与试验结果吻合良好。由于液体冲击压力与冲击前波浪形态密切相关且在冲击过程中表现出随机性[22]，压力峰值存在较小误差，最大误差不超过0.5 kPa，所有峰值平均相对误差不超过10%，除峰值以外，曲线其他部位相对误差不超过5%。

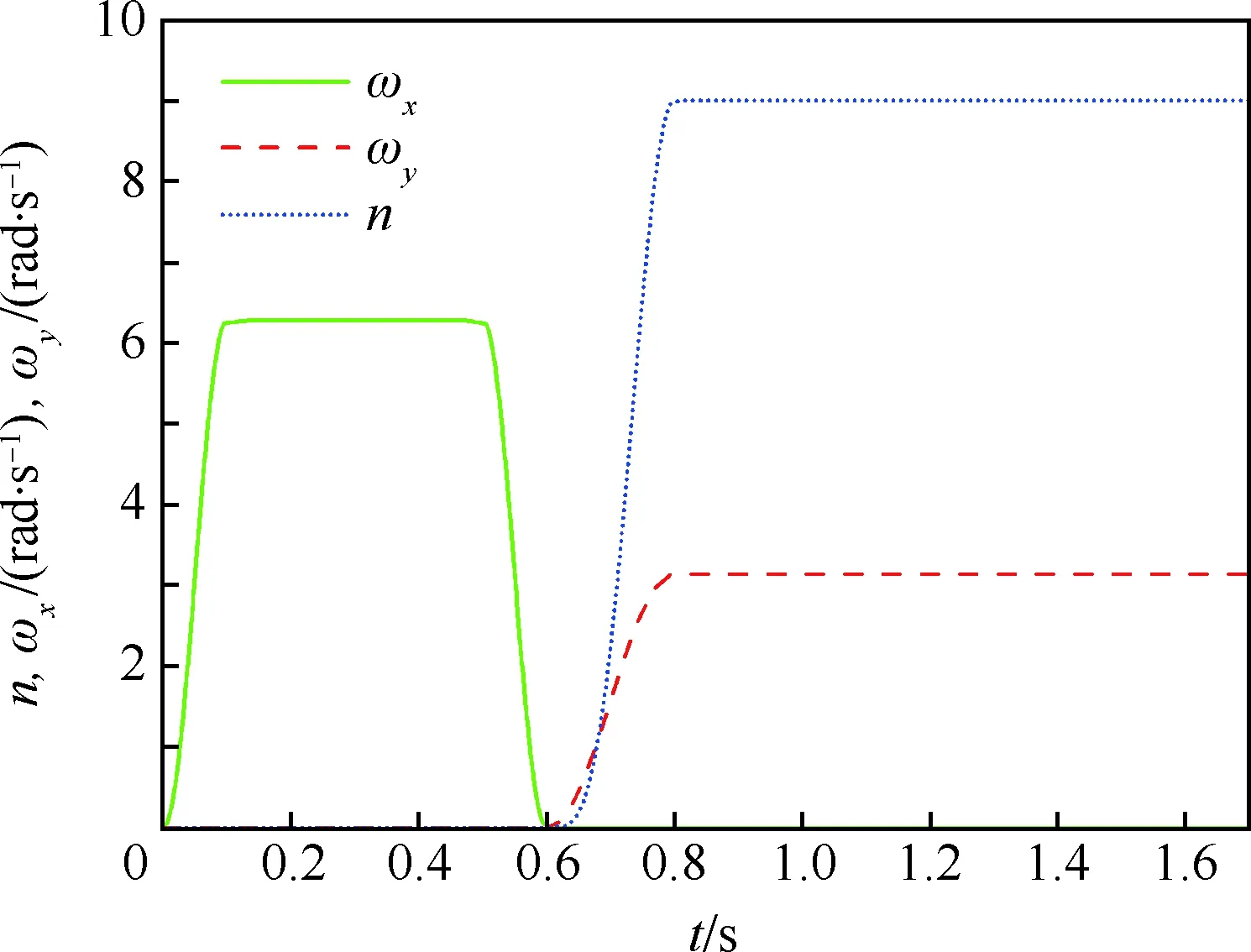
图4 角速度及过载系数变化曲线Fig.4 Curves of anger velocities and overload coefficient

图5 液舱模型Fig.5 Model of tank

图6 波浪行进形态(Δt=0.04 s)Fig.6 Pattern of wave travel (Δt=0.04 s)

图8为结构域与流体域的液舱左壁受力曲线，图中F为压力，由图8可知结构域左壁与流体域左壁受力相近，由于结构域与流体域网格的差异，在数据传递过程中存在插值误差，且结构域受晃动惯性影响，导致图8中两曲线存在较小偏差，但在曲线峰值和变化趋势上保持了良好的一致性，故可认为压力已进行准确传递。

经本节分析，采用ABAQUS与Star-CCM+联合仿真单向流固耦合计算方法对矩形液舱晃动实验进行模拟，Star-CCM+能够精确求解液体晃动特征，且能够准确传递流场压力于ABAQUS进行结构响应计算，说明本方法可有效用于研究飞机油箱晃动的流固耦合效应。

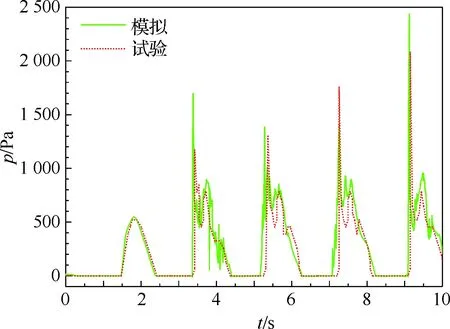
图7 动态压力曲线Fig.7 Curves of dynamic pressures

图8 液舱左壁面受力曲线Fig.8 Curves of force on the left wall of tank

1.7 网格无关性验证

采用单向流固耦合方法分析油液晃动对油箱结构的影响以及内部燃油晃动特性，数据传递是单向的，重点在于流体域的求解。不考虑晃动对固体域的影响，流体域采用切割体网格进行划分，对边角进行加密，共划分6套网格，网格数量分别为63 791、116 842、221 500、317 172、463 559、686 759，分析流体域求解结果对网格的依赖性。6种网格方案如图9所示。

图10为油箱壁面标识，图11为油箱主要受冲击壁面的流体作用力最大值Fmax在不同网格数量下的对比。图12为不同网格数量下流体域最大压力pmax的变化，表4为不同网格数量下pmax和Fmax的值及其出现时刻t*。结合图11、图12和表4可知，当网格数量大于30万时，各壁面Fmax和pmax出现时刻及数值均趋于稳定，pmax数值变化量小于0.5%。选取pmax稳定时刻附近(0.2 s)的燃油晃动形态进行对比如图13所示，网格数量小于30万时，流场形态极不稳定，网格数量大于30万时，流场形态较为稳定，网格数达到40万以上时，流场形态稳定。图14为t=0.2 s时不同网格下的流体域压力场，可见网格数大于30万时，压力场稳定。

图9 网格示意图Fig.9 Diagrams of mesh

图10 油箱壁面标识Fig.10 Marks of tank wall

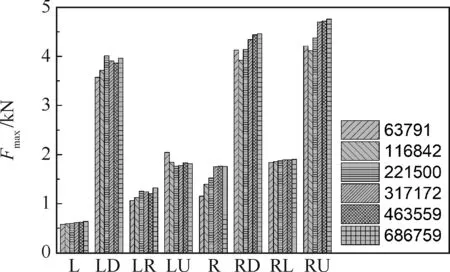
图11 壁面作用力Fig.11 Force on tank wall

图12 流场最大压力Fig.12 Max pressure of fluid

经分析，当网格数量大于30万时，求解结果趋于稳定，增加网格数量对结果影响不大，但对晃动形态的描述不够稳定，网格数量大于40万时，晃动形态稳定，故本文选择的流体域网格数量为463 559。

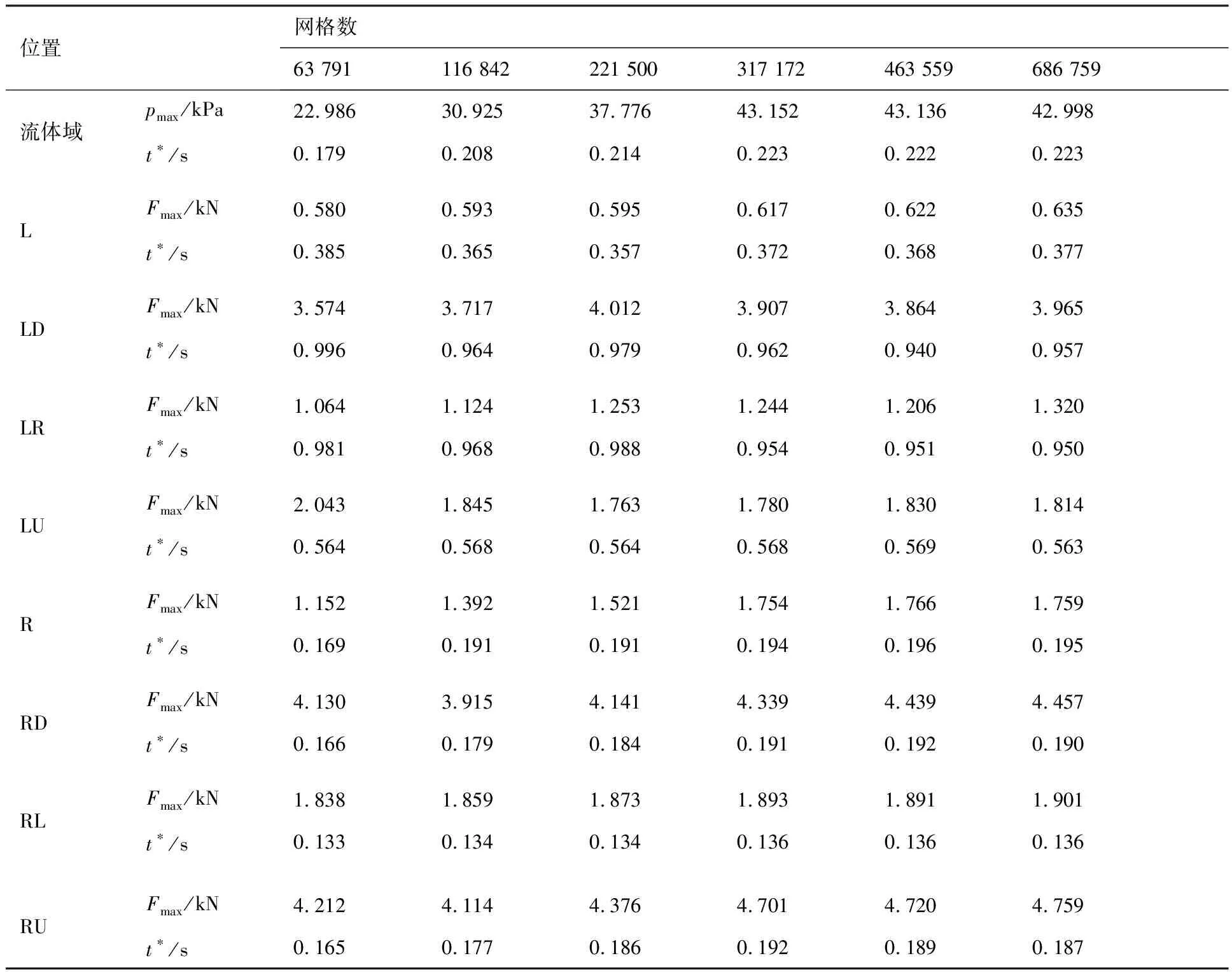
表4 不同网格数量下pmax和Fmax的值及出现时刻t*Table 4 Results pmax、Fmax and t* of fluid of different meshes

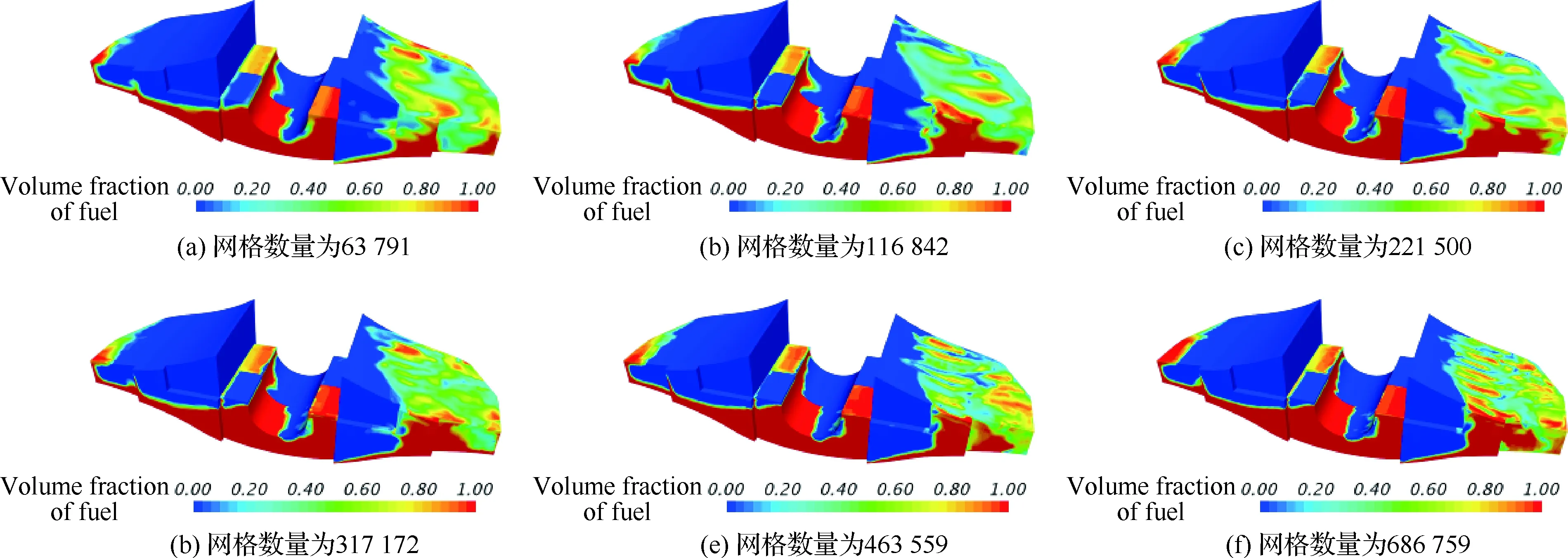
图13 燃油晃动形态(t=0.2 s)Fig.13 Sloshing shapes of fuel (t=0.2 s)

图14 流体域压力场(t=0.2 s)Fig.14 Pressure fields of fluid (t=0.2 s)

2 半滚倒转油箱晃动数值模拟及分析

采用单向流固耦合方法对飞机半滚倒转机动过程中的油箱晃动流固耦合效应进行数值分析，充液率K=0.5，流体域网格数量为463 559，采用VOF多相流模型处理气液两相，湍流模型选择SSTk-ω模型，结构域采用壳单元划分，蒙皮与框架通过连接单元进行连接，并对连接部位进行加密，单元数量为55 124个，耦合时间步长为0.000 5 s，共计算1.7 s。图15为整体油箱结构域网格划分。

图15 整体油箱结构域网格Fig.15 Mesh topology of fuel tank structure

2.1 流体域与结构域结果分析

半滚倒转机动行为分为半滚阶段(0～0.6 s)和倒转阶段(0.6～1.7 s)，图16为油箱内燃油晃动形态，根据图16可见：半滚阶段燃油晃动剧烈，在0.2 s左右燃油猛烈冲击上蒙皮，进入倒转阶段后，由于燃油冲击壁面反弹而出现混沌现象，随着倒转进行，在0.9 s之后燃油逐渐稳定于油箱下半部。

流体域压力峰值时程曲线见图17，压力峰值在0.226 s达到最大值43.14 kPa，0.226 s后压力峰值逐渐减小，0.7～0.8 s之间因油箱倒转燃油再次冲击油箱壁面，压力峰值再次上升，0.8 s后冲击减弱，峰值下降，0.9～1.7 s燃油因大过载作用逐渐稳定于油箱下半部，压力峰值随燃油稳定而缓慢上升。

蒙皮受燃油作用力，蒙皮应变峰值及框架应力峰值时程曲线见图18(a)～图18(c)。根据图18(a)可见：半滚阶段，蒙皮受燃油作用力F在0.2 s后达到最大值，0.2～0.5 s呈现波动状态，0.5～0.6 s 迅速下降，下蒙皮由于半滚180°而在0.6 s几乎不与燃油接触，燃油作用力此刻为0。倒转阶段，燃油因大过载作用逐渐稳定于油箱下半部，使得上蒙皮逐渐脱离与燃油的接触，燃油作用力逐渐减小到0；下蒙皮F在0.6～0.8 s因过载迅速增加而急剧上升，在0.8 s由于油箱倒转过程中燃油有冲击现象，F出现波动，波动过后F随着燃油逐渐稳定而缓慢上升，根据下蒙皮受燃油作用力时程曲线可知，过载导致的燃油作用力大于冲击导致的燃油作用力。

根据图18(b)可见：半滚阶段，上、下蒙皮应变峰值εmax均在0.2 s左右最大，倒转阶段上蒙皮应变峰值较为稳定，下蒙皮应变峰值不断上升；整个机动行为过程中，上、下蒙皮应变峰值均在倒转阶段更大。结合图18(a)可知，半滚阶段由于燃油冲击壁面导致应变峰值出现波动；倒转阶段，上蒙皮不受燃油作用力，下蒙皮F因过载显著增大，故可认为倒转阶段应变变化受过载主导。

根据图18(c)可见：框架应力峰值σmax最大值出现在倒转末段，且应力峰值在半滚阶段出现波动，在0.2 s后达到波峰；倒转阶段框架应力峰值不断上升，在0.9～1.1 s之间上升趋势最快，其余阶段上升较为缓慢。结合油箱过载变化情况可知，半滚阶段燃油晃动对框架应力变化占主导作用，倒转阶段过载对框架应力变化起主导作用。

图16 燃油晃动形态(t=0～1.7 s)Fig.16 Sloshing shape of fuel (t=0-1.7 s)

图17 流体域压力峰值时程曲线Fig.17 Time-history curve of fluid’s peak pressure

油箱最大应力云图见图19，由图19可知应力较大部位主要集中于框架两端与蒙皮连接部位。图20为局部坐标系下油箱最大位移云图，相比于蒙皮，框架最大变形量较小，主要变形部位位于与蒙皮连接处，上、下蒙皮最大位移均出现在右侧；局部坐标系下各部件最大位移值及出现时刻,如表5所示，根据最大位移出现时刻可知油箱部件最大位移均因半滚阶段燃油冲击造成。

图18 蒙皮受燃油作用力、蒙皮应变峰值及框架应力峰值时程曲线Fig.18 Time-history curves of force of fuel on skins, peak strain of skins, and peak stress of frame

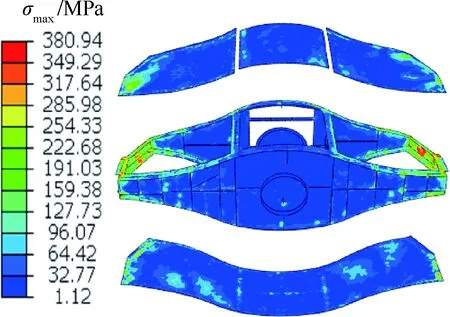
图19 油箱最大应力云图Fig.19 Max stress of fuel tank

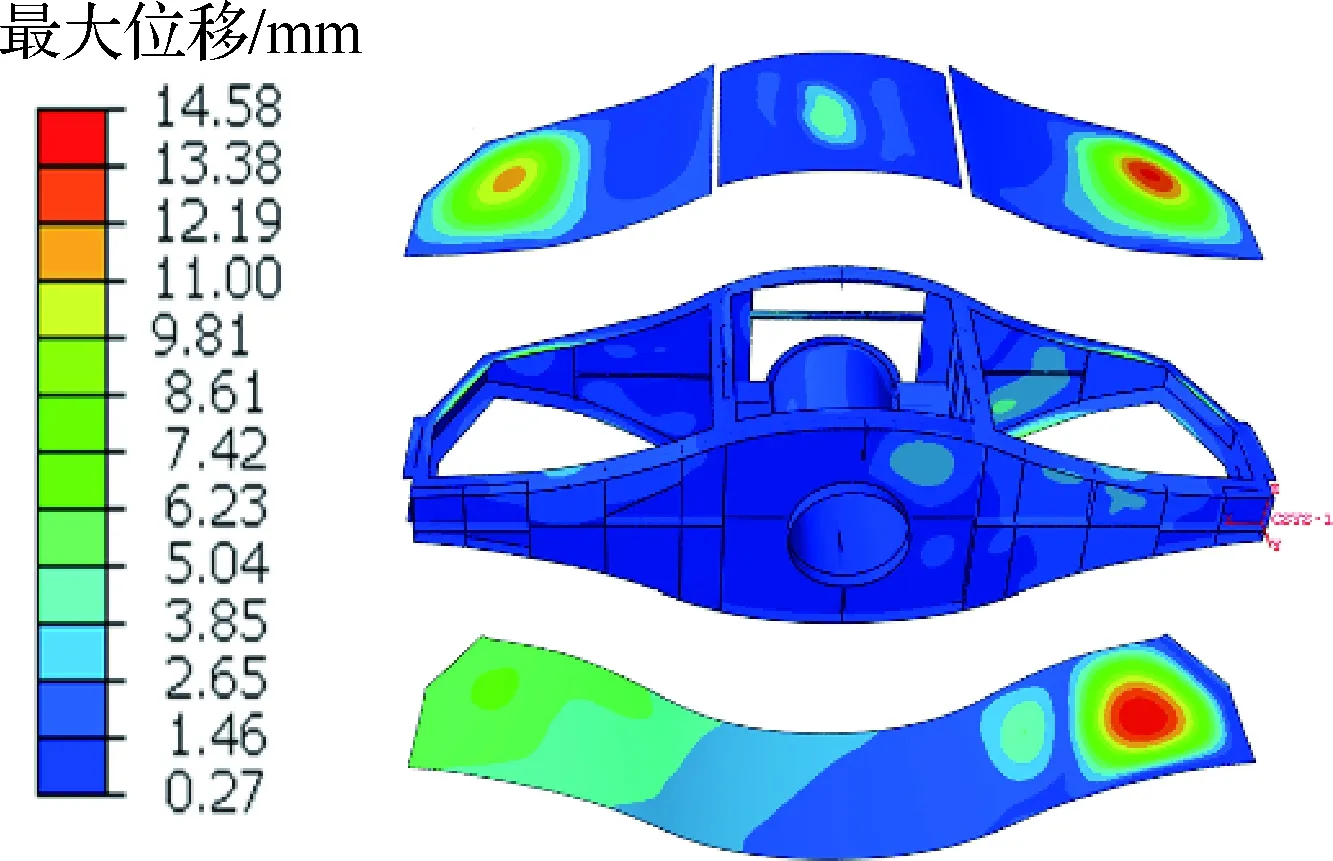
图20 油箱最大位移云图Fig.20 Max displacement nephogram of fuel tank

经验表明当蒙皮与框架连接部位间隙大于0.25 mm时油箱可能发生漏油[23]，通过连接部位连接单元的相对位移可判断油箱是否存在漏油危险。对于本文研究对象，出于保守设计考虑，设定漏油判断标准为0.2 mm。将连接单元分为12个区段，区段标识如图21所示，表6为各区段最大相对位移值，由表6可知各区段最大相对位移均不超过0.2 mm，油箱不发生漏油。

表5油箱部件最大位移(局部坐标系)

Table5Maxdisplacementofcomponentsoftank(Localcoordinatesystem)

部件最大位移/mmt∗/s框架6.780.235上蒙皮13.940.225下蒙皮14.580.190

图21 连接单元区段标识Fig.21 Marks of zones of connector

表6 连接单元相对位移Table 6 Relative displacement of connectors

2.2 不同充液率对油箱晃动的影响

为探究半滚倒转机动过程中充液率K对油箱晃动的影响，分析少油(K=0.3)、半油(K=0.5)、多油(K=0.7)3种不同充液率下的晃动情况。图22为不同K下的流体域压力峰值时程曲线，由图22可知：随着充液率增加，半滚阶段流体域压力峰值最大值出现时刻逐渐提前，倒转阶段压力峰值随着充液率增加而增加；半油状态pmax大于少油与多油状态。不同K下pmax时刻燃油晃动形态及流体域压力场见图23，由图23可知：少油与半油状态，破碎波与壁面冲击出现最大压力，冲击影响范围小；多油状态，驻波冲击壁面产生最大压力，冲击影响范围较大。

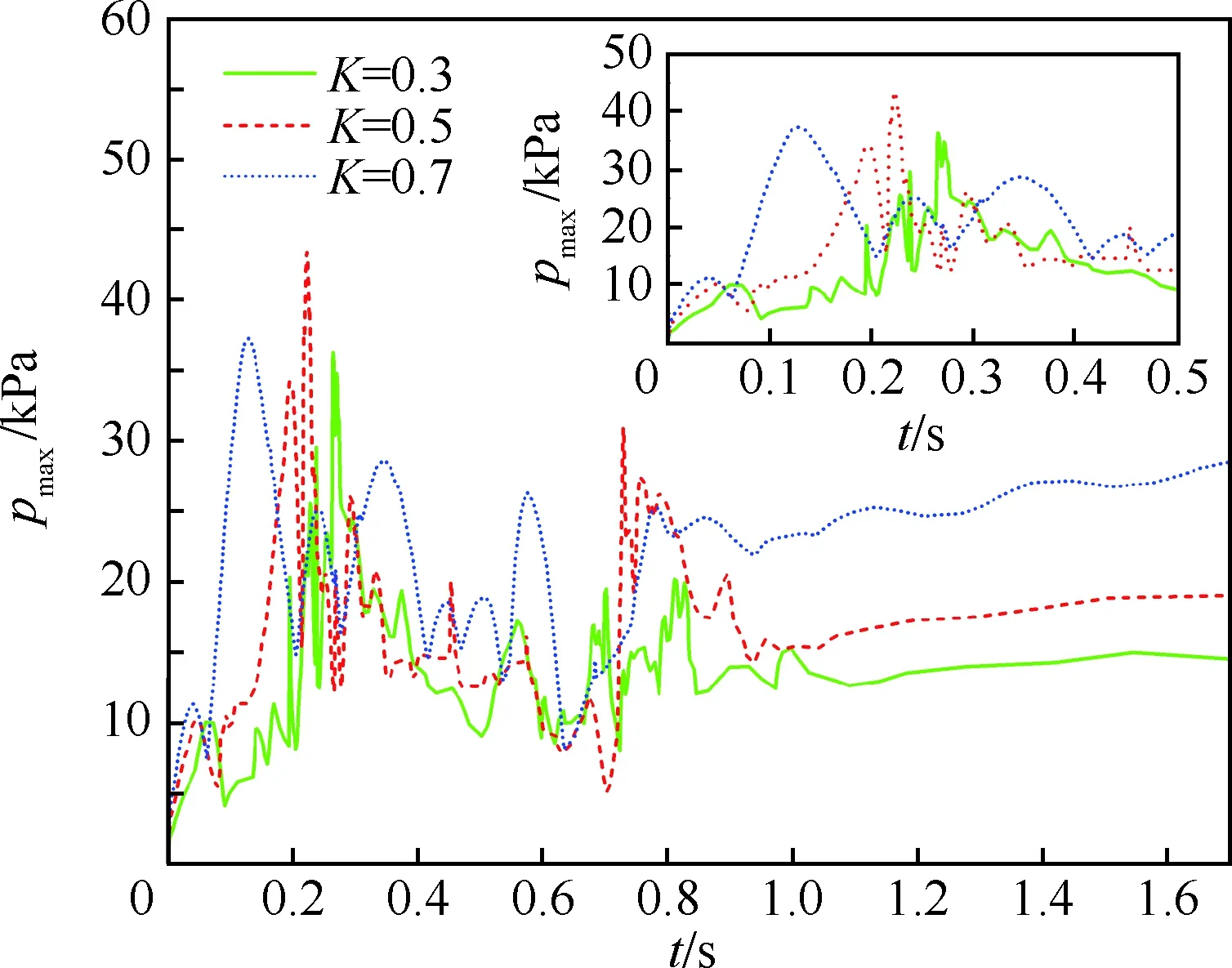
图22 不同K下的流体域压力峰值时程曲线Fig.22 Time-history curves of fluid’s peak pressures with different K

图24为不同K下的蒙皮受燃油作用力时程曲线，由图24可知：F随着充液率增加而增加，在0.6 s后均因油箱半滚180°导致下蒙皮短暂脱离与燃油的接触而作用力为0；倒转过程中燃油在过载作用下脱离上蒙皮，上蒙皮不再承受燃油作用，下蒙皮受燃油作用力因燃油逐渐稳定于油箱下半部而增大，且随着充液率增加，F增加趋势加快，这说明充液率越大倒转过程中燃油晃动越不易稳定。

图25为不同K下的部件最大应力，由图25可见：部件最大应力在半滚阶段和倒转阶段随充液率变化呈现不同规律。半滚阶段，各部件最大应力均与充液率正相关；倒转阶段，上蒙皮最大应力几乎不变，下蒙皮与框架最大应力随充液率增加而增加，但下蒙皮最大应力增加明显，框架最大应力增幅不大，这是因为倒转阶段燃油作用力主要作用于下蒙皮导致。