非均匀加热管内单相流动传热特性数值模拟
2019-03-28,,
, ,
(中国船舶重工集团有限公司第七○三研究所,哈尔滨 150078)
0 引 言
管路内单相流体的流动与传热现象在动力、化工、核能、制冷、石油及航天等现代工业中广泛存在。例如,火电站和核电站中的各种热交换器,化学工程和制冷设备中的各式蒸发器和冷凝器,以及宇航工业中的火箭推进系统等等。这些动力系统或设备的运行状况都与流动和传热过程有关,其优化设计、经济技术指标的提高以及安全性的保障,客观上要求准确掌握相关的流动和传热方面的各种知识[1]。前人也对均匀加热管内流动与传热特性进行了深入研究,发展了一系列的传热系数及压降的关联式[2-3],为实际工程应用提供了理论依据。
在某些特殊场合,管路受热是不均匀的,如电厂中的锅炉水冷壁、核反应堆的管式换热器、太阳能发电系统熔盐吸热器等,均是一侧受热,而另一侧绝热。杨敏林[4]数值计算了半周加热熔盐吸热管在高温、高热流密度条件下的管内流速和温度分布规律及其换热特性,为塔式太阳能热发电熔盐吸热器的设计和运行提供重要依据。胡志宏[5]采用半周镀银方法,试验研究了超临界及近临界区垂直及倾斜圆管内传热特性及临界热负荷特性。Lekakh[6]研究了半周加热对管内压降的影响,认为管外非均匀加热对管内压降影响不大。Dedov[7]研究了半周加热管内单相流体换热特性,认为非均匀加热管内的平均换热系数依然可以采用Dittus-Boelter公式。另外Boscary[8]、Olekhnovitch[9]、Ami[10]几位学者对低压、大热流密度下半周加热管内的临界热负荷特性开展了研究,给出了相应的临界热负荷预测关联式。然而,对于中高压情况下流体流速、壁厚、温度对半周加热管内的热流量分配及单相换热特性和摩擦压降特性的影响规律目前还没有文献报道。
由于半周加热的实现方式比较困难,而且通过实验的方法很难确定流体在管内的具体流动情况,加上实验的方法在经济性和安全性等方面存在一些问题,所以数值模拟作为一种实验研究的替代方法获得了广泛的应用。文中利用计算流体力学的方法,对不同热流密度、不同管内工质流速、不同壁厚时壁温分布及加热侧与绝热侧的热流量比值进行了计算,分析了热负荷非均匀分布对管内换热系数及压降的影响,为圆管换热器设计和运行提供理论依据。
1 数理模型及数值方法
1.1 控制方程
采用Fluent软件进行数值模拟时,对管内流动做如下假设:
(1)管壁加热侧热流密度恒定且均匀;
(2)流动为稳态流动;
(3)管内为强制对流。
流场的控制方程为:
(1)连续方程:
(2)动量方程:
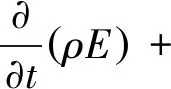
(3)能量方程:

1.2 物理模型
为模拟半周加热对壁面及管内流体温度分布的影响,我们建立了如下传热模型,如图1所示。模型半周接受恒定且均匀的热流密度,另外半周处于绝热状态。加热侧热流密度范围为600~2 000 kW/m2。过冷水由管道入口流入,加热到接近饱和温度时流出管道,其入口压力为10 MPa,入口温度为373 K,入口流速范围为0.5~3 m/s。水在受热管道中的物性随着温度的升高不断变化,其密度(kg/m3)、定压比热(J/kg/K)、运动粘度(kg/m/s)及导热系数(W/m/K)随温度的变化规律为:
管道结构参数包括内径8 mm,外径12~14 mm,壁厚2~3 mm。受热管材料为316不锈钢,其密度为7 930 kg/m3,定压比热为460 J/kg/K,导热系数(W/m/K)随壁面温度不断发生变化:
λ=0.014 886T+14.408

图1 传热模型
1.3 数值方法
管内工质的流动是一个处于紊流状态的三维稳态流动,其换热过程包括热传导及热对流两种形式。因此,数值模拟的计算域为壁厚和流体流过的区域,控制方程为三维流动的连续方程及N-S动量及能量方程,湍流模型k-ε采用标准湍流模型,压力-速度耦合采用Simple算法,对流插值采用QUICK格式。
模型网格采用四面体网格,设置合适的步长,节点数共279 720个。入口为速度入口,出口为OUTFLOW,加热侧为热流边界,绝热侧热流密度为0,内壁面为耦合边界。计算在整个区域进行,迭代次数设为1 000次,经过约400次的迭代计算收敛。
2 结果分析与讨论
2.1 半周加热管道不同位置处的壁温分布情况
对壁厚为3 mm,热流密度为1 000 kW/m2,速度为3 m/s时半周加热管道入口、中间及出口处的温度分布情况进行了计算。
由图2可以看出,从管道入口到出口,流体温度逐渐升高,绝热侧壁面温度也随之升高,两侧壁温不均匀程度降低。这是由于随着流体温度升高,对流换热温差变小,加热侧通过对流换热作用进入流体的热量逐渐减少,而通过导热作用传导到绝热侧的热量越来越多,因此两侧不均匀程度逐渐降低。
2.2 热流量比值的影响规律
对壁厚为3 mm,热流密度为1 000、2 000 kW/m2,速度为1、2、3 m/s时管道出口处的温度分布情况及两侧平均热流量比值进行了计算。
由图3可以看出,热流密度一定时,流速越高不均匀度越高。这是因为管内流速越高,管内对流换热效果越强,加热侧的热量主要通过对流换热进入管内流体,向绝热侧导热量则相对减小,因此流速越高,两侧热流量比值越高。当热流密度增加一倍时,随着流速的变化两侧热流量比值变化趋势相同。速度相同时,两侧热流量比值随热流密度的升高稍有增加,这是因为热流密度越高,加热侧壁温越高,壁面导热系数随之稍有增大,因此热量从加热侧进入流体的比例增大。
对壁厚为2 mm,热流密度为1 000 kW/m2、2 000 kW/m2,速度为1、2、3 m/s时管道出口处的温度分布情况及两侧平均热流量比值进行了计算。

图2 半周加热管道不同位置处的壁温分布情况

图3 热量密度及速度对壁面温度分布及热流量比值的影响(左:壁厚3 mm,右:壁厚2 mm)
与壁厚为3 mm时相同,热流量比值随管内工质流速增加而增加,而热流密度对热流量比值的影响则不大。
将上述几种工况下两侧热流量比值整理列入表1。由表1可以看出,壁厚为2 mm比壁厚为3 mm时不均匀程度增强。这是由于壁厚值越小,加热侧由外壁面进入流体的总热阻越小,热量主要通过加热侧进入工质,通过导热进入绝热侧的热量减小,两侧热流量比值增加。从表1还可以看出,流速越大,壁厚对热流量比值的影响越明显。这是因为主要热阻在于壁面导热,流速越大,管内对流换热热阻越小,导热热阻对整个换热的影响越显著。因此流速越大,改变壁面热阻对壁面两侧热流量比值的影响越明显。
下面将以符号ψ表示平均热流量比值。取下面参数范围内两侧壁面热流量比值的平均值,以方便对传热系数进行修正:壁厚为2 mm时,ψ=5.2,壁厚为3 mm时,ψ=4。

表1单相液体区不同壁厚加热侧与绝热侧热流量比值
2.3 均匀加热管内换热特性及摩擦压降特性
对管径φ14*3 mm的均匀加热管内的换热系数与压降进行数值模拟,入口流速范围为0.5~2.5 m/s,热流密度为600~2 000 kW/m2,具体参数设置如表2所示。数值模拟结果与经典的传热系数公式和摩擦压降系数公式进行对比,对比结果如图4-5所示。
Dittus-Boelter传热系数计算公式:
摩擦压降计算公式:
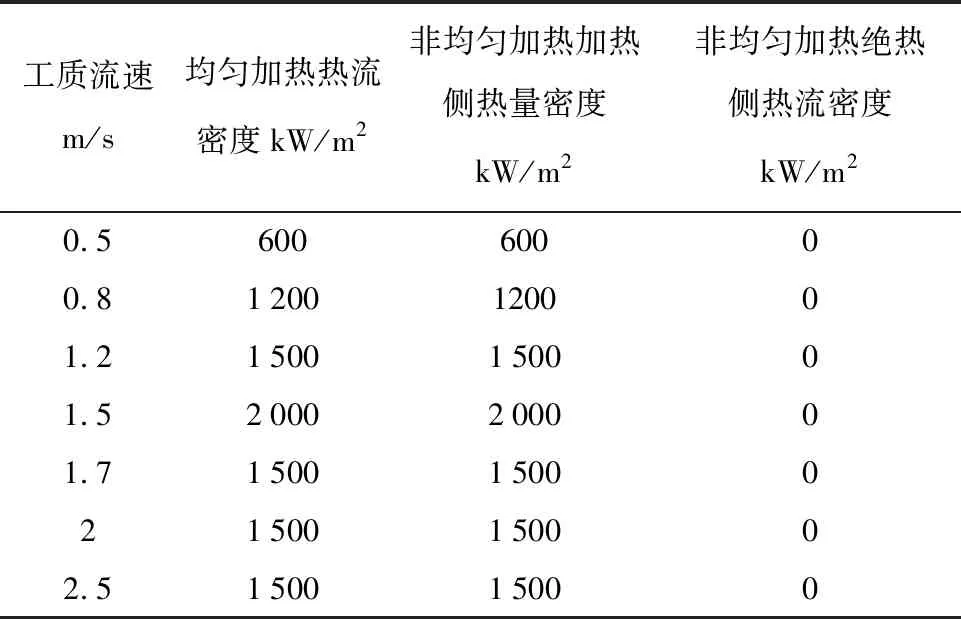
表2数值模拟流体参数表
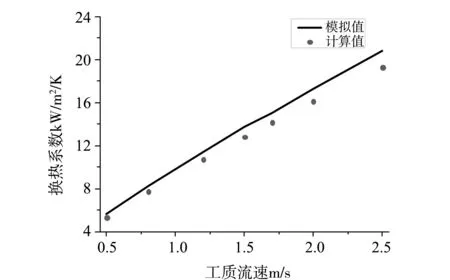
图4 均匀加热管内换热特性
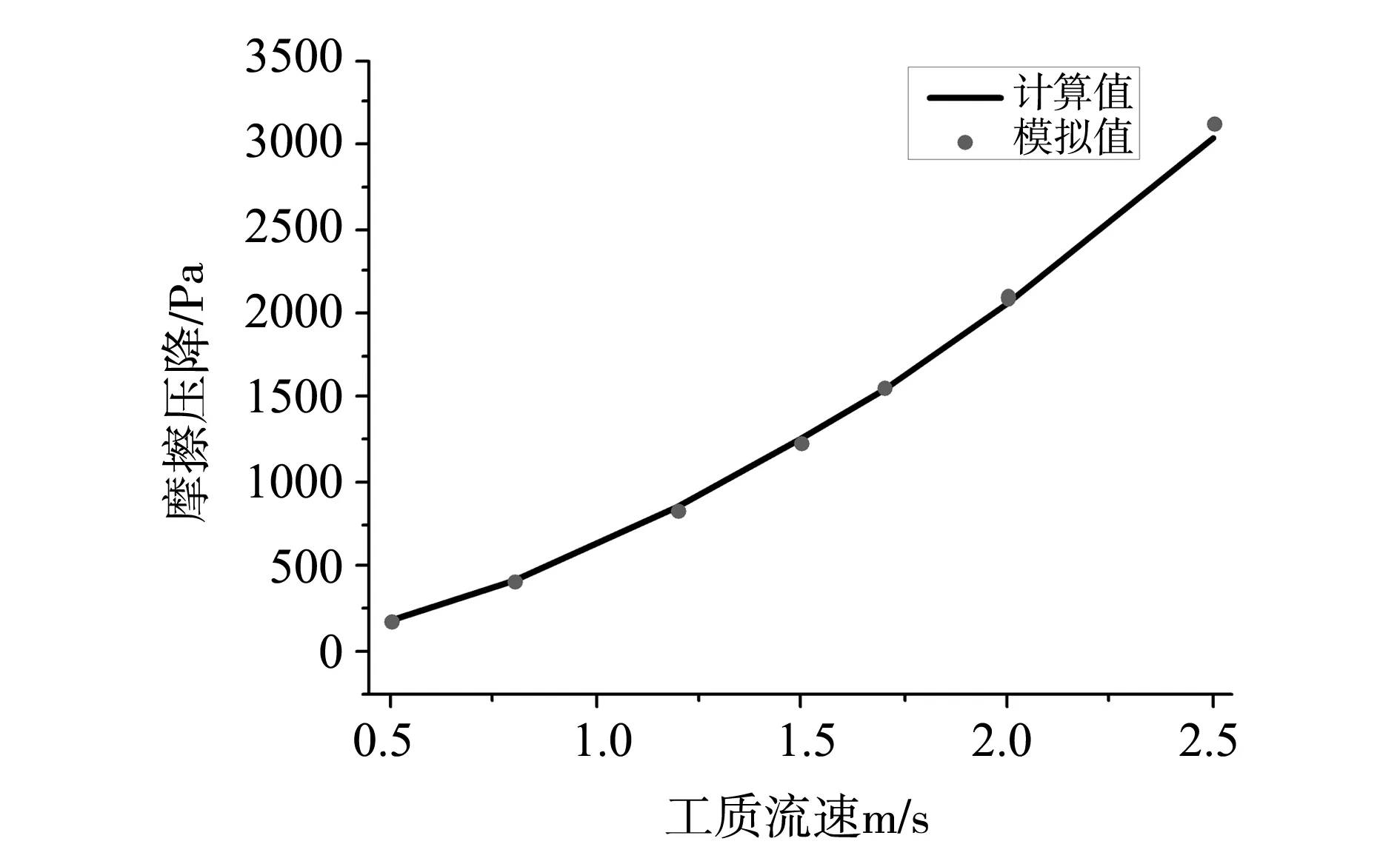
图5 均匀加热管内摩擦压降特性
由图4-5可以看出,数值模拟结果与经验关联式预测结果基本一致,摩擦压降和换热系数模拟值与计算值最大误差分别为2.8%和7.38%,说明所采用的数值方法是正确的。
2.4 非均匀加热管内换热特性及摩擦压降特性
为与均匀加热管内的换热特性和摩擦阻力特性进行对比,采用相同的圆管尺寸φ14*3 mm,相同的入口流速0.5~2.5 m/s,加热侧热流密度同样为600~2 000 kW/m2,绝热侧热流密度为0。具体的参数设置如表2所示。将非均匀加热管内平均换热系数和摩擦压降与均匀加热时的模拟值进行对比。对比结果如图6-7所示。非均匀加热管内平均换热系数和摩擦压降与均匀加热时相比最大偏差分别为7.68%和4.8%,说明在所计算的参数范围内,管外热负荷非均匀分布对管内单相流的平均换热系数和摩擦压降影响不大,可以采用均匀加热管内的相应计算关联式进行预测。这与Lekakh[6]和Dedov[7]的研究结论一致。

图7 非均匀加热管内摩擦压降特性

图6 非均匀加热管内换热特性
对加热侧和绝热侧的换热系数进行了对比计算,对比结果如图8所示。由图8可以看出加热侧和绝热侧换热系数差别较大,绝热侧换热系数比加热侧换热系数大,而且工质流速越大,管内换热越好,两者差别越大。
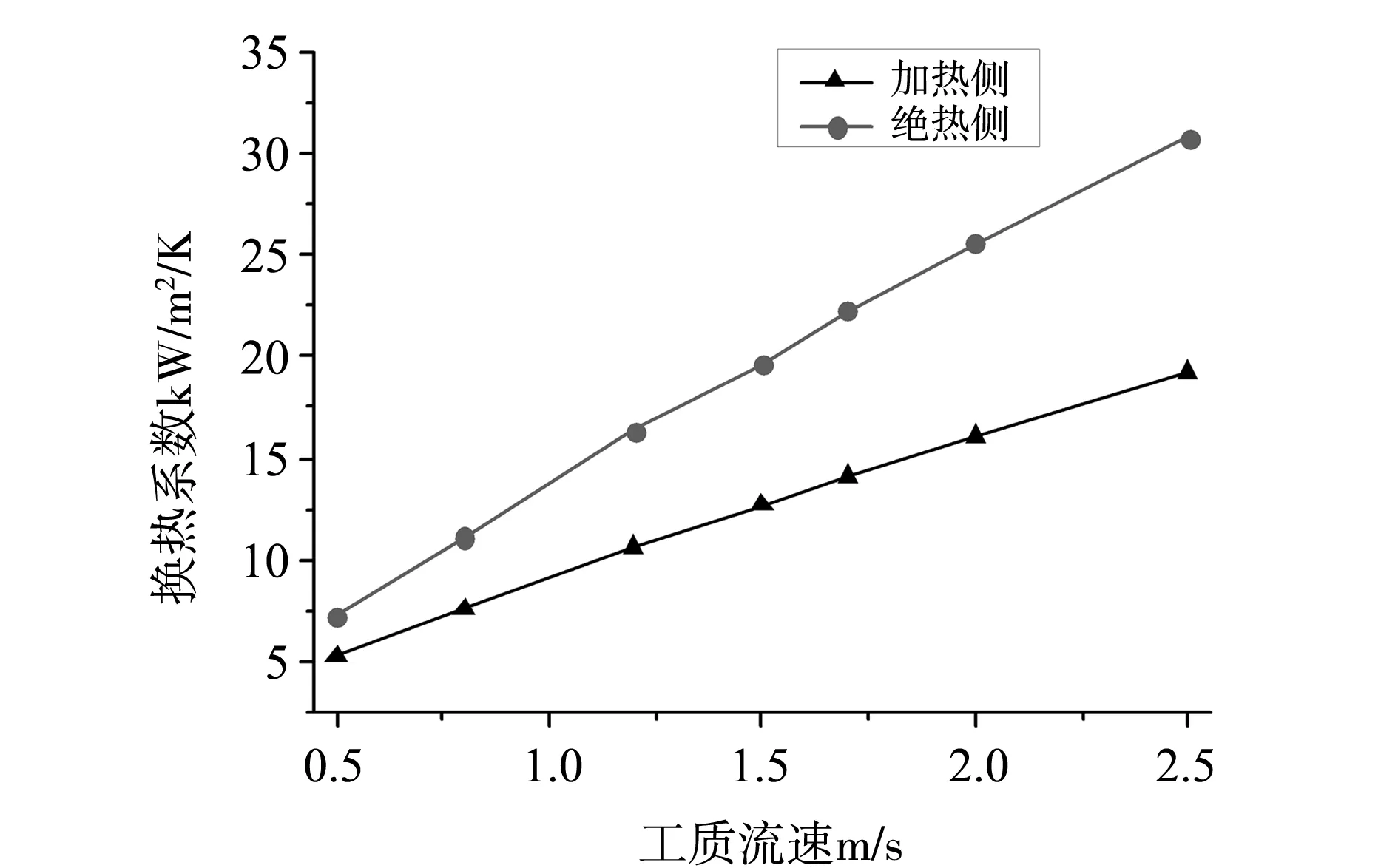
图8 加热侧与绝热侧换热系数对比
3 结束语
针对螺旋管半周加热的特点,在课题研究的参数范围下,采用FLUENT对半周加热在不同热流密度、不同管内工质流速不同壁厚的壁温分布及加热侧与绝热侧的热流量比值进行了计算。结果表明:热流密度一定时,管内工质流速越高,两侧热流量比值越大,不均匀程度越强;管内工质流速相同时,热流密度对不均度的影响不是很大。壁厚越小,两侧不均匀度越大。
分析了非均匀加热对管内换热特性和摩擦阻力特性的影响,对比结果表明管外热负荷非均匀分布对管内单相流的平均换热系数和摩擦压降影响不大,可以采用均匀加热管内的相应计算关联式进行预测。加热侧和绝热侧换热系数差别较大,绝热侧换热系数比加热侧换热系数大,而且工质流速越大,管内换热越好,两者差别越大。
