谈谈数学教学中的“微课效应”

☉江苏省南京市第十二中学 仇清钟

什么是微课？微课是以短小精悍的视频为主要载体，以新课程标准、教学目标所提出的要求作为根据的一种教学手段.在微课的设计中，教师可以灵活地对相关教学资源进行合理整合.微课的时间虽然很短，但教学效果不容小觑，它渐渐改变了当前的教学模式，让教学更人性化，更切合学生的认知水平.那么，微课能给我们的课堂教学带来哪些变化呢？笔者结合高中数学教学的实践活动谈谈以下几点感受.

微课效应一：激发学生的学习兴趣

在高中课程中，数学一向被认为是最难学的学科之一.严谨抽象、灵活多变、计算烦琐、匪夷所思等几乎成了数学这门课的“属性”，于是，学生对数学这门学科似乎有一种天生的恐惧感.如何让学生消除恐惧感，亲近数学，热爱数学呢？此时微课可以起到不小的作用.常言道，兴趣是最好的老师.如何让学生对数学产生兴趣，是教师的责任所在.实践证明，教师的说教于事无补，而设计贴近学生认知的微课，却往往能扭转乾坤.

良好的开端是成功的一半.对于高一新生来说，培养他们学习数学的兴趣比什么都重要.集合是高中数学大厦的基石，也是高一新生接触的高中的第一个数学知识点，虽然难度不大，但体现了高中数学的许多特点，如思维的严谨性（元素的互异性、空集等问题），以及数学思想的应用性（方程思想、数形结合思想、分类讨论思想等），因此，对于集合这一章节的内容，学生必须牢固掌握.为了培养学生的学习兴趣，笔者设计了如下微课视频：

在蓝天白云下，几十只燕子呈人字形排列，展翅飞翔；

在茫茫的大草原上，几匹野马伴随着声声马蹄，飞驰而来；

在蔚蓝的大海上，一群海豚，逐浪翻滚，泛起浪花朵朵；

在一所中学操场的草坪上，几个男生在踢足球，耳边传来阵阵“加油，加油”的声音.

这时，银幕上传来了雄浑有力的声音：

“同学们，集合是什么？集合就是几十只燕子，集合就是几匹野马，集合就是一群海豚，集合就是正在踢足球的男生，集合就是我们班，我们班就是一个集合.我们班里的每一个学生都是这个集合中的元素，我们的地位平等，和睦相处，即元素的无序性；我就是我，班里只有一个我，即元素的互异性；我们班里有40位同学，缺一不可，人数与人员已定，即元素的确定性.”

几段优美的画面截屏，一段借境发挥的解说，用时不到5分钟，却把学生带入了一个充满画面感的情景.让学生从中感知到什么是集合，并理解了集合元素的三大特性，即元素的无序性、互异性与确定性.与此同时，也让学生初次感到高中数学其实并不难，而且十分有趣，于是增强了他们学好数学的自信心.

常言道：先入为主.新授课的引言是微课教学的良好契机.教师还可以在微课中加入历史故事、趣味问题、社会现象等数学文化元素，让学生带着好奇，带着疑问，满怀兴趣地走进即将学习的新课内容.

微课效应二：优化教师的教学活动

好的微课设计，可以使目标更明确，重点更突出，思路更清晰.微课中，凝聚着课堂教学的精华，利用微课教学，可以尽可能地提高课堂教学的有效性.由于微课可以重复使用，这也减少了教师的工作量.当学生一遍没有学懂的时候，可以再学一遍.正是由于微课的应用具有灵活性，能够优化教学活动，所以才受到广大教师的认可与推广.微课短小精悍，可以帮助教师围绕教学的重、难点展开教学，分散重点，突破难点，使学生更容易接受，能够减轻学生的学习负担，体现教学的艺术性和学生学习的探究性与合作性.

例如，在高三复习课上，笔者设计了一个“与线性规划交汇的几何概型变式探究”的微课：

求解与面积有关的几何概型时，关键是要弄清某事件对应的几何元素，必要时可根据题意构造两个变量，把变量看成点的坐标，找到全部试验结果构成的平面图形，以便求解.尤其是一类与线性规划交汇的几何概型，值得关注.

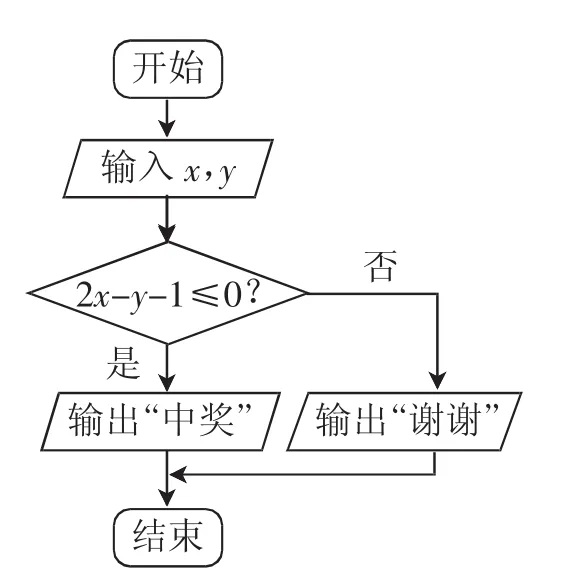
图1

变式探究1：某商场十一期间进行抽奖活动，规则是：顾客通过操作按键使电脑自动产生两个［0，1］之间的均匀随机数x，y，并按如图1所示的程序框图执行.若电脑显示“中奖”，则代表中奖；若电脑显示“谢谢”，则不中奖.求该顾客中奖的概率.

变式探究2：甲、乙两人约定在6时到7时之间在某处会面，并约定先到者应等候另一个人一刻钟，过时即可离去，求两人能会面的概率.

变式探究3：在区间［0，2］上任取两个实数a，b，求函数f（x）=x3+ax-b在区间［-1，1］上有且仅有一个零点的概率.

探究发现：与线性规划交汇的几何概型，关键是要找到表示基本事件的不等式组和构成事件A发生的不等式组，并将不等式组图形化，然后分别算出它们的面积Ω与Ω1，于是所求概率

微课的诞生，是为了让学生的学习更便利、更有效，充分利用课堂的每一分钟，让教师的教学活动更加优化.从上面这段微课设计可以看出，一个微课，对于高三复习来说，就是一个知识点，一个考点，若没有微课，教师可能要反复强调，而一个微课却让学生一目了然，而且能帮助学生全面掌握复习的重点与难点，掌握基本的解题技巧与方法.

微课效应三：促使个别化教学更有效

大家知道，高中数学能否学好，勤奋固然重要，但天赋也不可或缺.由于学生对数学的认知水平参差不齐，班级里出现数学后进生和数学尖子生在所难免，如何有效地转化数学后进生和进一步拔高数学尖子生呢？微课可以起到非常大的作用，它可以帮助教师有效开展个别化教学.

例如，对于数学后进生，教师可以设计有关错题的微课，帮助学生纠错，在“解三角形”这一章学习中，笔者设计了以易错点为主要形式的微课帮助学生纠错，具体如下：

易错点1：利用正弦定理求三角形的内角时丢解.

友情提示：在利用正弦定理求角时，由于正弦函数在（0，π）内不严格单调，所以角的个数可以不唯一，这时应注意借助已知条件加以检验，务必做到不漏解、不多解.

易错点2：忽视三角形的内角和定理.

友情提示：在解三角形问题时，应注意A+B+C=180°，且A＞0°，B＞0°，C＞0°.

易错点3：忽视三角形的三边关系.

例3 设2a+1，a，2a-1为钝角三角形的三边，求实数a的取值范围.

友情提示：在求有关参数取值范围时，不可忽略三角形三边固有的关系，否则会使某些字母的取值范围变大.

易错点4：忽视题设中的隐含条件.

例4 在△ABC中，已知∠A＞∠B＞∠C，且∠A=2∠C，b=4，a+c=8，求a，c的长.

友情提示：在解三角形边长问题时，由∠A=2∠C，应注意∠C为锐角，从而做到不多解、不漏解.

易错点5：等式变形时随意约去公因式.

例5 在△ABC中，若（a-ccosB）sinB=（b-ccosA）·sinA，判断△ABC的形状.

友情提示：解决此类问题的基本方法是将已知的边角关系式化为一边为0，另一边为三角式的乘积形式或平方和形式，或另一边为关于三边的多项式.注意不能随意约去公因式，否则结论便不完整了.

这个微课通过例题和友情提示，帮助数学后进生找到错误原因，从而达到防患于未然的效果.

实践证明，高中数学微课教学模式正在悄悄地改变我们的教学模式与教学理念，其为高中数学教学注入了新的活力.我们相信，只要大家重视微课这个“新生事物”，它必将在数学教学中发挥越来越大的作用.W