活跃在全国各地模拟卷中的创新型函数
2019-03-28湖北省襄阳市第一中学
☉湖北省襄阳市第一中学 王 勇
函数是中学数学的主要内容,也是历年高考“经久不衰”的重点、难点和热点内容.高考命题者为了命制好函数题而绞尽脑汁、挖苦心思,所命制的函数题超凡脱俗、新颖别致,颇具思考性和挑战性.一些构思精巧、魅力四射的创新型函数频频“闪亮登场”,这些创新型函数是考查学生的迁移能力、探究能力及核心素养的极好素材,具有很好的区分与选拔功能.下面从全国各地模拟卷中精选几类创新型函数并结合典型例题加以剖析,旨在探索题型规律,揭示解题方法.
一、n阶整点函数
例1 (2018年深圳市模拟题)在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,若函数f(x)的图像恰好经过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.给出下列函数:
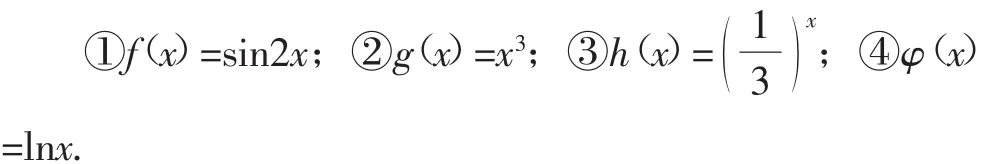
其中是一阶整点函数的是( ).
A.①②③④ B.①③④ C.①④ D.④
解析:对于函数f(x)=sin2x,它的图像(图略)只经过一个整点(0,0),所以它是一阶整点函数;
对于函数g(x)=x3,它的图像(图略)经过整点(0,0),(1,1),…,所以它不是一阶整点函数;
对于函数φ(x)=lnx,它的图像(图略)只经过一个整点(1,0),所以它是一阶整点函数.
综上,本题应选答案C.
点评:根据新定义的一阶整点函数的含义,对四个函数一一进行分析,判断它们的图像是否恰好经过一个整点,即可得出正确的选项.
二、同形函数
例2(2018年衡阳市模拟题)若两个函数的图像经过若干次平移后能够重合,则称这两个函数为“同形函数”.给出四个函数:f1(x)=2log2x,f2(x)=log2(x+2),f3(x)=(log2x)2,f4(x)=log2(2x),则“同形函数”是().

解析:f4(x)=log2(2x)=1+log2x,将函数f4(x)的图像沿y轴向下平移1个单位长度得到函数y1=log2x的图像,再将此函数的图像沿x轴向左平移2个单位长度得到函数y2=log2(x+2)的图像,即函数f4(x)的图像经过平移后可得到函数f2(x)的图像,故f4(x)与f2(x)是“同形函数”,故选D.
点评:本题给出“同形函数”的定义,重点考查函数的图像变换(平移变换).
三、平均值函数
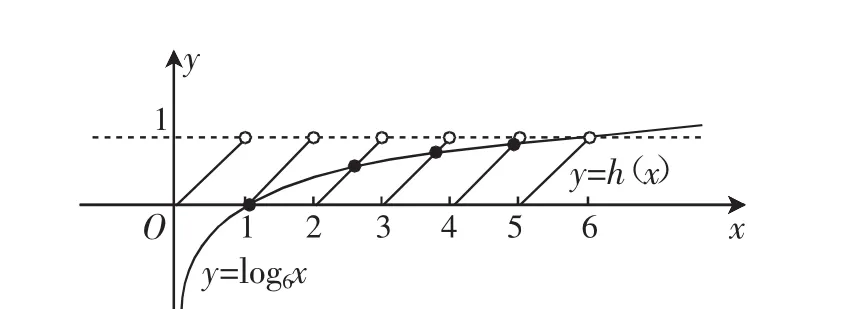
例3(2018年襄阳市模拟题)定义:如果函数y=(fx)在定义域内给定区间[a,b]上存在x(0a 解析:因为函数(fx)=-x2+mx+1是区间[-1,1]上的平均值函数,所以在(-1,1)内有实数根,即关于x的方程x2-mx+m-1=0在(-1,1)内有实数根,解方程得x1=1,x2=m-1,由题意必有-1 点评:根据“平均值函数”的定义,将问题转化为方程x2-mx+m-1=0在(-1,1)内有实数根,而此方程的两实根容易求得,在此基础上列出关于m的不等式即可求解. 例4(2018年宜昌市调考题)函数f(x)=[x]-x([x]表示不超过x的最大整数,如[-3.6]=-4,[2.1]=2),设函数g(x)=f(x)+log6x,则函数y=g(x)的零点的个数为______. 解析:令g(x)=f(x)+log6x=0,得log6x=-f(x),设h(x)=-f(x)=x-[x](x>0)表示的是正实数x的小数部分,则h(x)∈[0,1).分别作出函数y=h(x),y=log6x的图像,如图1所示. 图1 由图1可知函数y=h(x)与函数y=log6x的图像有4个交点,故函数y=g(x)的零点有4个. 点评:本题不仅考查了函数的零点、函数的图像及函数的性质,还考查了数形结合思想.解决本题的关键是准确理解[x]的含义(可以这样理解:设n∈Z,若n≤x ①y=(fx)的值域为R; ②y=(fx)在(0,+∞)上单调递减; ③y=(fx)的图像关于y轴对称; ④y=(fx)的图像与直线y=ax(a≠0)至少有一个交点. 其中,正确结论的序号是______. 综上所述,本题应填③④. 点评:画出“囧函数”的图像,充分利用“囧函数”的图像特征来确定函数的有关性质. 图2 例6(2018年重庆市模拟题)设函数(fx)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意的x∈[a,b],都有|(fx)-g(x)|≤1,则称(fx)与g(x)在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.设函数(fx)=lnx]上是“密切函数”,则实数m的取值范围是( ).四、取整函数(高斯函数)
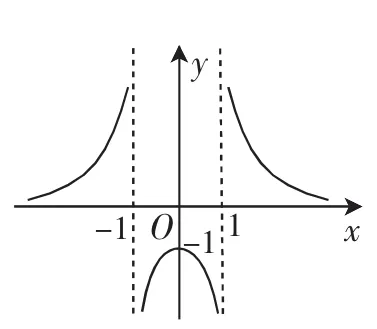
五、囧函数
六、密切函数


