基于时间序列模型的济南趵突泉地下水位预测

张郑贤，刘 艺，张锋贤

（1.济南大学 水利与环境学院/山东省地下水数值模拟与污染控制工程技术研究中心，山东 济南 250022；2.中国科学技术大学 工程科学学院，安徽 合肥 230026）

1 研究背景

济南市素有“泉城”的美誉，辖区内分布多处名泉，其中尤以趵突泉最为著名。而今由于社会经济和城市化进程的不断推进，使得泉水补给区面积骤减，大量新增的硬化面积，削弱了泉域岩溶水的补给量，破坏了区域地下水系统的自然平衡状态，近年来，泉水分布区地下水位的持续下降，使得泉水喷涌受到严重威胁［1-2］。为了保障泉水的持续喷涌，缓解日益突出的水资源供需矛盾，济南市在启动引黄供水工程的同时充分利用南水北调东线的水源，将外调水与当地地表水相结合，在泉域岩溶水的直接补给区开展回灌补源工程。

随着济南市保泉供水工作陆续开展，王庆兵等［3］设计了4类地下水资源开采方案，运用地下水流数值模型模拟了4种方案对泉群地下水水位及泉水流量动态变化的影响，最终确定泉域地下水可持续开采方案。高宗军等［4］采用微量元素水文地球化学方法，对济南泉域范围内的丰枯水期岩溶水化学特征及其变化进行调查研究。邢立亭等［5］采用示踪试验、泉水位动态观测等方法揭示济南岩溶含水介质特征。张展羽等［6］针对地下水位在时间序列上表现出高度的随机性和滞后性，建立了基于主成分分析与多变量时间序列CAR模型，对泉域内岩溶水水位进行预测。齐欢等［7］利用地下水数值模拟GMS软件对玉符河补源进行评价，提出西郊水位的抬升可以缓解地下水开采对趵突泉水位的影响，减小保泉的压力。

本文借鉴已有的研究成果，从保泉供水、区域地下水资源保护的角度出发［8］，结合济南泉域岩溶水补给区的水文地质特征和现有的回灌补源工程，利用灰色动态GM（1，1）和时间序列ARIMA、Holt-Winters三种模型分别对趵突泉历年的水位数据进行评价分析，并选择拟合效果最优的模型对泉水位的波动趋势进行预测，为济南市水生态文明建设及泉水资源保护提供依据。

2 研究区概况

济南市位于山东省中部，面积8154km2，属暖温带季风气候，多年平均降雨量为647.9mm，在6—9月集中降雨，占全年降雨量的70%，大气降水是济南岩溶地下水最主要的补给来源，降雨量的多少直接决定区域内岩溶水资源的总量［9］。岩溶泉域位于济南中部，为一复杂的岩溶水系统，对济南泉域的划分尚存在争议，目前普遍认同的观点为：南边界为玉符河、北大沙河源头的地表水分水岭（即长城岭），北边界为济南北部的石炭、二叠系地层和岩浆岩体，东西两侧分别以济南东部的东坞断层和长清附近的马山断层作为弱透水边界与外界发生水力联系，泉域总面积1500km2［10］。趵突泉的泉水主要来源于南部山区，大气降水及地表径流通过灰岩出露和裂隙岩溶发育的地带入渗形成裂隙岩溶水，该部分水流沿岩层倾斜方向由南向北运动，至城区受到火成岩岩体的阻挡而大量汇聚，在灰岩和侵入岩体的接触地带及第四系沉积层较薄弱处形成泉水涌出地表［11］。济南泉域范围及趵突泉位置见图1。

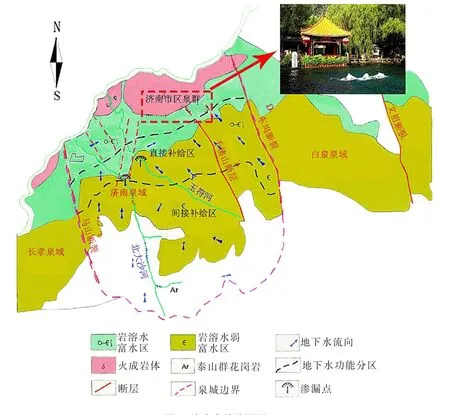
图1 济南泉域范围图

3 研究方法

3.1 灰色时间序列模型简介对灰色系统建立的预测模型称为灰色模型（Grey Model），简称GM模型，通过少量的、不完备的信息，建立灰色微分预测模型，对事物发展规律作出模糊性的长期描述［12］。时间序列分析是根据系统观测值得到的时间序列数据，通过拟合逼近和参数估计来建立数学模型对观测序列进行评价预测［13］。地下水位波动成因复杂，是典型的灰色系统，本文选取了济南泉域趵突泉近5年的地下水位进行分析，并采用三种灰色时间序列模型对趵突泉的水位进行拟合，通过比较三种模型的拟合结果，选择最优模型对济南泉域的地下水位进行预测、评价。3种模型适用条件及优缺点对比见表1。

表1 3种灰色时间序列模型适用条件及优缺点对比［14］

3.2 模型分类（1）GM（1，1）模型。已知观测序列经过一次累加生成序列（1-AGO），建立灰色微分方程：

记则由最小二乘法使得J(u)=(Y-Bu)T(Y-Bu)取最小值，u的估计值为：

预测方程为：

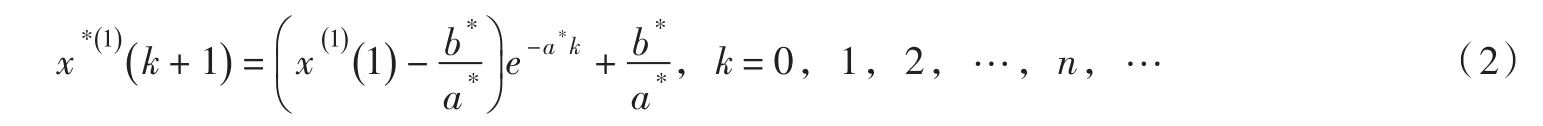
式中：x(0)(k)为观测值序列，x(1)(k)为一次累加序列，u为参数向量，Y和B为参数矩阵，a为发展系数，b为灰色向量，t和k为时间响应值，u*为u的估计值，x*(1)(k+1)为预测值。

（2）ARIMA模型。模型表达式为：

其中等式左边的模型是自回归AR（p）部分，非负数p表示自回归阶数，{φ1，φ2，…，φp}称为自回归系数；等式右边是移动平均MA（q）模型，非负数q称为移动平均阶数，{θ1，θ2，…，θp}称为移动平均系数，εt为随机干扰误差项，将观测序列进行d次差分，作平稳化处理。

（3）Holt-Winters模型

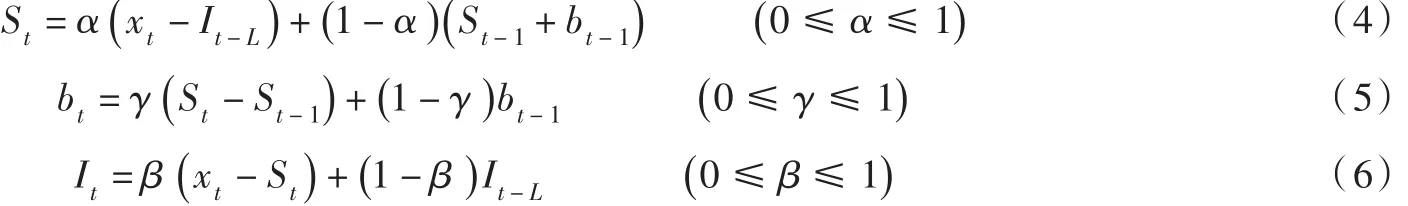
预测方程为：

式中：St为平滑值即水平分量，α为水平权重；b为长期趋势值，γ为趋势权重；It为季节分量，β为季节权重；L为季节长度（每年的月数或季数）；t为当前时间；xt为是实际观测值；yt+k为预测值，k为预测超前期数。

4 趵突泉地下水位预测

4.1 趵突泉水位波动分析对2012年5月至2017年12月济南泉域趵突泉的地下水位数据进行分析，水位变化的时序图见图2，2010—2017年济南市降雨量与地下水开采量见表2。

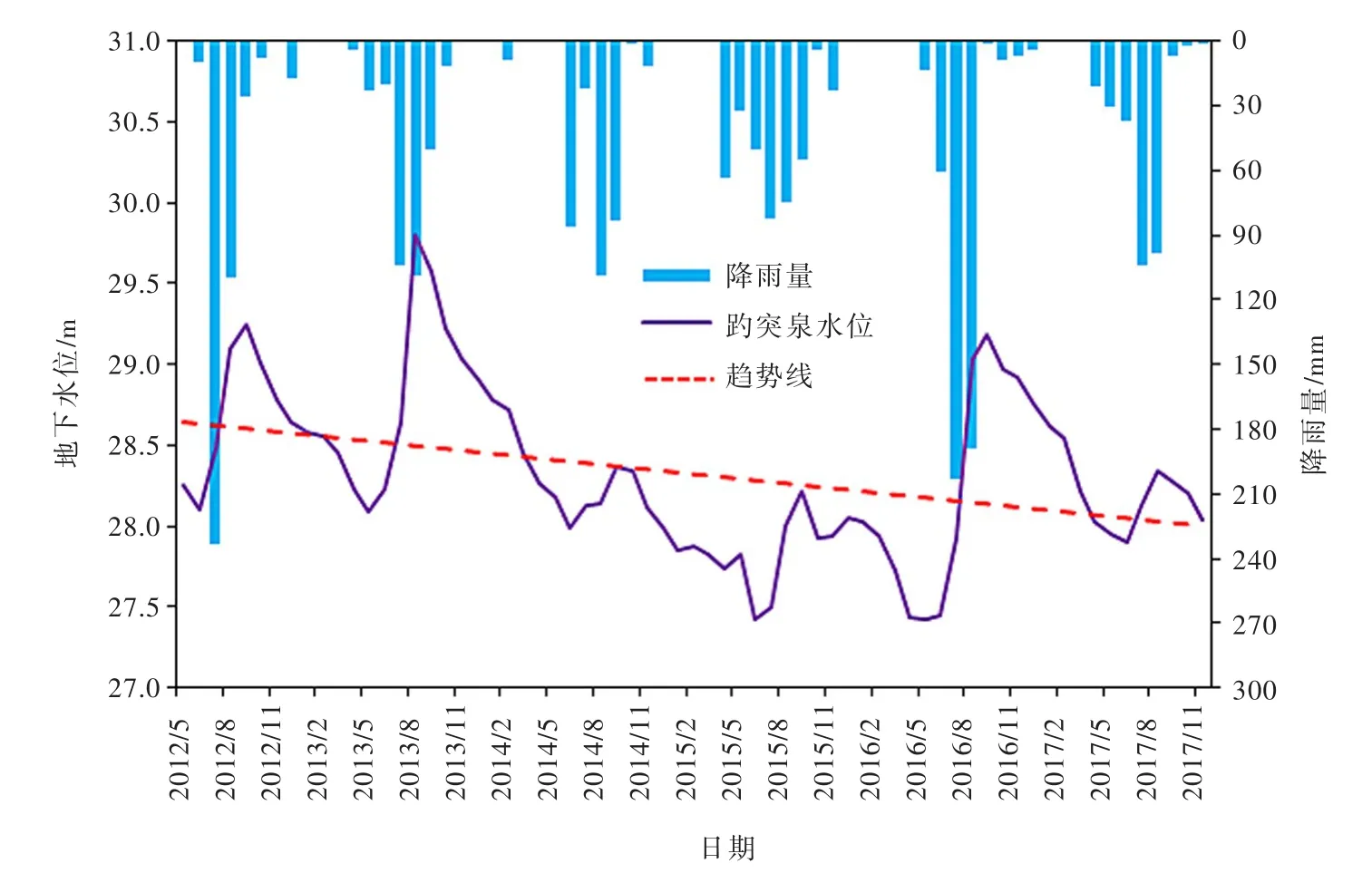
图2 趵突泉地下水位变化时序图

由图2可以看出趵突泉的水位整体呈现下降趋势，在每一年中水位随着季节的变化出现波动并且表现出一定的规律。每年3月地下水位开始下降，5—6月份下降幅度最为迅猛，主要原因是：3月份入春之后，天气干燥，气温回升块，降水少且蒸发量大，土壤失水量大。5—6月份随着济南市西郊春耕的陆续开始，大量抽取地下水用于农业灌溉，导致地下水位迅速下降，7月份之后由于春耕逐渐结束，大规模用水接近尾声，趵突泉水位止跌回涨，7—9月份雨水较为丰富，降雨形成的地表径流入渗补给深层岩溶水使得泉域地下水位逐渐抬升，9月地下水位波动达到峰值。济南位于鲁中地区，冬小麦最佳的播种期为10—11月，因此，10月份之后由于降水减少加之冬灌对地下水的开采使得水位出现回落［15］。全年来看，影响地下水位的主要因素是季节性开采和降雨，每年4—7月的春耕季节性开采，使得全年中这一时期的水位最低，该时期的泉水位是保泉供水的重点监控水位［16］。在降雨量较小且泉域地下水开采量较大的情况下，若不及时开展回灌补源工程，济南市的四大泉群将面临停喷危机。

双顶径是指胎头两个顶骨隆突间的距离。位置约为两侧太阳穴上方最宽处骨头之间的长度。随着孕周的增加，胎儿双顶径逐渐增大，孕足月时平均值约为9.3厘米。在分娩的过程中胎儿的头部通过产道的最大径线就是双顶径。

分析表2可知，济南市近4年中：仅2016年为平水年，连续3年遭遇枯水年，降雨量整体偏少使得岩溶水的补给量骤减。另一方面，目前济南市的地下水开采布局，主要还是集中开采泉域内的东部地下水，济西岩溶水开采量较小，据济南市名泉办统计，目前济东地下水集中开采区，日开采量22万吨。同期地下水开采量虽有降低但降幅较小，因此，在现状开采条件下，趵突泉水位呈现出下降趋势。

4.2 数据的预处理及模型训练灰色时间序列数据与普通数据不同，它要求建模数据必须为光滑离散数据并且具有严格的顺序，需要定义灰色时间变量以满足模型要求，分别对观测数据进行1次累加和1次差分，使数据平滑化。GM（n，1）模型通过多次拟合及后验差检验，最终选择1阶线性动态GM（1，1）作为预测模型；对ARIMA模型进行反复训练，其中自回归阶数p为1，移动平均阶数q为1，并进行1次季节差分时，模型ARIMA（1，0，1）（1，1，1）对观测值的拟合效果较好。Holt-Winters模型经测试最终选择Holt-Winters加法模型进行优化拟合时模拟精度较高。

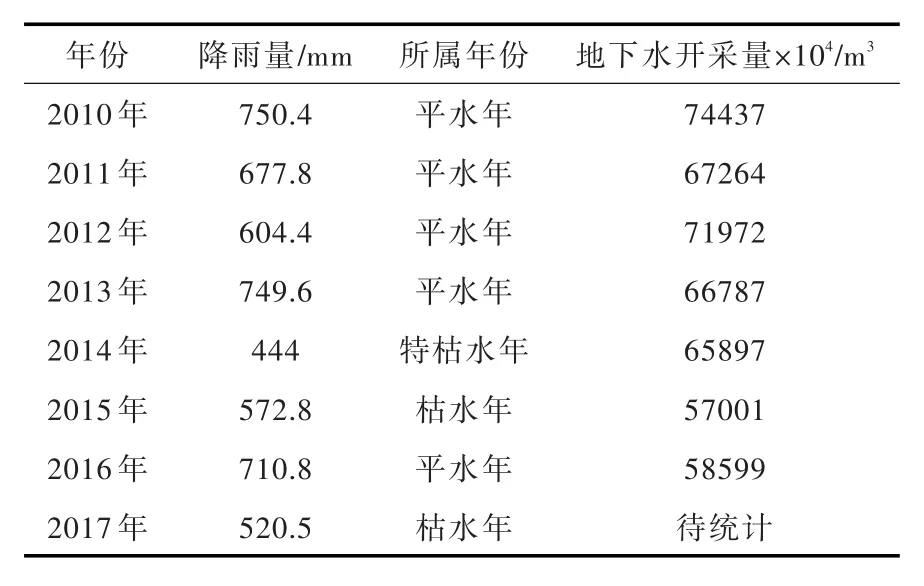
表2 2010—2017年济南市泉域降雨量与地下水开采量

4.3 数学模型的比选借助MATLAB数据处理软件，采用3种灰色时间序列模型，对趵突泉2012—2017年逐月地下水位数据进行分析，并选取3项指标对模型的拟合结果进行检验：利用确定系数（R2）检验拟合值与观测值的相关程度；均方根误差（RMSE）检验拟合数据的可靠性；效率系数（NSE）对水文模型的预测能力进行评价。观测值与拟合值时序图见图3—图5，模型的检验见表3。

由图3—图5可见，ARIMA与Holt-Winters模型与实际观测序列的变化趋势高度相近且模型较为成功的预测了水位波动的峰值和谷值，可以判定使用该模型是较为合理的；而灰色动态GM（1，1）模型仅成功的捕捉到了水位下降的趋势，对地下水位的周期性、季节性波动变化趋势的拟合并不理想。

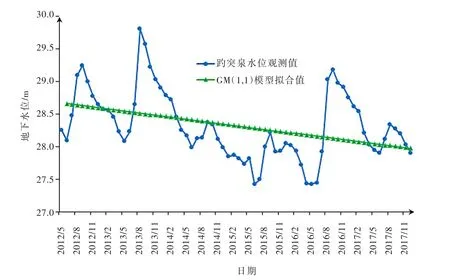
图3 GM（1，1）模型拟合值与观测值时序图

图4 ARIMA模型拟合值与观测值时序图

图5 Holt-Winters模型拟合值与观测值时序图

表3 模型拟合情况检验表

表3给出了三种模型的拟合、预测情况检验表，可以看出GM（1，1）模型的拟合、预测情况均最差，决定系数R2和效率系数NSE数值均为最低，并且误差项RMSE数值较大，说明利用该模型分析趵突泉水位波动规律精度较差，因此，不考虑使用GM（1，1）模型。时间序列ARIMA与Holt-Winters模型的拟合效果整体较好，3项检验指标数值较为接近，差异不明显，需要对拟合情况进行深入分析。综合以上的分析结果，对趵突泉的地下水位分析、预测优先使用ARIMA与Holt-Winters模型。

表4 ARIMA与Holt-Winters模型的拟合优度指标

为了探寻对趵突泉水位波动规律拟合效果最佳的模型，分别对ARIMA与Holt-Winters模型选取了8项拟合优度指标进行对比分析，由表4可知：两个模型均无离群值（逸出值）且平稳的R2数值较大，说明建模数据为平滑的离散序列，数值较为可靠；Ljung-Box Q检验结果显示系统残差为高斯白噪声，表明模型的设定较为合理；为防止模型复杂度较高引起过拟合现象，根据“BIC贝叶斯信息量准则”选择最优模型（BIC的值越小越好），结果表明：Holt-Winters模型对水位观测值的拟合效果优于ARIMA模型；此外，Holt-Winters模型的MAPE（平均相对误差绝对值）、MaxAPE（最大平均相对误差绝对值）、MAE（平均绝对误差）、MaxAE（最大平均绝对误差）评价指标均为最小，说明Holt-Winters相对于ARIMA模型的误差项更小，对原始数据的拟合精度更高。因此，综合考虑模型的合理性、复杂度及误差项等优度指标，最终选择Holt-Winters模型作为预测模型。

4.4 最优模型的应用通过对3种数学模型的深入比选，最终选择拟合效果最优的Holt-Winters模型对趵突泉的地下水位进行分析，并利用该模型预测了2018—2019年趵突泉的水位波动情况。Holt-Winters时间序列模型参数见表5，2018—2019年趵突泉水位预测值时序图见图6。

表5 Holt-Winters模型的参数估计表

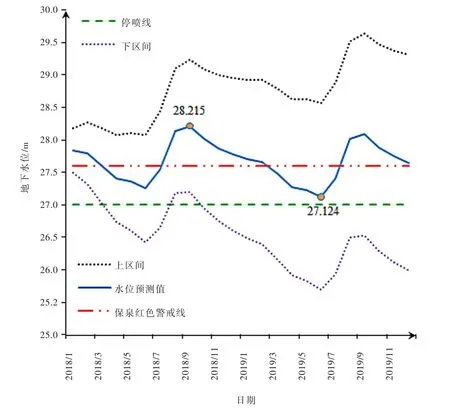
图6 观测值与拟合值、预测值时序图

随着济南市保泉工作的陆续开展，地下水开采量近年来已趋于稳定，由表2可知济南市近8年来降雨量持续偏枯，近10年中未出现丰水年，近20年中仅有2年为丰水年［17］。以近年的降雨与开采现状为依据，利用Holt-Winters模型预测短时期内的泉水位的波动情况，并以此为基础评价保泉形势。

图6给出了Holt-Winters模型的预测值、预测值95%的置信区间值，并标注出了水位波动的峰值、谷值及保泉红色警戒线、泉水停喷线。

4.5 预测结果分析利用Holt-Winters模型对2018年1月至2019年12月趵突泉的地下水位进行预测，由图6可知：趵突泉的地下水位在未来的24个月总体呈现出下降趋势且水位标高均值分别为27.734m和27.605m，2019年6月泉水位预测值为近7年最低水平，数值仅为27.124m，低于《济南市保持泉水喷涌应急预案》规定的27.6m的保泉红色警戒线，逼近27.01m的停喷线。表明现状降雨与开采条件下趵突泉在2019年6月可能存在潜在停喷危机。由此可见，济南市未来两年内“保泉”形势依然严峻。

表6 2013—2019年趵突泉年平均水位及峰值谷值对比 （单位：m）

由表6可知：2014、2015年济南市连续遭遇枯水年，农业灌溉对地下水的季节性开采量相对较大而有效补给量偏少，趵突泉水位下降明显；近4年中仅2016年为平水年，降雨量总体偏枯。济南市政府及时启动保泉应急预案，加大了外调水源的使用力度，关停了泉域范围内的部分自备井，在一定程度上缓解了水位下降势头，使得泉水位出现小幅上涨，但由于降雨量并未明显增加，深层岩溶水的有效补给量增长并不显著，地下水超采形成的局部降落漏斗在短时期内未能得到完全修复，使得泉水位难以持续上涨。Holt-Winters模型的预测结果表明：2018和2019年的泉水位预测值与2013—2017年同期的多年平均地下水位观测值相比分别下降了53.4cm和66.3cm，降幅为1.9%和2.4%，水位下降幅度较大，且仍然存在不断下降的趋势，采用必要的调蓄补源措施已迫在眉睫。

5 结论

通过对趵突泉2012—2017年逐月的地下水位变化规律进行分析，得出泉水位既存在不断下降的趋势，又受季节变化的影响呈现出明显的周期性波动，因而，采用灰色时间序列模型对趵突泉的地下水位进行分析预测较为合适。对3种模型水位观测值拟合效果进行检验，初步确定ARIMA与Holt-Winters时间序列模型的预测效果要优于灰色动态GM（1，1）模型，再分别选取8种拟合优度指标对ARIMA与Holt-Winters模型进行深入分析，最终选择拟合效果最优的Holt-Winters模型对趵突泉的水位进行预测，该方法的拟合优度、可信度及模型的预测能力均较好，适用于中、短期正常气象条件的地下水位预测。

采用Holt-Winters模型预测了2018—2019年2年内趵突泉的地下水位变化情况，预测结果表明2018、2019年的泉水位均值分别值为27.734m和27.605m，泉水位波动的峰值为28.215m、谷值为27.124m且谷值将出现于2019年的6月份，是近7年来的最低水位，该水位低于27.6m的保泉红色警戒线，逼近27.01m的泉水停喷线，照此趋势发展，若无法有效缓解水位下降的势头，在2019年6月趵突泉泉水可能面临潜在的停喷危机。