水库汛限水位实时动态控制方案优选研究

张艳平，张双虎，周惠成，王海军

（1.中国水利水电科学研究院，北京 100038； 2.大连理工大学，辽宁 大连 116024；3.水利部 水土保持监测中心，北京 100055）

1 研究背景

水资源短缺严重制约了我国经济社会发展。国内外学者提出“洪水资源化”概念，并开展了大量关于水库汛限水位动态控制研究，旨在不降低水库自身及上下游防洪安全的前提下，通过动态控制水库的汛限水位来增加洪水资源利用率。经过多年研究及实践证实：水库汛限水位动态控制是实现洪水资源化、提高洪水资源利用率的有效措施之一［1-8］。实际上，水库汛限水位动态控制是十分复杂的，虽然汛限水位动态控制域的研究为汛限水位实时动态控制制定了一个约束范围［4-5］，但这个约束范围却不能替代实时调度阶段的汛限水位动态控制决策值。一次洪水过程中，汛限水位动态控制决策值的大小不仅影响水库的防洪风险，而且关系到水库在汛期及汛后蓄水量的多少。若汛限水位动态控制决策值偏低，虽较高程度的保证了防洪安全，但有可能导致洪水过后无水可蓄；若汛限水位动态控制决策值偏高，虽可增加一定的兴利效益，但相应防洪风险可能增加。因此，从防洪安全和兴利效益角度出发，有必要研究合理的水库汛限水位动态控制决策方案。

不同的汛限水位动态控制方案对应不同的防洪风险和兴利效益，属多目标群决策问题［2］。需要优选的决策方案具有多目标性特点，可能同时存在定量与定性目标，很难得到最优解而在于寻求满意解。目前，关于求解满意解的方法大致可分为两大类［9］：一类是多目标多模型递阶分析法，如AHP法、多目标多模型层次递阶控制法等；另一类是多阶段多层次多目标模糊优选满意决策方法，如多目标多阶段模糊优选模型、系统层次模糊优选模型和可变模糊优选模型等。

实际上，汛限水位实时动态控制方案优选选择上述任一模型均可，但从简化的角度，协调折中方案优选过程中的效益和风险问题，本文在可行的汛限水位动态控制方案集［8］已明确的基础上，选取水库汛限水位实时动态控制方案优选评估指标，采用基于协商对策的多目标群决策模型［10］求解得到水库汛限水位实时动态控制满意决策方案。为消除单一权重法的片面性，在确定决策者赋予各指标的权重时，分别采用二元对比法［11］确定其经验权重、熵权法［12］确定其数学权重，最后应用基于博弈论的组合赋权法［13］综合考虑其经验权重和数学权重，从而得到一个更为均衡的组合权重。以大伙房水库为例，详细阐述该模型在水库汛限水位实时动态控制方案优选中的应用和决策过程。

2 水库汛限水位实时动态控制方案优选模型

2.1 基于协商对策的多目标群决策模型［10］在多目标群决策模型中，设定A、B为有冲突的决策者，C为仲裁者，构成由三方参与的仲裁局势。由A、B分别向C提供各自认为满意的若干可行方案，C根据A、B提出的方案，结合全局利益，依据公平原则，优选出最佳方案作为最终决策，且C具有最终决定权。一般情况下，冲突一方若想让对方接受自己的方案，需同时考虑双方均关注的问题。则有双方共同需要考虑的目标x1，x2，…，xm( )m≥2。这些目标，有的趋于一致，有的存在冲突。假定仲裁者C要求冲突双方均提供n个方案，则有A、B提供的目标值矩阵分别为：

其中，aij、bij分别为冲突者A、B提交给仲裁者C的第i个方案的第j个目标值，i=1，2，…，n，j=1，2，…，m。

A、B、C三方构成仲裁局势，记为M=(A，B；x1，…，xm；C)，采用两阶段规划进行求解。

（1）效用均衡规划：

（2）边际效用规划：

式中：SFA(X)、SFB(X)分别为A、B方关于x1，x2，…，xm的综合满意函数；X0为第一阶段的仲裁解；X=(x1，x2，…，xm)T为解向量；S为约束条件集。

仲裁者C根据式（1）提供的信息构造满意函数。

关于效益型指标，A、B的满意函数分别为：

关于成本型指标，A、B的满意函数分别为：

设冲突者A、B在提交方案时，相应的确定各目标的权重分别为α=(α1，α2，…，αm)T，β=(β1，β2，…，βm)T，则A、B关于x1，x2，…，xm的综合满意函数分别为：

将式（6）中A、B的综合满意函数代入式（2）、式（3）即可得出最终仲裁解X*为仲裁者C根据A、B提供的信息得出的一种双方都可以接受的理想协调解。

为求得实际最佳协调方案，以X*为理想方案的目标状态，采用模糊识别方法选择一个最为接近X*的方案。需对式（1）进行归一化。记

关于效益型目标，归一化为：

关于风险型目标，归一化为：

A、B各方案对仲裁解X*的贴近度分别为：

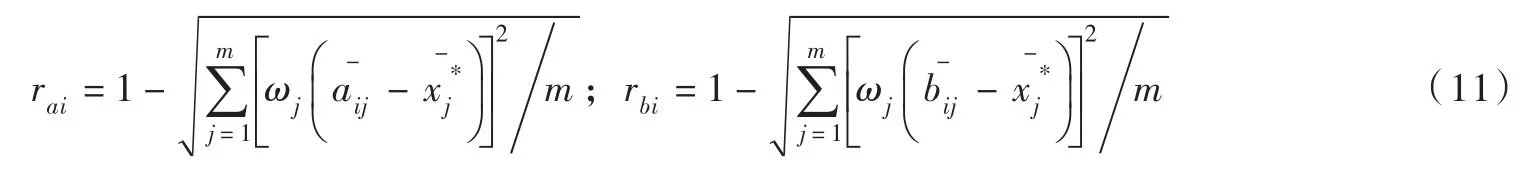
式中，w1，w2，…，wm为仲裁者C的目标权重，由max{ra1，ra2，…，ran，rb1，rb2，…，rbn} 求 出 仲裁结果。

2.2 指标权重的确定本文采用基于协商对策的多目标群决策模型进行汛限水位实时动态控制方案优选，作为方案的提供者A、B主要考虑个人经验，其权重为经验权重。仲裁者C作为方案的最终决策者，其给予各指标的权重应为组合权重，即综合考虑数学权重和经验权重。其中，经验权重采用二元对比法［11］，数学权重采用熵权法［12］，组合权重采用文献［9］和文献［13］中的基于博弈论的组合权重法来确定。基于博弈论的组合权重赋值法，可体现各方法之间相互竞争而又协调一致的思想，更科学、客观全面地解决权重的确定问题。

3 水库汛限水位实时动态控制方案优选指标和步骤

3.1 优选指标的确定在水库实时调度过程中，不同的汛限水位动态控制方案对应的泄流量、弃水量、发电量与供水、风险率及阶段调洪末水位等各项指标亦不同。这些指标中有些明显属于效益型指标，如发电量与供水；有些明显属于风险型指标，如调洪最高水位、最大下泄流量等。

因此，汛限水位实时动态控制方案所涉及的指标较多，且各指标间存在彼此竞争，甚至是矛盾关系。不同水库、不同的防洪兴利任务、不同阶段汛限水位动态控制方案优选的指标虽有所不同，但大致可概括为两类，即风险型和效益型［2］。

为了能够全面反映各汛限水位实时动态控制方案的优劣特性，本文以系统性和简明性等原则，参考文献［2—3］中汛限水位动态控制方案的目标体系。风险型指标选取校核洪水调洪最高水位和校核洪水最大下泄流量。校核洪水调洪最高水位是指调节校核标准的洪水过程所得的最高水位，该值越大则对大坝越不利，说明此方案越不安全；校核洪水最大下泄流量是指调节校核洪水过程时水库的最大下泄流量，其值越大，则下游越不安全；效益型指标选取水资源利用率和供水保证率可靠度［2］。水资源利用率为体现供水效益的指标之一，是指在实时调度阶段，不同汛限水位动态控制值相对于原设计汛限水位所提高的洪水资源利用率。供水保证率可靠度为供水效益的另一指标，文献［2］中给出供水保证率可靠度的定义和计算公式，且给出实时调度阶段汛限水位动态控制方案优选时供水保证率可靠度的计算方法。

3.2 优选步骤水库汛限水位实时动态控制方案优选属多目标群决策问题，涉及多目标、多阶段、多人决策，其主要步骤如下：（1）收集相应阶段的实时、预报信息与约束条件。实时信息包括：已降雨量、实测水位与入库流量、水库下泄流量等；预报信息包括洪水预报过程或退水预报过程，不同预见期的分级降雨预报；约束包括防洪安全指标、兴利安全指标和汛限水位动态控制域等。（2）根据相关部门的期望，明确方案优选的多个指标，形成目标体系，冲突部门A、B根据自己的偏好，提出各自的方案集，如式（1），并提供相应的指标权重向量，构造其综合满意函数式（6）。（3）根据两阶段规划进行求解，具体见式（2）—式（3），最终得出仲裁解，由式（7）—式（10）对A、B方案集合仲裁解进行归一化处理。（4）根据仲裁者C提出的目标权重，由式（11）求得冲突双方各方案相对于仲裁解的贴近度，根据贴近度给出各方案的排序，供决策者选定满意方案，以贴近度最大为最优。如决策者根据实时信息或知识与经验指令新的方案或目标权重，则需反馈到步骤（2）—（3）。

4 研究实例

大伙房水库位于辽河支流浑河中上游的辽宁省抚顺市境内，控制流域面积5437km2，是一座以防洪、灌溉和城市供水为主，兼顾发电和养殖等综合利用的多年调节大型水利枢纽工程，且具备汛限水位实时动态控制的前提条件。水库设计的防洪限制水位为126.4m，文献［8］采用分类预报调度方式分析当大伙房水库的汛限水位为128.0m时，仍可保证水库下游防洪安全和水库校核洪水大坝安全。则可认为大伙房水库的汛限水位动态控制域定为［126.4m，128.0m］。虽然在此范围内控制水库的水位，认为水库可以承担增加的风险，但由于风险和效益的并存，决策者必然存在决策冲突。

4.1 仲裁局势的确定本文假设大伙房水库面临时刻为一次洪水的退水段，且预报未来24h无雨或小雨（＜10mm），水库汛限水位动态控制域为［126.4m，128.0m］。在该控制域范围内，以0.2m为一个阶段，可生成8个可行的汛限水位动态控制方案。

汛限水位实时动态控制的主要矛盾是效益和风险的冲突。主要表现在：偏重防洪安全的决策者希望汛限水位尽量接近设计值；偏重兴利效益的决策者则希望汛限水位控制尽量接近其动态控制域的最上限。因此这两个决策者之间产生冲突，两方决策者即为冲突的A与B，A与B分别提出4个方案，均没有给出一个确定值；仲裁者C则由专家组组成，负责协调这两个决策者并仲裁满意的调度方案。由A、B方提供的决策方案如表1所示。

针对A、B提出的方案，分别计算各水位值对应的洪水资源利用率和供水保证率可靠度［2］，以及该水位下调节的校核洪水最高水位和最大下泄流量，这两个指标计算数据与文献［8］一致，均满足原设计防洪要求。计算的各指标值如表1所示。

4.2 模型求解由上述表1方案集，可得到目标特征值矩阵A1、B1。

决策双方提供方案时均按照各自的偏好，有各自偏重的一面，其中，A偏重防洪风险，B偏重兴利效益，因此其给定的目标权重采用二元对比法。分别为：A的权重：α=(0 .197,0.177,0.329,0.297)，B的权重：β=(0 .329,0.297,0.197,0.177)。

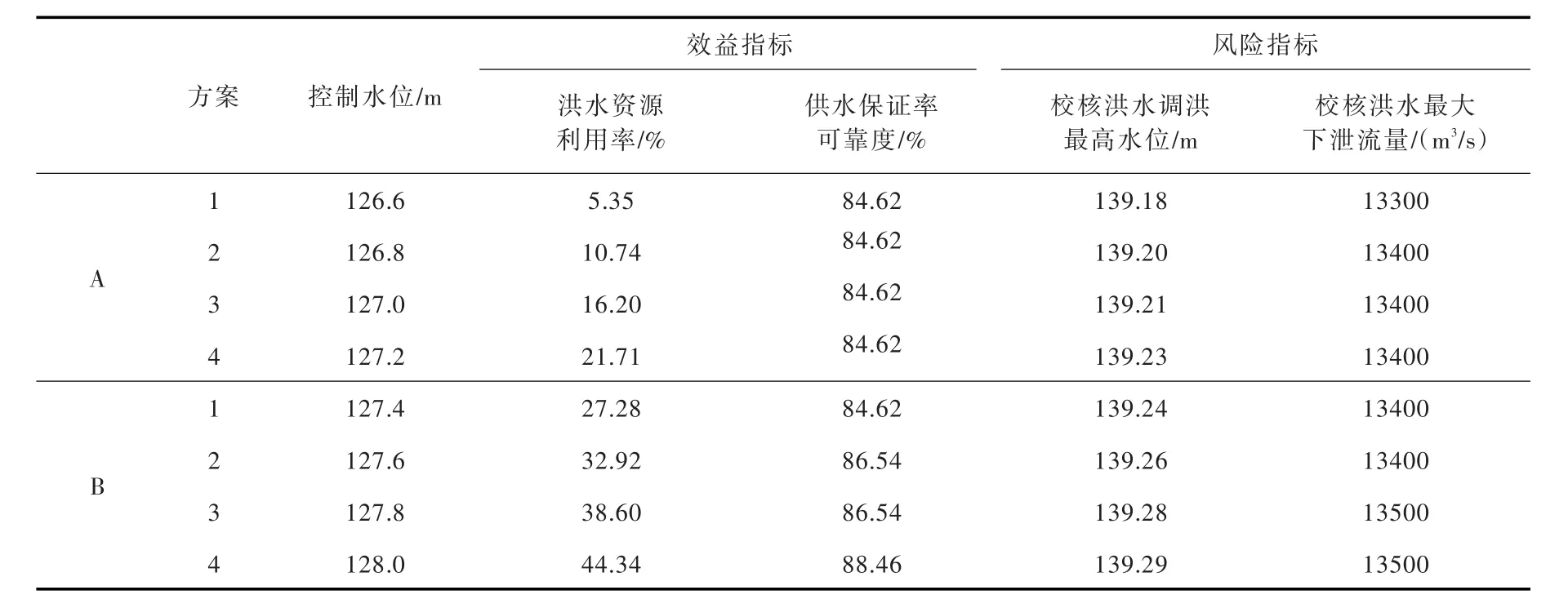
表1 A、B提供的方案集

根据式（4）和式（5）求得A、B的综合满意函数分别为：SFA(X)=0.0120x1-6.58x3-0.003x4+955.87，SFB(X)=0.0193x1+0.0773x2-3.94x3-0.0018x4+565.63。

解SFA(X)=SFB(X)得：0.0073x1+0.0773x2+2.64x3+0.0012x4=390.24。

形成第一阶段规划为：

得第一阶段最优解：X0=(3 8.03，84.62，139.18，13300 )。

解得目标函数值：SFA(X0)=0.6220，SFB(X0)=0.5960。

第二阶段规划SFA(X0)+SFB(X0)：

解得第二阶段最优解：X*=(4 4.34，88.46，139.18，13300 )。

得到A、B的满意函数值：SFA(X0)=0.6977，SFB(X0)=1.0145。

较第一阶段结果均有所改善，且B的改善明显。

为求得最后的决策方案，需利用式（7）—（10）对A、B的目标特征值矩阵和最优解X*进行归一化（见表2）。

仲裁者C作为方案的最终决策者，综合考虑冲突双方A、B的意见，协商后可能会提出3种目标的倾向方案：偏好防洪风险、偏好效益和同时看重。其给定的各目标权重采用组合权重法，即仲裁者C赋予各指标的权重分别采用文献［11］中的二元比较法计算其经验权重；采用文献［12］中的熵权法计算其数学权重；然后基于博弈论的组合权重赋值法求其综合权重。因此，仲裁者C决策的具体情况如下所述。

表2 A1、 B1与相应 X*归一化结果

（1）当仲裁者C偏重防洪风险。

二元对比法确定各指标权重：w1=(0 .197，0.177，0.329，0.297 )。

熵权法确定各指标权重：w2=(0 .254，0.253，0.262，0.231) 。

基于博弈论的组合权重赋值法确定各指标权重：w=(0 .200，0.181，0.325，0.294)

则A、B各 方 案 的 贴 近 度 由 式（11）计 算 得 ：Ta=(0 .8651，0.8520，0.8559，0.8503 ) ，Tb=(0 .8472，0.8508，0.7862，0.7809 )。

根据贴近度最大原则，由贴近度计算结果可知0.8651为最大值，仲裁者应选择A提供的第一个方案作为满意方案。即偏防洪安全时，汛限水位可控制在126.6 m。

（2）当仲裁者C偏好兴利效益。

二元对比法确定各指标权重：w1=(0 .329，0.297，0.197，0.177 )。

熵权法确定各指标权重：w2=(0 .254，0.253，0.262，0.231) 。

基于博弈论的组合权重赋值法确定各指标权重：w=(0 .333，0.299，0.194，0.174)

则A、B各方案的贴近度由式（11）计算得：Ta=(0 .7762，0.7875，0.8015，0.8115 )，Tb=(0.8201，0.8582，0.8532，0.8697 )。

根据贴近度最大原则，由贴近度计算结果可知0.8697为最大值，仲裁者应选择B提供的第4个方案作为满意方案。即偏重兴利效益时，汛限水位可控制在128.0 m。

（3）当仲裁者C效益与风险同时看重。

二元对比法确定各指标权重：w1=(0 .25，0.25，0.25，0.25 )。

熵权法确定各指标权重：w2=(0 .254，0.253，0.262，0.231) 。

基于博弈论的组合权重赋值法确定各指标权重：w=(0 .253，0.252，0.260，0.235)

则A、B各方案的贴近度由式（11）计算得：Ta=(0 .8215，0.8217，0.8299，0.8320 )，Tb=(0.8344，0.8669，0.8209，0.8248 )。

根据贴近度最大原则，由贴近度计算结果可知0.8669为最大值，即仲裁者应选择B提供的第二个方案作为满意方案。即同时看重防洪安全和兴利效益时，汛限水位可控制在127.6 m。

综上所述，大伙房水库汛限水位实时动态控制方案可定为：当仲裁者C偏重防洪风险时汛限水位控制在126.6 m；偏好兴利效益时则控制在128.0 m；当仲裁者综合考虑防洪风险和兴利效益时，最佳方案为水位控制在127.6 m。

4.3 计算结果分析基于协商对策群决策模型同时兼顾冲突双方和整体利益，该模型将决策者的满意度函数作为效用函数，分两阶段规划得出最优解。根据模型的求解结果，大伙房水库汛限水位实时动态控制的8个可行方案中，最佳方案为控制在127.6 m，该方案既充分考虑了水库的防洪风险又考虑其兴利效益。但鉴于水库汛限水位实时动态控制时的复杂性及不确定性，本文又用模型分别计算了当仲裁者C偏重防洪风险和偏重兴利效益时的结果，经模型计算后确定其决策值分别为126.6 m和128.0 m，这两个结果与实际调度工作中的主观经验决策值相符合。且在模型求解过程中，冲裁者C给予各指标的权重采用组合权重，综合考虑了数学权重和经验权重，消除了单一权重法的片面性。

5 结论

本文针对水库汛限水位实时动态控制多目标的矛盾性和群决策等特点，以寻求满意决策值为目标，将基于协商对策的多目标群决策模型应用于水库汛限水位实时动态控制方案优选，可得出以下结论：（1）该模型概念清晰，计算较简单，易于实现计算机编程，兼顾冲突双方和整体利益，具有可操作性和实用性。（2）以大伙房水库为例，根据仲裁者不同的偏好优选的方案为：当预报未来24h无雨或小雨（＜10 mm）时，洪水退水段，大伙房水库汛限水位实时动态控制方案集的8个可行方案中，最佳方案为127.6 m，该方案既充分考虑了水库的防洪风险又考虑其兴利效益；当仲裁者偏重防洪安全时，汛期大伙房水库水位控制在126.6 m；当偏重兴利效益时，水库水位可控制在128.0 m。因此，采用该模型优选出的方案可为决策者提供较为直观的决策依据。