无线紫外光散射通信中的改进CMA-FSE盲均衡算法

2019-03-28赵太飞刘龙飞王晶杨黎洋

通信学报 2019年3期

赵太飞，刘龙飞，王晶，杨黎洋

赵太飞1,2，刘龙飞1，王晶1，杨黎洋1

（1. 西安理工大学自动化与信息工程学院，陕西西安 710048；2. 西南科技大学特殊环境机器人技术四川省重点实验室，四川绵阳 621010）

无线紫外光散射通信系统具有严重的码间干扰和信号衰减问题，针对该问题，提出了一种基于信噪比估计的改进常模分数间隔均衡器（CMA-FSE）算法。该算法将分数间隔均衡器（FSE）和常模算法（CMA）结合起来对无线紫外光信道进行盲均衡，使用接收信号的均方值衡量输入信噪比来确定最佳迭代步长，保证均衡算法快速收敛。仿真结果表明，改进CMA-FSE算法能在各种信噪比下快速收敛，并有效抑制码间干扰，改善系统误码率性能。与现有算法相比，改进算法信道跟踪和噪声抑制能力更强。

紫外光散射通信；码间干扰；信道均衡；信噪比估计

1 引言

无线紫外光散射通信在一些复杂环境中有独特的优势，在军事战场和部分民用场景中有着重要的应用价值，所以近年来得到了较为广泛的研究。无线紫外光散射通信最主要的特点是非直视通信，这使得紫外光散射通信具有不需要精确对准、能越过障碍物、隐秘性高等优点[1]。非直视通信依靠大气中各种微型粒子对紫外光的强散射特性得以实现，然而，同样因为微型粒子对无线紫外光的强散射特性，脉冲信号会发生明显的展宽[2]，因而会产生严重的码间干扰[3]。并且紫外光信号在大气中的衰减十分严重，也容易受到各种天气的影响，所以无线紫外光散射通信到达接收端的信号功率较小，接收电路输出信号的信噪比普遍较低。为了提高无线紫外光散射通信系统的性能，采用合适的信道均衡技术减缓码间干扰的不良影响是十分必要的。

常用的信道均衡算法可以分为使用训练序列算法和盲均衡算法这2种。前者包括最小均方（LMS, least mean square）算法、递推最小二乘（RLS, recursive least square）算法、最大似然序列估计（MLSE, maximum likelihood sequence estimation）算法等；后者包括Bussgang类盲均衡算法、基于高阶或循环统计量算法等。LMS和RLS都是以均方误差作为代价函数的信道均衡算法[4]，LMS算法计算简单但收敛较慢，RLS算法收敛较快但因为矩阵计算较多，所以时延较大。MLSE算法的原理是已知接收序列，确定发送序列使接收序列的条件概率密度最大，是一种最优均衡器[5]。但MLSE算法的计算复杂，不满足通信信号的低时延要求。盲均衡器是指没有训练序列，只根据输入信号本身就可以产生与期望信号相近的输出。Bussgang类盲均衡器是在均衡器输出端加一非线性变换计算出预期信号[6]，但算法在小信噪比时不易收敛。另外，高阶统计量也可以用于信道均衡[7]，但因为计算复杂、高阶统计量估计误差大等问题，在实际使用中的性能没有明显的优势。

分数间隔均衡器（FSE, fractionally spaced equalizer）等效于匹配滤波器后接波特间隔均衡器[8]，所以在小信噪比下也有较好的均衡效果，但训练序列需要占用一定的带宽，会降低有效通信速率，这对于窄带宽的无线紫外光散射通信系统是不可忽视的。常模算法（CMA, constant modulus algorithm）是一种利用信号恒模特性的盲均衡算法[9]，将其与FSE结合可得到FSE均衡器的盲实现方法，即CMA-FSE均衡器，既能在低信噪比（SNR, signal-to-noise radio）时有较好的均衡效果，同时也不需要占用额外的带宽。CMA-FSE均衡器在不同SNR时的最佳迭代步长不同，所以本文在对接收信号SNR进行估计的基础上提出了最佳步长计算方法，改进后的CMA-FSE均衡器能有效改善无线紫外光散射通信系统的可靠性和误码率性能。目前，紫外光散射通信系统以强度调制/直接检测为主，为方便研究分析，本文研究均基于二进制起闭键控（OOK, on-off keying）信号调制格式。

2 非直视无线紫外光散射信道模型

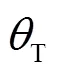
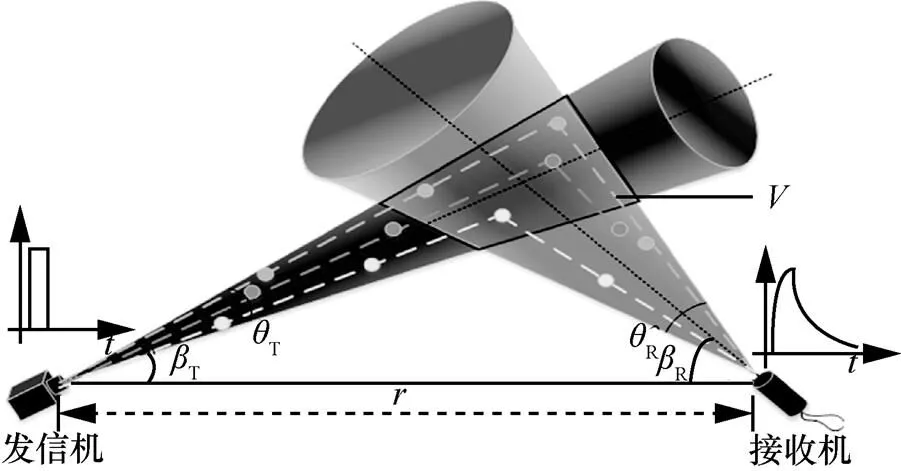
图1 非直视紫外光单次散射链路模型

将无线紫外光的单次散射链路分解为级联的2个直视链路[10]，建立椭球坐标系，可以得到如式(1)所示的接收辐照度的表达式。

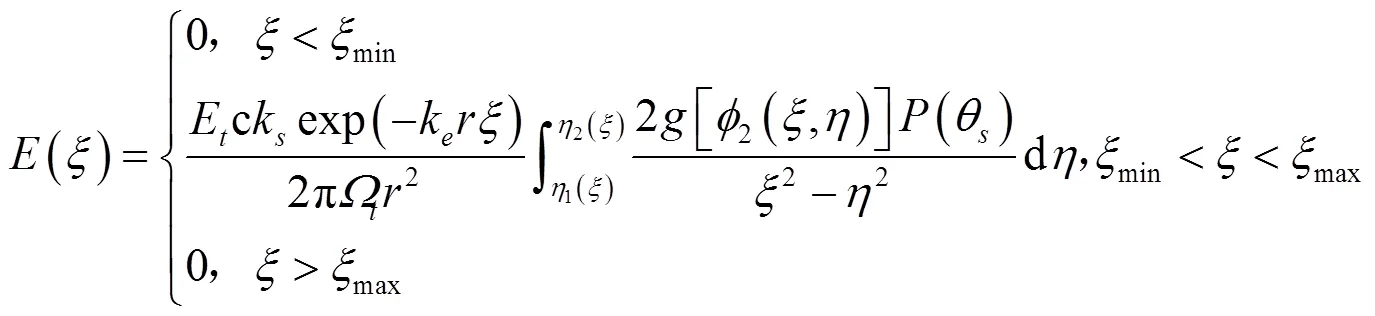
但该方法比较复杂，不方便计算和分析，文献[12]提出了采用伽马函数近似表示无线紫外光信道脉冲响应的方法，信道脉冲响应为

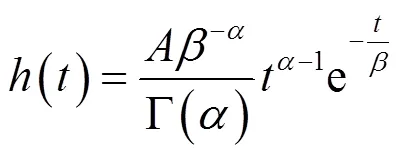
实际的无线紫外光散射通信系统中噪声分布情况比较复杂。系统接收端通常采用光电倍增管（PMT, photomultiplier tube）进行紫外光信号检测。PMT在无光环境下仍会有微弱的电流输出，经放大后会转换为噪声电压[13]。文献[14]中实验测量表明暗电流噪声和热噪声频谱近似为白噪声。另外，无线紫外光散射通信一般采用“日盲”波段[15]，地面附近背景噪声很小。以上分析表明无线紫外光散射通信系统的噪声分布以白噪声为主，所以本文用高斯白噪声作为接收信号中的噪声模型。接收信号的离散表达形式为

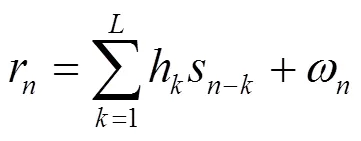
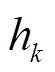
3 改进的CMA-FSE盲均衡算法

3.1 分数间隔均衡器

图2 间隔分数间隔均衡器原理框架

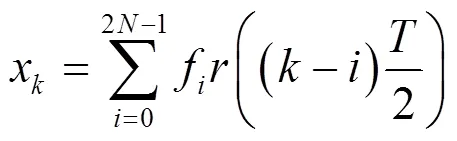
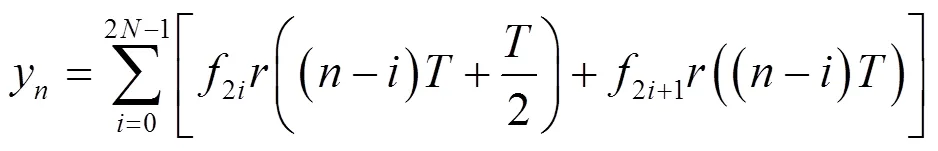
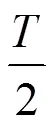
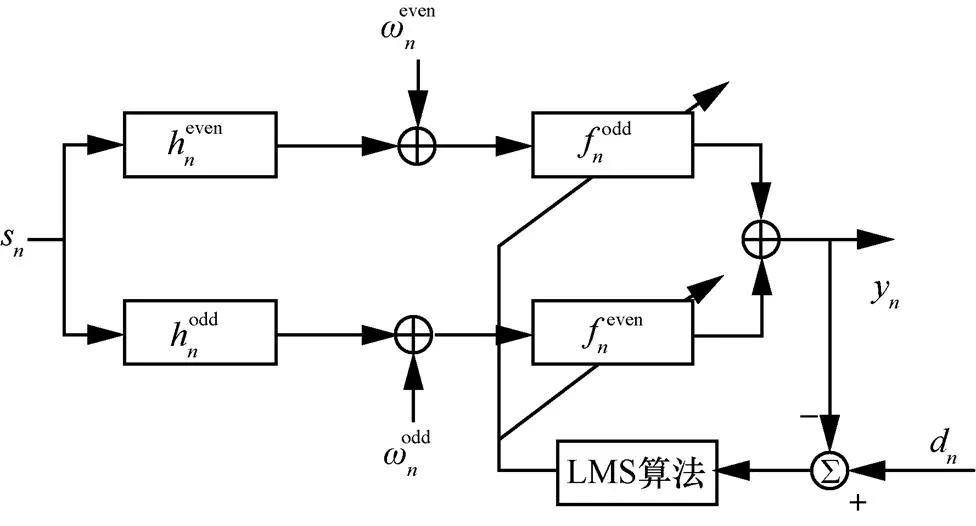
图3 间隔FSE的等效自适应多信道系统模型

3.2 改进CMA-FSE算法

数字调制通信具有恒模特性，即信号包络是基本固定的，CMA是一种基于恒模特性的LMS算法。代价函数定义为

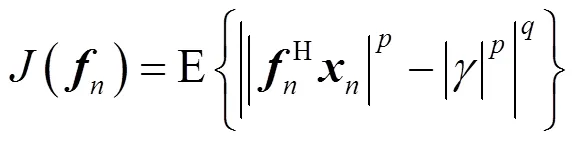
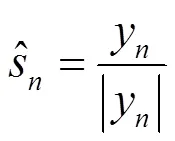
式(7)可以提取接收信号中的常模信号，但只适用于零均值的双极性编码。由于无线紫外光散射通信系统的特点，接收信号只能是单极性信号，因此在采用CMA均衡时，需要用接收信号减去均值，进行双极性化处理。在CMA-FSE均衡算法中，以FSE均衡器代替CMA中的LMS均衡器，FSE中的期望信号同样可由式(7)给出。

CMA-FSE算法的均衡效果主要通过收敛速度和输出信号的稳态均方误差来衡量。选取的迭代步长越大，收敛速度越快，但稳态均方误差较大；迭代步长越小，则情况相反，因此可以采用变步长算法，好处在于误差较大时采用较大的步长快速收敛，误差较小时采用小步长精确搜索极小值。另外，接收到的光信号功率会受到天气、环境、收发端相对运动等因素的影响而发生变化，所以有用信号的功率会发生变化，进而使得SNR发生变化。由于盲均衡算法在SNR较小时由式(7)给出的期望信号错误概率较大，大的迭代步长会使CMA-FSE算法变得极易发散。若采用小迭代步长，当SNR较高时，收敛速度无法达到最优值。而无线紫外光散射信号易受环境变化的影响，信噪比会经常发生变化，所以为了提高算法对各种信道情况的适应性，可以结合信号SNR与变步长算法，给出最佳迭代步长的计算方法。

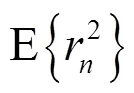
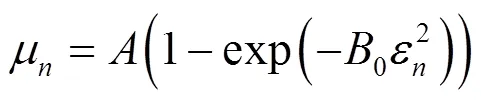
其中，有

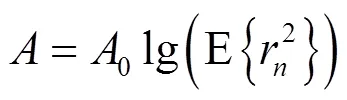
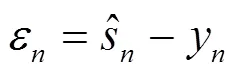
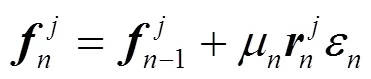
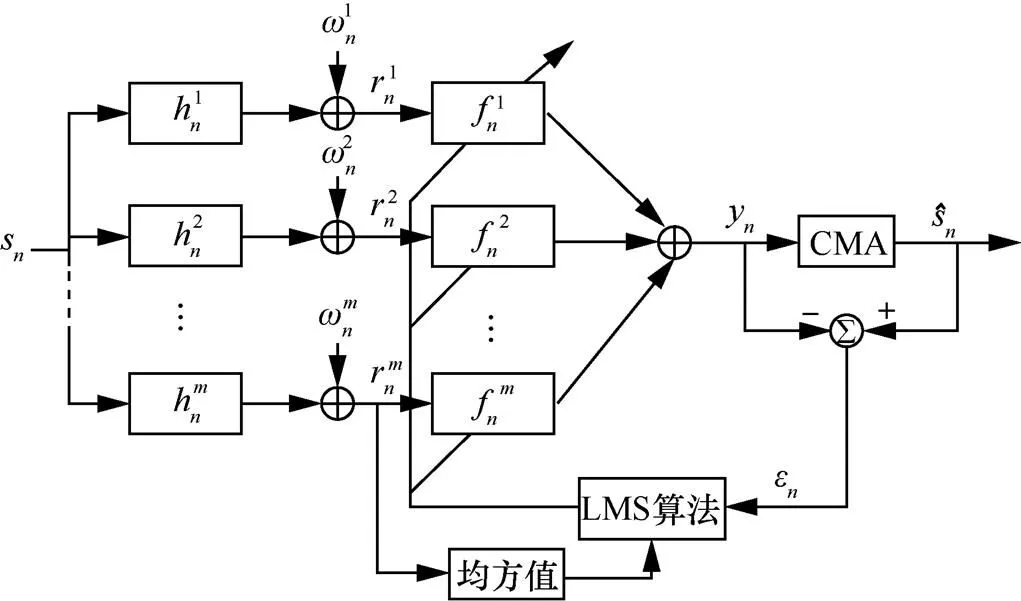
图4 间隔的等效多信道改进CMA-FSE算法框架

4 算法性能仿真分析

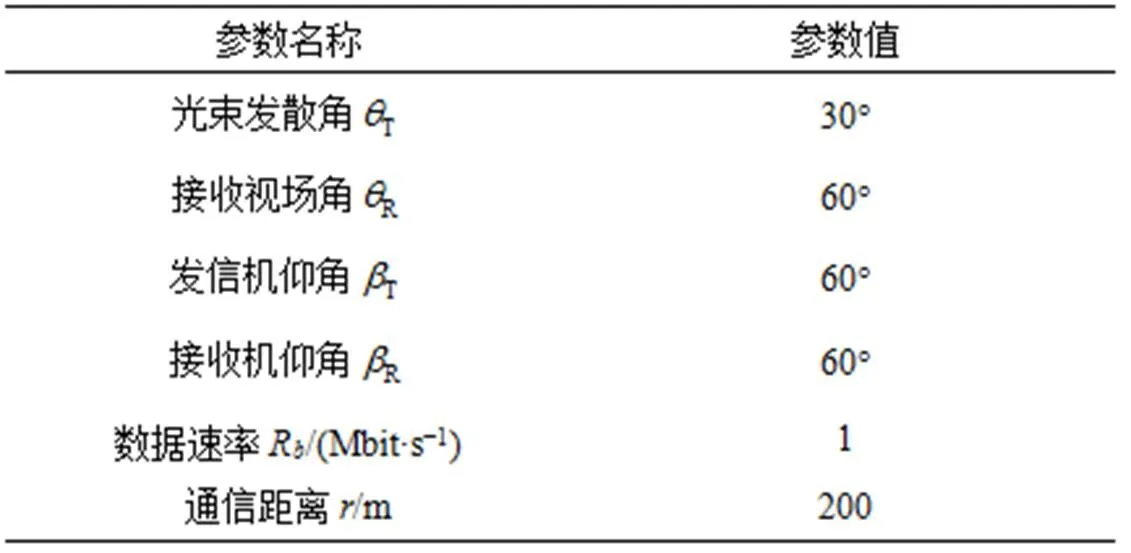
本节使用数值仿真的方法对改进CMA-FSE算法进行性能验证和分析。为了便于对比均衡算法的性能，本文调制方式均采用OOK调制。无线紫外光散射通信信道参数如表1所示。表1中的信道参数仅用于计算归一化信道脉冲响应，路径损耗在仿真中将以给定信噪比的形式体现。

表1 无线紫外光散射通信系统参数

4.1 各均衡算法的对比分析

从收敛速度和误码率这2个方面横向对比LMS算法、RLS算法、CMA-LMS算法和改进后的间隔CMA-FSE算法，并对各算法的综合性能进行分析，结果分别如图5和图6所示，图6还与未均衡时的误码率进行了对比。

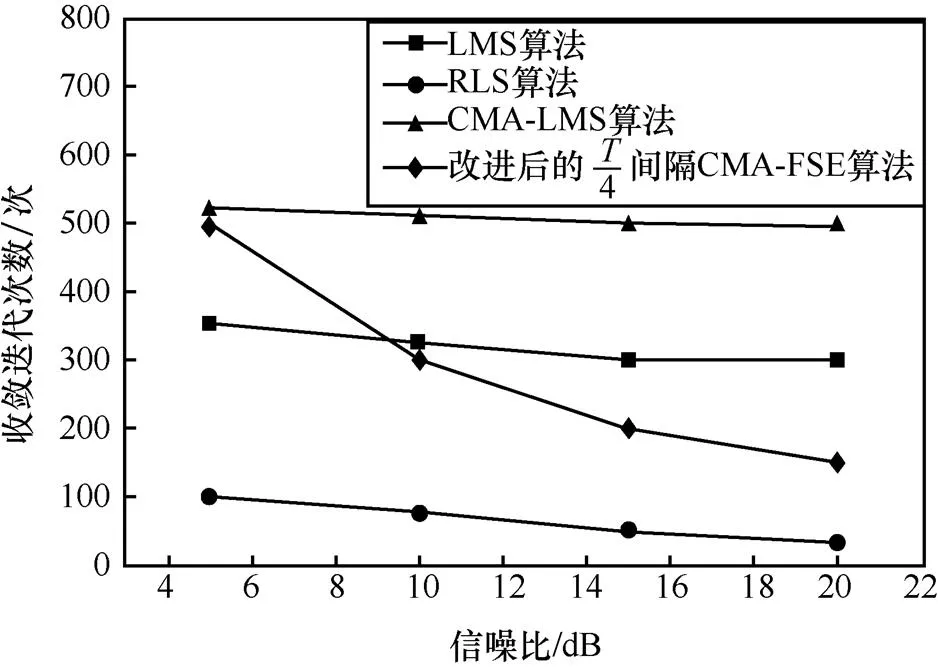
图5 各算法收敛速度对比

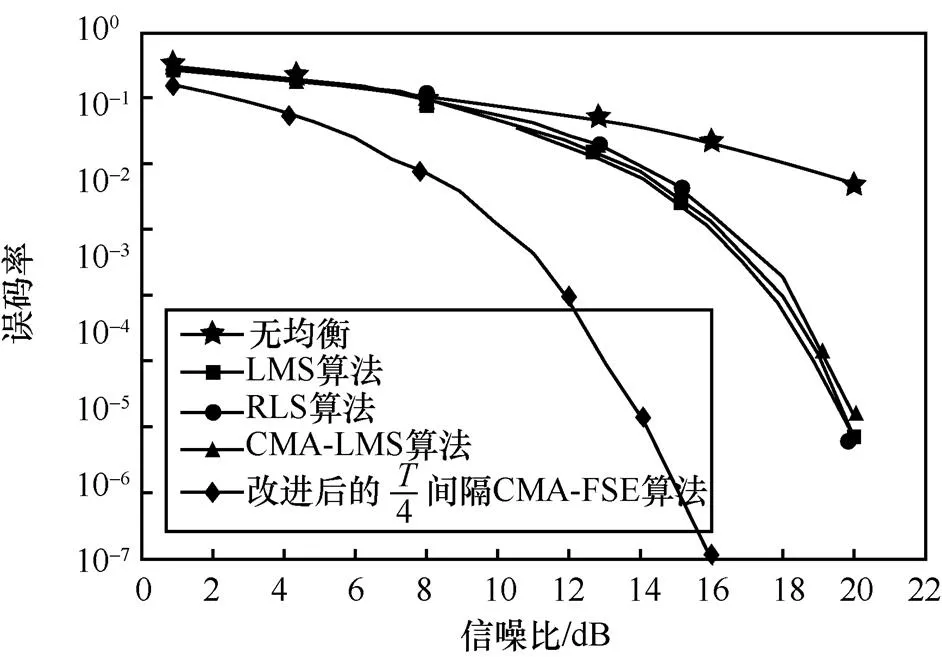
图6 各算法误码率对比

LMS、RLS和CMA-LMS这3种算法都是固定步长的，从图5可以看出，它们在给定步长时的收敛速度随信噪比变化不大，RLS算法收敛速度最快，LMS算法次之，CMA-LMS算法最慢。这是因为CMA-LMS算法是盲均衡算法，收敛初始阶段期望信号误差较大，需要多次迭代才能收敛。虽然RLS算法收敛很快，但RLS算法是基于训练序列的算法，且由于矩阵运算较多，算法时延较大。这3种算法在小信噪比时虽然也能收敛，但稳态均方误差都较大。而改进CMA-FSE算法随着信噪比增大，收敛迭代次数快速减小，能够有效跟踪信噪比变化，使算法在收敛速度和稳态均方误差之间达到良好的权衡。

从图6可以看出，LMS算法、RLS算法和CMA-LMS算法这3种算法都能降低误码率，但当信噪比小于10 dB时，几乎没有任何作用。这3种算法的误码率曲线近乎重合，说明与基于训练序列的均衡算法相比，CMA-LMS盲均衡算法在无线紫外光散射通信系统中的性能并不会下降过多。而改进后的间隔CMA-FSE算法的误码率曲线性能最好，不仅在同信噪比时的误码率最低，且在1~10 dB的小信噪比下误码率也能降低1~2个数量级。

在计算复杂度方面，由于乘法计算最为消耗时间，因此可以用乘法计算次数衡量算法复杂度。LMS每次迭代过程需要2次乘法计算，为均衡器抽头个数，所以当输入序列长度为时，算法的复杂度为2。RLS算法的矩阵运算较多，每次迭代过程需要6次乘法计算，因此算法的复杂度为6。因为间隔CMA-FSE算法可等效为个并行信道模型，所以它的计算复杂度是LMS算法的倍，即复杂度为，改进算法的复杂度与之相同。一般情况下，较小（即1<≤4）时就有较好的均衡效果，所以总体上改进后的间隔CMA-FSE算法的计算复杂度高于LMS算法，接近RLS算法。

4.2 改进CMA-FSE算法性能分析

首先验证当接收信号信噪比发生变化时算法的收敛情况，并对改进前后的算法进行对比分析，图7和图8为对比的结果。

对于改进前的CMA-FSE算法，从图7(a)可知，当步长尺度因子较大时，均方误差可以在迭代300次左右时就快速收敛，但在信噪比减小到7 dB时算法发散。图7(b)表明，当步长尺度因子较小时，虽然在小信噪比时也能收敛，但信噪比为20 dB时的收敛过程明显变慢，在迭代1 200多次时才趋于稳态。

从图8可以看出，改进算法不仅在大信噪比时收敛快，并且在小信噪比时也可以稳定地工作。另外还可以看出，算法处于稳态时的均方误差与信噪比有关，信噪比越小，稳态均方误差越大，且稳态均方误差的方差也更大。

图7 未改进CMA-FSE误差收敛曲线

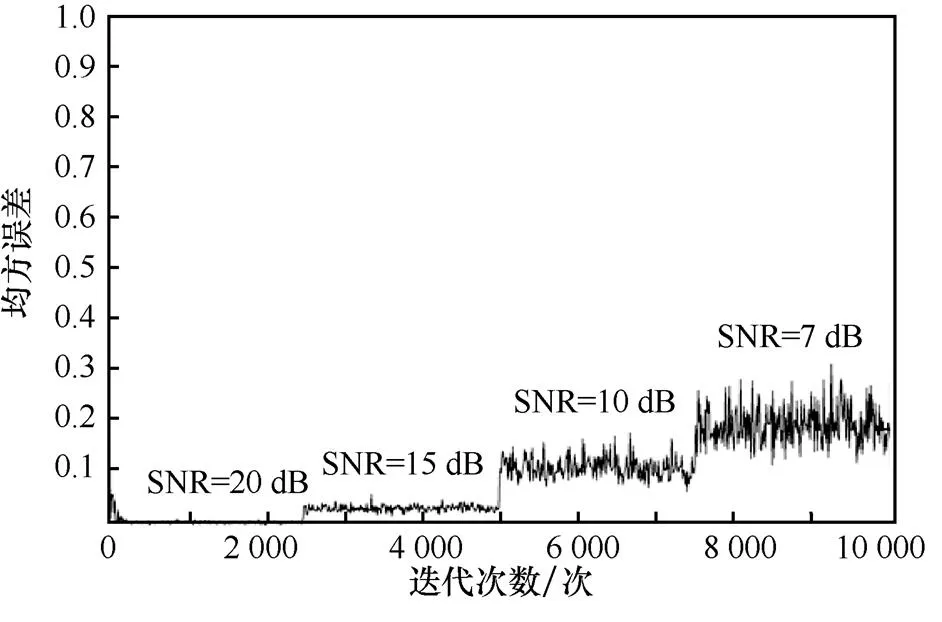
图8 改进后CMA-FSE误差收敛曲线

接下来，分析改进算法对信道变化的跟踪性能，表1中光束发散角和接收视场角不变，收发仰角由45○切换到60○，通信距离由100 m切换到200 m，同时信噪比由10 dB切换到15 dB，结果如图9所示。

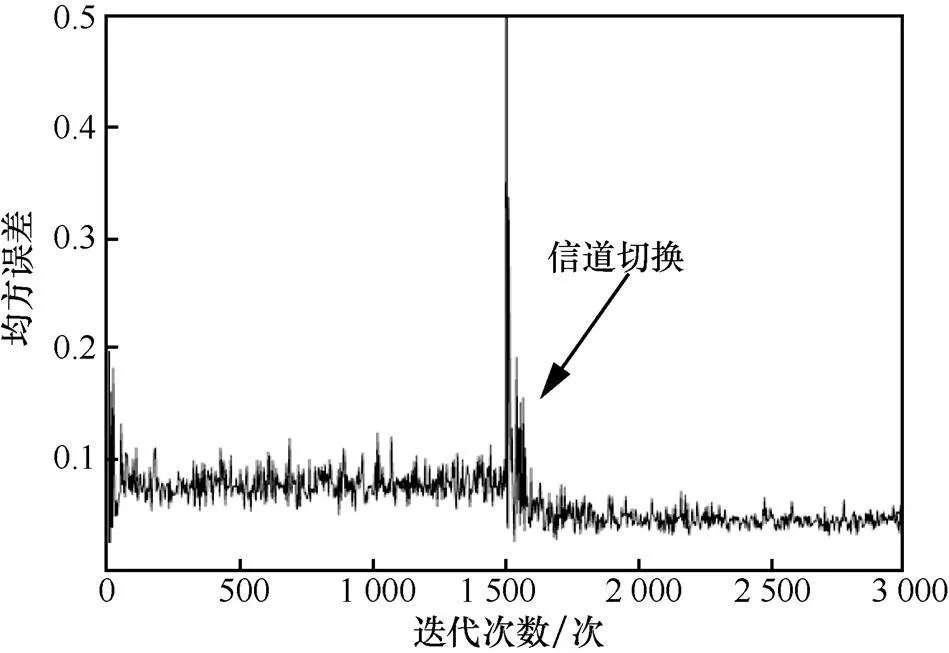
图9 改进CMA-FSE信道跟踪曲线

图9表明，改进CMA-FSE算法能快速跟踪信道的变化，当信道发生改变时，在不到500次的迭代后就能使均方误差收敛。虽然切换后的信道码间干扰更为严重，但最终的稳态均方误差却小于切换前的，这说明接收信号的信噪比对均衡器稳态误差的影响更大。

图10 改进CMA-FSE算法误码率曲线

图10表明，改进CMA-FSE算法能起到良好的均衡效果，在相同的信噪比下，采样间隔越小，误码率越低。这是因为FSE可以等效为匹配滤波器后接线性均衡器的系统，所以对于噪声有较好的抑制作用，且采样间隔越小，采样点越多，抑制作用越明显。

5 结束语

无线紫外光散射通信系统中的码间干扰严重，如果不采用有效的信道均衡算法，则会极大地限制通信带宽。本文采用了分数间隔均衡器对信道进行均衡，并利用信号的恒模特性使用CMA对分数间隔均衡器进行了盲实现。由于CMA-FSE算法的敛散性对接收信号的信噪比敏感，因此在步长计算公式中引入信噪比来保证算法收敛。在盲均衡算法中信噪比很难直接估计，在合理假设噪声功率为恒定值的情况下，以接收信号的均方值衡量信噪比的大小。仿真结果表明，改进CMA-FSE均衡算法能有效地改善输出信号误码率性能，并快速跟随信道变化和信噪比变化，在小信噪比下也有良好的均衡效果，可以提升无线紫外光散射通信系统的性能。

[1] 陈薛刚, 占光. 紫外光散射通信的军事应用研究[J]. 国防科技, 2010, 31(3): 24-27.CHEN X G, ZHAN G. A study of communication theory and its military application[J]. Nation Defense Science and Technology, 2010, 31(3): 24-27.

[2] LIAO L, DROST R J, LI Z, et al. Long-distance non-line-of-sight ultraviolet communication channel analysis: experimentation and modelling[J]. IET Optoelectronics, 2015, 9(5): 223-231.

[3] WANG L, HE Q, XU Z, et al. Performance of non-line-of-sight ultraviolet communication receiver in ISI channel[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2010, 7814(6): 781409-7.

[4] ZHANG S, ZHANG J, SO H C. Mean square deviation analysis of LMS and NLMS algori-thms with white reference inputs[J]. Signal Processing, 2017, 131: 20-26.

[5] AGAZZI O E, HUEDA M R, CARRER H S, et al. Maximum-likelihood sequence estimation in dispersive optical channels[J]. Journal of Lightwave Technology, 2005, 23(2): 749-763.

[6] SCARANO G, PETRONI A, BIAGI M, et al. Second order statistics driven LMS blind fracti-onally spaced channel equalization[J]. IEEE Signal Processing Letters, 2017, PP(99): 1.

[7] HATZINAKOS D, NIKIAS C L. Blind equalization using a tricepstrum-based algorithm[J]. IEEE Transactions on Communications, 1991, 39 (5): 669-682.

[8] 张贤达, 保铮. 通信信号处理[M]. 北京: 国防工业出版社, 2000.ZHANG X D, BAO Z. Signal processing for communications[M]. Beijing:National Defence Industrial Press, 2000.

[9] JOHANNISSON P , SJÖDIN M, KARLSSON M, et al. Modified constant modulus algorithm for polarization-switched QPSK[J]. Optics Express, 2011, 19(8): 7734-7741.

[10] LUETTGEN M R, REILLY D M, SHAPIRO J H. Non-line-of-sight single-scatter propagation model[J]. Journal of the Optical Society of America A, 1991, 8(12): 1964-1972.

[11] QIN H, ZUO Y, LI F, et al. Analytical link bandwidth model based square array reception for non-line-of-sight ultraviolet communication[J]. Optics Express, 2017, 25(19): 22693-22703.

[12] DING H, CHEN G, MAJUMDAR A K, et al. Modeling of non-line-of-sight ultraviolet scat-tering channels for communication[J]. IEEE Journal on Selected Areas in Communications, 2009, 27(9): 1535-1544.

[13] XU Z, CHEN G, ABOUGALALA F. Experimental performance evaluation of non-line-of-sight ultraviolet communication systems[J]. Colloids & Surfaces A Physicochemical & Engi-neering Aspects, 2008, 6709(s2-3): 161-173.

[14] 徐浩然, 左勇, 张文博, 等. 紫外光散射通信系统的噪声研究[J]. 光散射通信研究, 2013, 39(2): 65-69.XU H R, ZUO Y, ZHANG W B, et al. Research on noise in ultraviolet communication systems[J]. Study on Optical Communications, 2013, 39(2): 65-69.

[15] 赵太飞, 余叙叙, 包鹤, 等. 无线日盲紫外光测距定位方法[J]. 光学精密工程, 2017, 25(9): 23-24.ZHAO T F, YU X X, BAO H, et al. Ranging and positioning method using wireless solar blind ultraviolet[J]. Optics and Precision Engineering, 2017, 25(9): 23-24.

Improved CMA-FSE blind equalization algorithm for wireless ultraviolet communication

ZHAO Taifei1,2, LIU Longfei1, WANG Jing1, YANG Liyang1

1. Faculty of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, China 2. Robot Technology Used for Special Environment Key Laboratory of Sichuan Province, Southwest University of Science and Technology, Mianyang 621010, China

There are serious intersymbol interference (ISI) and signal attenuation in wireless ultraviolet communication system. Aiming at this problem, an improved constant modulus fractionally spaced equalizer (CMA-FSE) based on signal-to-noise (SNR) estimation was proposed. The algorithm combined the fractionally spaced equalizer (FSE) and constant modulus algorithm (CMA) for blind equalization of wireless ultraviolet channels. The input SNR was measured by the mean square value of the received signal, and it was used to determine the best iterative step to ensure the convergence of the equalization algorithm. Simulation results show that the improved CMA-FSE algorithm can converge rapidly under various SNR, and it can effectively suppress ISI and improve the BER performance of the system. Compared with the existing algorithms, the improved algorithm is more useful in channel tracking and noise suppression.

ultraviolet communication, intersymbol interference, channel equalization, signal-to-noise radio estimation

TN929.1

10.11959/j.issn.1000−436x.2019065

2018−04−28；

2018−09−20

国家自然科学基金−中国民航局民航联合研究基金资助项目（No.U1433110）；西安市碑林区科技计划基金资助项目（No.GX1617）；陕西省教育厅科研计划基金资助项目（No.17-JF024）；特殊环境机器人技术四川省重点实验室开放基金资助项目（No.17kftk04）

TheNatural Science Foundation of China−Civil Aviation Administration of China Joint Research Fund (No.U1433110), Science and Technology Planning Program Funded by Beilin District of Xi’an (No.GX1617), Scientific Research Program Funded by Shaanxi Provincial Education Department (No.17-JF024), Fund of Robot Technology Used for Special Environment Key Laboratory of Sichuan Province (No.17kftk04)

赵太飞（1978− ），男，河南浚县人，博士，西安理工大学教授，主要研究方向为紫外光散射通信技术、路由技术、网络抗毁性技术、物联网技术等。