基于Pignistic概率函数和相关系数的证据组合方法

2019-03-28杨晓萍廉伟健李孟杰钱志鸿

通信学报 2019年3期

杨晓萍，廉伟健，李孟杰，钱志鸿

杨晓萍，廉伟健，李孟杰，钱志鸿

（吉林大学通信工程学院，吉林长春 130012）

D-S证据理论不能很好地解决证据之间高冲突的情况，得到的结果与事实相悖，并且在实际的应用中无法解决“一票否决”的问题。针对上述不足，提出了一种基于Pignistic概率函数和相关系数的新证据冲突衡量标准（Pcor）和基于该标准的加权证据组合方法。该方法用Pcor来衡量证据间的冲突，通过建立支持矩阵来确定各证据的支持度，用加权平均法修正证据，使用Dempster组合规则，最终得出与事实相符的结果。数值算例表明，所提方法有效地解决了高冲突证据组合问题，与相关算法相比，具有更好的收敛性。

D-S证据理论；冲突衡量；相关系数；证据组合；信任度

1 引言

D-S证据理论（Dempster-Shafer evidence theory）作为多传感器信息融合决策层重要方法之一，具有良好的信息融合能力，所需要的条件比贝叶斯概率论更弱些，在不确定、不知道的情况下可以很好地解决问题，因此被广泛地应用于决策分析、信息融合[1-2]、模式识别[3]、目标识别等领域。然而在一些特殊的情况下，采用Dempster组合规则将信息源的信息进行组合，会产生与事实相悖的结论，从而使组合失去意义。国内外研究者认为这种情况是由证据之间高冲突引起的，并提出了大量的改进算法，主要分为2类：1) 针对证据理论本身组合存在的问题进行修改，有效地解决了证据之间的高冲突问题，参见文献[4-6]；2) 在经典理论算法的基础上，对存在冲突的证据进行预处理，也有效地解决了证据之间高冲突带来的问题，参见文献[7-8]。这些改进算法从多个方面丰富了Dempster组合规则，并推动了其发展，使其更加适合实际应用。

本文在第二类改进算法的基础上，借助Murthy[8]思想，在Pignistic概率函数[9-10]的基础上引入相关系数来确立冲突衡量标准，并根据此衡量标准确立各证据权重，使用加权平均思想降低冲突证据在组合中的影响，最后使用Dempster组合规则完成证据组合。

2 D-S的基本概念

D-S中，用表示识别框架，={1,2,…,θ}，其中，对象θ(1≤≤)是的一个子集，且是互不相容的元素。包含了所有对象，其幂集定义为2，是所有子集的集合。

定义1 基本概率赋值函数（BPA，basic probability assignment）[11]。设为识别框架，如果函数：2→[0,1]满足()=0、∑()=1，则称为上的基本概率赋值函数。其中，()叫作的基本概率赋值，也就是对的支持度，为空集。如果∀⊆且满足()>0，则称为焦元。将框架内给出的(1)、(2)、…、(2)用行向量表示，=[(1),(2),…,(2)]。

Dempster组合规则表达式为

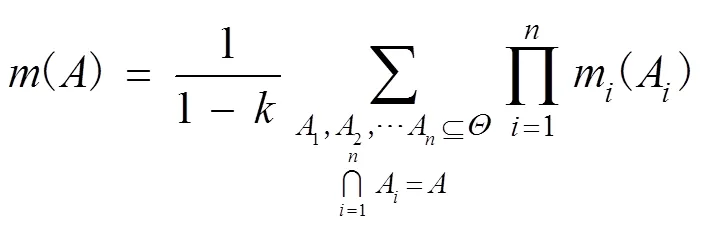
其中，∈[0,1)表示证据之间的冲突程度，计算式如式(2)所示。

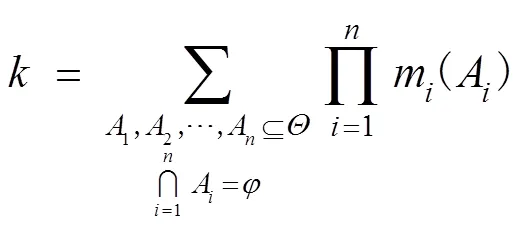
3 证据冲突方法分析

在证据理论中，证据冲突[12]产生的原因主要有2个：1) 因不可抗力（如人为的放射干扰、雷电等恶劣天气）引发传感器收集到的证据与事实存在较大的偏差；2) 因人们对事物认知程度造成证据冲突即辨别框架不全面，导致各传感器给出的报告相互之间冲突较高。因此，冲突衡量标准要有高冲突证据筛选的能力。

3.1 经典的证据衡量方法

经典的证据衡量方法在衡量证据之间的关系时存在一些有悖于事实的情况，通过例1来对经典的证据衡量方法进行分析。

例1 设识别框架={1,2,3,4}，3个证据的BPA分别为

1：1(1)=1(2)=0.5

2：2(1)=2(2)=0.5

3：3(3)=3(4)=0.5

1) 冲突系数

其中，A、B作为证据1、2的焦元表示符合识别框架的所有子集。

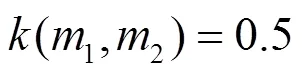
2) Joussemle距离

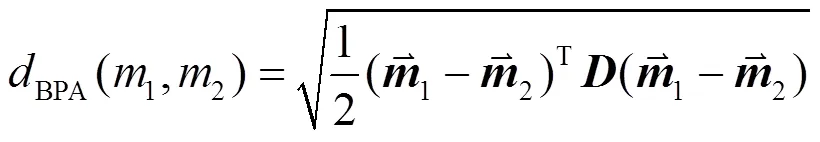
例1中的1与3是2个完全冲突的证据，根据完全冲突的意义来说，证据间求得的BPA值应无限接近于1，但是使用式(4)计算求得BPA=0.707，因此使用Joussemle距离也存在与事实相悖的情况。

3) 相关系数

相关系数的计算式如式(5)所示。

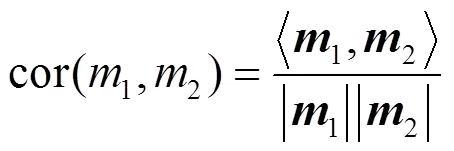
可以看出，经典的证据冲突方法在某些情况下会出现问题。

3.2 新的证据冲突衡量标准

针对相关系数无法在证据中包含非单子集的情况下正确地判断出冲突程度，加入Pignistic概率函数，解决相关系数在此方面的不足。

定义2 Pignistic概率函数。设()为识别框架下的基本概率赋值函数，则Pignistic概率函数为

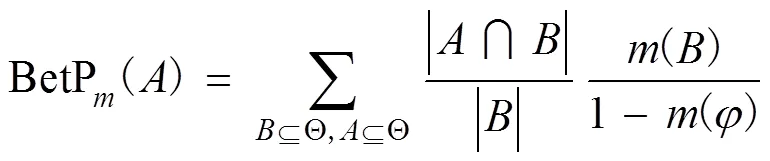
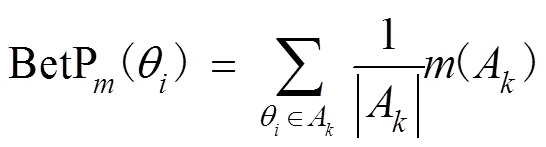
那么在识别框架下，证据经过Pignistic概率函数转化后如式(8)所示。

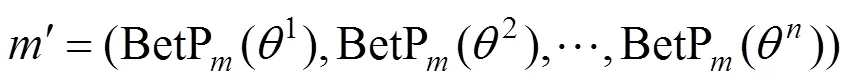
定义4 设2个证据的单子集Pignistic概率函数为1、2，引入相关系数思想，来表示1、2证据之间的冲突程度，用表示，

从式(9)很容易看出∈(0,1)，这不仅保留了相关系数的能力，还解决了相关系数在非单子集情况下能力不足的问题。下文的例2是文献[11]中的具体事例，用来说明在衡量证据冲突方面具有的优势。

例2 设识别框架={1,2,3,…,20}，2个证据的BPA分别为如下所示。

1：1(2,3,4)=0.05,1(7)=0.05,1()=0.1,1()=0.8

2：2(1,2,3,4,5)=1

其中，的变化规律为{1}，{1,2}，{1,2,3}，…，{1,2,3,…,20}。表1给出当变化时，新的证据冲突程度与文献[12]中采用的证据距离BPA和文献[11]中定义的关联系数的对比。

从表1可以看出，当1()变化到{1,2,3,4,5}时，1()与2(1,2,3,4,5)的焦元相同，此时，2个证据间的冲突是最小的，但随着的变化证据冲突=0.05是不变的，说明不能用来衡量证据间的冲突程度。观察证据距离BPA、关系系数和本文提出的冲突程度都是随着的变化而变化，因此也可以作为证据冲突衡量标准，该新的证据冲突衡量标准简称为Pcor。表1中的数据表明：证据距离BPA与冲突程度呈正比关系；关系系数的值越大，证据间的冲突程度越小，证据间相似度就越高；的变化趋势与关系系数相似。显然，和与BPA的变化趋势相反。为了直观地表达各冲突程度变量的变化趋势，图1绘出了表1中BPA、1−、1−随着包含元素个数变化的曲线。

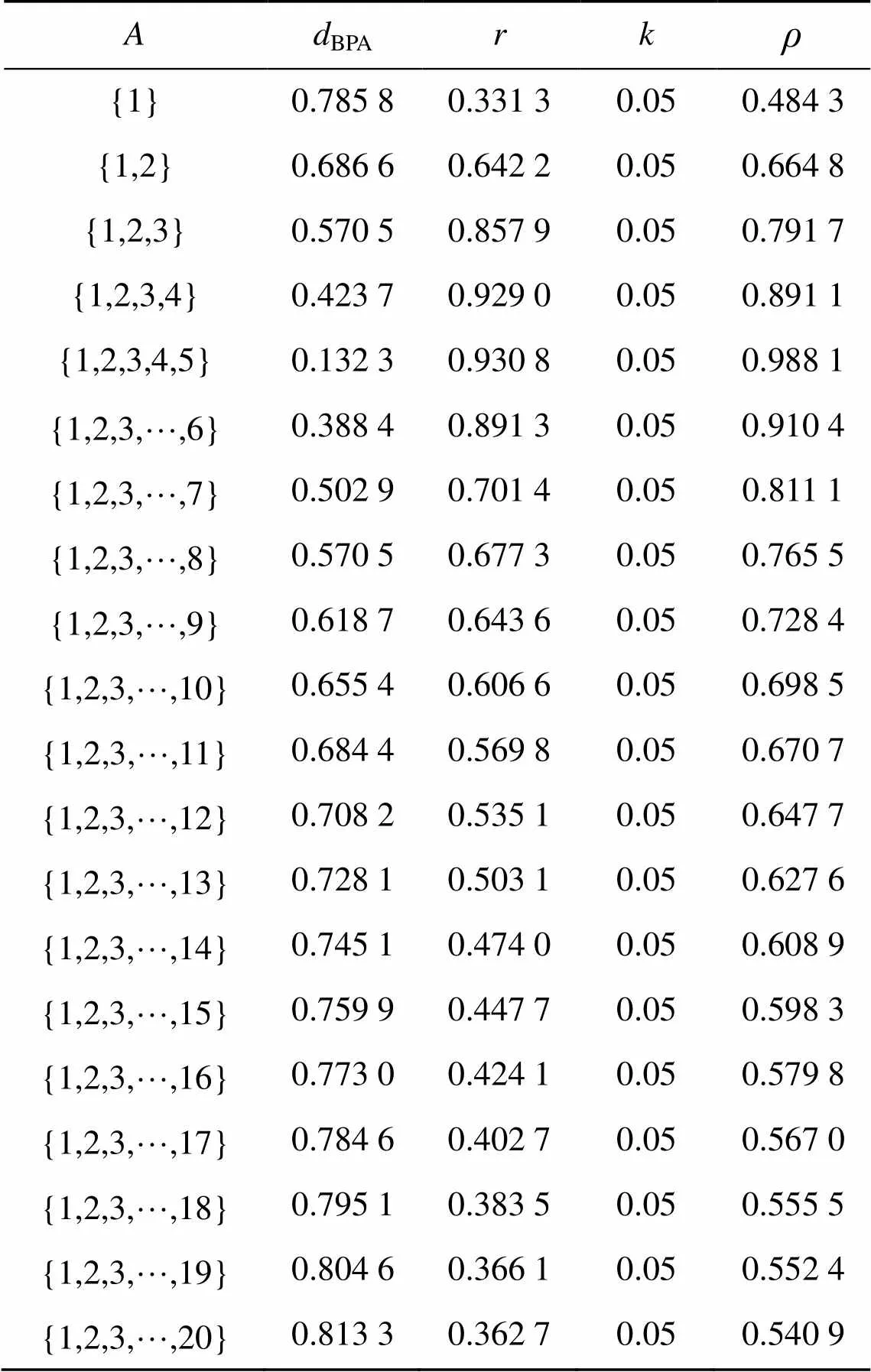
表1 各证据冲突衡量标准之间的比较

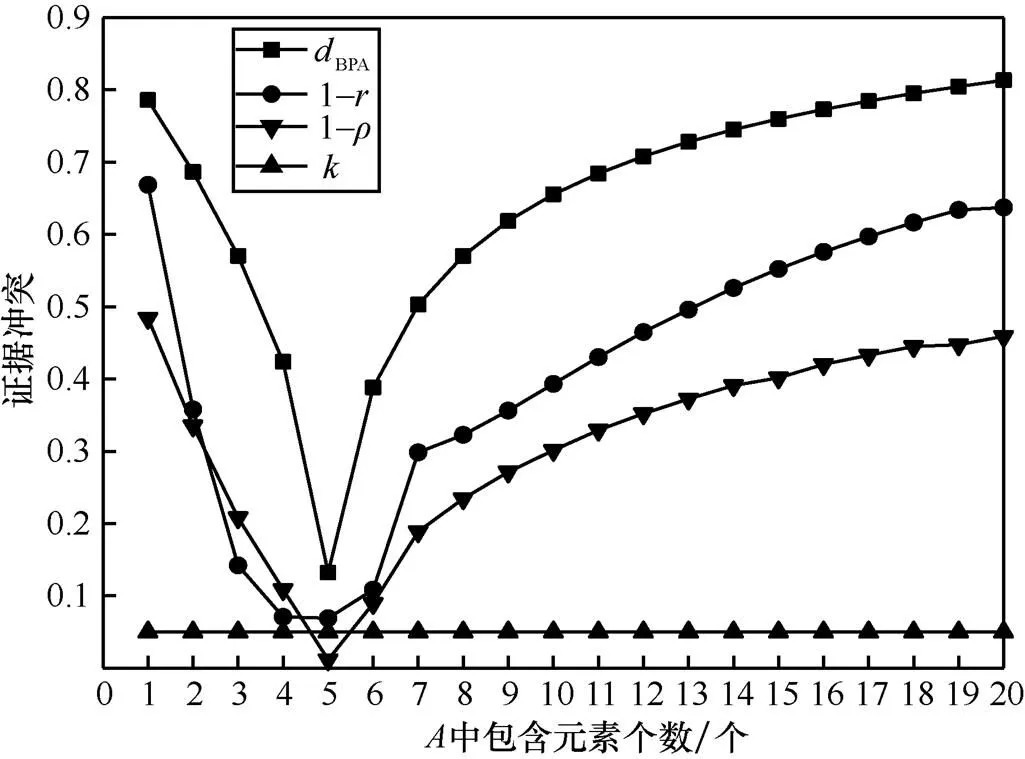
图1 证据冲突衡量标准的比较

从图1可以看出，BPA、1、1−有着相同的变化趋势，在变化到{1,2,3,4,5}时，BPA、1、1−的值都降到最小，并且随着的进一步增加，三者数值都随着冲突程度变大而相应地升高，这与客观实际情况相吻合。从变化的趋势来看，1−变化趋势更加平滑。从以上的分析可以得出，本文定义的证据冲突衡量标准Pcor可以准确全面地描述证据间的冲突程度。

4 基于Pcor的加权证据组合方法

在传感器决策信息融合领域，一直都秉承着少数服从多数的原则[13-15]，Zadeh[16]认为在Dempster组合规则下组合结果与事实相违背的原因是某个证据或少数证据不相容，但是对这些少数的证据我们无法规避或清除。为了能使大多数的证据决策保留下来，在证据合成过程中，降低一个或少数不相容证据的权重，Pcor是一个有效的方法，其利用值确定各证据的权重系数[17-18]，最后利用加权平均的思想进一步弱化不相容证据。

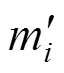
步骤1 根据式(7)与式(9)计算任意2个证据间的值并根据构建支持矩阵SM，如式(10)所示。

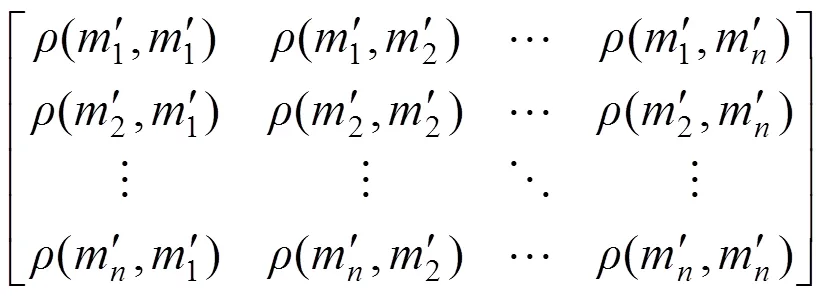
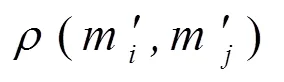
步骤2 计算m的支持度Sup(m)为

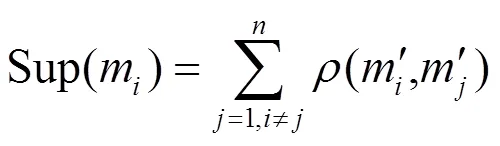
步骤3 计算m的权重ω为

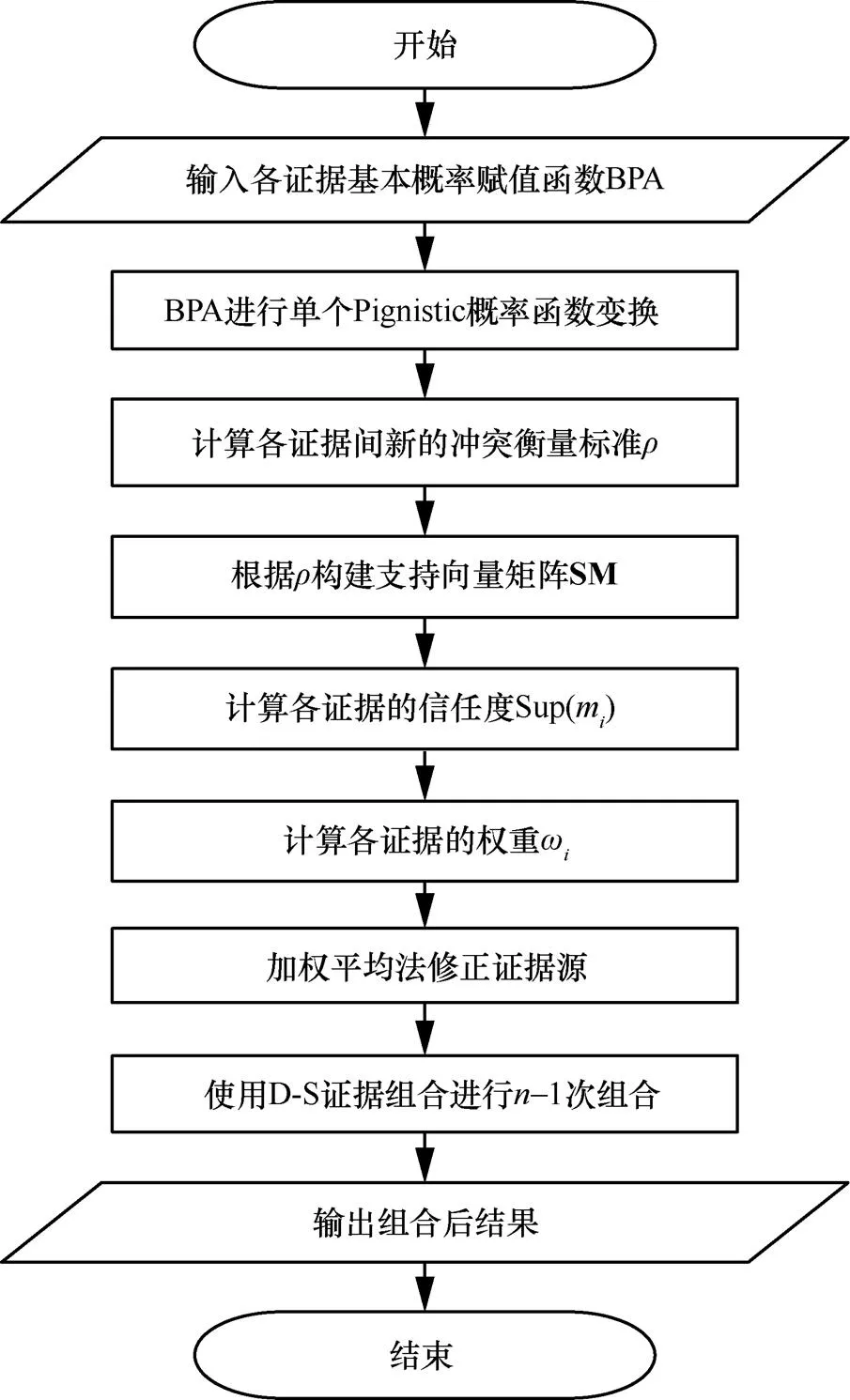
图2 基于Pcor的加权证据组合方法流程

5 仿真算例与分析

通过具体事例，将一些典型的组合规则与本文提出的组合方法进行对比分析，说明本文方法能较好地解决高冲突组合问题。

例3 设某一识别框架为={，，}，有5个传感器的BPA分配分别如下所示。

1()=0.5，1()=0.2，1()=0.3

2()=0.0，2()=0.8，2()=0.2

3()=0.6，3()=0.3，3()=0.1

4()=0.55，4()=0.25，4()=0.2

5()=0.65，5()=0.15，5()=0.2

从5个传感器给出的证据看出，1、3、4、5证据认为发生的可能性较大；证据2对的支持度较高，相比较而言，证据2是一条高冲突证据。通过6种组合规则对例3证据进行组合，其结果如表2所示。

从表2可以看出，由于2()=0，Dempster组合规则无法在更多证据支持的情况下得出一个合理的数值，组合后()值始终为0，显然根据原始的Dempster组合规则做出的决策是不符合常理的；Yager组合规则分析出Dempster组合规则存在的问题并进行了相应的改进，把冲突的部分分配给未知项，随着证据的增加，组合后的()逐渐变大，但()值仍为0，Yager组合规则虽然提高了组合理论分配的合理性，但是仍没有解决Dempster组合规则处理高冲突证据带来决策错误的问题；孙全等[20]对Yager组合规则进行了改进，很好地克服了该规则一直以来对的否定，随着加入组合的证据增多，()值也在增加，只是收敛速度较慢，当第5个证据加入组合时，()=0.236 9、()=0.506 7，结果不确定性依然存在，仍不利于决策；Murthy方法很好地解决了高冲突问题，当第5个证据加入组合后，()=0.809 0，可以准确地做出决策判断，但是Murthy组合规则只是对证据间进行了简单的平均，并没有考虑证据之间的相关性与差异，在2()=0.8这一基本概率赋值的干扰下，()与()的组合结果相差较大。

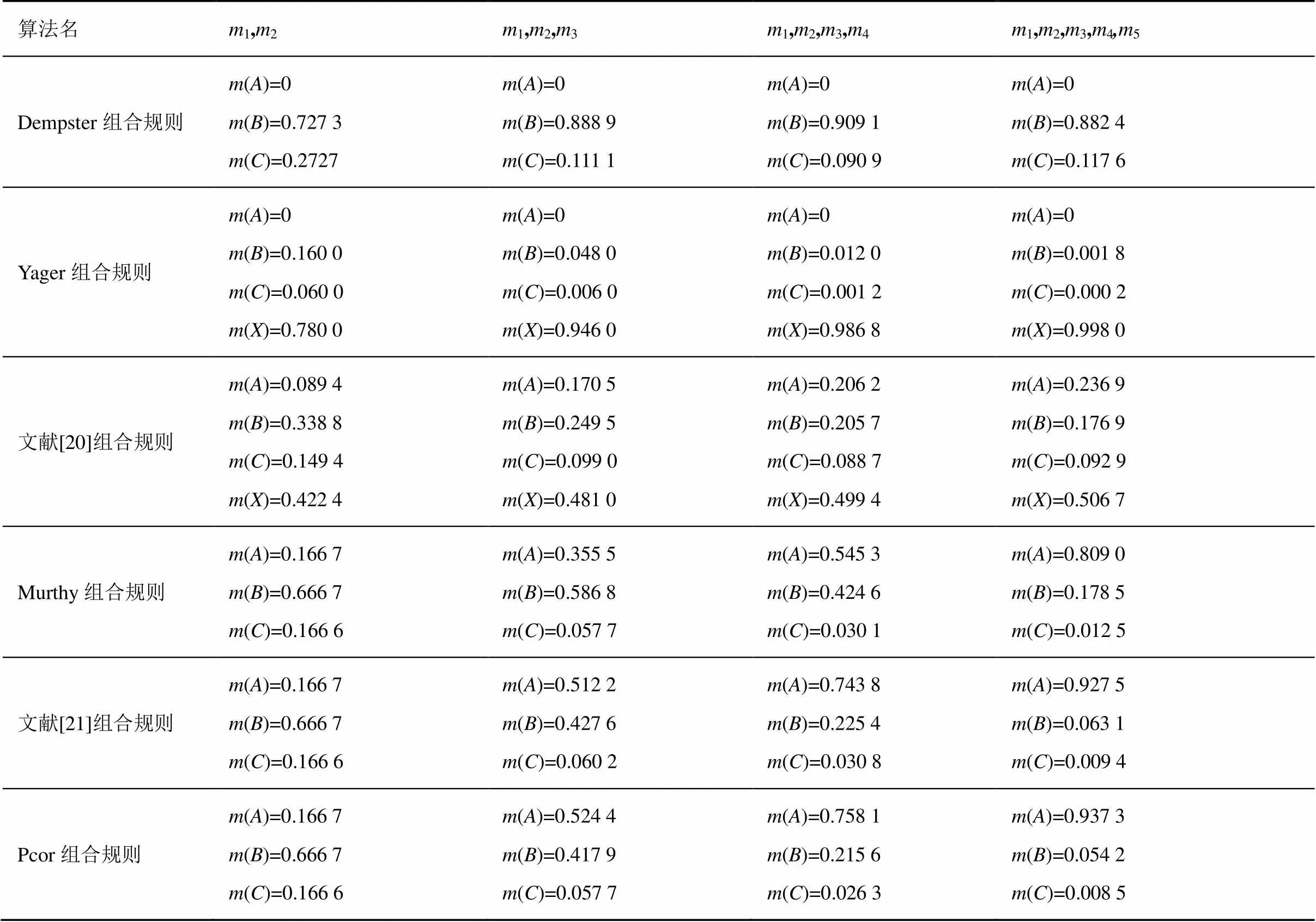
表2 6种组合规则结果比较

Pcor组合规则，不仅选取了Murthy组合规则中的组合优点，还利用新的证据冲突衡量标准Pcor来确定证据间的权重系数，达到对证据的合理分配。如表2所示，按照Pcor组合规则组合后，各元素满足客观规律()>()>()，对比Murthy组合规则明显缩小()与()组合结果的差异。随着对支持度高的证据加入，Pcor组合规则中()组合结果越来越大。当第4个和第5个证据加入时，()值分别为0.758 1、0.937 3，比Murthy组合规则中的()=0.545 3、()=0.809 0有明显提高，那么Pcor组合规则更加利于决策。对比文献[21]的组合方法，两者在组合效果上都非常不错，但是在相同的条件下，Pcor组合方法的()值是较大的，对最终的判断结果更有利。如图3所示（由于Dempster组合规则与Yager组合规则()值一直为0，2条线与横轴重合），Pcor组合规则在第3个证据加入组合时()数值就很高，这得益于该规则分配权重的合理性，有效地降低证据2在整个组合过程中的影响，随着证据4、5加入，证据2的影响越来越小。因此Pcor组合规则不仅提高了证据组合的可能性，还很好地反映了实际的组合过程，符合实际情况。

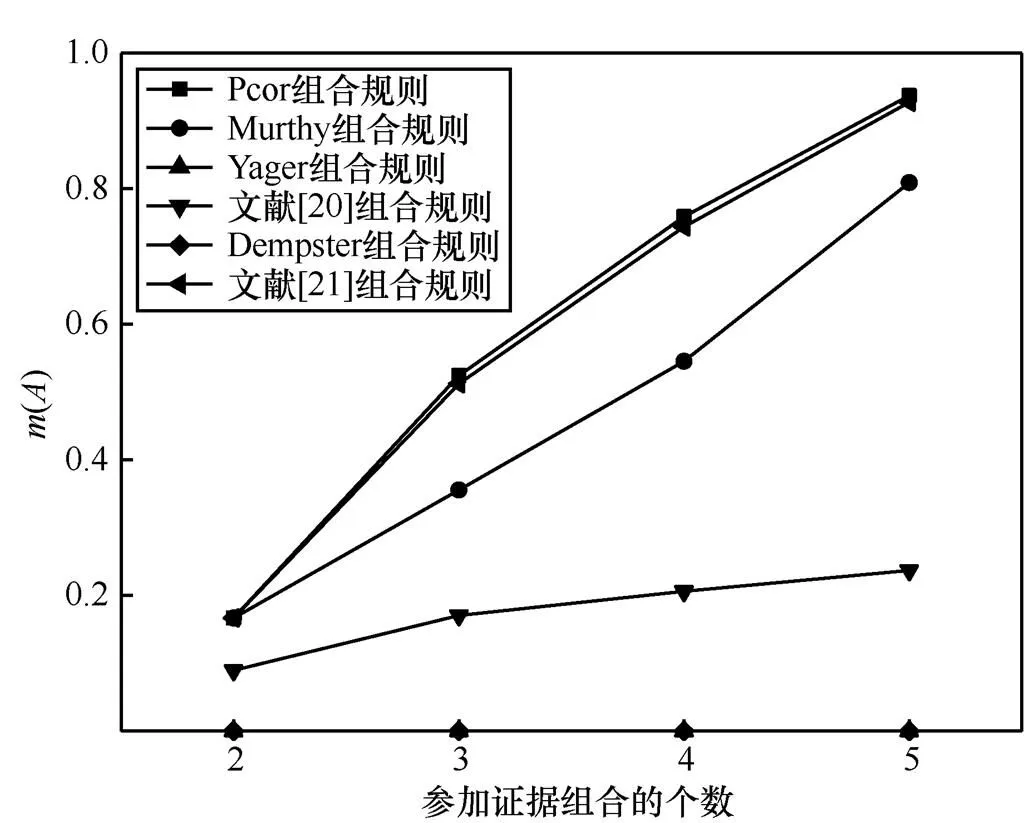
图3 不同组合规则m(A)的收敛性

6 结束语

采用经典证据理论对高冲突证据进行组合时，会产生与事实相悖的结论。本文结合Pignistic概率函数变换与相关系数确立新冲突衡量标准Pcor，在理论与事例两方面验证Pcor可以有效地衡量证据间的冲突，并且根据Pcor提出了有效的组合规则。算法事例表明，本文提出的Pcor组合规则全面结合了证据间的相关性与差异，最大程度降低了高冲突证据带来的组合问题，不仅加快了组合结果的收敛速度，降低了决策风险，还提高了抗干扰能力和证据高冲突时决策的准确性。

[1] DEMPSTER A P. Upper and lower probabilities induced by a multi-valued mapping[J]. Annals Mathematical Statistical, 1967, 38: 325-339.

[2] SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.

[3] 雷蕾, 王晓丹, 邢雅琼, 等. 结合SVM 和DS 证据理论的多极化HRRP 分类研究[J]. 控制与决策,2013,28(6): 861-866.LEI L,WANG X D, XING Y Q, et al. Multi-polarized HRRP classification by SVM and DS evidence theory[J]. Conctol and Decision,2013, 28(6): 861-866.

[4] LEFEVRE E, COLOT O, VANNOORENBERGHE P. Belief function combination and conflict management[J]. Information Fusion, 2002, 3(2): 149-162.

[5] YAGER R R. On the Dempster-Shafer framework and new combination rules[J]. Information Sciences,1987,41(5):93-138.

[6] HAN D Q, DENG Y, HAN C Z. Weighted evidence combination based on distance of evidence and uncertainty measure[J]. J Infrared Millim Waves, 2011, 30(5): 396-400.

[7] LIU Z G, DEZERT J, PAN Q, et al. Combination of sources of evidence with different discounting factors based on a new dissimilarity measure[J]. Decision Support Systems, 2011,52(1): 133-141.

[8] MURPHY C K. Combining belief functions when evidence conflicts[J]. Decision Support Systems, 2000, 29(1):1-9.

[9] 宋京伟, 王晓丹, 宋亚飞, 等. 基于幂Pignistic概率距离的加权证据组合方法[J]. 电子学报, 2018,39(1):117-125.SONG J W,WANG X D,SONG Y F, et al. Weighted evidence combination method based on power-Pignistic probability distance[J]. Journal on Communications, 2018,39(1):117-125.

[10] 肖建于, 童敏明, 朱昌杰, 等. 基于Pignistic概率距离的改进证据组合规则[J]. 上海交通大学学报,2012,46(4):636-645.XIAO J Y,TONG M M,ZHU C J,et al. Improved combination rule of evidence based on Pignistic probability distance[J]. Journal of Shanghai Jiaotong University, 2012,46(4):636-645.

[11] 邓勇, 王栋, 李齐, 等. 一种新的证据冲突分析方法[J].控制理论与应用,2011,28(6):839-844.DENG Y, WANG D, LI Q, et al. A new method to analyze evidence conflict[J]. Control Theory & Applications, 2011, 28(6): 839-844.

[12] JOUSSELME A L,GRENIER D,BOSSE E. A new distance between two bodies of evidence[J]. Information Fusion, 2001(2):91-101.

[13] 毕文豪, 张安, 李冲. 基于新的证据冲突衡量的加权证据融合方法[J]. 控制与决策,2016,31(1):73-78.BI W H, ZHANG A, LI C. Weighted evidence combination method based on new evidence conflict measurement approach[J].Control and Decision, 2016,31(1):73-78.

[14] 孟光磊, 龚光红. 证据源权重的计算及其在证据融合中的应用[J]. 北京航空航天大学学报, 2010, 36(11): 1365-1368.MENG G L, GONG G H. Weight co-efficients calculation for evidence sources and its application in evidences fusion[J]. Journal of Beijing University of Aeronautics and Astronautics,2010,36(11): 1365-1368.

[15] LIU Z G, PAN Q, DEZERT J, et al. Classification of uncertain and based on evidence theory[J]. Neurocomputing, 2014,133(8): 459-470.

[16] ZADEH L. A simple view of the Dempster-Shafer theory of evidence and its implication for the rule of combination[J]. AI Magazine, 1986, 7(2): 85-90.

[17] 刘准钆, 程咏梅. 基于证据距离和矛盾因子的加权证据合成法[J]. 控制理论与应用,2009,26(12):1439-1442.LIU H G, CHENG Y M. Combination of weighted belief functions based on evidence distance and conflicting belie[J]. Control Theory and Applications, 2009,26(12):1439-1442.

[18] 蒋雯, 吴翠翠, 贾佳, 等. D-S证据理论中的基本概率赋值转换概率方法研究[J]. 西北工业大学学报,2013,31(2):295-299.JIANG W, WU C C, JIA J, et al. A probabilistic transformation of basic probability assignment(BPA) in D-S evidence theory[J]. Journal of Northwestern Polytechnical University, 2013, 31(2): 295-299.

[19] 宋亚飞, 王晓丹, 雷蕾, 等. 基于相关系数的证据冲突度量方法[J]. 通信学报, 2014, 35(5): 95-100.SONG Y F, WANG X D, LEI L, et al. Measurement of evidence conflict based on correlation coefficient[J]. Journal on Communications, 2014, 35(5): 95-100.

[20] 孙全, 叶秀清, 顾伟康. 一种新的基于证据理论的合成公式[J]. 电子学报, 2000, 28(8): 117-119.SUN Q, YE X Q, GU W K. A new combination rules of evidence theory[J]. ACTA Electronica Sinica, 2000,28(8):117-119.

[21] 邓勇, 施文康, 朱振福. 一种有效处理冲突证据的组合方法[J]. 红外与毫米波学报,2004,23(1):27-32. DENG Y, SHI W K, ZHU Z F. Efficient combination approach of conflict evidence [J]. J Infrared Millim Waves,2004,23(1):27-32.

Evidence combination method based on Pignistic function transformation and correlation coefficient

YANG Xiaoping, LIAN Weijian, LI Mengjie, QIAN Zhihong

College of Communication Engineering, Jilin University, Changchun 130012, China

The situation of high conflict between evidences and one ballot veto cannot be solved by classical D-S rule, and the results obtained from classical D-S rule are contrary to the facts. To solve this problem, a new standard to measure conflicts between evidences was proposed based on the combination of Pignistic function transformation and correlation coefficient, and also a novel kind of weighted combination method which was applied to measure conflicts between evidences was put forward according to the standard. After that, a support matrix was constructed based from which the credibility of evidence was obtained, and the weighted average method was used to revise the evidence. Finally, the combination was accomplished by using Dempster’s rule. The result of numerical examples shows that it’s effective to solve the combination of conflicting evidence. Compared with other methods, the proposed method has good astringency.

D-S evidence theory, conflict measure, correlation coefficient, evidence combination, credibility

TP391

10.11959/j.issn.1000−436x.2019049

2018−04−23；

2018−08−22

吉林省校共建计划专项基金资助项目（No.SXGJQY2017-9）；吉林大学高层次科技创新团队建设基金资助项目（No.2017TD-19）；国家自然科学基金资助项目（No.61771219）；吉林省科技厅重点科技研究发展基金资助项目（No.20180201081SF）

The Special Fund Project of Jilin Province School Co-Construction Plan (No.SXGJQY2017-9), The High-Level Technology Innovation Team Building Project of Jilin University (No.2017TD-19), The National Natural Science Foundation of China (No.61771219), The Science and Technology Research Development Fund of Jilin Provincial Science and Technology Agency (No.20180201081SF)

杨晓萍（1963− ），女，黑龙江鹤岗人，博士，吉林大学教授、硕士生导师，主要研究方向为网络通信传输技术和多传感器数据融合技术。