基于公有验证和私有验证的数据持有性验证方案

田俊峰，柴梦佳，齐鎏岭



基于公有验证和私有验证的数据持有性验证方案

田俊峰1,2，柴梦佳1,2，齐鎏岭1,2

（1. 河北大学网络空间安全与计算机学院，河北 保定 071002；2. 河北省高可信信息系统重点实验室，河北 保定 071002）

越来越多的用户愿意把数据存储在云存储系统中，数据安全是云存储系统面临的关键问题，为了保证存储在云中数据的完整性、有效性，数据持有性验证（PDP）就显得尤为重要。为了验证云存储服务提供商是否完整地存储了用户的数据，基于不可否认PDP（NRPDP）方案提出了一种新的数据持有性验证方案。该方案基于公有验证和私有验证，可以同时对云存储中服务提供商与用户的可信性进行验证，满足了验证的不可否认性。理论证明了该方案的不可否认性，实验验证了各阶段运行时间效率比现有的单一的公有验证方法或私有验证方法更优。

云存储；不可否认；数据持有；公有验证；私有验证

1 引言

云计算被广泛地应用于不同领域，企业根据需求访问云中的计算机和存储系统，将资源切换到需要的应用。云存储的出现为用户数据的存储和访问提供了方便，它在云计算的基础上集合了网络中多种类型的存储设备，对外存储提供数据存储和业务访问服务[1]。随着数据规模逐渐变大，对存储能力的需求急剧增加，大量资源可存储在云端，用户可以通过相关设备登录到云上，根据需要使用云设备对数据进行存取和访问[2]。

然而云服务提供商是不能被完全信任的[3]。近几年，多次出现云存储数据丢失以及攻击者通过攻击云存储系统来盗取用户数据的安全问题，这使云服务提供商的可靠性引起了人们的关注[4]。2012年，谷歌Gmail邮箱爆发数据丢失问题，约15万用户数据被删除；2014年，苹果“iCloud泄密事件”导致22万用户的账号密码信息泄露。用户一旦选择将数据存储在云中，就失去了对它的管理能力，无法确定该数据文件的完整性，进而将面临巨大的安全风险。因此，高效、正确地对云存储中数据进行完整性验证值得人们关注。

在数据完整性验证中，有不可信云服务器的存在，也有不诚实用户的存在。有些用户为追求利益，会否认正确验证结果，否认云服务器对数据进行的合法操作，其最终目的是得到非法经济补偿。因此，同时验证用户和服务器的可信性是非常有必要的。为此，有多种数据持有性验证[5-6]（PDP, provable data possession）和数据可恢复性证明[7-8]（POR, proof of retrievability）方案被提出。

本文采用私有验证和公有验证相结合的方式对云中的数据进行验证，并对验证结果进行不可否认验证，通过2种算法输出的结果对，判定云中存储的数据完整性。

2 相关工作

2.1 基于公有验证的数据持有性验证方案

Ateniese等[9]在CSS（ACM Conference on Computer and Communications Security）上首次提出了数据持有性证明，并且为了提高验证效率，利用RSA方案构造了同态验证标签（HVT, homomorphic verifiable tag），省去了对整篇文章的检索和下载，确保文章内容不被验证方了解。他们首次将“挑战−应答”协议引入完整性验证中，这样进行验证的次数便可不受限制，可根据需要进行多次数据完整性验证。该模型主要针对静态数据存储。Dan等[10]同样提出了一种具有同态特性的PDP机制，其基于BLS签名，不仅有效地减少了验证过程中的通信开销，而且极大地节省了数据存储空间。在验证过程中，使用第三方审计角色（TPA, third-party audits）代替用户对数据进行持有性验证工作。Wang等[11]首次详细地介绍了公有验证模型，提出了一种支持动态操作的基于Merkle Tree的数据持有性证明方案，该方案支持数据修改、插入、删除等更新操作。Wang等[12]将可信第三方（TTP, trusted third party）引入数据持有性方案中，在实行公开验证的同时，实现了对数据隐私的保护。第三方可直接对存储在云中的数据进行数据持有性验证而不需要通过用户进行验证，很好地保护了验证内容的隐私性。但TTP的假设条件过于理想化，实现困难，并且会有额外的开销。

2.2 基于私有验证的数据持有性验证方案

私有验证具有验证速度快的优点，Curtmola等[13]针对云中数据存储具有多副本的特性，实现了针对多副本的MR-PDP（multiple-replica PDP）方案，它能有效地对所有副本数据进行完整性认证，且验证开销起伏不明显。Wang等[14]提出一种不可否认PDP（NRPDP, non- repudiable PDP）方案，该方案基于私有验证方法，不仅可以验证客户端与服务器的可信性，而且可以验证另一方的可信性。

2.3 基于混合验证的数据持有性验证方案

绝大多数的验证方案基于单一的验证方法，而Hanser等[15]提出了基于公有验证和私有验证的PDP协议，在满足了高效性和便捷性的同时，通过基于ECC（elliptic curve cryptography）的验证方法，在2种验证过程中均使用一致的元数据，达到了节省计算开销的效果。但此方案仅关注了云服务商的可信性，未考虑到恶意用户的存在，忽略了用户存在欺骗行为。

近年来，PDP方案仍是一个研究热点，但是大部分局限于单一的私有验证或公有验证，具有较大的局限性，虽然对服务器的可信性进行了很好的验证，但是忽略了用户是否可信的研究。

本文提出了支持私有验证和公有验证的数据持有性验证方案（PPPDP, provable data possession scheme based on public verification and private verification），在数据持有验证过程中采用2种验证方式，通过2种验证输出的结果对，对文件的完整性进行判定。

3 预备知识

3.1 ECC加密算法

ECC加密[16]是一种基于公钥体制的加密算法，它具有安全性高、存储空间占用小和运算速率高的特点。ECC密码体制研究的数学基础是椭圆曲线，通常由韦尔斯特拉方程定义。椭圆曲线上所有的点和椭圆曲线外一个被称为无穷远点的特殊点的集合连同一个定义的加法算法一起构成Abel群。

由=++…+=的特性可得，如果(，)和这2个参数是已知的，则可求出点(，)的值。但若想通过点、求出的值，理论上是不可能的。

基于椭圆曲线的反向不可求解的特性，EIGamal密码体制过程有如下表述。

1) 首先通过设定椭圆曲线的参数，选定一条椭圆曲线，并得到E(，)，将待加密信息嵌入曲线上得到点P，再对点P做加密交换。

2) 取E(，)的一个生成元，E(,)和作为公开参数。

3) 用户A选择作为密钥，=作为公开钥。此时，若用户B存在向A发送消息P的需求，用户B需随机选取某正整数，将其代入之前选定好的椭圆曲线，得到以下生成点对C={，P+}，即为密文。

4) A解密时，使密文点对中的第二个点减去用自己的密钥与第一个点的倍乘，即P+−=P+()−=P。

已知C的信息，若攻击者求得P，那么的值必须为已知的。而的值只能通过已知的和经过离散对数计算求得，而非已知，因此，P不可得。

3.2 同态验证标签

同态可验证标签的概念由Ateniese等[9]提出。同态标签具有同态性，一般利用其同态性来对云中存储的数据进行完整性验证。同态标签具有以下2个特性：1) 由于只需对少量特定的数据块进行数据持有性验证，极大程度上降低了通信开销和计算成本；2) 已知任意2个数据块m和m，则m+m的标签信息(m+m)可以很容易地由它们各自的标签信息(m)与(m)生成，即(m+m)=(m)(m)。

文件块的验证元数据由标签信息构成，服务器同时存储着文件和相应的标签信息，具有不可伪造的特性。

3.3 COM函数

目前，存在2种承诺方案，针对全功能发送方的标准承诺方案与针对全功能接收方的完美承诺方案。但是，承诺方案并不能同时保证信息理论上隐藏和绑定。因为云可以被视为一个强大的接收者，所以本文使用了Pedersen COM函数[17]进行公有验证，并对此COM函数进行如下参数设置。

离散对数函数G是素数阶的群，使和是G的元素，则很难通过计算求解loghmod的值。

Pedersen COM函数过程如下：取Z，从Z随机选择辅助值构造一个关于的承诺函数COM(,)，使COM(,)=ghmod。存在定理已证明COM(,)不显示关于的信息[18]。

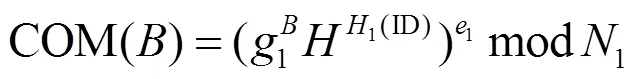
4 方案设计

目前，企业和个人都倾向于借助云存储来实现对大量隐私数据的存取。现有的数据持有性验证证明都只考虑了云服务提供商的可信性，而没有考虑到恶意用户的存在。在现实生活中，由于利益的驱使，恶意用户是真实存在的。因此在对云中数据进行持有验证时，需要同时对云服务提供商和云用户的可信性进行验证。虽然已有研究提出了基于公有验证、私有验证以及混合验证的模型，但都是针对云服务提供商进行可信性验证，并没有考虑用户的可信性。由于公有验证和私有验证存在不同的特点，因此本文基于2种验证方法提出了新的数据持有性验证方案——PPPDP，通过2种验证方法并行，充分考虑到云服务提供商和云用户可信性的验证工作。

4.1 整体框架

该模型涉及云租户或客户端（client）、云服务提供商（CSP, cloud service provider）、验证者（verifier）3种角色。三者之间的关系如图1所示。

图1 角色关系

本方案主要涉及3种角色，其分别负责不同的功能，具体介绍如下。

1) 客户端，即用户。客户端由于持有大量数据需要存储，而本地存储空间有限，因此选择将数据存放在云存储服务器中。为了更好地验证云服务器中数据的完整性，若用户存在数据完整性验证需求，则指派验证者代其验证。

2) 云服务提供商。云服务提供商在云中为个人和企业提供云存储服务。在本文中，云服务提供商是不可信的，因此它将接受数据完整性证明中的挑战，以验证其可信性。

3) 验证者。验证者主要负责云中数据完整性的验证工作，代替用户进行验证操作，在得到用户授权之后，及时对挑战请求进行响应。

数据持有性方案流程如图2所示。

4.1.1 公有验证

公有验证能有效地避免用户的否认。本文中的公有验证方式采用任意验证者根据运行COM函数产生的值对文件进行完整性验证，可以很好地保证验证的公开性。公开验证的结果会对最终的数据持有性证明的结果产生影响，既验证客户端的可靠性又验证服务器端的可靠性。文中私有验证和公有验证使用同样的元数据，减少了数据的存储量，从而有效地提高了验证速度。

4.1.2 私有验证

私有验证方案是由数据拥有者对存储在云中的数据进行验证。当验证者获取私钥时，采用私有验证的方式对存储在云中的数据进行验证，在验证的过程中存在着较少的标量乘法运算，可以节省大量的时间和空间，减少存储开销和计算开销，并且在验证过程中不需要学习任何关于数据存储的问题，只需要利用私钥对存储在云中的数据进行验证。

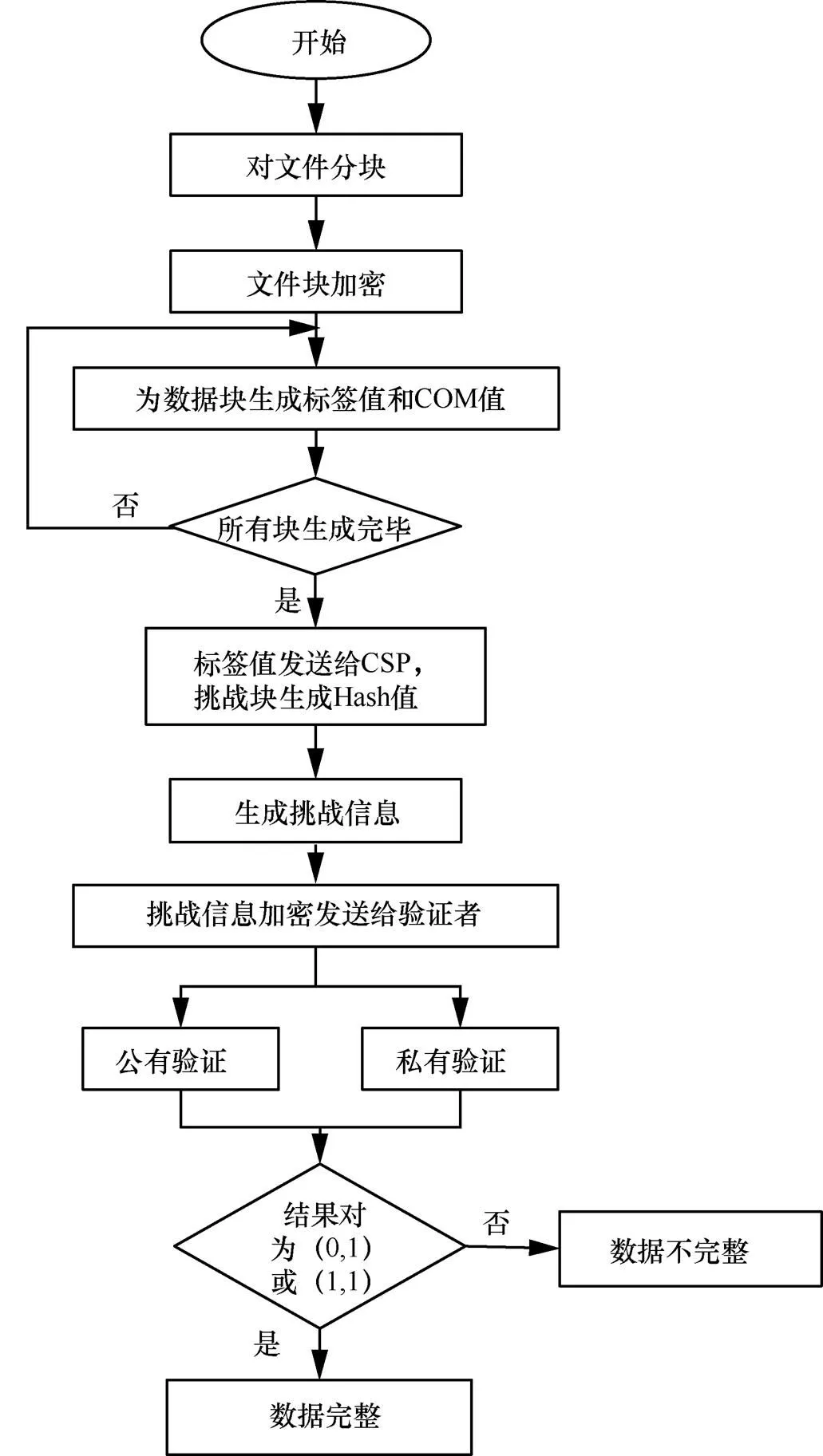
图2 数据持有性方案流程

4.2 基本定义

PPPDP方案主要由5个多项式时间算法构成，分别为KeyGen、Prepare、ProofGen、VerifyProof和VerifyCOM。

KeyGen(1)。此密钥生成算法由客户端运行。算法输入安全参数，利用概率算法进行计算，求得公有密钥p与私有密钥sk。

Prepare(sk，pk，m,)→({{1},{2},…,{M}}，COM)。此标签生成算法由客户端运行，主要用于生成验证所需要的元数据tag和证据，算法输入为公钥pk、私钥sk和原文件，输出文件经过分块、加密生成数据块的tag和运行COM函数生成值COM。

VerifyProof(sk，pk，chal，)→{1，0}。此验证证据算法由验证者运行，根据返回的数值判断文件块是否完整。算法输入公钥pk、私钥sk、挑战信息chal和证据，输出固定的数值表示数据块是否被完整持有。

VerifyCOM({}，{}，，{COM})→{1，0}。此算法为公开验证算法，任何人均可运行，主要功能是用于验证存储在云中的数据是否完整。算法输入所选块{}和对应的COM {COM}的索引，输出{COM}是否通过验证，同时确定验证者的可信性。

PPPDP方案主要由3个阶段组成，分别为预处理阶段、挑战阶段和私有验证与公共COM验证阶段。各个阶段的主要流程介绍如下。

1) 预处理阶段

用户Y运行KeyGen和Prepare算法，在本地存储(pk，sk)。用户Y给服务器S发送私钥pk、文件、COM值和标签，并把这些信息从本地存储中删除。

2) 挑战阶段

用户Y通过运行相应的算法生成挑战信息chal，并发送给服务器S。服务器S把挑战信息chal作为输入运行ProofGen算法，并生成相关证据，发送给用户Y。

3) 私有验证与公共COM验证阶段

用户运行VerifyProof算法来对证据进行检测，通过返回值确定云中的数据是否完整。服务器可以向公众公开部分COM，任何人可以根据公开的COM运行VerifyCOM，验证数据是否完整地存储在云中，即验证用户的可信性。

4.3 验证流程

4.3.1 预处理

为了更好地对存储在云中数据进行完整性、正确性的验证，在持有性验证之前要对文件进行预处理操作。预处理操作主要是对文件进行分块，验证采用抽样的方式，避免了对大量数据块的验证，只需要使用少量的数据信息来完成对整个文件的验证工作。选定要验证的在云中存储的文件之后，首先对文件进行分块处理，把整个文件等分为个数据块，每个文件块m(0<≤)中含有bit数据，若最后一个数据块不足bit，则使用0进行补位。分块结束后，对每一个数据块进行加密操作，确保文件块的信息不被泄露。其中每个数据块都具有唯一标识符参数id。每个数据块m都能得到位数据，用表示第块数据的元数据。把块数据分为组，=，为用户选择的随机参数，为保证为整数，若不满足被整除，则用0补齐数据块，其中，数据块<>=(m,1,…,m)。

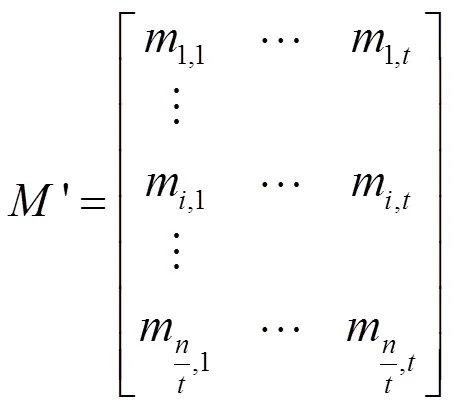
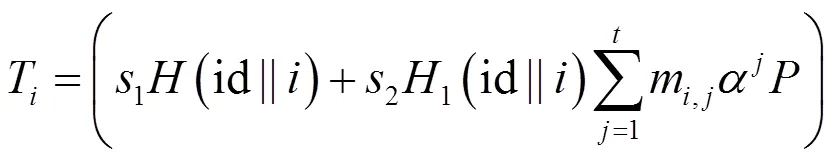
利用同态验证标签对文件中的数据块生成数据标签tag，输出文件集合和标签集合{<>，<>},0<≤。同时为每一个文件块(0<≤)运行COM函数，利用COM函数生成不可否认验证需要的信息COM，计算方法如式(2)所示。

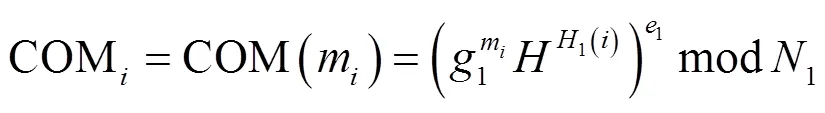
计算出每一个文件块的标签和COM之后，输出(m,,{T，COM}1)信息，为防止覆盖存储着相同信息的不同块，每个数据块都与生成的标签值和COM值绑定。把文件的信息（块标识符id）与生成的标签值和COM值一同存储在服务器上，删除客户端文件数据。

4.3.2 挑战阶段

在挑战阶段，客户端请求拥有块的证明，为保证安全性，挑战信息采用密文进行传输，数据持有者选取一条椭圆曲线(F)，并选取椭圆上的一点作为基点′，数据拥有者选择一个私有临时密钥′，并生成临时公开密钥′=′′，数据拥有者将(F)和′、′传给验证者，验证者收到数据持有者传送的消息后，将数据块M对应的检验信息、私钥和该数据存储时生成的标签2一起编码到()上的一点′，产生一个随机整数′，验证者通过计算产生2个数据1′=′+′′和2′=′′，再将1′和2′传送给数据拥有者。

1′−′2′=′+′′−′(′′)′+′′−′(′′)=′

数据持有者通过上述计算得到验证者挑战信息码′，再将′进行解码便得到验证者发送的挑战信息，即数据块m的挑战信息和2。验证者挑战信息发送成功。

4.3.3 验证阶段

分层多代理的结构能有效地避免单点故障，防止由于某个验证者的不可用造成整个验证系统的崩溃。多代理的验证采用主从结构的设计，主节点负责任务的分发、监控和节点切换；从节点的工作比较单一，只负责验证工作。利用文件块的访问粒度和用户访问的文件数对文件块进行分层。通过主节点对验证信息进行分配，验证的工作主要由从节点进行，主要的验证过程如下。

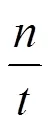
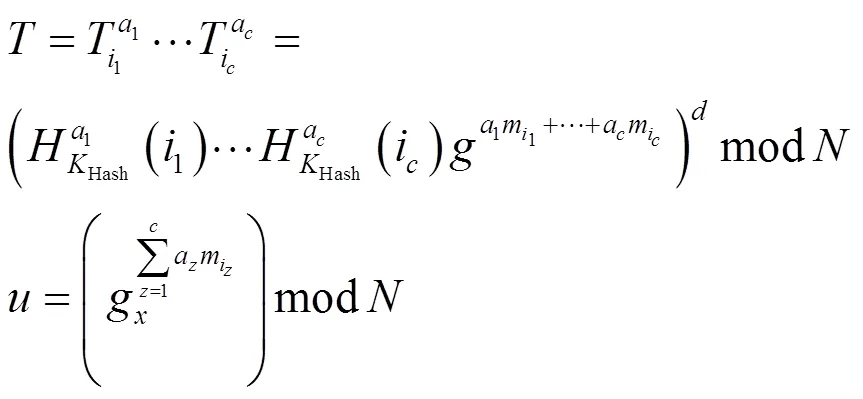
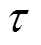
1) 令sk=(，，Hash)，chal的值为chal=(，1，2，g)。

2) 分别计算抽样块的索引值和相关系数，通过相关运算与客户端生成的证明进行比较，对于0<≤，计算抽样块的索引为I=1()；计算相关系数为a=f2()。

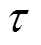
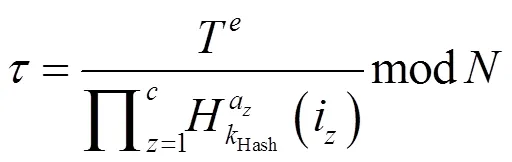
VerifCOM({m}，{}，，{COM})→{1，0}。在COM验证阶段，服务器可以请求所有被挑战的块，并且公开这些块和相关的COM。可采用VerifCOM函数来同时验证客户端和验证者的可靠性，令pk=(1，1，1，)；服务器可以请求错误块索引，并公开相关的COM信息和相关的数据块，如式(5)所示。

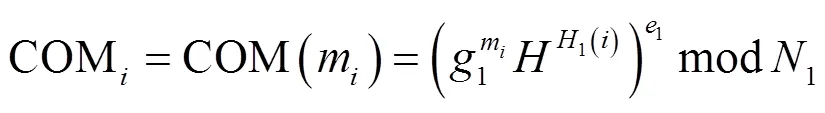
对所有要验证的块进行验证，验证者可以检查每个数据块的COM的有效性，为了防止服务器修改和伪造这些COM信息，可以采用加密的方式存储这些信息，任何人都可以基于公共信息计算s和t的值，并检查它们是否相等。

验证过程如下。

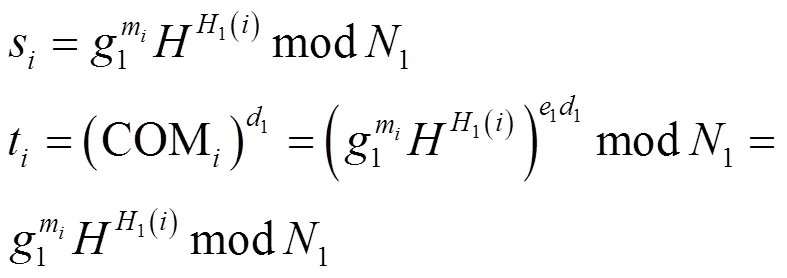
如果s=t，则说明块m和它生成的COM函数是一致的，当数据块和该数据块的COM值完全匹配时输出1，否则输出0。

在运行的过程中，VerifProof与VerifCOM是同时进行的，如果验证者不拥有私钥，在进行VerifProof运算时默认输出为0。2个运算生成结果对，如果结果对为(1, 1)，则证明数据完整且客户端可信；如果结果对为(0，0)或(1，0)则证明数据不完整。如果结果对为(0, 1)，则证明数据完整，客户端不可信。结果对用表示，如式(7)所示。

5 安全性分析

5.1 安全模型

为了达到更好的验证效果，使用数据持有性游戏和不可否认性游戏来定义此安全模型。

游戏1 数据持有性游戏

设置：挑战者运行KeyGen(1)产生密钥对(pk，sk)，保持sk值的隐私性，公开pk的值。

挑战：挑战者通过算法生成一个挑战信息chal并向敌手请求生成文件块m1，…，m(1≤≤)的持有性证明。

伪造：敌手根据挑战信息chal通过算法计算生成一个持有性证明，并把此证明发送给挑战者。

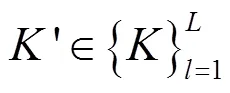
显然，敌手获得胜利的概率近似接近于抽取器抽取出挑战chal所对应文件块的概率。

游戏2 不可否认性游戏

设置：敌手通过运行KeyGen(1)，输出相同长度的数据对0、1。

挑战：挑战者运行Prepare (pk，sk，i，)→({{1},{2},…,{M}},COM)，输出0、1，其中COM(0)=0，COM(1)=1。选取随机数，{1,0}，把b、pk告知敌手。

结果：敌手运行VerifProof (pk，b)→{0,1}，如果b是m块的COM值则输出1，否则输出0。

5.2 安全性分析

定理1 假设是安全的伪随机函数，则本方案是在标准模型下支持数据持有性和不可否认性的方案。

证明

1) 数据持有性

在证明数据持有性时，使用伪随机函数和随机数分别在现实环境和理想环境中执行。

① 现实环境

设置：挑战者运行KeyGen(1λ)算法得到公钥pk和私钥sk，并保持其隐私性。

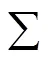
挑战：挑战者通过算法产生一个挑战信息chal并向敌手请求文件块m1,…,m(1≤≤)的持有性证明。

伪造：敌手根据挑战chal计算生成一个持有性证明，并把此证明发送给挑战者。

② 理想环境

使用随机数代替伪随机函数，则=[1，…，r]T。记录所有的随机数，并且在验证过程中使用相应的随机数进行计算。

假设敌手可以在发生改变的情况下完成验证，即在理想环境下，敌手成功找到′，使′=A1+−1。

由于和为随机生成的密钥，为纯随机数，则不等式如式(8)所示。

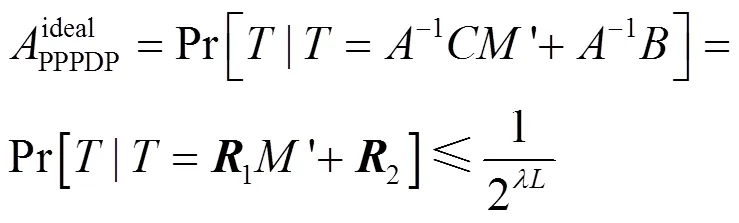
其中，1、2为随机数矩阵。

2) 不可抵抗性

利用还原法证明PPPDP方案的不可否认性。

假设存在敌手*，并且敌手赢了PPPDP方案的不可否认性游戏。可以构建一个验证者来打破COM验证。

设置：敌手运行KeyGen(1)，输出相同长度的数据对0、1。敌手把0、1的值发送给验证者。

挑战：验证者运行Prepare(pk, sk,m,)→({{1},{2},…,{M}},COM)，输出0、1，其中，(0)=0，COM(1)=1。

验证者选取随机数，→{1,0}。把b、pk告知敌手。

伪造：敌手运行VerifCOM(pk，)→{1,0}，输出结果1或0。

若概率表达式为

或

则验证者胜利。

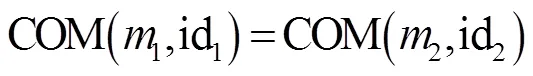
6 实验结果及分析

实验环境基于河北省高可信信息系统重点实验室的YF-TCI云平台进行搭建。本次实验使用YF-TCI平台中的3个服务器，并且部署OpenStack Ocata，云平台中每个虚拟机节点都运行Ubuntu 14.04.3 LTS，虚拟机节点的配置为CPU 4个核心，8 GB内存，200 GB硬盘空间，存储用户数据。算法使用的密码学库是版本1.0.2l的OpenSSL。实验结果存在随机性，因此对所有实验结果都进行了多次测试，取平均值作为最终结果。

PPPDP对S-PDP进行了改进，但是抽样方法与S-PDP是相同的。要想至少有一个被改动或被删除的文件块被抽中的概率不低于99%，经过计算，要检测的文件块数量至少为460个[14]。

6.1 COM函数的生成和验证

在PPPDP方案中，为了实现不可否认性，在预处理阶段对每一个数据块都要通过COM函数生成唯一对应的COM值，COM的值是一次计算可重复多次使用的。数据块分别为128 KB、64 KB、16 KB、4 KB时，运行COM函数生成COM值的时间与文件大小的关系如图3所示。从图3可以看出，COM值的生成时间与文件的大小呈线性相关。当数据块大小一定时，随着文件的增大，其对应的COM数量增加，计算时间会变长。当文件大小一定时，数据块增大，则数据块的数量减少，在一定程度上也会减少COM的生成时间。

图3 执行COM函数的时间

COM的验证时间如图4所示。当块大小固定时，验证时间变动不大。随着数据块逐渐变大，计算负担也随之增加，验证的时间成本增加，因此验证时间与数据块的大小相关。

6.2 PPPDP方案与PDP、POR方案的比较

表1 PPPDP方案与PDP、POR方案的性能比较

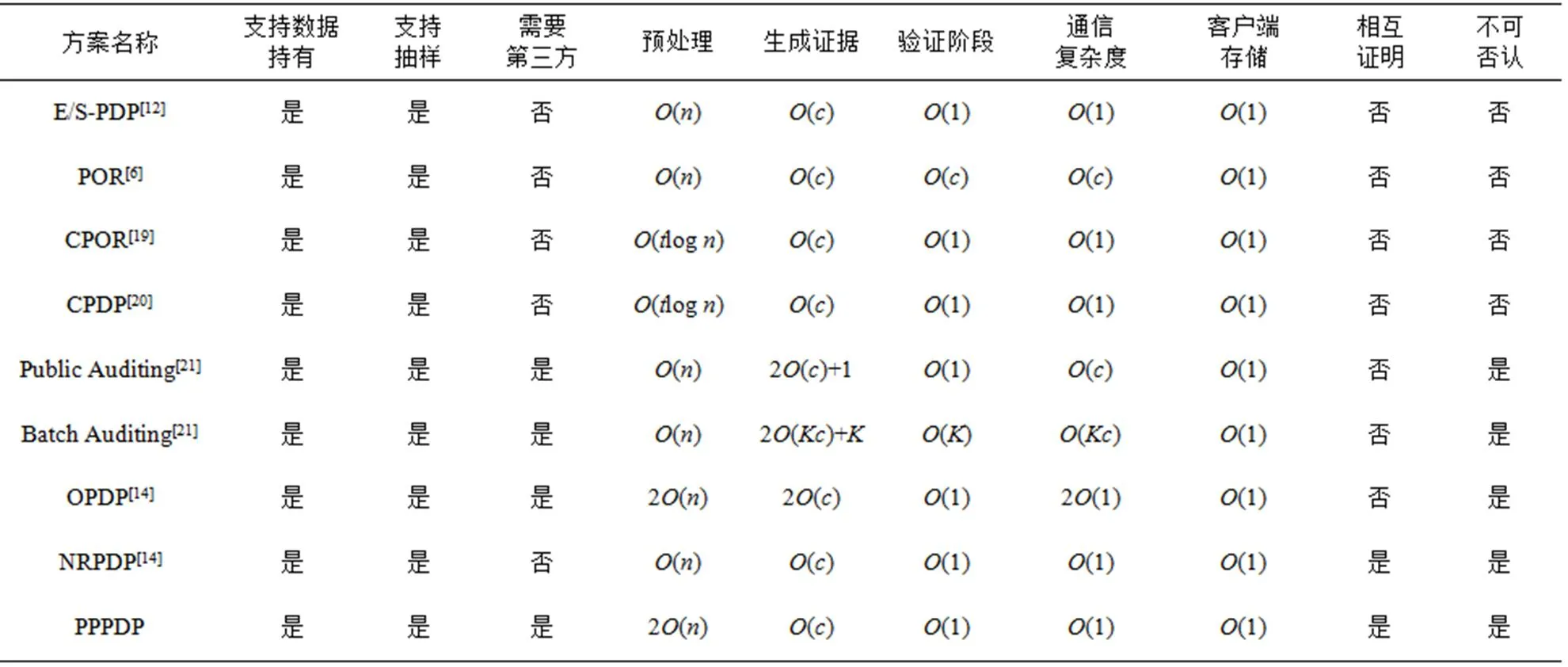
将基于2种验证方法的不可否认的PPPDP方案与已有PDP方案（S-PDP、CPDP、NRPDP等）和POR方案（POR、CPOR等）进行比较。对上述方案是否需要第三方、各个阶段的时间复杂度和通信存储复杂度等性能进行了对比，如表1所示。PPPDP方案在预处理、生成证据、验证阶段与其他方案相比有类似的时间复杂度和通信开销，能很好地实现不可否认性并满足客户端和验证者相互证明。

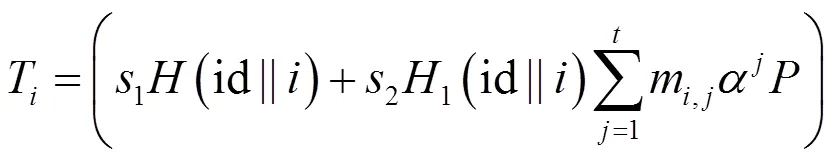
PPPDP方案与NRPDP方案在挑战验证阶段、数据存储阶段的时空复杂度是一致的，但是NRPDP方案只单独局限于私有验证，具有一定的局限性，而PPPDP方案可以采用2种验证方式并行进行验证。

6.3 PPPDP方案的效率测试

在预处理阶段和挑战验证阶段，将PPPDP方案与S-PDP、文献[15]中的PDP方案进行了对比，结果如图5~图7所示。在整个验证过程中，时间花费最多的阶段是预处理阶段，在挑战验证阶段需要的时间开销比较小。在预处理阶段，随着划分数据块的增大，运行时间逐渐减少，在相同块大小的情况下，运行时间随文件大小变化呈线性分布。在挑战验证阶段，这3种方案具有相似的操作，运行时间相似，大部分运行时间是I/O操作的时间，去掉I/O操作后，挑战时间接近恒定时间。

首先分析预处理阶段的时间开销。预处理阶段主要工作是客户端生成用于验证的元数据。在该阶段，实验需要测量3种方案生成密钥和验证标签的时间，主要包括生成密钥时间、I/O的时间以及将数据存储到磁盘的时间。其中，生成密钥的时间相对较少，主要耗时是指数计算所需要的时间。图5表示预处理阶段时间与文件大小之间的关系。由于3种验证方案都是对每个块执行求幂操作，预处理的时间随着文件大小的增加呈线性增长。PPPDP方案在预处理阶段时间开销比文献[15]中的PDP方案与S-PDP方案有所增加，这是因为PPPDP方案在此阶段会生成标签值和COM值，生成这些数据都会有一定的时间消耗。其中生成COM的时间开销小于生成标签值的时间开销，而且COM值只需计算一次就可多次利用，在验证较大数据块的完整性时，生成COM值的时间相对较小。

图5 预处理阶段

其次，考虑在挑战验证阶段产生的时间开销。PPPDP方案在此阶段主要工作包括客户端生成挑战chal，并将其发送到服务器上，服务器生成拥有chal的文件块证明之后，客户端验证服务器给出的拥有证明，并对公开的数据块COM值进行验证。这3种方案均挑战验证阶段，通过实验，对3种方案的挑战验证时间开销进行了对比。PPPDP方案、S-PDP方案与文献[15]中的PDP方案在挑战验证阶段具有类似的操作，文献[15]中的PDP方案在验证过程中需要决定用哪种验证方法进行验证，PPPDP方案在验证过程中采用2种验证方法并行的方式进行验证，提高了验证的效率，PPPDP方案与文献[15]中的PDP方案的时间开销相差不大。S-PDP方案需要相对较多的时间开销。如图6所示，3种方案的时间开销都随着文件大小的增加线性增加。

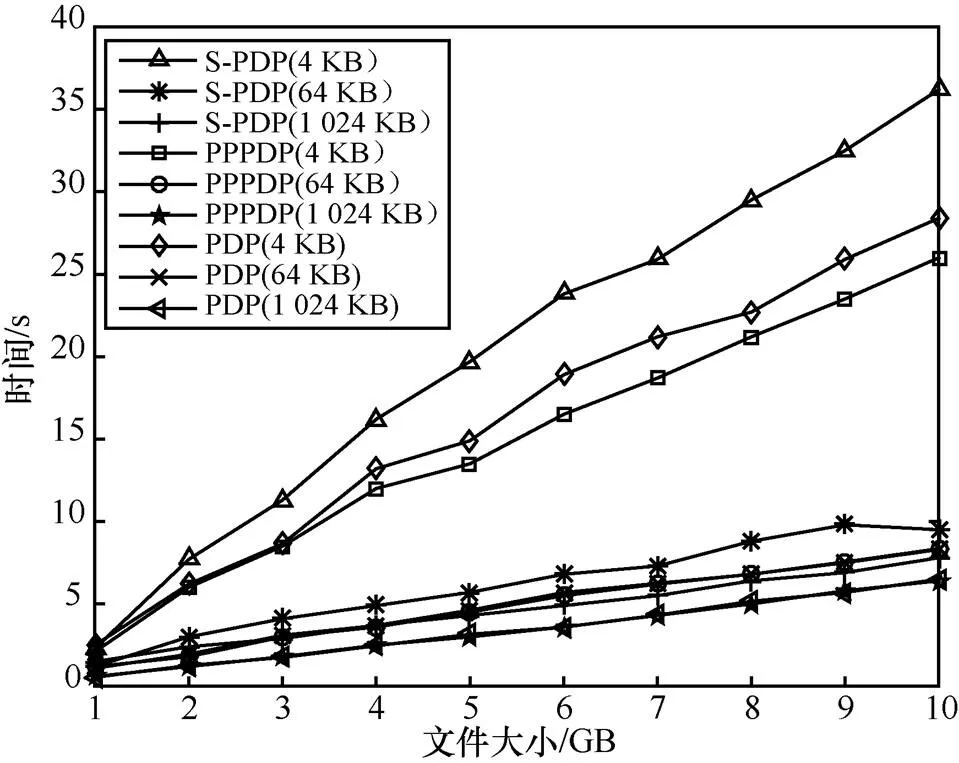
图6 挑战验证阶段

由于随着文件大小的增加，检索、读取和加载数据的时间随之增加，这些数据的操作统称为I/O成本。显然，当文件块的数量增加时，I/O成本增加。在对比过程中去掉I/O成本，再对3种方案进行对比。在去掉I/O成本之后挑战验证阶段的时间开销如图7所示，生成与验证证据的时间接近恒定时间。由于PPPDP方案采用并行的方法，比S-PDP方案与文献[15]中的PDP方案在时间成本上有所减少，说明PPPDP方案在挑战验证阶段具有一定的优势。

6.4 应用

PPPDP方案已作为一个相对独立的模块应用在某健康数据私有存储云管理信息系统中，该系统私有云的配置如下：软件平台采用OpenStack（CentOS 7 1511版本），硬件平台采用由5台大唐高鸿可信服务器（E5 2670 CPU，32 GB内存，3 TB硬盘）构成的集群作为云存储服务提供方环境，其中一台为NameNode，主要负责集群的控制和调度，另外4台为DataNode，主要负责数据存储和计算。

图7 去掉I/O的挑战验证阶段

PPPDP方案分为3种模块，客户端模块部署在客户机上，验证模块部署在审计端，服务端模块部署在NameNode上。对该信息系统进行数据持有性验证模块的操作。当对后台某个文件中数据块进行删除后，客户端对此文件进行数据持有性验证请求，验证者对此块进行验证。

经过一年多的使用表明，本方案运行稳定、无故障，在响应时间、完整性验证等方面性能可靠且均能满足该信息系统要求。

6.5 存储代价和通信带宽

1) 存储开销

PPPDP方案的存储开销来自客户端和服务器端的存储开销，主要的开销是服务器端的存储开销，其他的开销很小可忽略不计。在预处理阶段利用椭圆曲线加密，能很好地减少密钥长度，但要生成用于不可否认的COM值，增加了一定的存储成本。但在性能上有很大的提高，存储的增加量可以通过增加数据块大小来减少额外的存储，在可以接受范围之内。PPPDP方案在客户端存储开销代价为(1)，文件的大小对开销没有影响，仅与安全系数存在相关性。

例如，存储文件大小为1 GB，对数据进行分块，数据块大小为4 KB，在S-PDP方案中，验证标签为1 024 bit，额外的存储开销为3.125%。PPPDP方案在验证标签部分增加了COM函数，存储的额外开销为数据块数与每个数据块验证信息所占存储的乘积，约为3.5%，由于每个数据块生成的验证信息大小固定，当分块变大时，额外的存储开销会逐渐下降，当数据块大小为64 KB时，存储的额外开销为2.75%。

2) 通信带宽

通信开销主要在验证者和服务器之间的挑战验证阶段产生。随着文件数据块的增大，验证信息总量逐渐减小，返回的证据信息也减小。S-PDP因为chal和证明都是恒定的，所需要的带宽为(1)，PPPDP方案所需带宽与S-PDP相同。在COM验证阶段，服务器需要一定的带宽来显示数据块和相关的COM，这仅与文件划分产生的数据块数量相关。

7 结束语

本文提出了一种基于公有验证和私有验证的数据持有性验证方法，在验证过程中可以同时验证客户端和服务器的可信性，查证验证是否满足不可否认性。在验证的过程中多次利用椭圆曲线，很好地保证了验证的安全性，并针对服务器和客户端的特点，为私有和公有验证设计了合理的挑战。2种验证方法使用同一套元数据，节省了计算和存储空间，验证效率优于原有的单纯私有验证或公有验证的方案。

由于云中数据是可以根据用户的需求随时进行修改的，下一步的工作主要涉及2个方面，一方面将在本文所提静态的验证方法的基础上，进一步研究适用于动态环境的数据持有性验证；另一方面，针对目前云中存储的数据具有多副本的特性，将对本文提到的多层次验证方案进行调整，研究适用于多副本的数据持有性验证方案。

[1] 王宏远, 祝烈煌, 李龙一佳. 云存储中支持数据去重的群组数据持有性证明[J]. 软件学报, 2016, 27(6):1417-1431. WANG H Y, ZHU L H, LI L Y J. Group provable data possession with deduplication in cloud storage[J].Journalof Software, 2016, 27(6): 1417-1431.

[2] 查雅行, 罗守山, 卞建超,等. 基于多分支认证树的多用户多副本数据持有性证明方案[J]. 通信学报, 2015, 36(11):80-91.ZHA Y X,LUO S S, BIAN J C, et al. Multiuser and multiple-replica provable data possession scheme based on multi-branch authentication tree[J]. Journal on Communications, 2015, 36(11): 80-91.

[3] 何凯, 黄传河, 王小毛,等. 云存储中数据完整性的聚合盲审计方法[J]. 通信学报, 2015, 36(10):119-132.HE K, HUANG C H, WANG X M, et al. Aggregated privacy-preserving auditing for cloud data integrity[J]. Journal on Communications,2015, 36(10): 119-132.

[4] 谭霜, 贾焰, 韩伟红. 云存储中的数据完整性证明研究及进展[J]. 计算机学报, 2015, 38(1): 164-177.TAN S, JIA Y , HAN W H. Research and development of provable data integrity in cloud storage [J]. Chinese Journal of Computers, 2015, 38(1):164-177.

[5] YUAN J, YU S. Efficient public integrity checking for cloud data sharing with multi-user modification[C]//IEEE International Conference on Computer Communications. 2014: 2121-2129.

[6] ATENIESE G, BURNS R, CURTMOLA R, et al. Remote data checking using provable data possession[J]. ACMTransactions on Information & System Security, 2011, 14(1):12.

[7] JUELS A, KALISKI B S, BOWERS K D, et al. Proof of retrievability for archived files, US 8381062 B1[P]. 2013.

[8] ARMKNECHT F, BOHLI J M, KARAME G O, et al. Outsourced proofs of retrievability[C]//SIGSAC Conference on Computer and Communications Security. 2014:831-843.

[9] ATENIESE G, BURNS R, CURTMOLA R, et al. Provable data possession at untrusted stores[C]//ACM Conference on Computer and Communications Security. 2007: 598-609.

[10] DAN B, LYNN B, SHACHAM H. Short signatures from the weil pairing[J]. Journal of Cryptology, 2004, 17(4): 297-319.

[11] WANG Q, WANG C, LI J, et al. Enabling public verifiability and data dynamics for storage security in cloud computing[C]// European Conference on Research in Computer Security. 2009:355-370.

[12] WANG C, CHOW S S M, WANG Q, et al. Privacy-preserving public auditing for secure cloud storage[J]. IEEE Transactions on Computers, 2013, 62(2):362-375.

[13] CURTMOLA R, KHAN O, BURNS R. Robust remote data checking[C]//ACM Workshop on Storage Security and Survivability. 2008: 63-68.

[14] WANG H, ZHU L, XU C, et al. A universal method for realizing non-repudiable provable data possession in cloud storage[J]. Security & Communication Networks, 2016, 9(14):2291-2301.

[15] HANSER C, SLAMANIG D. Efficient simultaneous privately and publicly verifiable robust provable data possession from elliptic curves[C]//International Conference on Security and Cryptography. 2015:15-26.

[16] 赵曼, 徐和根, 马峰. 基于椭圆曲线密码(ECC)算法的图像加密技术的硬件设计[C]//中国通信学会学术年会. 2012:18-21.ZHAO M, XU H G, MA F. Hardware design based on elliptic curve cryptography (ECC) algorithm for image encryption technology[C]// Annual Meeting of China Institute of Communications.2012: 18-21.

[17] PEDERSEN T P. Non-interactive and information-theoretic secure verifiable secret sharing[C]//International Cryptology Conference on Advances in Cryptology. 1991: 129-140.

[18] PEDERSEN T P. Non-interactive and information theoretic secure verifiable secret sharing[C]//International Cryptology Conference on Advances in Cryptology. 1991.

[19] DENT A W. The hardness of the DHK problem in the generic group model[J]. IACR Cryptology ePrint Archive, 2006: 156.

[20] MO Z, ZHOU Y, CHEN S, et al. Enabling non-repudiable data possession verification in cloud storage systems[C]//IEEE International Conference on Cloud Computing. 2014: 232-239.

[21] MCCURLEY K S. The discrete logarithm problem[C]//Symposium in Applied Math. 1990: 49-74.

Provable data possession scheme based on public verification and private verification

TIAN Junfeng1,2, CHAI Mengjia1,2, QI Liuling1,2

1. School of Cyber Security and Computer, Hebei University, Baoding 071002, China 2. Key Lab on High Trusted Information System in Hebei Province, Baoding 071002, China

More and more users choose to transfer their applications and data into the cloud. Data security is a key issue for cloud storage systems. To ensure the integrity and validity of the data stored in the cloud, provable data possession (PDP) scheme is particularly important. In order to verify whether the cloud storage service provider had stored the data of the user completely, a scheme on the basis of NRPDP (non-repudiable PDP) was improved and extended, and a data retention scheme based on public authentication and private authentication was proposed. The scheme can verify the trustworthiness of the service provider and the user in the cloud storage at the same time, which satisfies the non-repudiation of the verification. The theory proves the non-repudiation of the proposed scheme. The experiment proves that the efficiency of each stage is better than that of the existing single public verification method or private authentication method.

cloud storage, non-repudiation, provable data possession, public verification, private verification

TP309

A

10.11959/j.issn.1000−436x.2019053

2018−03−13；

2018−12−12

国家自然科学基金资助项目（No.61170254）；河北省自然科学基金资助项目（No.F2016201244）；河北省高等学校科学技术研究青年基金资助项目（No.QN2016149）

The National Natural Science Foundation of China (No.61170254), The Natural Science Foundation of Hebei Province (No.F2016201244), The Youth Fund for Scientific and Technological Research in Higher Institutions of Hebei Province (No.QN2016149)

田俊峰（1965− ），男，河北保定人，博士，河北大学教授、博士生导师，主要研究方向为信息安全与分布式计算。

柴梦佳（1993− ），女，河北保定人，河北大学硕士生，主要研究方向为信息安全与分布式计算。

齐鎏岭（1992− ），男，河北保定人，河北大学硕士生，主要研究方向为信息安全与分布式计算。