基于信息检测条件下的斜拉桥可靠度确定方法研究

2019-03-28宋福春段继鹏

北方交通 2019年3期

宋福春，段继鹏

(沈阳建筑大学交通工程学院沈阳市 110168)

1 研究背景

当下，由于斜拉桥具有简洁美观的外形、良好的跨越能力等优点，被国内外广泛运用到大跨度桥梁施工设计中。我国也从1975年首次在四川竣工的钢筋混凝土斜拉桥(76m)，发展成为完成当今世界最大跨度的斜拉桥—苏通大桥(1088m)的国家。虽然斜拉桥发展迅速，但是在进行实际结构的参数计算中，由于材料特性、几何尺寸、荷载分布等多种不确定因素的存在，其可靠度的计算与验证一直是急需解决的重点与难点。

2 理论基础

2.1 β约界法的改进

在一座斜拉桥体系中，把其划分为由n个单元共同组成的体系，通过有限元软件计算的方法，得到在各个外荷载的单独作用下，每个结构单元在应力与形变上的数据，并利用一次二阶矩法(JC)，计算第k阶段的失效历程，得出最小的可靠指标—β(k)min，在这一识别阶段，满足式(1)的单元rk为失效候选单元。

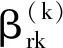
(1)

式中，c1=1.29和c2=0.86。

2.2 贝叶斯方法

通过对贝叶斯方法的运用，来对桥梁构件的可靠度进行研究。用E来表示斜拉桥结构某一构件信息检测这一附加事件，运用贝叶斯方法，可以得出失效事件F，在更新后的失效概率为：

(2)

2.3 构件可靠度的研究方法

对构件可靠度的主要研究方法为响应面法(RSM)，模拟真实极限状态曲面，是通过拟合一个响应面，能够简化可靠度计算过程，公式如下。

(3)

式(3)中，Xi为主要随机变量；a、bi、ci为待定系数；n为随机变量。通过Matlab语言，构造响应面函数，运用Matlab软件计算斜拉桥构件的可靠度。

2.4 斜拉桥可靠度的研究方法

根据改进的β约界法，建立出主要的失效模式和失效树模型，并构建计算结构体系可靠度的串并联系统。运用Matlab语言构造响应面函数，计算斜拉桥结构失效单元可靠度，并运用贝叶斯定理，对失效候选单元的失效概率及可靠指标进行修正，综合得到斜拉桥可靠度研究方法。

3 具体工程案例分析

3.1 分析模型

根据图1所示双塔双索面漂浮体系斜拉桥实例。桥跨组合为(146.3+335.3+146.3)m，主梁为钢箱梁，索塔为混凝土门型塔，斜索运用平行钢丝拉索。

基于ansys的apdl语言，建立了斜拉桥的参数平面有限元模型。假设作用在桥面上的车辆荷载采用均匀荷载形式。根据以往对斜拉桥进行分析的经验，车辆荷载仅在主跨上进行分别，对于斜拉桥的结构受力十分不利。因此，只考虑一种荷载布置方法：恒荷载+活荷载(主跨均匀分布)，平均荷载标准值q=10.5kN/m。斜拉桥的随机变量参数见表1。

图1 斜拉桥立面布置图(单位：m)

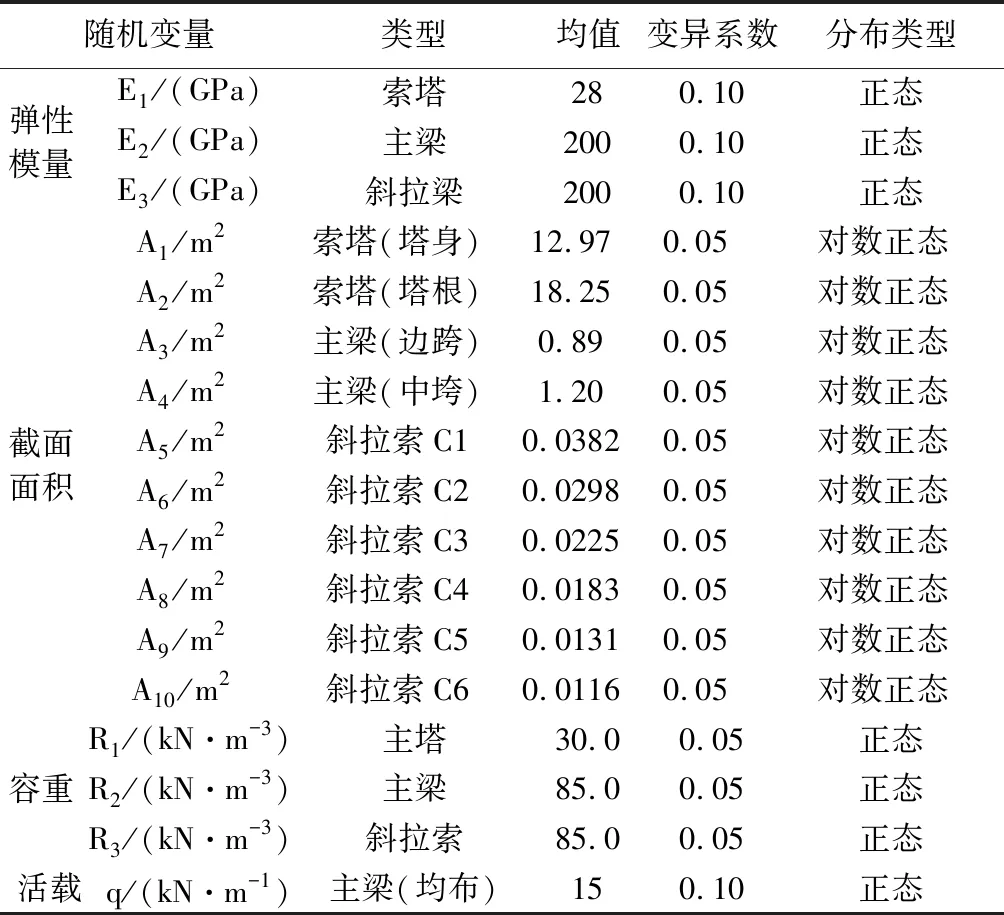
表1 斜拉桥相关统计参数

3.2 时变体系下的可靠度分析

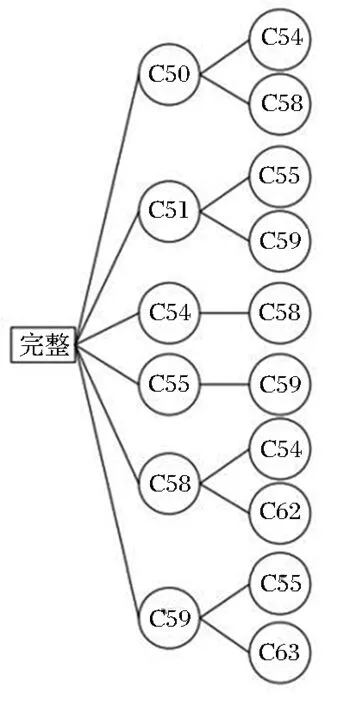
图2 失效树图

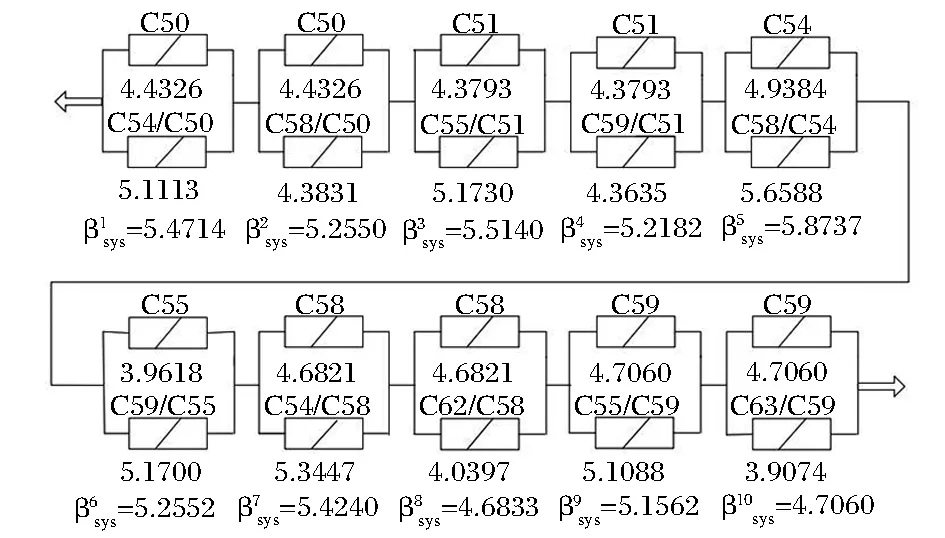
图3 斜拉桥的串并联系统

根据改进的β约界法，可以得到斜拉桥在建成初期时的前二级失效树，具体见图2，不难发现斜拉桥的失效单元都是索单元，说明索单元与主塔和主梁单元相比，可靠度明显较低。

文中假设15年末按最坏的情况计算，识别出的失效候选索单元均失效，假设斜拉索的有效截面积AC，根据服役时间呈现出线性变化，则有效截面积AC(t)计算公式如下：

(4)

式(4)中，t为年数，通过插值可以求出任意一年的AC(t)。考虑截面积退化的方式，对构件的退化进行模拟，则在t时刻，受力构件i的有效截面面积计算公式为：

Ai(t)=[1-DRi]×Ai(t-1)=[1-DRi]l×Ai(0)

(5)

式(5)中，Ai为构件i在t时刻的截面积，Ai(t-1)为构件i在t-1时刻的截面积，Ai(0)为构件i在初始状态的截面积，假设DRi=0.0025/年，计算索塔与主梁截面积随时间的变化而发生的规律，并按照上文所述方法进行体系时变可靠度的计算。为了使计算更加简便，假设各个结构的弹性模量、容重参数保持不变，按照式(4)和式(5)分别对斜拉索、主梁和主塔各个时段的截面面积值进行计算，得出的结果见表2。

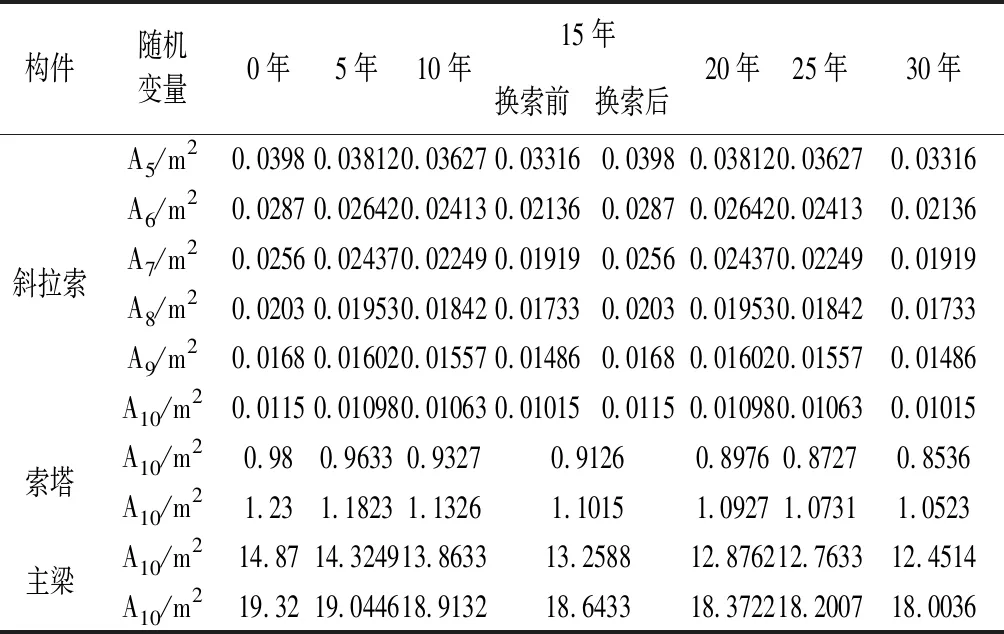
表2 斜拉桥随机变量(更新前)

桥梁承载能力在极限状态下，目标可靠度取3.50。由此可计算出在30年中吗，斜拉桥的体系可靠度β-T曲线，如图4所示。

3.3 斜拉桥检测信息的体系可靠度更新

根据失效树模型，建立了失效候选单元的检测方案，并每5年对失效候选单元进行一次检测。记录斜拉索的腐蚀情况和断线数。由于缺乏相关的资料与数据，根据表2，假设斜拉索断裂和腐蚀程度的信息检测由MATLAB数学软件组成，主梁和索塔的有效截面面积与表2一致。在使用的30年内，斜拉桥系统可靠度的斜拉索检测信息如表3所示。

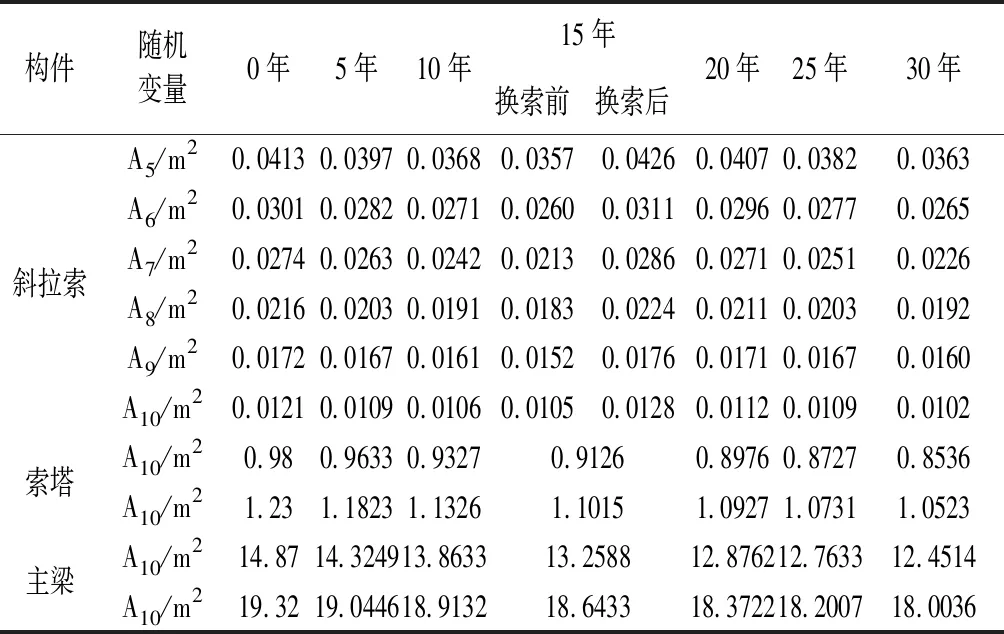
表3 斜拉桥随机变量(更新后)

假设失效候选单元在检测前后的失效模式之间的相关系数为0.95，则通过综合分析方法得到斜拉桥更新前后的系统可靠度β-t曲线如图4。

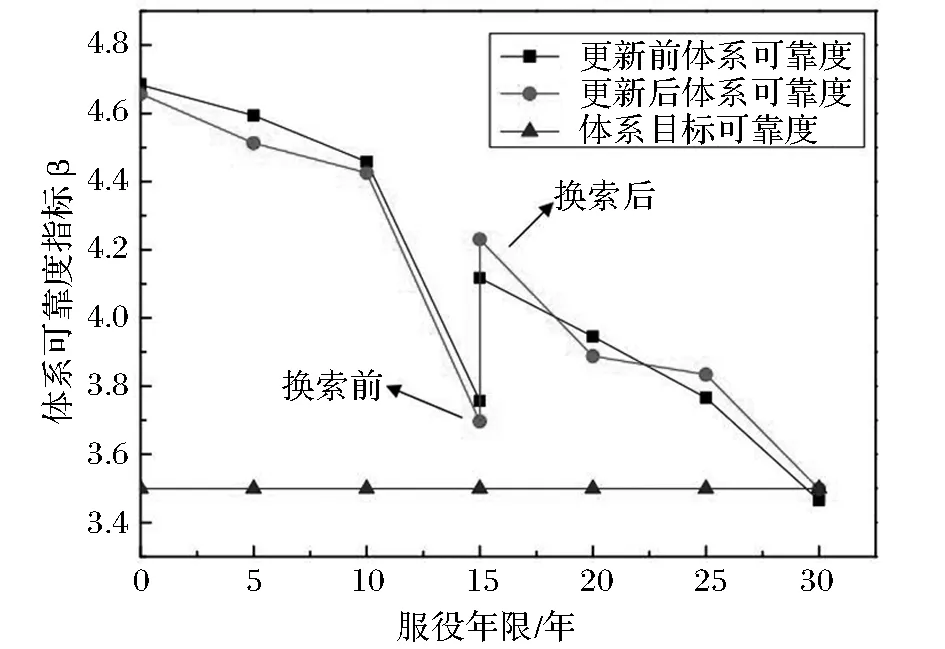
图4 可靠指标β与使用年限T的变化曲线

从图4可以看出斜拉桥系统在试验前后，其可靠度略有变化，但变化不大，并且该系统在30年服务期内的可靠指标均大于道路桥梁设计目标标准化标定的可靠指标3.50，显示结构系统处于可靠状态，系统的可靠指数略低于30年底目标的可靠指数。15年底变更后，更新前后系统的可靠指数增加到一定程度，但不会大于桥梁开始时系统的可靠指数。