基于模糊神经网络的涡扇发动机状态监控模型研究

卜旭东，魏智辉

（中国飞行试验研究院，陕西 西安 710089）

航空发动机为飞机提供飞行所需的动力，其健康状态直接关系到飞机能否安全飞行。在新机试飞过程中，尤其是单发飞机，发动机技术状态仍处于不断调整和完善的过程中，飞行风险较大。为了保证发动机安全可靠工作，对发动机状态参数进行实时监控十分重要。目前，发动机安全监控根据实时测量的参数是否超限来判断发动机是否正常工作，这种方式并不能检测出工作参数未超限但偏离正常值较大的情况，不能及时有效地检测到发动机异常状况。通过建立精确数学模型，将实时监控的参数与模型输出对比生成残差，对残差是否超过给定阈值及其变化趋势进行分析，可以有效地检测到异常状态。

建立发动机数学模型主要有部件法和系统辨识。Kong等采用Gasturbo软件实现发动机稳态和过渡状态的监控及预测[1]。部件法依赖完整、准确的部件特性，而且迭代算法复杂，难以满足实时性要求[2]。神经网络可以逼近任意非线性函数，无需深入了解发动机的内部结构和工作原理，具有算法简单、实时性好、易于实现等优点，在航空发动机模型辨识和参数预测中得到广泛的应用[3-9]。

发动机状态监控主要包括气路参数监控、滑油系统监控、振动监控、无损检测等4个方面[10]。而气路部件故障在发动机故障占比超过90%，维修费用占发动机总维修费用60%[11]，因而发动机趋势监控、故障诊断方面的研究大多基于气路参数的分析。传统的BP神经网络存在易陷入局部最优、隐含层网络结构的确定等问题，而T-S模糊神经网络对复杂非线性系统具有良好的辨识能力，相当于将输入空间划分为若干个模糊集合，在每个模糊集合建立局部线性化模型，然后基于隶属度函数将每个局部模型连接起来，形成全局模糊模型[12-13]。本文基于飞行试验数据采用T-S模糊神经网络对发动机气路参数进行辨识，建立辨识模型用于发动机状态监控。

1  基于减法聚类的 T-S 模糊神经网络

T-S 模糊神经网络在输入变量维数为m，每个维度划分为n个模糊集合时，那么就会产生nm个规则数。当输入数据维数较高、数据复杂时，T-S 模糊推理模型规则数变得庞大，难以迭代训练。基于此问题，Sugeno 和 Yasukawa 提出了一种根据模糊c均值聚类算法对样本进行模糊聚类，提取规则[14]。本文基于减法聚类算法划分样本数据，提取模糊规则，从而优化模糊神经网络的结构。

1.1  T-S 模糊推理系统

T-S模糊系统是一种自适应能力很强的模糊系统，该模型不仅能自动更新，而且能修正模糊子集的隶属函数。模糊推理系统共有4个模块：模糊化、模糊规则库、模糊推理机和去模糊化。

设辨识对象为P（X，Y），其中X为系统r维输入，Y为系统的q维输出，这样多输入多输出系统可以分为q个多输入单输出系统进行辨识。

（1）模糊化。将输入的精确值xj映射到模糊集合Ai，并求出隶属度μAij。

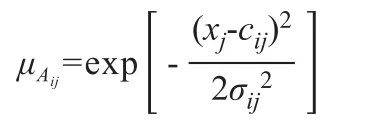
其中，xj为模糊模型第j个输入变量；Aij为变量xj第i个模糊子集；ci和σi为模糊集的中心和宽度。

（2）规则库。T-S模糊系统用如下的“if-then”规则形式来定义，第i条规则如下：

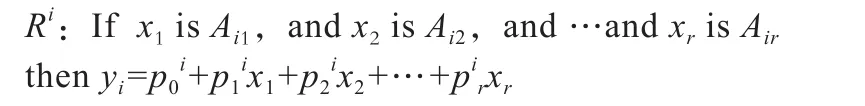
yi为第i条规则的输出；pir为模糊系统参数，该模糊推理表示输出为输入的线性组合。

（3）推理机。输出为所有输入隶属度的乘积，表示该条规则在输出中的权重大小。

ωi=μAi1*μAi2*…μAir

（4）反模糊化。将推理得到的模糊输出值转化为精确值y。

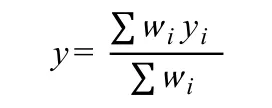
1.2 减法聚类算法原理

减法聚类是用来自动估计数据中的聚类个数及其聚类中心的算法。设训练时采用的样本为M维空间的n个数据点，数据归一化后点xi的密度指标Di可以定义为：

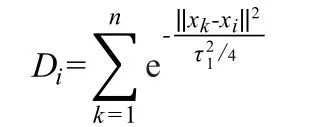
所谓密度指标，即xi与其他数据欧氏距离之和。如果xi周围数据点密集，那么密度指标越大。式中τ1定义了xi的一个邻域，τ1以外的数据对密度指标影响较小。计算每个数据点的密度，选取密度指标最大的数据点作为第一个聚类中心xc1，对应的密度指标为Dc1，再根据下式重新计算各数据点的密度指标：

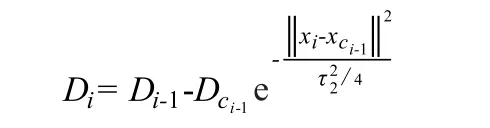
1.3  T-S 模糊神经网络

T-S模糊推理系统在各参数如隶属度函数中心c和宽度d、规则层中的系统参数p的调整和训练方面存在缺陷，利用神经网络的自适应学习算法来进行训练，能够较快地收敛，获得一个效果较好的T-S模糊推理系统。T-S模糊神经网络的学习算法为误差反向传播 BP算法。

（1）误差计算：

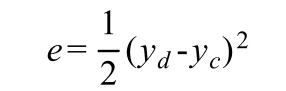
式中，yd是网络期望输出；yc是网络实际输出；e为期望输出与实际输出的误差。

（2）系统参数修正

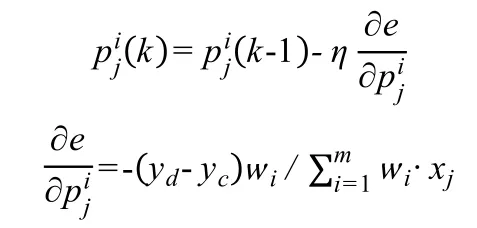
式中，为神经网络系数，η为学习率，xj为网络输入参数，wi为输入参数隶属度连乘积。

（3）隶属度参数修正

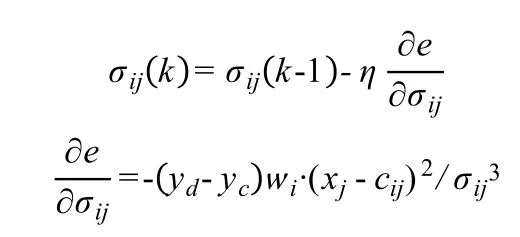
cij、σij为隶属度函数的中心和宽度。

2  涡扇发动机气路参数模型辨识

2.1  神经网络模型输入、输出参数

本文针对发动机的气路参数进行辨识，将训练好的神经网络应用于发动机状态监控，帮助检测发动机异常状况。神经网络输入为决定发动机工作状态的参数：飞行马赫数Ma、气压高度Hp、大气总温Ttb、发动机油门杆角度Φ。模型的输出参数为发动机的气路参数，包括：高压转子转速NH、低压转子转速NL、高压压气机出口总压P31、低压涡轮出口总温T6、低压涡轮出口总压P6、低压压气机进口导叶角角度α1、高压压气机导叶角角度α2、喷管喉部面积A8等。而目前航空发动机控制参数α1、α2、A8是根据NH、NL控制调节的，因此本文不针对这3个气路参数进行辨识。为了使神经网络能够拟合发动机推拉油门杆各参数动态变化过程，在输入层中加入前一时刻的油门杆角度、输出变量前两个时刻的反馈，差分方程描述如下：

NH(k+1)=f1(Ma(k),Hp(k),Ttb(k),Φ(k),Φ(k-1),NH(k),NH(k-1))

NL(k+1)=f2(Ma(k),Hp(k),Ttb(k),Φ(k),Φ(k-1),NH(k),NL(k),NL(k-1))

T6(k+1)=f3(Ma(k),Hp(k),Ttb(k),Φ(k),Φ(k-1),NH(k),T6(k),T6(k-1))

P31(k+1)=f4(Ma(k),Hp(k),Ttb(k),Φ(k),Φ(k-1),NH(k),P31(k),P31(k-1))

P6(k+1)=f5(Ma(k),Hp(k),Ttb(k),Φ(k),Φ(k-1),NH(k),P6(k),P6(k-1))

2.2  试飞数据中训练样本的选取

未经处理的试飞数据包含大量发动机工作状态相近、重复的数据点，这些数据不具有代表性，占用大量的计算资源。本文以数据点Pi中飞行马赫数Ma，气压高度Hp，发动机油门杆角度Φ，高压转子转速NH，低压涡轮出口总温T6等反映飞行条件、发动机工作状态的5个参数之间的Euclidean距离作为评价发动机工作状态相似程度的指标，即：

基于K-means聚类算法对某型号发动机试飞期间15个架次的试飞数据进行聚类，选取各类别中距离聚类中心最近的数据点组成训练样本，筛选出1000个训练样本，在飞行包线内的分布如图1所示：

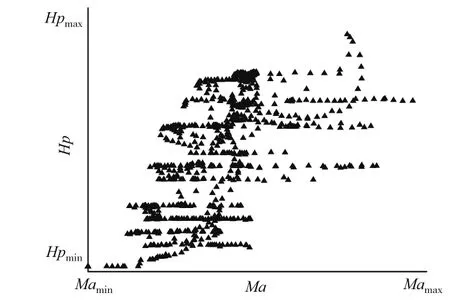
图1 飞行试验数据样本在飞行包线内的分布

2.3  神经网络训练学习

神经网络训练前对输入输出数据进行归一化处理，减法聚类后确定NL、NH、T6、P31、P6的模糊规则数分别为17、20、31、16、15。采用均方差MSE函数以及相对误差δ评价网络模型的性能。

3  结果分析与讨论

3.1  网络模型辨识结果

在神经网络实际应用中，人们所关心的并不是网络对已知输入输出样本的拟合能力，而是训练后的神经网络能否对非训练样本具有较好的预测精度。为了验证网络模型的泛化能力，取未参与训练、发动机正常工作的试飞数据进行仿真对比。以该型号发动机在高度为8km，马赫数为0.75飞行条件下加减速试飞数据对网络模型的泛化能力进行验证，飞行过程中油门杆角度变化情况如图2所示，将模型的输出与试飞数据进行对比，对比结果如图3所示。

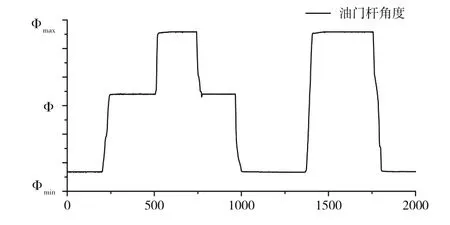
图2 验证样本中油门杆角度变化曲线

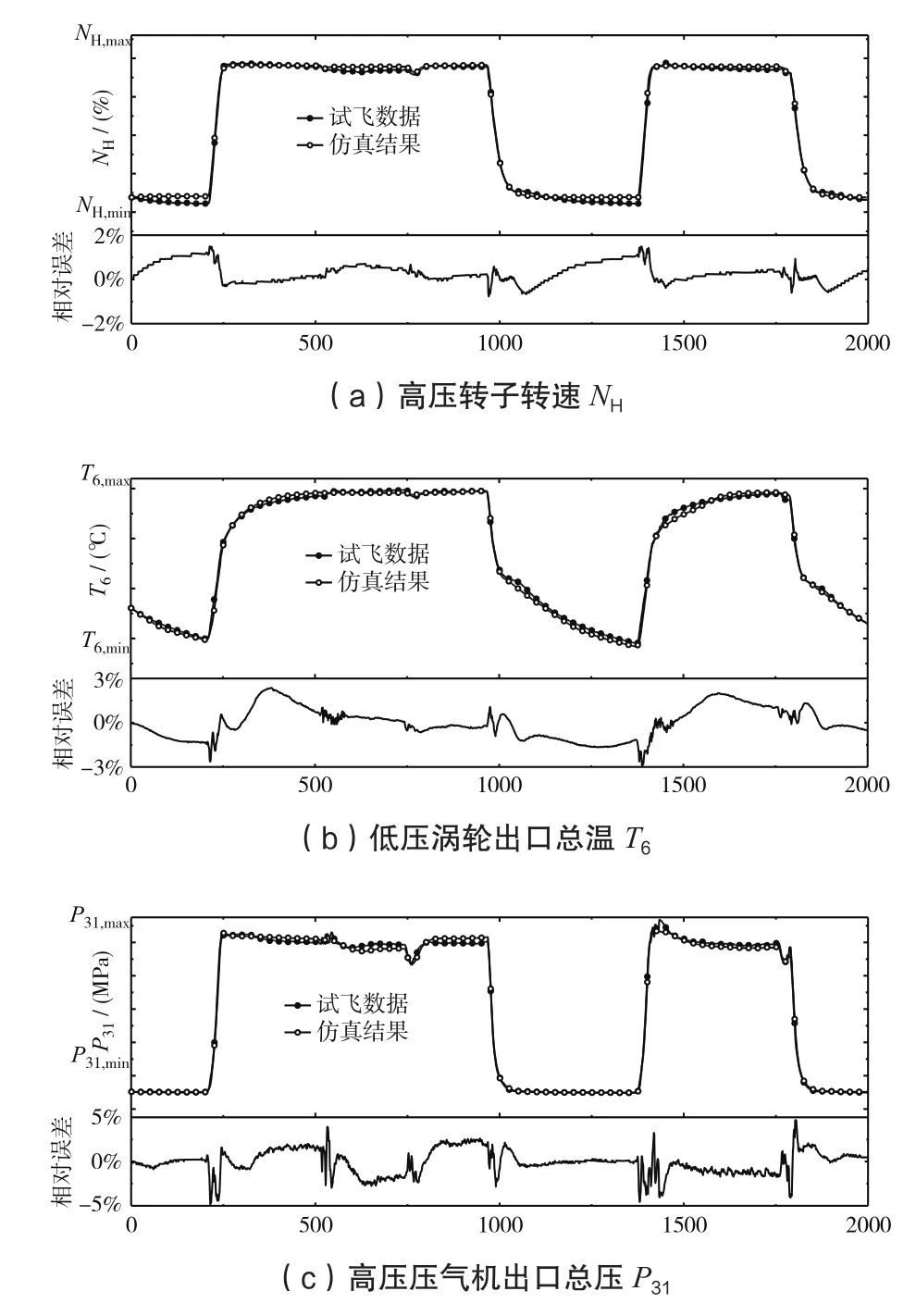
图3 涡扇发动机辨识模型输出与试飞数据对比

表1 模型辨识结果均方差和最大相对误差

图3 给出了气路参数模型NH、T6、P31的推广验证结果，空心圆点划线为辨识模型输出结果，实心圆点划线为试飞数据，下半部分图表黑色实线为两者相对误差。该段加减速试飞中，辨识模型的输出结果与试飞数据吻合较好，稳态阶段误差较小，推拉杆气路参数瞬态变化过程误差相对较大，模型最大相对误差分别为：低压转子转速δmax=1.87%，高压转子转速δmax=1.50%，低压涡轮出口总温δmax=2.94%，高压压气机出口压力δmax=4.36%，低压涡轮出口总压δmax=4.86%，如表1所示。

3.2  故障检测

根据机载测试系统实时测量的飞行参数、油门杆角度计算发动机气路参数，与测量结果对比得到相对误差，以相对误差大小作为故障检测的依据。依据模型在验证样本上计算结果，给定NL、NH、T6、P31、P6的相对误差阈值分别为2%、2%、3%、5%、5%，根据相对误差是否超过阈值判定发动机是否异常。以该型号发动机试飞中，高度为11km，马赫数为1.2飞行条件下一段发生喘振故障的试飞数据进行验证，辨识结果如图4所示：

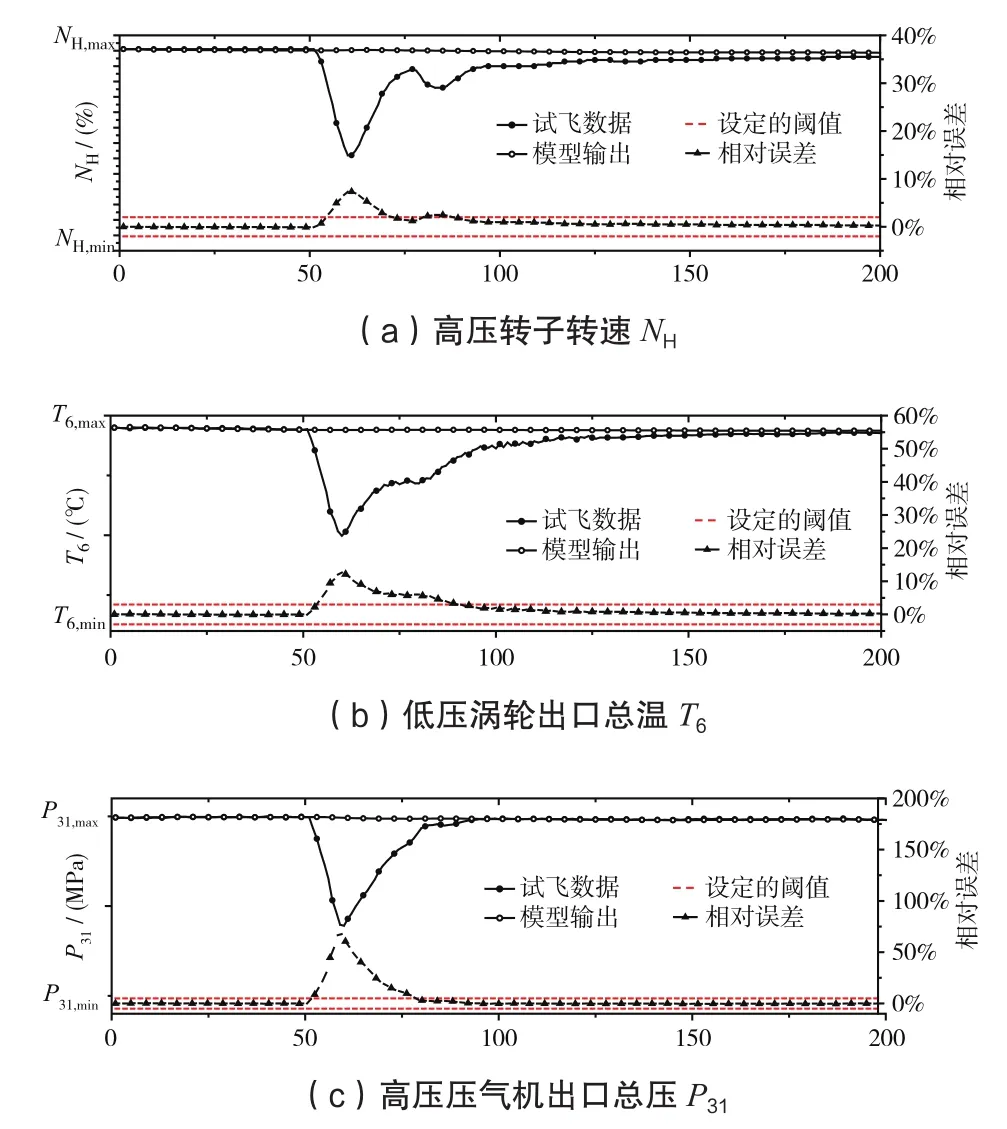
图4 辨识模型故障检测结果

图4 可以看出，从第50个数据点开始气路参数逐渐发生异常，模型的输出值与试飞结果相对误差迅速增大超过设定的阈值而报警，在发动机消喘系统的作用下，气路参数逐渐恢复正常，相对误差回到给定阈值之内。在喘振故障数据飞行试验上验证表明，该模型能够及时有效地检测出发动机气路参数异常。

4  结论

通过对某型涡扇发动机试飞数据进行聚类分析，划分输入空间以及确定规则数，基于T-S模糊神经网络建立辨识模型，在非训练样本上进行验证，结果表明网络模型计算结果与试飞数据基本吻合，推拉油门杆发动机气路参数瞬态变化过程拟合精度相对较差，高、低压转子转速相对误差不超过2%，涡轮后排气温度相对误差不超过3%，高压压气机、低压涡轮出口总压误差不超过5%。

在一段发生喘振的故障数据中推广应用，辨识模型能及时检测出发动机气路参数异常状况，该模型可用于该型号发动机后续试飞中状态监控。