一种改进的基因功能网络术语相似度计算方法*

唐 智 刘志明 罗凌云 欧阳纯萍 万亚平

(南华大学计算机学院 衡阳 421001)

1 引言

基因本体(Gene Ontology，GO)是生物医学领域最成功的本体之一，为描述基因(基因产物)的分子功能、生物过程等相关信息提供一个规范、准确的术语集,目前被广泛应用于生物医学相关研究领域[1]。主要体现在基因功能比较与分析、蛋白质相互作用预测、基因集合富集分析等诸多领域，由此成为不可或缺的生物医学本体。基因本体最初由基因本体组织(Gene Ontology Consortium)于1998年建立[2]。随着基因本体的发展，越来越多的模式生物数据库加入基因本体组织中，包括大多数主要的植物、动物和微生物数据库，截至目前基因本体已经能够为100多个物种提供注释信息[3]。

在生物学中，从特定的功能信息出发，查找与其功能相似或者相关的蛋白质，对这些蛋白质间关联程度进行比较量化是生物信息学研究中经常遇到的问题[4]。然而功能相似或者相关的蛋白质并不一定具有较强的序列上的相似性，基因本体的出现为解决这一问题提供新的途径。研究表明如果两个基因产物的功能相似，那么它们在GO中注释的术语就越相近[5]。所以GO应用的一个重要方面就是对术语语义的相似性进行度量，从而计算基因产物的相似度[6]。为更好地计算术语的相似度，本文提出一种基于融合高斯核函数的重启随机游走的基因本体术语相似度算法RWRSM。

2 现有基因术语间语义相似度计算方法

2.1 基于基因本体的方法

近年来高通量生物学技术的显著改进导致生物学数据的指数增加。基因本体是用于解释生物实验结果的最流行的生物信息学资源之一。GO提供结构化、受控制的术语词汇表，通过分子功能、生物过程和细胞成分3种属性来描述基因[7]。在每个类别中术语被构造为有向无环图(Directed Acyclic Graph，DAG)。基于GO的语义相似性已成功应用于许多研究领域，如基因功能预测[8]、基因网络分析[9-10]、同源性分析[11]、基因关联可视化[12]和缺失价值估算[13-14]。基于基因本体来计算基因功能相似性的方法[15-20]可分为4种类型：基于路径长度的方法、基于节点信息的方法、综合方法和基于基因功能网络的方法。基于路径长度的方法通过考虑GO拓扑结构信息[21]来计算相似度。最近提出的方法称为相对特异性相似性(Relative Specificity Similarity，RSS)，考虑两种类型的长度信息：从给定术语对到其最接近的叶子术语的边长和到最低共同祖先(Lowest Common Ancestor，LCA)节点的边长关系。但是基于边缘的方法完全依赖于基因本体的拓扑结构。这种方法不能在相同的拓扑水平上区分术语。对于基于节点的方法，这些方法依赖于特定的分类法。该方法利用信息量最大的共同祖先(Most Informative Common Ancestor，MICA)的信息内容(Information Content，IC)来测量两个GO术语之间的相似性[22]。评估测试显示结果与蛋白质序列相似性一致，但是基于节点的方法仅考虑注释，忽略GO的拓扑信息。在综合组中，提出在GO中使用更多信息的方法。混合相对特异性相似度(Hybrid Relative Specificity Similarity，HRSS)使用4种类型的信息(信息内容、结构拓扑、注释和MICA)来计算语义相似性[21]。InteGO方法提出一种基于秩的方法来整合多种现有相似性方法，称为种子方法，以考虑GO的更多方面[16]。InteGO2方法通过投票方法从一组方法中选择最合适的方法，并基于元启发式搜索方法[12]整合这些选定的方法。评估测试表明综合方法比种子方法表现更好。但是所有这些方法都只基于GO结构信息，忽略GO的不准确表示和缺失的信息等问题。如只有37%的拟南芥基因具有GO的所有3个结构域的实验注释[23]。因此GO中的不完整信息可能导致低质量的相似性。

2.2 基于网络的方法

最近提出一种基于网络的计算方法(Network-based Similarity Measure，NETSIM)，通过整合基因关联和GO拓扑结构和注释来解决这些问题[18]。基于代谢反应图的实验表明通过结合基因关联可以增强语义相似性，但NETSIM只考虑网络中的直接链路，使计算过程中只使用基因协同功能网络中的部分信息，实际上除直接连接的基因对外还应考虑基因功能网络中包含的间接基因相互作用。因此一种新的基于网络的NETSIM2被提出，通过随机游走的方法考虑基因协同网络中的直接和间接相互作用，代谢反应图的实验表明结果远高于之前所有算法，但是NETSIM2方法测量出的LFC值不够稳定，大部分LFC值很小。为解决这个问题本文通过使用高斯核函数来计算边权重，生成归一化加权矩阵PT，通过随机游走算法得到每对基因之间的相关性得分。最后基于NETSIM2原有算法计算术语对相似度。与之前方法相比本文算法融合高斯核函数与随机游走计算基因相关性得分，以考虑直接和间接的交互，通过有效地整合基因功能网络大大提高LFC值的稳定性。

3 改进的基因术语间语义相似度计算方法

3.1 融合高斯核函数与随机游走计算基因相关性得分

3.1.1 生成随机游走图 重启随机游走图构建基本思路是: 将训练集合D中的每个训练数据d∈D映射为图中的一个点, 根据两点之间的相关程度决定是否用边将两点相连。为方便求解, 一般构建成完全图, 将两点之间的相似度作为边的权重。当两点之间的相似度很小或者为0时, 节点之间边的权重做零值处理。假设加权图用G=(V,E)表示,V是图G中的节点集合,E是图G中边的集合, 其中节点个数为n。边权重使用高斯核函数计算, 公式如下:

(1)

其中σ是个参数变量，经验设定σ=∑i≠i||xi-yi||/[n(n-1)]。dij为两个图像节点之间的欧式距离，表示为：

(2)

3.1.2 随机游走过程 在使用重启随机游走算法之前先根据权重矩阵计算图G的概率转移矩阵P:

(3)

通过以下步骤计算基因之间的相关性得分。首先根据计算出的概率转移矩阵P，然后生成归一化加权矩阵PT。最后基于RWR的方法可以描述如下:

Di(t+1)=a·PTDi(t)+(1-a)ei

(4)

其中ei是表示初始状态。公式(4)的稳态解为：

Di=(1-a)(1-aPT)-1ei

(5)

其中Di是|V|×1向量，ei是|V|×1起始向量。(1-a)被定义为重启概率，其值在0和1之间。之后可以得到矩阵S，保存N(V，E)中每对基因之间的相关性得分。

3.2 计算两个GO术语之间的相似性

根据Peng等在以往的工作[24]中所表示的方法，计算两个术语之间的相似性，这两个基因本体术语对结合来自基因功能网络和GO的信息。设t1和t2为两个术语。将D(t1，t2)定义为基因集距离，以计算由t1和t2注释的基因组之间的相似性。D(t1，t2)定义为：

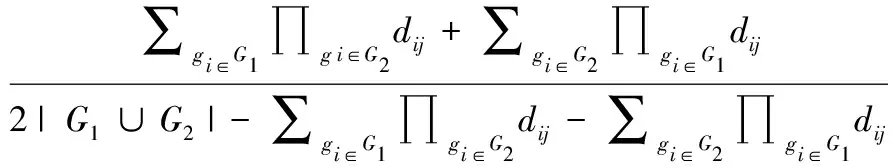
(6)

其中G1和G2分别是由t1和t2注释的基因集合。dij是两个基因之间的距离得分,dij=1-Sij。Sij是基于RWR的方法计算基因i和j之间的相关性得分。所有术语对的基因集距离在0～1之间归一化。然后基于标记为U的路径约束注释来计算两个术语之间的相似性。在传统的基于LCA的方法中，考虑LCA的所有后代。路径约束注释方法仅使用与比较术语最相关的术语。相关术语集包括3个部分：由术语t1和t2注释的基因集、由共同父节点注释的基因集p及其后代项在t1或t2到p的路径上。设t1和t2为两个GO的两个术语对，p为它们的共同祖先。t1和t2之间的相似性根据Peng等在以往工作[24]中提出的方程定义。

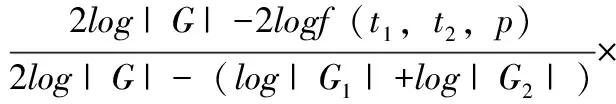
(7)

其中Gp(或G)是由共同祖先术语p(或根词)及其后代注释的基因集。在等式中f(t1,t2,p)基于路径约束注释计算相似性，定义如下:

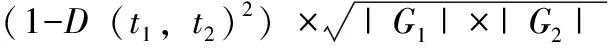
(8)

h(t1,t2)是测量共同父母的特异性，定义如下：

h(t1，t2)=D(t1，t2)2×|G|+(1-D(ti，t2)2)×
max(|G1|，|G2|)

(9)

在公式(9)中，左侧部分测量从项t1和t2到p的距离，右侧部分计算从p到根的距离。如果存在多于一个最低共同祖先则选择最高得分作为t1和t2之间的相似性。

4 术语相似度算法性能测试与分析

4.1 基于基因相似度的模型测试方法

虽然有很多方法可以评价基因功能相似度，但是没有直接的方法来衡量两个基因本体术语的相似度。因此首先基于术语相似度计算得到基因相似度，然后借助基因之间关系来衡量术语相似度计算模型性能。这一方法在相关研究中被广泛使用。为保证公平性，对于所有被比较的模型，通过使用相同的基因本体术语相似度来计算基因相似度并用此结果衡量术语相似度计算模型性能。如果计算某一物种对应的所有基因本体术语之间的相似度，就可以计算该物种中任意两个至少被一个基因本体术语注释的基因之间的相似度。给定两个基因gi和gj以及注释它们的术语集合Ti和Tj，为计算基因相似度，利用Wang等提出的方法将多对术语相似度累积成基因相似度，如公式(10)所示：

(10)

公式中对于属于集合Ti的每个术语，sim(t,Ti)表示术语t和术语集合Ti中术语之间相似度的最大值，如公式(11)所示:

sim(t,Tj)=,maxtj∈TjS(t,Tj)

(11)

公式中S(t,t1)表示t和tj的所有最小公共祖先中S(t,ti,p)的最大值。

基于EC编号(酶学委员会)组信息进行评估，由相同EC编号标记的基因具有相似功能。基因根据其EC编号(完整的4位数)分组到不同类别。然后测试同一类别的基因是否具有更高的相似性。在数学上使用记录的倍数变化(Logged Fold Change，LFC)度量[24]进行定量评估。对EC编号的ei类别LFC分数计算如下:

(12)

其中G(ei)是基因组，是ei由标记类别的基因组成;其中满足G(ei)∩G(ei)=Ø，diffa(ei,ej)定义如下：

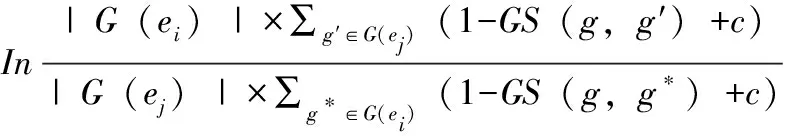
(13)

其中G(ei)是不包括g的ei基因集;c是拉普拉斯平滑参数;GS(g,g′)、GS(g,g*)由公式(10)定义。等式(13)测量EC间距离和EC内部距离之间的差异。基于公式 (12)中对对数差异倍数(LFC)得分的定义，如果一个模型的对数差异倍数得分越高，那么该模型的性能越好。

4.2 实验数据与结果

4.2.1 实验数据 2018年6月从GO网站下载GO结构和注释(www.geneontology.org/)工作中只使用“is-a”、“part-of”两种术语之间的语义关系。考虑到数据量太大、时间复杂度过高，所以使用基因数目相对较少的YeastNet中包含的基因关联对酵母菌进行评估测试。酵母菌的EC分组可以从www.yeastgenome.org/下载。

4.2.2 实验结果 通过比较不同EC类别和相同类别的基因之间的关系，根据GO的相似性来评估本文提出的改进算法性能。使用YeastNet中包含的基因关联对酵母进行评估测试。LFC评分作为标准与目前该领域LFC评分最高的两种算法NETSIM和NETSIM2进行比较。NETSIM、NETSIM2与本文中改进的算法RWRSM测量比较每个EC组的LFC得分，结果显示本文算法在所有104组EC编码中有88组具有最高LFC得分，占所有分组的84.6%，而其他算法只有15个EC中具有最高LFC得分，基于NETSIM、NETSIM2及算法RWRSM对酵母菌数据表现最佳LFC评分的EC数量，见图1。RWRSM算法的LFC评分针对与酵母菌的EC分组结果显示在所有评估测量中RWRSM的平均值最高，见图2。3种计算方法计算出的LFC平均值分别是RWRSM 0.575、NETSIM 20.547、NETSIM 0.534。3种算法的折线统计，见图3。其中RWRSM算法的折线趋于稳定在0.6左右，并且在所有EC类别中最高LFC分值占比达到85%以上，明显优于其他算法。

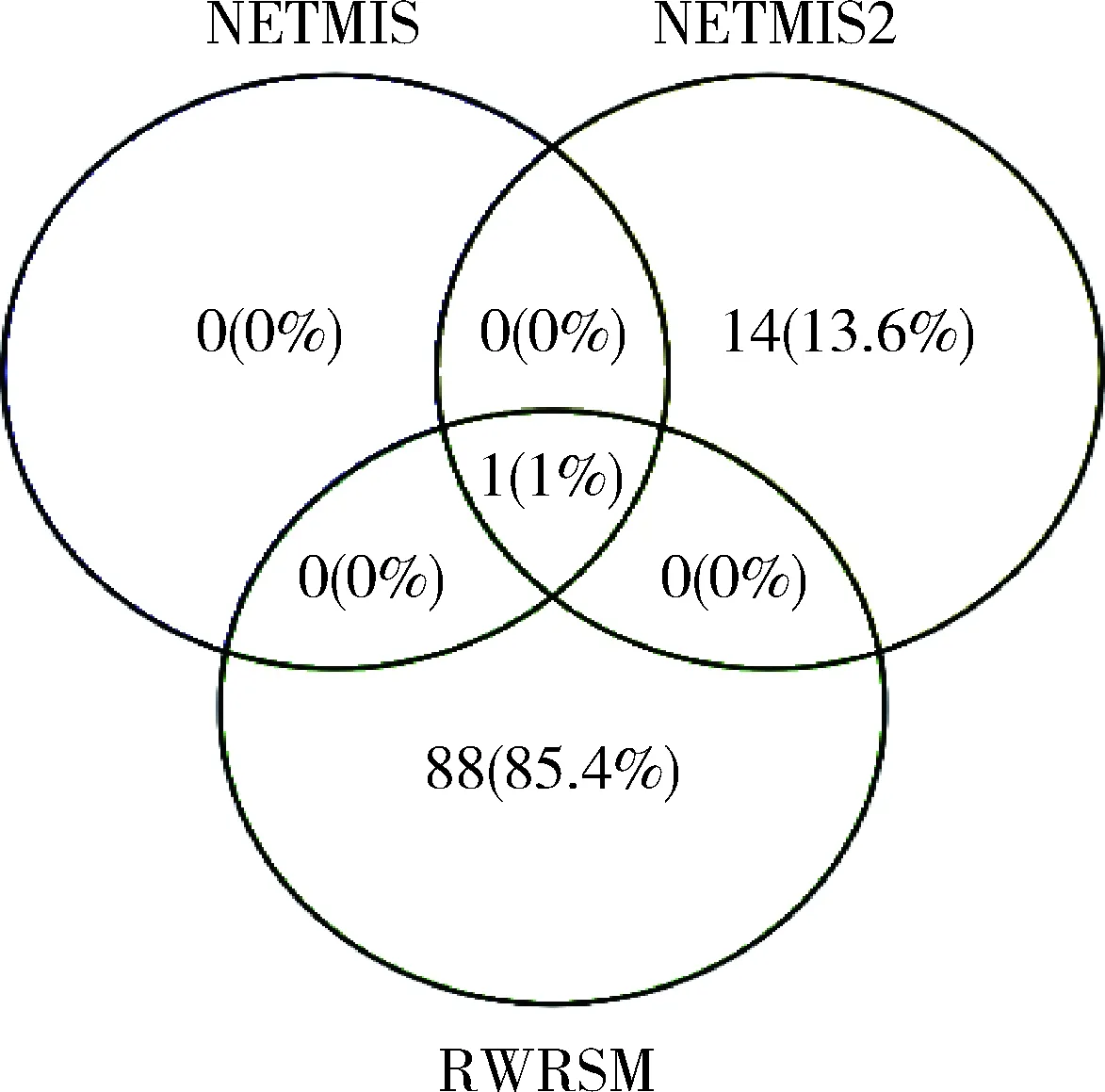
图1 基于NETSIM、NETSIM2及RWRSM算法在酵母菌中表现最佳LFC评分的EC数量

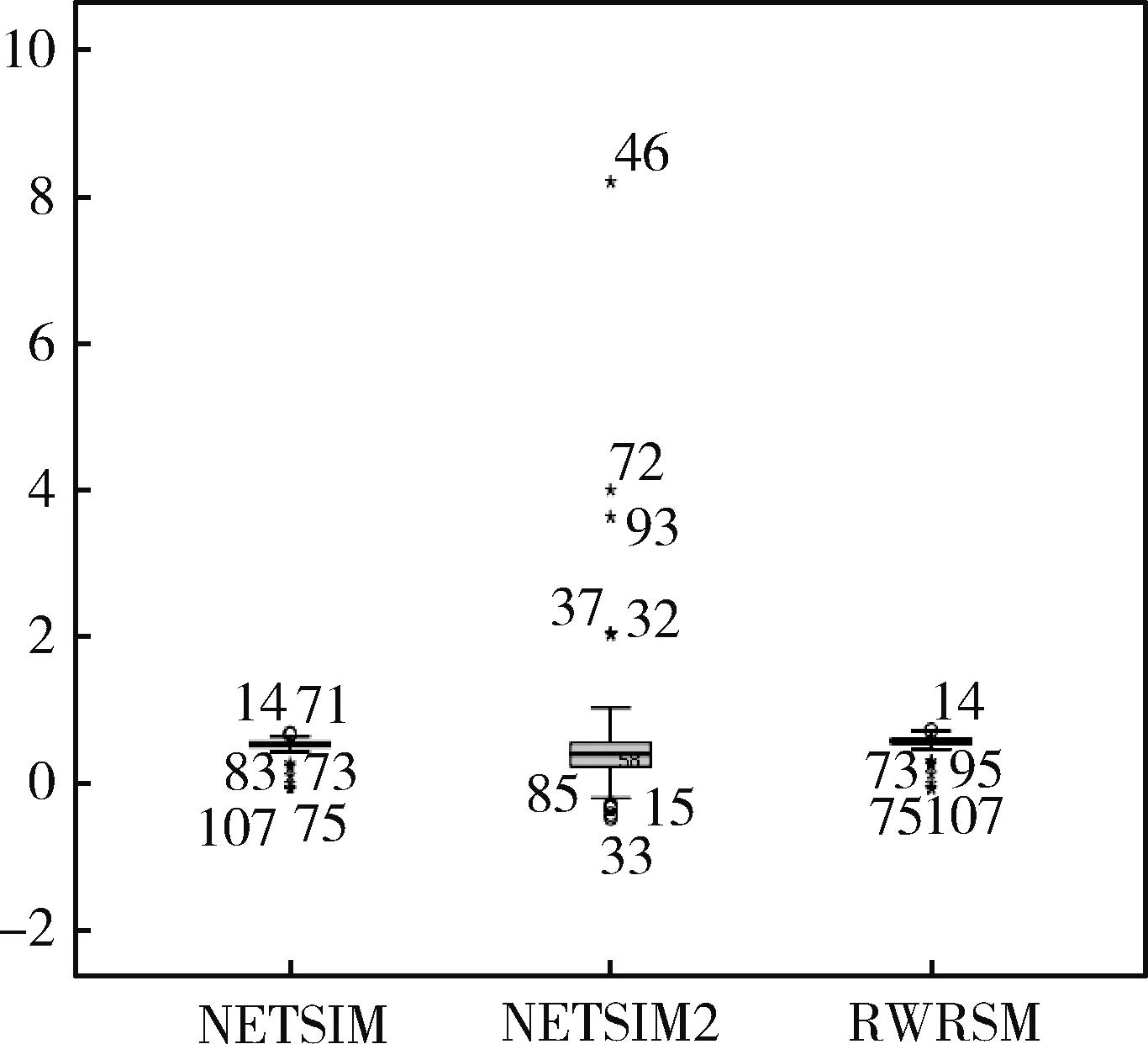
图2 GO酵母LFC相似性测量得分性能比较

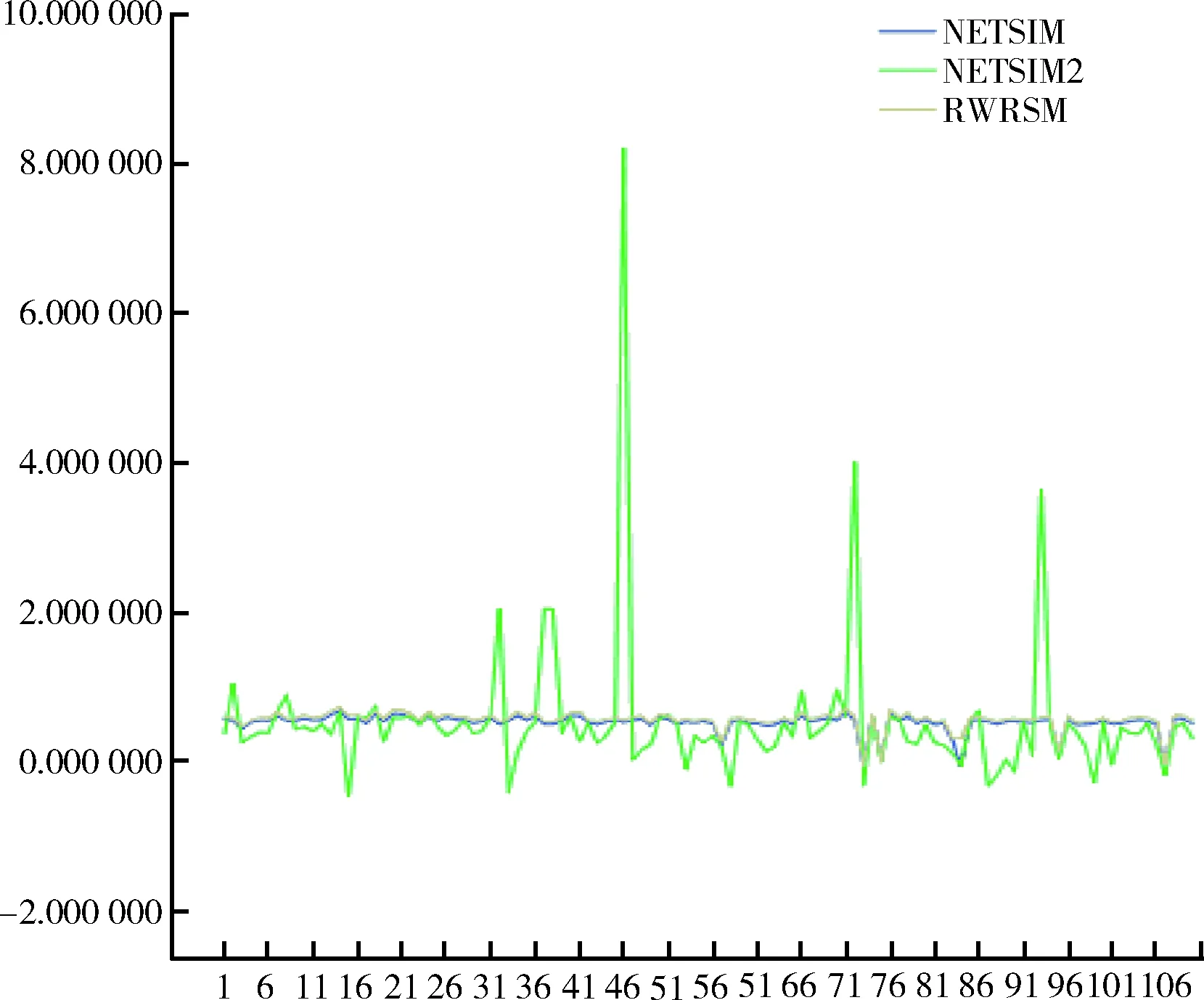
图3 3种算法LFC相似性得分性能折线

5 结语

基因本体论是用于描述基因和基因产物特性的最流行的生物信息学资源之一。计算基于GO的基因功能相似性已被广泛用于多个研究领域。然而低质量的相似性可能源于GO的不完整信息和有限的注释量。NETSIM通过考虑基因关联、GO结构和注释来解决这些问题。但其仅使用基因共功能网络中的本地关联信息，因为NETSIM仅考虑网络中的直接链路。后来提出的NETSIM2虽然考率到网络结构的全局性，但是实验结果表明LFC评分不够稳定。本文提出一种新的基于NETSIM2网络的改进算法，对基于RWR的方法考虑共功能网络全局结构，融合高斯核函数得到权重矩阵，包括3个步骤：首先，给定基因共功能网络融合高斯核函数得到权重矩阵，基于随机游走和重启方法计算两个基因之间的相关性得分矩阵;其次，通过组合来自共功能网络和GO的信息计算两个GO项之间的相似性;最后，选择GO术语对使用基于标准分数的方法测量两个基因的相似性。EC实验结果表明本文算法在酵母数据集的所有测量中表现最佳，LFC结果更加稳定。在所有104个EC中有88个具有最高LFC得分，占所有分组的84.6%，而其他算法只有15个EC中具有最高LFC得分，平均值也明显高于其他算法，测量出的LFC评分结果更加稳定。