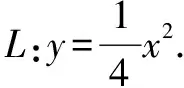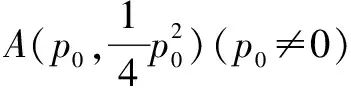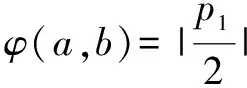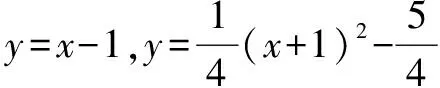自定义信息解答题的功能及特点

朱恒元

(浙江省义乌中学 322000)

高考数学命题有一条重要原则，那就是“既考查中学数学的知识和方法，又考查考生进入高校继续学习的潜能”.学习潜能如何考查？通常采用“自选动作”，通过自定义信息题考查学生即时学习的能力.自定义信息题可以有效考查学生收集信息、提炼加工、灵活运用的学习潜能.自定义信息题，过去在选择、填空题中频频出现，而今在解答题中也量增质高.下面略举数例，着重谈谈它作为“压轴性”解答题的功能及特点.

一、自定义集合

例1 记所有非零向量构成的集合为V，对于a，b∈V，a≠b，定义V(a，b)={x∈V|x·a=x·b}.

(1)请你任意写出两个平面向量a，b，并写出集合V(a，b)中的三个元素；

(2)请根据你在(1)中写出的三个元素，猜想集合V(a，b)中元素的关系，并试着给出证明；

(3)若V(a，b)=V(a，c)，其中b≠c，求证：一定存在实数λ1，λ2，且λ1+λ2=1，使得a=λ1b+λ2c．

解析(1)比如a(1，2)，b=(3，4)，设x=(x，y)，由x·a=x·b，可得x+2y=3x+4y，即为x+y=0，则集合V(a，b)中的三个元素为(1，-1)，(2，-2)，(3，-3).

(2)由(1)可得这些向量共线．

(3)证明：设x=(s，t)，a=(a，b)，b=(c，d)，y=(u，v)，c=(e，f).

若V(a，b)=V(a，c)，

即有as+bt=cs+dt，au+bv=ue+fv，

点评本题以平面向量为载体自定义一个集合，考查平面向量的数量积、共线向量等基础知识，考查向量运算的基本技能以及观察、归纳、推理能力．

二、自定义函数

例2 已知函数f(x)，定义

(1)写出函数F(2x-1)的解析式；

(2)若F(|x-a|)+F(2x-1)=0，求实数a的值；

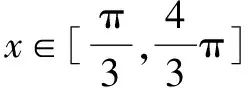
当2x-1>x，可得x>1，则F(2x-1)=1；

当2x-1=x，可得x=1，则F(2x-1)=0；

当2x-1

(2)当x>1时，F(2x-1)=1，F(|x-a|)=-1，

即有|x-a|1恒成立，

即有a2≤2a，解得0≤a≤2.

当x=1时，F(2x-1)=0，F(|x-a|)=0，

可得|1-a|=1，解得a=0或2；

当x<1时，F(2x-1)=-1，F(|x-a|)=1，

即有|x-a|>x恒成立，即为a2≥2ax在x<1恒成立，

即有a2≥2a，解得a≥2或a≤0.

综上，a的值为0或2.

可得cosx=0或F(x+sinx)=0，

则h(x)的零点个数为2；

当x+sinx=x，即x=π时，h(x)=0；

综上可得，h(x)的值域为(-1，1)．

点评本题通过自定义“复合”函数，考查函数的解析式、定义域、值域、零点和三角函数求值等基础知识，考查分类讨论的思想方法以及分析问题的综合能力．

三、自定义数列

例3 对任意正数M，取正整数对于项数为m的有穷数列数集{an}，记bk=max{a1,a2,…,ak}(k=1,2,…,m)，即bk为a1,a2,…,ak中的最大值，并称数列{bn}是{an}的控制数列.如1,3,2,5,5的控制数列是1,3,3,5,5.

(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5，写出所有的{an}；

(2)设{bn}是{an}的控制数列，满足ak+bm-k+1=C(C为常数，k=1,2,…,m).

求证：bk=ak(k=1,2,…,m)；

解析(1)数列{an}为：2, 3, 4, 5, 1；2, 3, 4, 5, 2；2, 3, 4, 5, 3；2, 3, 4, 5, 4；2, 3, 4, 5, 5.

(2)因为bk=max{a1,a2,…,ak},bk+1=max{a1,a2,…,ak,ak+1},所以bk+1≥bk.

因为ak+bm-k+1=C,ak+1+bm-k=C,所以ak+1-ak=bm-k+1-bm-k≥0，即ak+1≥ak.

因此，bk=ak.

(3)对k=1,2,…,25,a4k-3=a(4k-3)2+(4k-3);a4k-2=a(4k-2)2+(4k-2);a4k-1=a(4k-1)2-(4k-1);a4k=a(4k)2-(4k).

比较大小，可得a4k-2>44k-3.

又a4k+1>a4k.

从而b4k-3=a4k-3,b4k-2=a4k-2,b4k-1=a4k-2,b4k=a4k.

(b1-a1)+(b2-a2)+…+(b100-a100)

=(b3-a3)+(b7-a7)+(b10-a10)+…+(b4k-1-a4k-1)+…+(b99-a99)

=(a2-a3)+(a6-a7)+(a9-a10)+…+(a4k-2-a4k-1)+…+(a98-a99)

=2525(1-a).

点评本题通过自定义“控制”数列，考查数列的通项公式、等差和等比数列的基本性质等基础知识，考查数列运算的基本技能以及分析探究和推理论证的能力．

四、自定义距离

例4 已知平面内的线段l及点P，在l上任取一点Q,线段PQ长度的最小值称为点P到线段l的距离，记作d(P,l).

(1)求点P(1,1)到线段l:x-y-3=0(3≤x≤5)的距离d(P,l);

(2)设l是长为2的线段，求点集D={P|d(P,l)≤1}所表示图形的面积；

(3)写出到两条线段l1,l2距离相等的点的集合Ω={P|d(P,l1)=d(P,l2)},其中l1=AB,l2=CD,A,B,C,D是下列三组点中的一组，对于下列三组点只需选做一种．

①A(1,3),B(1,0),C(-1,3),D(-1,0).

②A(1,3),B(1,0),C(-1,3),D(-1,-2).

③A(0,1),B(0,0),C(0,0),D(2,0)．

解析(1)设Q(x,x-3)是线段l:x-y-3=0(3≤x≤5)上一点，则

(2)设线段l的端点分别为A，B，以直线AB为x轴，AB的中点为原点建立直角坐标系，则A(-1，0)，B(1，0)，点集D由如下曲线围成

l1∶y=1(|x|≤1),l2∶y=-1(|x|≤1)；

C1∶(x+1)2+y2=1(x≤-1),C2∶(x-1)2+y2=1(x≥1).

其面积为S=4+π.

(3)①选择A(1,3),B(1,0),C(-1,3),D(-1,0),Ω={(x,y)|x=0}.

②选择A(1，3)，B(1，0)，C(-1，3)，D(-1，-2).

Ω={(x,y)|x=0,y≥0}∪{(x,y)|y2=4x,-2≤y<0}∪{(x,y)|x+y+1=0,x>1}.

③选择A(0，1)，B(0，0)，C(0，0)，D(2，0).

Ω={(x,y)|x≤0,y≤0}∪{(x,y)|y=x,02}.

点评本题自定义“点P到线段l的距离”，考查建立坐标系、点的集合、圆的方程和函数表达式、最小值等基础知识，考查数学语言表达和分析解决问题的能力．

五、自定义性质

例5 若无穷数列{an}满足：只要ap=aq(p,q∈N*)，必有ap+1=aq+1，则称{an}具有性质P.

(1)若{an}具有性质P，且a1=1,a2=2,a4=3,a5=2，a6+a7+a8=21，求a3；

(2)若无穷数列{bn}是等差数列，无穷数列{cn}是公比为正数的等比数列，b1=c5=1，b5=c1=81，an=bn+cn判断{an}是否具有性质P，并说明理由；

(3)设{bn}是无穷数列，已知an+1=bn+sinan(n∈N*),求证：“对任意a1,{an}都具有性质P”的充要条件为“{bn}是常数列”.

解析(1)因为a5=a2，所以a6=a3，a7=a4=3，a8=a5=2．

于是a6+a7+a8=a3+3+2，又因为a6+a7+a8=21，解得a3=16．

an=bn+cn=20n-19+35-n．

所以{an}不具有性质Ρ．

(3)充分性：

当{bn}为常数列时，an+1=b1+sinan．

对任意给定的a1，只要ap=aq，则由b1+sinap=b1+sinaq，必有ap+1=aq+1．

充分性得证．

必要性：

用反证法证明．假设{bn}不是常数列，则存在k∈N*，使得b1=b2=…=bk=b，而bk+1≠b．

下面证明存在满足an+1=bn+sinan的{an}，使得a1=a2=…=ak+1，但ak+2≠ak+1．

设f(x)=x-sinx-b，取m∈N*，使得mπ>|b|，则f(mπ)=mπ-b>0，f(-mπ)=-mπ-b<0，故存在c使得f(c)=0．

取a1=c，因为an+1=b+sinan(1≤n≤k)，所以a2=b+sinc=c=a1，

依此类推，得a1=a2=…=ak+1=c．

但ak+2=bk+1+sinak+1=bk+1+sinc≠b+sinc，即ak+2≠ak+1．

所以{an}不具有性质Ρ，矛盾．

必要性得证．

综上，“对任意a1，{an}都具有性质Ρ”的充要条件为“{bn}是常数列”．

点评本题考查等差、等比数列的性质和三角函数等基础知识，着重考查运用反证法等证明方法进行推理论证的能力．

六、自定义运算

(2)由a2-4b>0知点M(a,b)在抛物线L的下方，

①当a>0,b≥0时，作图可知，若M(a,b)∈X，则p1>p2≥0，得|p1|>|p2|.若|p1|>|p2|，显然有点M(a,b)∈X,∴M(a,b)∈X⟺|p1|>|p2|．

②当a>0,b<0时，点M(a,b)在第四象限，作图可知，若M(a,b)∈X，则p1>0>p2，且|p1|>|p2|.

若|p1|>|p2|，显然有点M(a,b)∈X,∴M(a,b)∈X⟺|p1|>|p2|．

根据曲线的对称性可知，当a<0时，M(a,b)∈X⟺|p1|>|p2|．

综上所述，M(a,b)∈X⟺|p1|>|p2|(*).

综合(*)式，得证．

∵q≤p-1，

点评本题通过自定义“运算”，考查函数的导数、方程求解、不等式、曲线方程及性质等基础知识，考查运算求解的基本技能、分类讨论的思想方法以及推理论证的思维能力．