基于双侧钻臂位姿协同约束的凿岩台车车体定位方法

吴昊骏，龚 敏

(北京科技大学 土木与资源工程学院，北京 100083)

凿岩台车钻孔自动定位是掘进技术发展的重要方向和近年来研究热点[1-4]。钻孔自动定位首先需要解决车体定位(台车与巷道位置关系)问题，车体定位后计算机才能据此确定各钻臂移动参数和实施动作控制[5-6]，因此具有非常重要的作用。

由于产权保护原因国外车体定位文献很少，可供借鉴参考的资料有限。李军利等[7]研究了与台车类似的掘进机车体定位，通过坐标变换矩阵并基于闭环尺寸链进行定位，然而每次掘进前需用全站仪测量的方式较麻烦并影响施工;ELSRUD Rolf[8]介绍了阿特拉斯台车自动定位RCS控制系统，首次提出利用钻臂穿过巷道定向激光的车体定位方法，但文献没有阐述具体解算过程;对此何清华，谢习华等[9-10]详细推导了该方法的计算求解步骤，为我国首台隧道凿岩机器人研发奠定了重要基础，一些学者[11-13]据此进行了相关研究，这也是目前普遍认可的定位方法。但这一方法在实际应用时因堆碴高度变化(现场常见情况)误差很大，采用车体横向角度传感器作补偿，在现场应用时准确性较差。

为解决上述方法无法适应堆碴高度变化的难题，笔者提出双光束双钻臂车体定位的新方法，从理论上证明了车体位姿解的惟一性，给出了车体定位计算求解过程，并在绿水洞煤矿成功实现井下钻孔自动定位工业性试验。

1 双钻臂法与车体位姿惟一性证明

1.1 车体定位问题的理论表述

车体定位即确定台车与巷道位置关系。双钻臂台车如图1所示，左右钻臂对称，各有5个转动轴和1个移动轴。台车停在工作面前适当位置，以设计姿态钻孔，根据台车移动特点建立两空间坐标系如图2所示，坐标系分别为:车体基坐标系{OC}和工作面坐标系{OG}。要求将钻具轴线向量stick在{OC}下的坐标表达实时转换到其在{OG}下的坐标表达，直到其与{OG}内炮孔设计向量hole共线，且当stick末端与hole始端重合时，钻孔自动定位过程结束，可以开始钻孔。图2中坐标系{O0L}和{O6L}，{O0R}和{O6R}分别为按照D-H法[14-15]确定的左侧钻臂首端和末端坐标系，右侧钻臂首端和末端坐标系。

图1 车体结构简图Fig.1 Organization graph of drill rig

各工作循环停车位置是随机的，{OC}和{OG}的关系不固定。钻孔前应以简易办法快速确定本次{OC}和{OG}的变换关系，即车体定位。

1.2 双钻臂法与位姿解惟一性证明

针对原定位法存在的问题，本文提出双钻臂车体定位方法(以下简称双钻臂法):利用已有传感器，增加一路井下定向激光，以台车双侧钻臂同时穿过两束激光进行车体定位。该方法不存在车体双侧定位误差传递问题，且一定程度上可反映工作面左右不平整情况。

下面将分析双钻臂法能否得到车体定位的惟一解，是否可解决车体横向角度变化的问题。

双钻臂法原理如图3所示:提供两束平行激光，在工作面上的投影OL和OR分别作为左侧和右侧激光坐标系{OL}，{OR}的原点。定位过程中{OL}的YL轴和{O6L}的Y6L轴形成角变量θL，{OR}的YR轴和{O6R}的Y6R轴形成角变量θR。在θL和θR的值随机变动的过程中，{OC}的原点OC到激光的距离保持不变(点绕轴转动，点到轴的距离不变)。图3中h为OC到履带底板高度。

图2 车体定位的数学坐标系表述Fig.2 Mathematical description of carriage positioning

图3 新车体定位方法示意Fig.3 New carriage positioning method

此时两侧激光之间距离确定，OC到两侧激光的两个距离不变。则这3个距离将构成一个三边长度已知的稳定三角形。因此求解θL和θR值的问题转化为求解OC位置的问题，并进一步转化为已知三角形两顶点坐标和三条边长，求另一顶点坐标的问题。该问题具有惟一解如图4所示，到OL固定距离的点构成解集A，到OR固定距离的点构成解集B，同时满足两固定距离的解惟一确定为A∩B，因此OC，OL，OR构成一稳定三角形。

图4 真实解的惟一性Fig.4 Uniqueness of true solution

2 双钻臂法公式推导

双钻臂法计算流程如图5所示。

图5 计算流程Fig.5 Process of calculation

以下将根据流程阐述详细计算过程。

2.1 钻臂基坐标系和末端坐标系位姿矩阵

以左侧钻臂为例，基于D-H法在各轴建系{OiL}(i=1,2,…,6)如图6所示，并在激光投影位置建立{OL}，{OC}与{O0L}在车体侧视图内重合。图6中a1,a2,d3,a4,d5,d6为对应位置钻臂的杆件尺寸。首先通过相邻轴坐标系之间的变换关系逐级推导出{O0L}和{O6L}的位姿矩阵。

图6 左侧钻臂连杆坐标系Fig.6 Linkage coordinate system of left boom

沿各轴方向确定各坐标系Z轴，ZiL为{OiL}的Z轴，Z(i-1)L为{O(i-1)L}的Z轴。{O0L}的X0L轴方向人为设定，其余XiL=Z(i-1)LZiL(i=1,2,…,6)，XiL为{OiL}的X轴，按右手法则确定各坐标系Y轴。

按D-H法位姿矩阵通式Ai确定相邻两坐标系(两轴)间的位姿矩阵:

(1)

式中，ai-1，di为连杆长度参数;αi-1，θi为连杆间角度参数;(xiL,yiL,ziL)为点或向量在坐标系{OiL}下的坐标表达;(x(i-1)L,y(i-1)L,z(i-1)L)为点或向量在坐标系{O(i-1)L}下的坐标表达。

式中，A1L为左侧{O0L}和{O1L}的位姿矩阵，…，A6L为左侧{O5L}和{O6L}的位姿矩阵。

设{O6L}在{O0L}下的位姿矩阵:

(2)

式中，(nxL,nyL,nzL)，(oxL,oyL,ozL)，(axL,ayL,azL)，(pxL,pyL,pzL)分别为{O6L}的X6L轴，Y6L轴，Z6L轴，原点{O6L}在{O0L}下的坐标表达。

同理，{O6R}在{O0R}下的位姿矩阵:

(3)

2.2 车体基坐标系和激光坐标系位姿矩阵

设{OC}位于{O0L}和{O0R}中间，三者仅有平移变换而无旋转变换。设平移距离为ε，则{O6L}，{O6R}在{OC}下的位姿矩阵:

(4)

式中，ε为双侧钻臂间距一半，为正数。

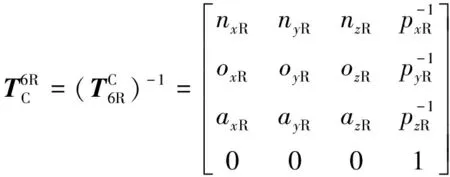
(5)

再考虑与两侧钻具轴线平行的激光。定位过程中为保证平行关系成立，两侧各特制了两枚激光靶，确保OL，OR在{O6L}，{O6R}下的X，Y坐标分别为:(εx,εy)，(-εx,εy)。

θR=0，θL=0时，可得到{OC}在{OL}，{OR}下的位姿矩阵:

(6)

设OC到两束激光距离分别为LL，LR。LL，LR不会随θL，θR取值变化而变化。由式(6)得:

(7)

2.3 解车体基坐标系原点位置

因{OL}，{OR}的ZL轴，ZR轴与{OG}的ZG轴同向，在不涉及Z坐标时，可认为三坐标系的XOY平面共面。设OL，OR在{OG}的XOY平面内的坐标分别为(UL,VL)，(UR,VR)，利用MATLAB编程求解到OL点距离LL，同时到OR点距离LR的点的坐标(U,V)，作为OC在{OG}的XOY平面内的投影点坐标如图7所示(舍去V值较大的解)。

图7 求车体基坐标系原点坐标Fig.7 Find the origin coordinates of the carriage coordinate system

由坐标(U,V)可得车体偏离巷道中线距离E，并根据h计算履带底板下方堆碴高度H。

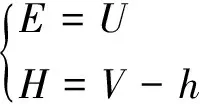
(8)

式中，E为车体偏中距;H为履带底板下方堆碴高度。

2.4 求角变量和车体位姿矩阵

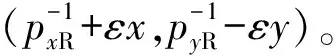
(9)

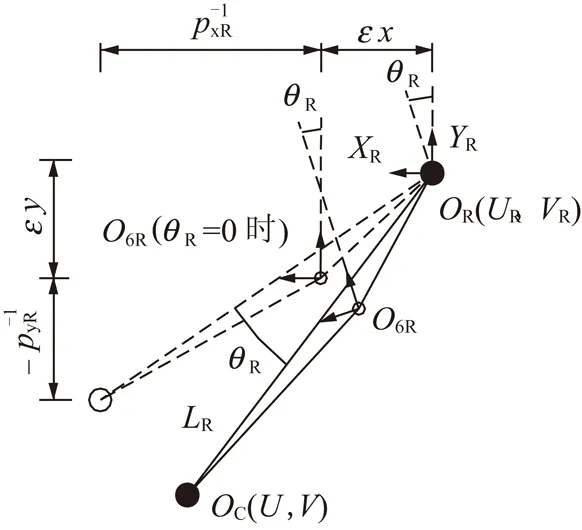
图8 求角变量Fig.8 Calculate the rotation angle

(10)

式中，Rot(ZL,θL)表示绕ZL轴旋转θL所对应矩阵;Rot(ZR,θR)表示绕ZR轴旋转θR所对应矩阵。

(11)

3 车体定位实例

在实验厂房内验证双钻臂法。模拟巷道高3.6 m，宽4.8 m。台车停于工作面前，h=1 256 mm，H=420 mm，稳定后不再移动。分别使用全站仪测量方法和双钻臂法计算车体位姿，将2组结果进行对比。

3.1 全站仪测量车体实际位姿

用全站仪测量车体位姿，在车体四周合适位置设四控制点D,G,E,F如图9所示，线段DG⊥DE且DG⊥GF。DE距巷道中线1 645 mm，与左侧激光指向重合，GF距巷道中线1 580 mm，与右侧激光指向重合。

图9 全站仪测量布点Fig.9 Measuring points of total station

在F点架设全站仪，设置向量FG方向为0角度方向。在车体左右两侧各找一点WL，WR，测得两点坐标为(1.481,2.157,0.969)，(1.490,1.093,0.978)，计算得到E=(2 157+1 093)/2-1 580=45 mm，车体左右翻转角-0.48°。在车体右侧竖直面板上找前后两点W1，W2，测量得到两点坐标为(2.710，1.071，0.873)，(1.587，1.061，0.884)，计算得到前后俯仰角-0.56°。

3.2 建立双钻臂法的位姿矩阵

使用双钻臂法计算车体位姿，根据台车尺寸确定D-H法参数列于表1，尺寸变量单位为mm，角度变量单位为(°)。表1中di，θi两列中θ1～θ5以及d6为轴变量，其值由传感器实时确定。小括号内数据为各轴位于基准位置时变量取值如图10所示。

表1简化机构连杆参数表(右侧)
Table1Linkparametersofsimplifymechanism(rightside)

连杆iαi-1ai-1diθi取值范围1000θ1(0)(-47,14)2-901800θ2(90)(35,106)390532 598θ3(180)(70,320)49000θ4(90)(75,180)590136529θ5(90)(55,135)6900d6(1 739)0(1 739,3 039)

图10 各轴基准位置Fig.10 Reference position of each axis

台车双侧钻臂宽2ε=530 mm;激光靶参数εx=60 mm，εy=120 mm。

车体两侧激光:OL位于{OG}左上方(1 645,1 875)位置，OR位于{OG}右上方(-1 580,1 840)位置。移动双侧钻臂使钻具轴线与激光平行。完成后，两侧各传感器读数为:(-25.840°，-9.624°，0.309°，9.185°，28.330°，1 183.680 mm)，(25.356°，-10.063°，0.369°，9.053°，-28.969°，1 097.002 mm)。

3.3 求车体的位姿矩阵解

MATLAB编程求得OC在工作面上的投影坐标(U,V)=(49.4,1 662.4)，由式(8)得:E=U=49.4 mm，H=V-h=1 662.4-1 256=406.4 mm，与全站仪测量结果吻合。

由式(9)得:θL=3.384°;θR=-1.687°。

根据位姿矩阵求得车体前后俯仰角，左右翻转角为(-0.76°,-0.43°)。与全站仪测量结果基本一致。

3.4 2种定位方法对定位效果影响的讨论

在车体定位参数中，以E和H为例，进一步分析θR，θL变化时，引起的定位参数变化。基准平面设置为H=420 mm，基准偏中距设置为E=45 mm。

以左侧为例，首先计算θL取值不同造成车体位置计算结果与实际结果的差异如图11所示。

图11 角变量和车体位置参数关系Fig.11 Relationship between angle variable and body position parameter

横坐标为θL，θL在0±10°内变化。图11中位置较高曲线表示θL与H的关系;位置较低的表示θL与E的关系。

以H=420 mm为基准面，θL=-10°时对应H=782 mm，二者相差86%;θL=10°时对应H=224 mm，二者相差47%;即使按照θL=0°计算该比例也达到19%。采用双钻臂法计算出θL=3.384°，误差比例为3.3%。

全站仪测得E=45 mm，θL=10°时对应E=85 mm，二者相差88%;而采用双钻臂法计算出θL=3.384°，误差比例为9.7%。

可见θL对车体位置计算结果的影响很大。其中H在后续计算中更为重要。通过双钻臂法将该值误差控制在3.3%，较为可靠。

下面讨论θL变化造成车体定位误差对钻孔定位的影响。假设右侧激光所指位置存在一待钻目标孔。车体精确定位后，按照右侧各传感器读数移动右侧钻臂，钻具末端仍能定位到该位置。当θL取不同值，系统仍按传感器读数进行钻孔定位后，该炮孔实际定位结果与设计孔位的偏离量如图12所示。

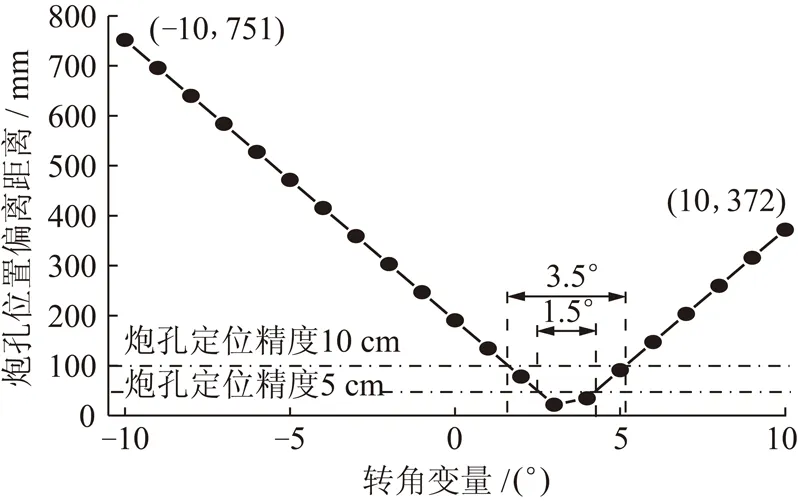
图12 角变量和炮孔位置关系Fig.12 Relationship between angle variable and position of hole

横坐标仍为θL，纵坐标为炮孔定位位置与设计位置距离。θL=-10°时，钻孔定位误差达到75 cm。为控制钻孔定位精度在5 cm以内，θL计算误差应在1.5°内，这在井下清碴很难做到，因此不考虑车体横向转角将对最终钻孔定位精度影响较大，采用双钻臂法则可避免这种情况。

对比采用①全站仪+原方法(左侧定位)和②双钻臂法时的钻孔定位精度(均不进行定位误差补偿)如图13所示。图中2条黑线为①法左右两侧钻孔定位误差结果，红线为②法左右两侧结果，实线为左侧炮孔，虚线为右侧炮孔，因巷道中线上有3孔由左侧钻臂完成，归为左侧孔，故图中实线较长。横坐标代表孔序。

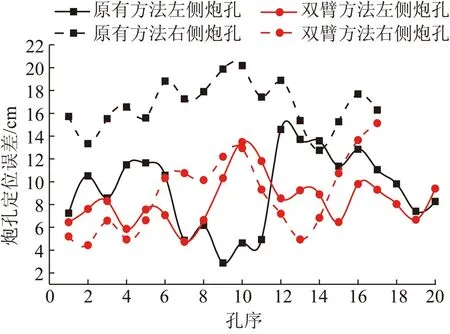
图13 2种方法钻孔定位结果对比Fig.13 Comparison of the results of hole positioning between two methods

由图13可知:原方法两侧炮孔误差明显不同，对侧右侧(虚线)误差比定位侧左侧(实线)误差大，前者集中在12～20 cm，平均误差16.7 cm，后者集中在0～12 cm，平均误差9.3 cm。而双钻臂法任一侧误差均与原方法定位侧误差精度一致，平均误差8.6 cm。

原方法对对侧炮孔存在误差传递并放大的问题。全站仪测量准确的情况下，原方法定位侧炮孔误差精度与双钻臂法双侧炮孔误差精度一致。未补偿前精度均在0～12 cm内。原方法对侧平均误差比定位侧及双钻臂法任一侧平均误差高94%，补偿难度大。

4 结 论

(1)针对原有车体定位方法在工作面堆碴高度变化时定位误差很大甚至无法使用的问题，提出了双钻臂车体定位法，通过数学推导证明了解的惟一性，这一方法已在井下工业性试验得到成功验证，具有普遍性，可用于同类型凿岩台车车体定位。

(2)车体绕激光横向旋转的角变量是求解车体位置参数的关键因素。当横向偏转角为10°时，用过去定位法的车体竖向位置误差达86%。双钻臂法通过准确求解定位过程中的角度值，将竖方向位置误差控制在5%以内，准确度较高。

(3)采用原有方法，为将精度控制在5 cm以内需将车体横向角度控制1.5°以下，这对井下清碴要求很高。双钻臂法不仅从理论上对堆碴高度没有限制，而且将随机变化的堆碴条件转变为求解对象，从定位原理上避免了过去方法的缺陷。

(4)单钻臂定位存在误差向非定位侧钻臂传递的现象，非定位侧炮孔平均定位误差较定位侧高出94%。双钻臂法定位则不存在这一问题，工作面左右两侧钻孔定位精度均在12 cm内，有利于全断面炮孔高效率补偿。