考虑流变特性的两向不等压巷道围岩塑性区近似解
2019-03-27董海龙高全臣
董海龙,高全臣
(中国矿业大学(北京) 力学与建筑工程学院,北京 100083)
巷道围岩弹塑性分析是岩土力学中的一个经典课题。现有的弹塑性理论常以两向等压为条件进行近似求解,这虽简化了计算,但实际工程中的原岩应力场一般为不等压状态,导致其应用具有较大的局限性。对两向不等压巷道围岩进行弹塑性分析,深入了解其塑性发展规律,具有重要的理论和实践意义[1]。
近几年,岩土工作者对这一课题开展了大量研究:马念杰等[2-4]借鉴了早期KASTNER[5]将弹性理论求解的弹性围岩应力解,直接代入塑性条件确定塑性区边界的近似隐式法,深入探讨了两向不等压巷道围岩的塑性区形态。侯公羽等[1]继承并发展了小参数法[6]在两向不等压圆巷围岩弹塑性研究中的运用,使所得摄动解更精确。孙金山等[7-8]在该课题的研究中,则考虑到岩体软化及扩容特性,推导了两向不等压圆巷围岩变形及应力等的近似解。两向不等压巷道围岩的弹塑性问题一般采用诸如以上等近似方法来解决,远没有两向等压条件下的研究成熟[9],各种理论还有待进一步验证和优化。
现有两向不等压巷道围岩塑性区的求解方法[1-13]中,绝大多数将岩石抗压峰值强度视为巷道围岩的峰值应力,鲜有考虑围岩的流变特性。但事实上,巷道开挖后,其周边部分围岩的变形和应力因流变的发展将进一步演化。这一过程异常复杂,但不难想象,围岩达到稳定后的峰值应力不可能高出其一定围压下的长期强度[14];若非如此,不稳定流变必将发生,围岩将继续变形。
为此,笔者以皖北恒源煤矿-950 m进风井井底车场巷道为例,从巷道岩石强度试验出发,分析巷道围岩的力学与变形特性;并引入弹脆塑性模型,就考虑岩体流变特性与否(视围岩长期强度或抗压极限强度为其峰值应力)的2种情况进行对比,得出一些重要的结论。
1 岩石强度试验
皖北恒源煤矿-950 m水平进风井井底车场巷道附近揭露粉砂岩,地质资料显示,巷道顶底板以粉砂岩、砂质泥岩交互为主,累厚均在20 m以上,围岩岩性比较均匀。巷道所处水平已近千米,围岩在高地压作用下的流变较明显。因此,选取该巷道作为本文研究的现场具有一定代表性。
1.1 试验方案与结果
按照有关规定,在对象巷道附近选取岩样,运回试验室进行切割、打磨等加工,制成适量标准岩石试件,并分成I,II两组。
第I组共12个岩石试件,分别进行围压为3,8,13和18 MPa的常规三轴压缩试验,每一围压试验3次,得到较理想的岩石全应力-应变曲线如图1所示。
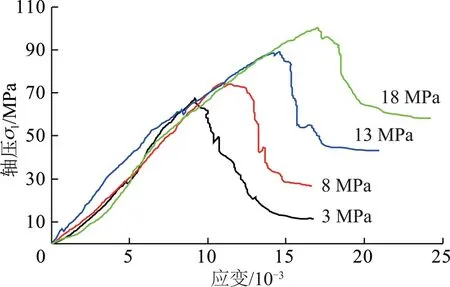
图1 岩石全应力应变曲线Fig.1 Complete stress-strain curves of rock
第II组共16个岩石试件,每4个一小组分为4小组,进行常规三轴蠕变试验。每个小组进行4次试验,试验过程中采用固定围压和改变轴压的方式。围压与三轴压缩试验相对应,分别为8,13和18 MPa,不同围压条件下加载的轴压大小见表1。得到蠕变试验结果如图2所示。

图2 岩石蠕变曲线(围压为3 MPa)Fig.2 Creep curves of rock(confining pressure is 3 MPa)
由图2可知,围压为3 MPa条件下,每次试验岩石试件应变发展到某一值后蠕变基本稳定,蠕变稳定后的应变大小见表1。此外,其余3种围压条件下的三轴蠕变试验情况基本类似,不再赘述,具体情况如图2及表1所示。
表1蠕变终止应变(应力/MPa;应变/10-3)
Table1Creependingstrain(stress/MPa;strain/10-3)

围压/MPa轴压1/应变轴压2/应变轴压3/应变轴压4/应变322/4.90825/5.97628/7.21231/8.940830/5.89233/6.80436/8.13639/9.8521349/8.82052/9.74455/10.77658/12.9721858/10.58461/11.71264/12.94867/14.700
1.2 试验数据处理
根据蠕变终止轨迹理论[10],表1中的数据点(应变,轴压)位于蠕变终止轨迹线上。将其与相应围压下的全应力-应变曲线绘制在同一坐标系下,并对相应数据点进行拟合,得到岩石在该围压下的稳定蠕变终止轨迹,如图3所示,各数据点的拟合度较高。拟合直线与全应力-应变曲线的交点A对应的应力值即为该围压下的长期强度(图3)。

图3 长期强度的确定Fig.3 Determination of long-time strength
重复上述操作,获取另外3种围压下的长期强度(σ∞),连同峰值(σpk)和残余强度(σw),汇总于表2。
表2岩石强度汇总
Table2AggregateofrockstrengthMPa

围压峰值强度长期强度残余强度367.5337.4713.90874.7147.0228.431389.0864.6945.7318100.2976.4363.65
对表2中的数据进行拟合,得到岩石Mohr-Coulomb(M-C)准则的斜直线形包络线,如图4所示。
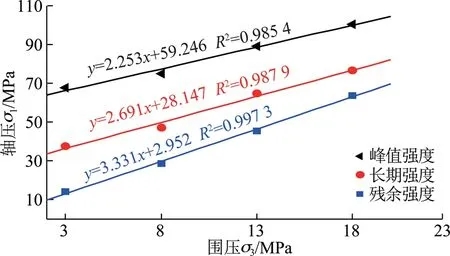
图4 莫尔强度包络线拟合Fig.4 Ftting lines of Mohr’s strength envelope
根据M-C准则可求得抗压峰值强度、长期强度和残余强度拟合直线对应的岩石内摩擦角分别为22.66°,27.27°和32.56°,黏聚力分别为19.74,8.58和0.81 MPa。
2 两向不等压巷道塑性区近似解
2.1 巷道力学模型
恒源煤矿南北及东西方向均存在构造应力,利用JHDC-1型地应力测试系统测得:矿井主要岩石巷道所在的-950 m水平竖向原岩应力为21.78 MPa,水平原岩应力17.424 MPa。即本文所研究巷道处于侧压系数λ=0.8的两向不等压地应力场中。
现有两向不等压巷道围岩塑性区的求解方法[1-9,11-13]中,经常忽略围岩的流变特性。为此,本文引入弹脆塑性模型[15-17](该模型计算简单;且由图1可知,巷道岩石在高围压下的脆性软化特性较明显)将巷道围岩分为弹、塑性区,并建立如图5所示的力学模型,用以分析流变对围岩塑性区的影响。其中,σs和σw为岩石峰值和残余强度,围岩应力达到σs即破裂,并表现为脆性跌落特征,之后进入塑性流动状态。本文旨在探讨流变对围岩塑性区的影响,σs是主要参考指标,考虑流变时,σs为岩石长期强度;否则,为抗压峰值强度。
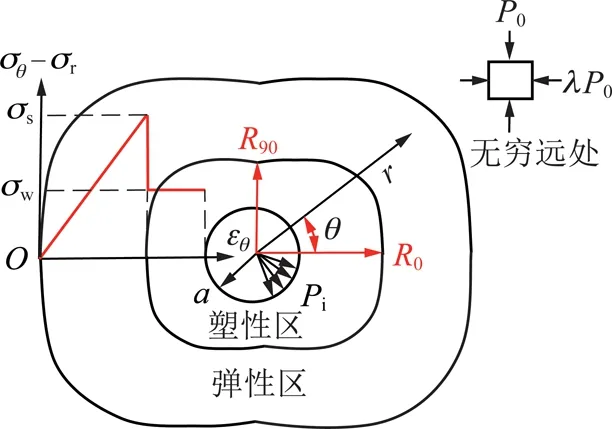
图5 两向不等压巷道力学模型Fig.5 Mechanical model under non-uniform stress field
同时,为了简化理论分析过程,作如下假定:① 巷道围岩连续、均质且各向同性;② 巷道水平布置,圆形断面,长度无限大,埋深足够深;③ 巷道处于两向不等压应力场中,支护体提供均匀支护阻力,不考虑重力梯度的影响。
此外,为便于表述,对模型基本参数作如下规定:a为圆巷半径;r为围岩质点到巷道中心的距离;θ为极角;λ为侧压系数;P0为竖向原岩应力;Pi为支护荷载;R0和R90为水平和竖向轴上的塑性区半径;σr和σθ为围岩径向和切向应力;εθ为切向应变。
巷道围岩出现塑性破坏和破裂时其应力满足M-C准则,可统一表示为
σ1=Aσ3+B
(1)
式中,σ1和σ3为最大和最小主应力;A,B均为材料参数,可由岩体内摩擦角φ和黏聚力C表示。围岩为弹脆塑性材料,φ,C在围岩破裂前为初始值φ0,C0,破裂后为残余值φb,Cb,因此A,B可表示为
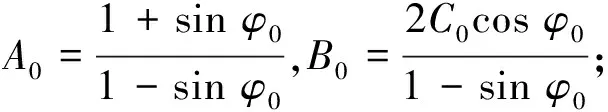
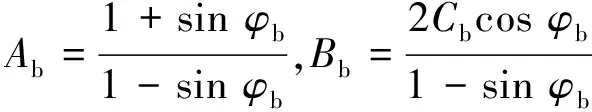
2.2 总荷载不变的规律
为解析两向不等压巷道围岩的塑性区,笔者从力的平衡原理引出总荷载不变的规律作为依据,具体如下。
巷道围岩切向荷载可视为与巷道轴线垂直的平行分布线荷载,简称线荷载,而沿巷道方向单位长度上的线荷载称为线荷载集度(量纲:MT-2)[18]。线荷载集度的大小可用围岩切向应力图像在区间[a,L]内的面积表示,如图6所示;其物理意义是作用在巷道纵向为单位长度,径向深度为L的面积上的荷载大小。
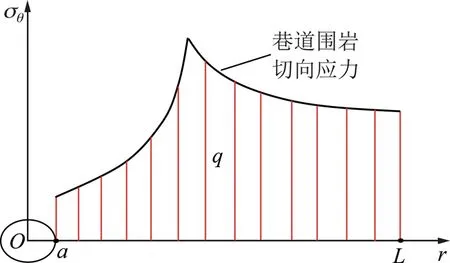
图6 线荷载集度示意Fig.6 Collection degree of line load
根据图6,围岩线荷载集度可表示为
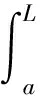
(2)
令L→∞,即为围岩总体线荷载集度(简称为总荷载),记为
(3)
巷道开挖引起围岩应力的二次分布,二次应力分布状态不仅与原岩应力有关,还与围岩力学特性等因素相关。但根据力的平衡原理,不管围岩应力状态如何演变,其总荷载都应保持不变[11]。换言之,不管围岩是否破裂,其总荷载必定等于弹性围岩总荷载。下面以两向等压为条件验证之。
两向等压条件下,若二次应力未达到岩体起塑条件,则围岩仅发生弹性变形,其切向应力为
(4)
故弹性围岩总荷载为
(5)
而以弹脆塑性模型为基础的围岩破裂后的切向应力为分段函数,其总荷载可表示为
(6)
式中,σθe,σθp分别为围岩弹、塑性区的切向应力;Rp为塑性区半径。
λ=1时,以M-C准则为条件,基于弹脆塑性模型的圆巷围岩应力分布及塑性区半径较容易求解,根据文献[17],σθe,σθp和Rp可表示为
(7)
式中,σr|r=Rp为弹性区内边界处的径向应力,σr|r=Rp=(2P0-B0)/(A0+1);N为残余阶段强度参数,N=Bb/(1-Ab)。
将式(7)代入式(6)并联立式(5)可得,巷道围岩破裂后的总荷载Qp与弹性围岩总荷载Qe之差为
ΔQp=Qp-Qe=[N+(Pi-N)(Rp/a)Ab-1-
σr|r=Rp]Rp
(8)
将Rp的表达式代入并化简可得ΔQp=0,这就验证了前述总荷载不变的规律。此外,笔者以经典的轴对称圆巷弹塑性分析(卡斯特纳求解)结果为基础,进行类似的分析,同样可验证这一规律。
而在两向不等压条件下,巷道围岩在水平(及竖向)轴上的剪应力为0,该处的应力依旧满足总荷载不变的规律。下面基于这一规律推导λ≤1(及λ>1)时围岩塑性区在水平(及竖向)轴上的半径。
2.3 R0的近似求解
λ≠1时,若围岩仅发生弹性变形,则其切向应力[13]可表示为
σθ=0.5P0[(1+λ)(1+x)+(1-λ)(1+
3x2)cos 2θ]-Pix
(9)
式中,x=(a/r)2。将θ=0°代入上式,得弹性围岩在水平轴上的切向应力为
σθ0=P0[1+0.5(1+λ)x+1.5(1-λ)x2]-Pix
(10)
故弹性围岩在水平轴上的总荷载为
(11)
围岩破裂后,其应力将出现弹、塑性状态并存的分布特点;且当λ≤1时,R0≠0,即围岩切向应力在θ=0°处存在弹、塑性两种应力状态,如图7所示。
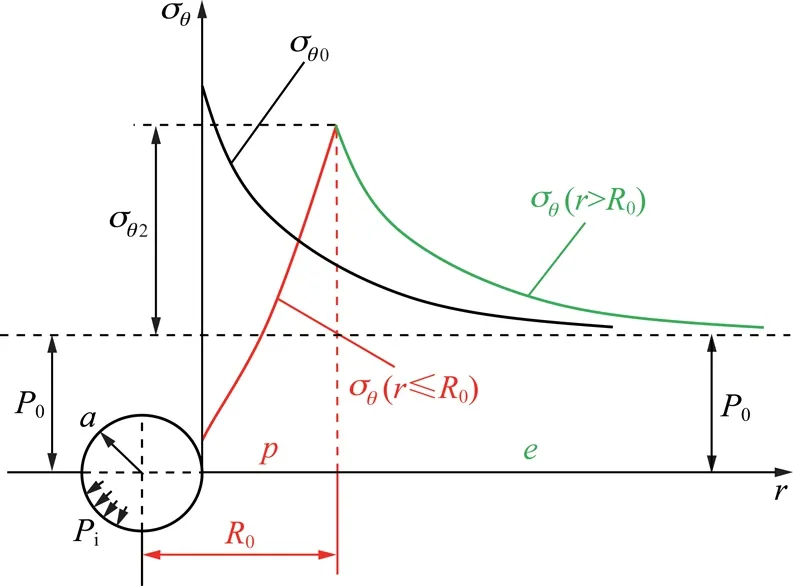
图7 围岩水平轴上应力分析Fig.7 Surrounding rock stress on the horizontal axis
由图7可知,围岩破裂后水平轴上的总荷载为
(12)
式中,σθ(r≤R0)和σθ(r>R0)为围岩塑性区及弹性区在θ=0°处的切向应力。显然,欲求解式(12),必先确定这2个应力的表达式。
巷道围岩在θ=0°处的剪应力为0,这种情况下其塑性区应力仍可利用两向等压情形下获得的应力表达式[9,11-12]。因此,围岩塑性区在θ=0°处的切向应力仍可用式(7)表示,即
σθ(r≤R0)=N+Ab(Pi-N)(r/a)Ab-1
(13)
一般认为[11],弹性区在θ=0°处的切向应力仍然服从式(10),只需以R0替代a即可。应当指出,还须同时以σr|r=R0替代Pi;否则,最终将导致θ=0°时弹塑性交界处的径向应力等于0(本文为支护荷载)[6]。由此得
σθ(r>R0)=P0[1+0.5(1+λ)x0+1.5(1-
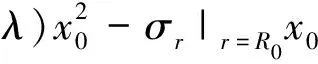
(14)
其中,x0=(R0/r)2;σr|r=R0为围岩水平轴上弹性区内边界处的径向应力,因该处剪应力为0,可将r=R0代入上式并联立准则方程式(1)求得
σr|r=R0=[(3-λ)P0-B0]/(A0+1)
(15)
为具体描述弹性区的σθ~r关系,参照文献[11]将式(14)改写为
σθ(r>R0)=P0+σθ2F(r)
(16)
式中,F(r)是r的某种函数;σθ2的意义如图7所示。
结合式(16)及图7可知:r=R0时,F(r)=1。故将r=R0代入式(14),F(r)=1代入式(16)并联立可得
σθ2=(2-λ-σr|r=R0/P0)P0=b0P0
(17)
式中,b0=2-λ-σr|r=R0/P0。
将式(17)代入式(16)并对照式(14)可得
(18)
故而,弹性区围岩在θ=0°处的切向应力为

(19)
式中,σθ|r=R0为水平轴上弹性区内边界处的切向应力,可将式(15)代入式(1)求得
σθ|r=R0=A0σr|r=R0+B0
(20)
综上,将式(13),(19)代入式(12),并结合总荷载不变的规律联立式(11),(12)可得
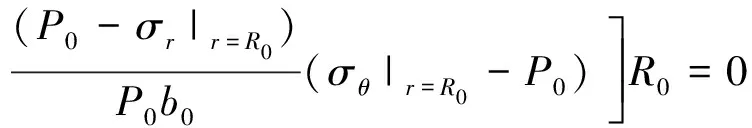
(21)
解之即得λ≤1时R0的近似解为
R0=a[(Δ0-N)/(Pi-N)]1/(Ab-1)
(22)

2.4 R90的近似解及算法的合理性
2.4.1R90的近似解
类似地,λ>1时,R90≠0;且围岩在θ=90°处的剪应力也为0,即R90可经与R0类似的推导得到
R90=a[(Δ90-N)/(Pi-N)]1/(Ab-1)
(23)
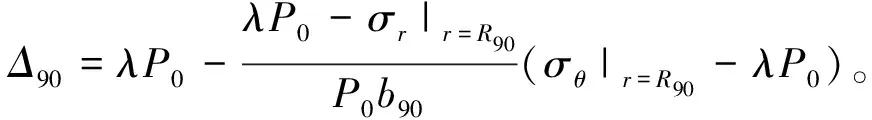
此外,将λ=1代入式(22),(23),并结合λ=1条件下围岩在弹性区内边界处的径向与切向应力之和为2P0这一基本性质可得
(24)
可见,基于轴对称平面应变理论得到的两向等压巷道围岩塑性区的解析半径,是本文算法在λ=1时的特例,这一定程度上说明了本文结果的正确性。
2.4.2 算法的合理性验证
为验证本文算法的合理性,令φb=φ0,Cb=C0(不考虑岩体的峰后软化),则模型退化成理想弹塑性模型。对于该模型,蔡晓鸿[12]已给出围岩塑性区半径的解析表达式为
R=a{(1-sinφ0)[0.5P0(1+λ)+P0(1-
λ)cos 2θ+C0cotφ0]/(Pi+
C0cotφ0)}0.5(1-sin φ0)/sin φ0
(25)
假定P0保持不变,λ=0.3~2.0,并代入本文有关参数对比计算可以发现,本文算法在不考虑岩体峰后软化特性时的计算结果与蔡晓鸿给出的相应解析结果完全吻合,如图8所示。这验证了本文算法的合理性。
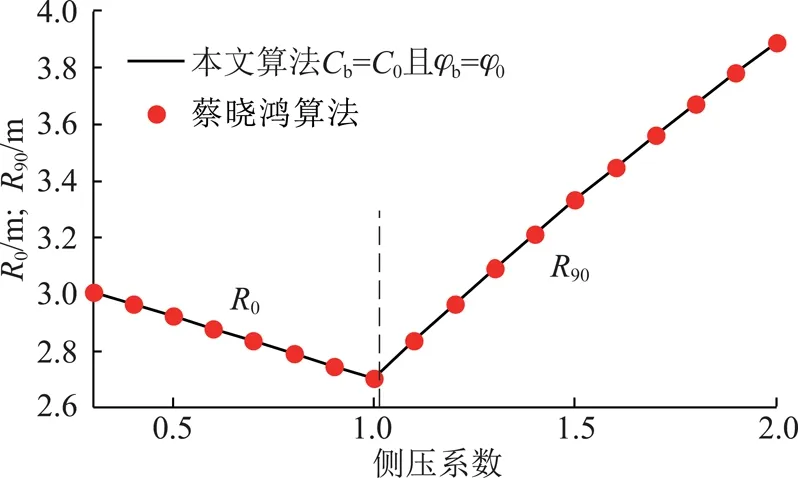
图8 对比分析结果Fig.8 Correlation analysis results
2.5 巷道围岩塑性区半径的近似解
考虑到本文不考虑岩体峰后软化时的结果与蔡晓鸿给出的解析结果完全吻合,故可以以式(25)为基础确定巷道围岩塑性区的形状;再结合上述推导的R0或R90,根据相似原理,可确定两向不等压巷道围岩的塑性区半径为
(26)
式中,R|θ=0和R|θ=90°分别为式(25)确定的围岩水平及竖向轴上的塑性区半径。
3 试验巷道围岩塑性区分析
3.1 试验巷道塑性区现场窥测
为本文理论可靠性的检验提供依据,利用徐州产YDSG-10型号岩层钻孔窥视仪对已基本稳定的对象巷道围岩松动圈进行现场窥视,以帮部位置(距轨道面1.8 m)为例,钻孔窥视截图如图9所示(注:由于现场窥测过程中设备故障,无法显示探头即时深度,因此通过钻孔底部钢卷尺的刻度来确定探头的位置)。

图9 不同深度钻孔窥视截图Fig 9 Borehole view screenshots in different depths
钻孔窥视结果表明,0.6 m产生了较大的破碎,在1.9和2.0 m处附近仍有破碎痕迹,2.0~2.2 m乃至更深部位的钻孔呈现完整原岩的特征,这说明围岩帮部塑性区深度在1.9~2.0 m内。
3.2 试验巷道塑性区理论解析
恒源煤矿-950 m水平进风井井底车场巷道断面为直墙拱形,圆拱半径为S=2.00 m,巷道高度H=3.8 m,根据等效开挖原理[19],其等效圆形断面的半径a=0.5(S2+H2)/H≈2.43 m。巷道围岩其它基本力学参数如下:λ=0.8,P0=21.78 MPa,Pi=0.75 MPa,Cb=0.81 MPa,φb=32.56°。
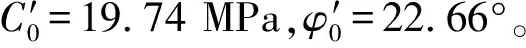
将上述参数代入第2节相应关系式即可分别求出相应的巷道围岩理论数值解。
图10为考虑流变与否的围岩塑性区分布,其表明:若考虑岩体流变,视岩石长期强度为巷道围岩峰值应力,则得到塑性区形状为长短轴相差不大的椭圆形,其半径在3.51~4.05 m内。依据松动圈理论[20],巷道围岩帮部塑性区深度为R0-S(拱半径)=2.05 m,这与现场窥测结果基本吻合。但若不计岩体流变,视岩石抗压峰值强度为巷道围岩最大应力,则所得塑性圈被巷道边界所囊括,即巷道围岩仅产生弹性变形。显然,这与工程实际不符且安全性低,无疑是高估了巷道围岩岩性。可见,在巷道围岩长期稳定性评估及其支护设计中应兼顾岩体的流变,以得到更为合理安全的结论。
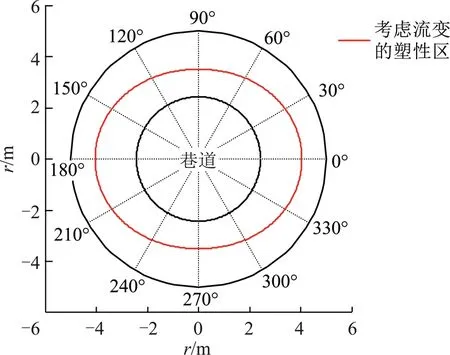
图10 考虑流变的塑性区分布Fig.10 Distribution of plastic zone considering rheology
此外,岩体峰后特性对巷道围岩的塑性区分布也具有重要影响,如图11所示,为考虑峰后软化与否的对比计算结果。由图可知,若不考虑峰后软化,视围岩为金属那样的理想弹塑性材料,则巷道围岩塑性区以“滑动楔形”状分布于两帮较小范围内,围岩塑性区半径在2.43~2.79 m内,巷道帮部松动圈深度仅为0.79 m,围岩几乎仅产生弹性变形,这与工程实际同样相差较大。
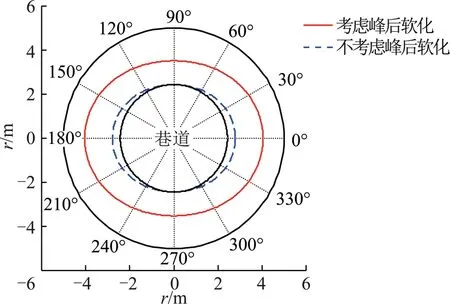
图11 考虑峰后软化与否的对比Fig.11 Constract of considering post-peak softening or not
4 结 论
(1)考虑岩体的峰后脆性软化,以轴对称应力场塑性区公式和总荷载不变规律为基础,推导了两向不等压巷道围岩塑性区边界的近似解,为巷道围岩塑性区的求解提供了一种合理且相对简单的近似算法。
(2)根据轴对称平面应变理论得到的两向等压巷道围岩塑性区的解析半径,是本文算法在λ=1时的特例;同时,本文算法在不考虑岩体峰后软化时的结果,与既有文献给出的相应解析结果完全吻合,这表明了本文算法的正确性与合理性。
(3)巷道围岩的流变和峰后软化特性表现明显,对巷道围岩的变形及应力分布均具有重要影响,在相关理论研究及工程实际中,有必要考虑岩体的流变及峰后软化,以得到更为安全的结论。
