深部软岩巷道高预应力增阻大变形锚杆研究及工程应用
2019-03-27张红军李海燕张太平郭天婵
张红军,李海燕,张太平,王 强,王 薇,王 新,赵 慧,常 涛,郭天婵
(1.山东省地质科学研究院,山东 济南 250013; 2.山东大学 岩土与结构工程中心,山东 济南 250061; 3.山东电力工程咨询院有限公司,山东 济南 250013; 4.吉林大学 地球科学学院,吉林 长春 130061)
随着我国煤炭开采深度的不断增加,大部分煤矿相继出现了不同程度的软岩灾害,据相关文献统计[1],我国每年掘进巷道约6 000 km,深部软岩巷道占28%~30%,而软岩巷道的返修率则高达70%以上,深部软岩巷道稳定控制问题已成为制约我国许多新老矿井向纵深发展的关键性问题之一,急需在新支护材料及支护技术方面取得突破[2]。
锚杆支护是一种主动支护形式,具有经济成本低、支护效果好、成巷速度快等诸多优点,在国内外得到广泛应用,目前已经成为矿井巷道工程的最主要支护形式[3-5]。其主要作用是通过改变锚固范围内岩体峰值强度和残余强度来提高巷道的整体性和稳定性,从而达到加固围岩的目的[6]。大量现场观测资料表明,在进入深部开采阶段后,软岩巷道的变形量较大,一般均大于200 mm,有的甚至可达600 mm以上[7-8]。由于传统锚杆允许巷道围岩的变形量一般均在200 mm以下[9],支护系统刚度小,预应力低,强度不足,抗冲击性能差,已经不能够适应深部巷道围岩大变形破坏特征,常出现因锚杆不能适应巷道围岩大变形破坏而被拉断失效的现象。因此,在研发大变形锚杆方面,国内外学者做了大量的研究工作,取得了一系列的研究成果,比较典型的主要有:ANSELL A[10]在1995 年研制出一种无套管的吸收能量岩石锚杆,平均支护应力达到300 MPa,最大变形量约240 mm;LI C C[11]在2010 年研制出一种新型的可吸收能量的支护装置-D 型锚杆,该锚杆在静力拉伸试验中支护阻力最高达250 kN,最大变形量约60 mm;侯朝炯和何亚男[12]在国外可伸长锚杆的基础上,研发了H型及改进型可伸长锚杆,和普通金属锚杆相比,锚杆的延伸量提高了近400%~500%;何满潮[13-14]基于负泊松比材料研发了恒阻大变形锚杆具有支护阻力大、大拉伸量等优点,在现场应用中取得了良好的支护效果;刘洪涛等[15]基于“高阻让压”原理研发了可接长锚杆,最大延伸量可达685 mm。
同时,随着深部软岩巷道控制理论研究的不断深入,发现预应力是保持巷道稳定性和整体性的关键因素,在支护系统中起着举足轻重的作用[16]。为提高支护系统预应力,康红普等[17]研发了强力锚杆、强力钢带及强力锚索系列材料,有效控制了软岩及回采巷道的围岩大变形;张农和高明仕[18]在分析预应力作用机制的基础上,提出了包括高性能预拉力锚杆、钢绞线预拉力桁架和M型钢带等几种新型实用的预应力控制手段;李海燕等[19]基于深部软岩巷道变形特点,研发了新型高预应力钢绞线锚杆及其配套工艺,该新型锚杆可施加的初始预应力达70~100 kN,具有预应力高、不易松动等优点。
以上学者的研究成果为高预应力大变形锚杆的研发奠定了基础和指明了方向,对深部软岩巷道的控制具有十分重要的意义。本文在以上研究成果的基础上,针对其力学特性和工作机制的优缺点,研发了一种适合深部软岩巷道的高预应力增阻大变形锚杆,该新型锚杆具有“先抗后让再抗,让中有抗,抗中有让,防断增阻”的优良特性,可以施加不低于120 kN的高预应力,让压点可控为180~240 kN,变形量可在150~1 000 mm内灵活调节,锚杆的破断力达到350 kN左右,且在变形的过程当中能保持较高的渐增支护阻力。可以有效控制深部软岩巷道的大变形,保持巷道的稳定性。经现场试验证明支护效果良好,是解决深部软岩大变形支护难题的一种有效途径。
1 高预应力增阻大变形锚杆的结构组成及支护原理
1.1 高预应力增阻大变形锚杆结构
高预应力增阻大变形锚杆,主要由托盘、夹片、杆体1、杆体2、连接套、锥形套、滑移套管等组成(其实物图和剖面图分别如图1,2所示)。杆体1、杆体2和滑移套管的长度都可以根据实际现场需要进行确定,其中杆体1一般不低于400 mm,杆体2不低于700 mm;滑移套管长度宜设置300~1 200 mm,这样可以产生150~1 000 mm左右的变形量,起到大变形的作用;杆体1和杆体2可采用不同直径的钢绞线,本文设计采用的钢绞线直径为17.8 mm,破断力在350 kN左右,可以起到高强支护的作用;锥形套从托盘端头向杆体末端方向逐渐缩小,当岩壁发生大变形时,锥形套在滑移套管内发生滑动,产生滑动阻力;滑移套管直径从托盘端头向杆体末端方向逐渐缩小,可以使滑动阻力呈逐渐增大趋势;托盘通过浇筑形式则实现了传统锚索的托盘和锁具合二为一,不但节省了锚环,大大降低了费用(市场上锚环价格较为昂贵),而且增大了托盘与锁具的接触面积,减少了现场应用中“脱锚”现象的发生;同时对张拉千斤顶进行改造,杆体的外露长度65 mm即可进行张拉,减少了锚杆的外露长度。

图1 高预应力增阻大变形锚杆实物Fig.1 Physical drawing of high pre-stressed increase-resistance large deformation bolt
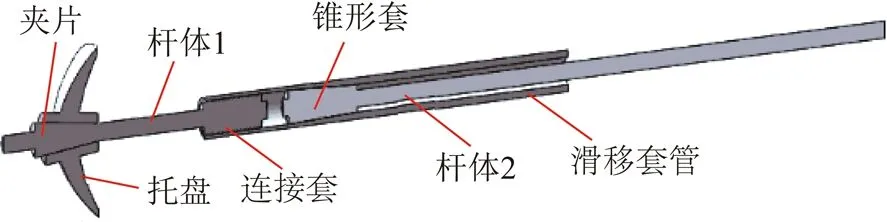
图2 高预应力增阻大变形锚杆剖面Fig.2 Profile drawing of high pre-stressed increase-resistance large deformation bolt
1.2 高预应力大变形锚杆支护原理
进入深部支护阶段后,软岩巷道围岩呈现出变形量大、收敛速率快、持续变形时间长等矿压显现特征,只有在巷道开挖后就及时安装高强度锚杆并施加足够大的预应力,才能有效约束围岩的剪胀变形,避免其强度的迅速衰减。同时锚杆应具有足够的延伸率,允许巷道围岩有一定的连续变形和整体位移。基于此,研发的新型高预应力增阻大变形锚杆支护机理如下:
(1)初支撑阶段:该锚杆安装时可施加不低于120 kN不高于设定让压点的预应力,此时增阻装置内杆体2和滑移套管不会发生相对移动,锚杆依靠杆体材料的弹性变形来抵抗岩体的变形破坏,对围岩形成初期支护强度,该阶段能有效降低离层、滑动、裂隙张开及新裂纹产生等不连续变形的速率,如图3(a)所示。
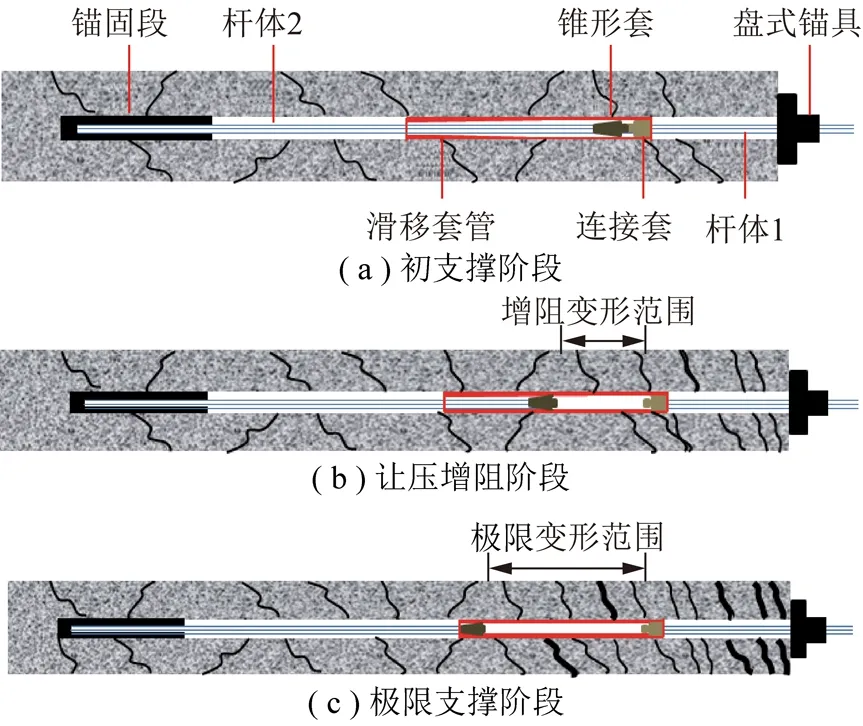
图3 高预应力增阻大变形锚杆支护原理Fig.3 Support Principle of high pre-stressed increase-resistance large deformation bolt
(2)让压增阻阶段:随着围岩压力的继续增大,当达到锚杆设定的让压点后(可根据围岩应力参数对滑移套管内壁弧度变化进行调节,确定让压点),此时增阻装置内锥形体在滑移套管内发生相对滑动,实现大变形让压特性,同时在滑移套管内壁弧度变化过程中呈现增阻特性,形成增阻支护,如图3(b)所示。
(3)极限支撑阶段:增阻装置达到设计的最大变形量后,此时增阻装置内的锥形套和滑移套管停止相对移动,让压装置不再伸长,增阻让压装置变形能得到充分释放。若围岩压力持续增大,杆体会进一步产生一部分极限变形,最大限度的将巷道围岩控于相对稳定状态,如图3(c)所示。
因此,高预应力增阻大变形锚杆和传统预应力锚杆的主要差别就是其具有“先抗后让再抗,让中有抗,抗中有让,防断增阻”的特性。在以高预应力增阻大变形锚杆支护为主的巷道,随着深部巷道围岩发生不断变形,它可以随之拉伸变形,但高预应力增阻大变形锚杆拉伸之后仍能够保持渐增的支护阻力,这种高支护阻力可以有效抵制巷道的继续变形,防止破坏范围的进一步扩大。
2 高预应力增阻大变形锚杆力学特性
为了测试高预应力增阻大变形锚杆的最大延伸量、让压点以及锚杆破断力等特性,在实验室内对该锚杆进行了静力拉伸试验。试验机的基本参数:① 最大荷载1 000 kN;② 试验台高度1 800 mm;③ 位移速率0.2~100 mm/min;④ 加荷速率0.1~20 kN/min;⑤ 最大量程1 100 mm。因实验台量程有限,设计高预应力增阻大变形锚杆总长度为700 mm,其中滑移套管长度为300 mm,采用有一定角度的锥形套和滑移套管使锚杆呈现增阻特性。各试件试验结果相差不大,其中部分试验图片和试验结果如图4,5所示。
由图5可知,试验结果可以较好的反映出高预应力增阻大变形锚杆工作的过程以及性能:在围岩压力为0~222 kN时,为锚杆的初支撑阶段,锚杆通过杆体材料的弹性变形来抵抗岩体的变形破坏;当围岩压力达到222 kN后让压装置开始工作,进入让压增阻阶段,让压量约为113 mm;当围岩压力达到350 kN左右时钢绞线杆体进入极限支撑阶段,随后杆体被拉断,增阻装置未发生破坏。可见,在锚杆总长度为700 mm,滑移套管为300 mm的情况下,高预紧力增阻大变形锚杆的破断力为353.2 kN(刚绞线被拉断),最大延伸量为126.7 mm,总延伸率18.1%。

图4 高预应力增阻大变形锚杆拉伸试验前后对照Fig.4 Control diagram of high pre-stressed increase-resistance large deformation bolt before and after static tensile test
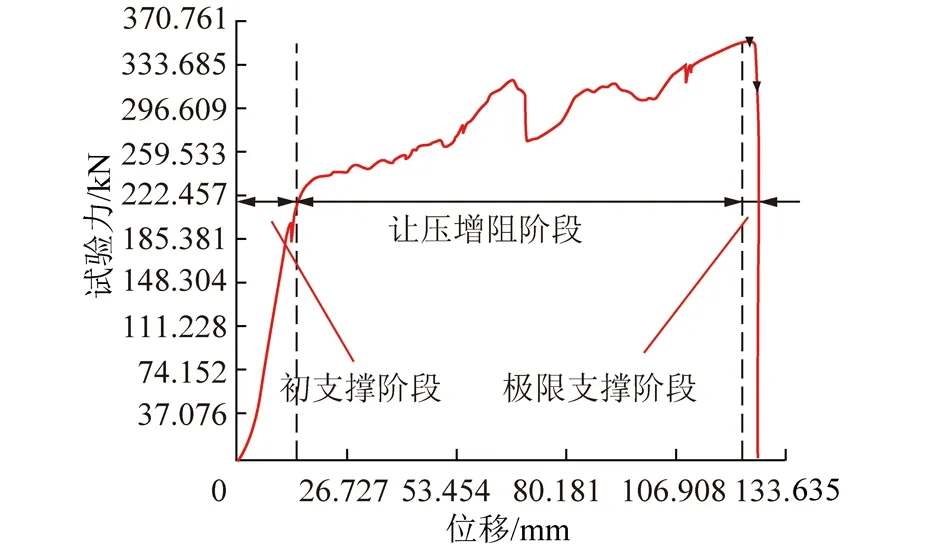
图5 高预应力增阻大变形锚杆静力拉伸试验结果Fig.5 Static tensile test result of high pre-stressed increase-resistance large deformation bolt
为进一步研究不同锚杆长度和滑移套管长度下新型高预应力增阻大变形锚杆的力学特性,在实验室采用简易实验装备(由于上述实验设备量程的局限性),进行不同长度高预紧力大变形锚杆的力学实验,实验数据较上述试验机有一定的误差,但不足以影响试验结果的正确性,试验结果见表1。
表1不同长度锚杆静力拉伸试验结果
Table1Statictensiletestresultofdifferentlengthbolt
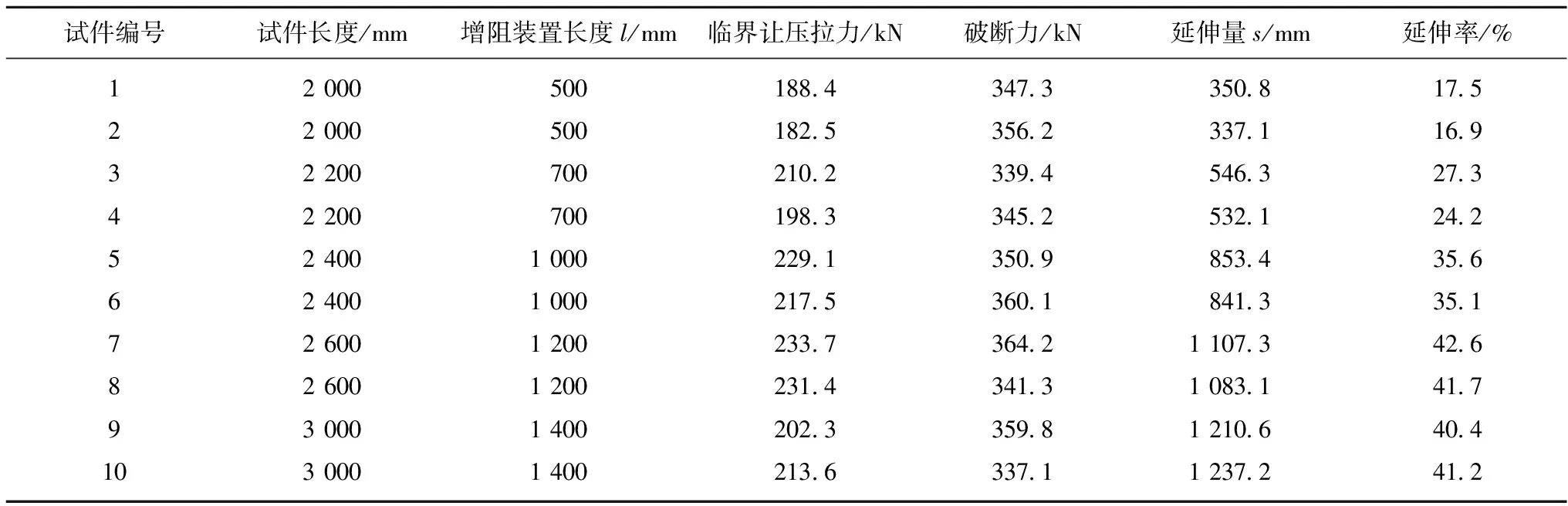
试件编号试件长度/mm增阻装置长度l/mm临界让压拉力/kN破断力/kN延伸量s/mm延伸率/%12 000500188.4347.3350.817.522 000500182.5356.2337.116.932 200700210.2339.4546.327.342 200700198.3345.2532.124.252 4001 000229.1350.9853.435.662 4001 000217.5360.1841.335.172 6001 200233.7364.21 107.342.682 6001 200231.4341.31 083.141.793 0001 400202.3359.81 210.640.4103 0001 400213.6337.11 237.241.2
由表1可知,最大延伸量s和增阻装置长度l基本成线性关系,s=l-(140~200)mm,因此延伸量可以根据实际需要,通过控制增阻装置滑移套管的长度来调整。综合考虑围岩实际变形量及经济因素,锚杆最大延伸量一般可设定为150~1 000 mm,临界让压拉力在180~240 kN内,杆体破断力在350 kN左右。
3 高预应力增阻大变形锚杆数值模拟的实现
数值模拟软件FLAC3D中 CABLE单元可以较为准确地模拟锚杆(索)的轴向锚固效应[20-21],因此本文基于CABLE单元进行二次开发,实现增阻大变形锚杆的数值模拟。
3.1 锚杆杆体轴向拉伸力学模型
根据锚杆拉拔曲线(图5)的三阶段特征,简化并抽象增阻大变形锚杆轴向特性曲线,如图6所示,自由段表达式见式(1),锚固段见式(2)。
(1)
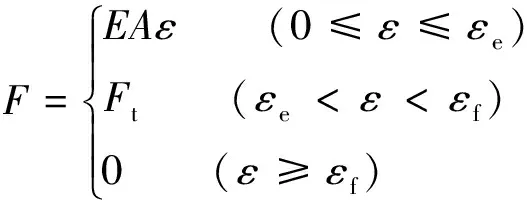
(2)
式中,F为杆体轴力;Fy为锚杆的大变形启动轴力;Ft为锚杆的极限轴力;ε为锚固段杆体轴向应变;εe为锚固段杆体轴向弹性极限应变;εf为锚固段杆体轴向极限应变(由锚杆材质决定);δ为自由段总体伸长率;δe为自由段的弹性极限伸长率;δy为增阻装置的弹性极限伸长率;δf为自由段的极限伸长率,取值方法见式(3);E为锚固段杆体轴向拉伸弹性模量(取钢材弹性模量);E′为自由段等效弹性模量(由试验曲线确定);Ep为让压阶段等效弹性模量(由试验曲线确定);A为杆体横截面积,自由段和锚固段均统一取锚固段杆体横截面积。
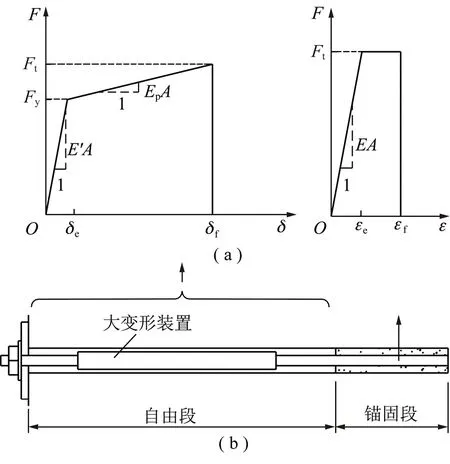
图6 高预应力增阻大变形锚杆杆体轴向力学对应曲线Fig.6 Axial characteristic curve of high pre-stressed increase-resistance large deformation bolt
(3)
式中,lf为锚杆自由段长度,从孔口自外锚固界面的距离;Uy为由锚杆增阻装置和芯体几何参数决定的极限伸长量;δelf为自由段的弹性极限伸长量,往往远小于Uy,因此多数情况下可以忽略。
拉伸初期,锚杆处于弹性阶段;当锚杆轴力达到Fy时(此时锚杆被拉伸到了弹性伸长率δe),锚杆开始进入大变形让压阶段,轴力-伸长量曲线斜率显著降低;当拉伸量达到δf时,锚杆失效,锚杆伸长而轴力保持为0。基于此,将F≥Fy作为锚杆的大变形启动判据,将δ≥δf作为锚杆的破断判据。
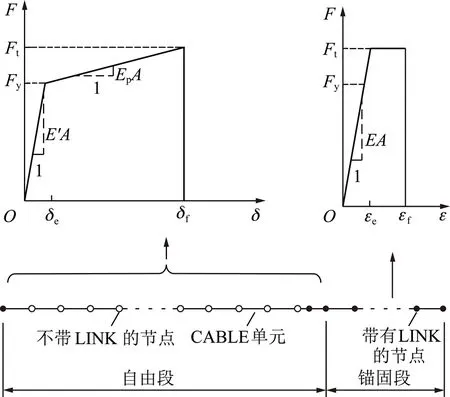
图7 建立的高预应力增阻大变形锚杆数值模型及杆体本构关系Fig.7 Numerical model of high pre-stressed increase-resistance large deformation bolt and constitutive relation
3.2 高预应力增阻大变形锚杆数值模拟实现方法
由高预应力增阻大变形锚杆结构组成及工作原理可知,在锚杆大变形让压过程中,其锚固段的长度伸长量非常有限,大变形实际上是由自由段的伸长贡献的。基于此,以锚杆自由段拉伸本构关系为核心,提出了基于CABLE单元的增阻大变形锚杆数值模型,包括自由段和锚固段2部分,如图7所示。其中,实心圆圈表示CABLE单元节点与围岩之间设置了LINK连接,空心圆圈表示没有设置LINK连接的节点,两节点之间是CABLE单元,自由段内所有节点均不设置LINK连接。
对于自由段,将自由段所有单元作为整体看待;对于锚固段,由于围岩的限制作用,其各单元的受力变形不一致,因此本构关系将针对每一个单元独立设置和运行。一般的锚杆自由段单元的轴力不小于锚固段单元的轴力,而当达到极限轴力Ft时自由段便发生破断,因此锚固段轴力将不会达到极限值Ft,也就更不会破断失效。因此,若无特殊需要,锚杆锚固段可不设破断判据,直接采用自带CABLE单元即可满足要求,减少建模工作量。
3.3 数值模拟程序的实现
以模型中某一根锚杆为例进行说明,不妨设该锚杆自由段共n个单元,由外向内依次为1,2,…,n。
首先进行几何建模,按照FLAC3D正常规则给自带CABLE单元赋予参数:E,E′,A,Fy,设定完成后进入FLAC3D运算主程序。
(1)执行FLAC3D原有的收敛准则,判断计算在程序运行到第i步(i=1,2,3,……)时是否收敛,如果收敛,那么计算立即结束;
(2)如果按照原有的收敛准则,没有收敛,则进入大变形修正及破断修正模块:
① 调用自由段所有单元长度li;
③ 通过多折线等效直线方法实现大变形阶段拉伸刚度:当伸长率达到设定的若干等步距的阶段伸长率时,按照拉伸刚度换算对应的极限拉伸轴力并赋予锚杆;
④ 同时进行锚杆破断的判断:若满足破断判据δi≥δf,令Ei1=0,Ft1=0;若不满足破断判据,则不对参数做任何改动,采用上一步的参数进行下一步运算。
3.4 数值模拟效果验证
试验对象为2.1节所述静拉伸试验锚杆,根据锚杆参数建立的锚杆杆体拉伸试验模型如图8所示,锚杆模型总长0.7 m,划分为14个单元,每个单元长度0.05 m,单元编号(CID)由左向右依次为1~18,其中两端各有1个单元(CID1和CID14)作为夹持段,实际试验锚杆长度为0.6 m(CID2~13)。
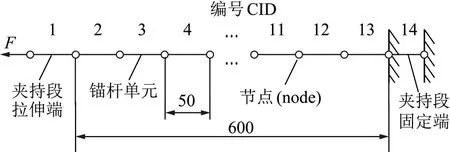
图8 锚杆杆体拉伸试验模型示意Fig.8 Diagram of tensile test model of bolt bar
锚杆单元横截面积A为2.49×10-4m2,自由段弹性模量E′为43 GPa,大变形段模量Ep为2.58 GPa,大变形启动轴力Fy为230.0 kN;极限轴力Ft为350.0 kN;因为锚杆拉伸试验实际上仅针对锚杆自由段展开,因此采用图6(a)所示模型进行赋参数。设定锚杆的极限伸长率δf=0.208。试验时,锚杆右端固定,左端以恒定速度1×10-5m/步的向左拉伸,运行到125 000步时停止计算,查看结果。图9为位移采用最左端节点位移监测值,轴力采用CID2单元的轴力监测值的锚杆拉伸荷载-位移曲线。
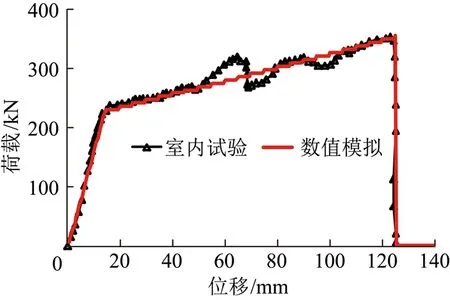
图9 锚杆荷载-位移数值模拟计算结果Fig.9 Numerical simulation result of bolts Load-displacement curves
由图9可知,所建立的锚杆模型受拉伸变形初期轴力与位移基本呈线性关系,当轴力达到230.0 kN时,开始进入大变形阶段,对应伸长量为13.3 mm,与实际基本一致;大变形阶段,轴力增速降低;直至拉伸量达到124.7 mm时,锚杆瞬间破断,轴力降低为0;随后锚杆继续被拉伸而轴力始终为0,呈破断状态直至试验结束。数值试验获得的试验结果与实际几乎完全一致,高精度模拟了大变形锚杆的轴向拉伸力学行为。
4 新型高预应力增阻大变形锚杆工程应用
4.1 工程概况
金阳煤矿位于宁阳煤田东部,矿井主采3层煤,煤层平均厚度6.10 m,煤层倾角7°~11°,设计生产能力21万t/a,其中-500 m疏水巷设计布置在煤层底板以下12~20 m的范围内,巷道埋深537 m,本设计巷道煤层底板岩层尚处在采动影响范围期内。设计断面为半圆拱型,净宽2 600 m,净高2 900 mm,原支护方案采用传统的“锚网喷”一次支护方式:锚杆采用φ20 mm×2 200 mm等强全螺纹钢锚杆,间排距800 mm×800 mm,每根锚杆均用1块MSK2870型树脂锚固剂固定;喷射混凝土厚度120 mm,强度等级C20;金属网采用6 mm钢筋焊接而成,尺寸规格2 000 mm×1 000 mm。巷道开挖后出现了不同程度的破坏,破坏严重地段巷道断面收缩率达到了30%以上,目前巷道处于“前掘后修”的困难支护状态,严重影响了煤矿的正常生产和行人的安全。
4.2 围岩变形特征监测与分析
为详细掌握原支护条件下围岩控制效果、锚杆受力及围岩内部松动破坏范围等情况,通过对巷道围岩的现场监测得到了该巷道围岩矿压显现规律:
(1)巷道变形量大,变形速率快。由图10 围岩变形量监测结果可以发现,在112 d的有效监测期内围岩变形量较大,呈现“两帮收敛量>底臌量>顶板下沉量”的规律,对应的变形量分别为557.9,285.1,223.4 mm。在巷道开挖后的11 d内围岩变形最快,对应的平均变形速率分别为19.1,8.0,14.5 mm/d,8~50 d期间内巷道变形稳定在3~9 mm/d 较快速率增长,直到监测时间为80 d以后,围岩才缓慢进入低速变形阶段,但仍不能确定围岩是否进入稳定期。
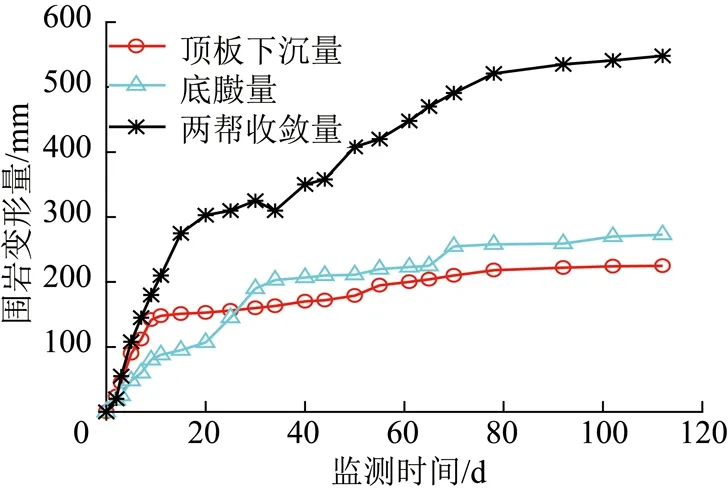
图10 原支护围岩变形量监测结果Fig.10 Surrounding rock displacement monitoring result for original support approach
(2)锚杆初始预应力低,承载能力小。由图11 锚杆受力监测曲线可知,锚杆预紧力较低,最高的仅17.8 kN,左帮锚杆和右底脚锚杆托锚力超过了锚杆的承载极限值,分别在217.3和197.3 kN时发生崩断;而左帮和左底脚锚杆由于预紧力较小,没有充分发挥锚杆的主动支护作用,受力较小;只有正顶锚杆受力状态相对比较稳定。在观测40~50 d之后,为防止软岩巷道进一步变形,矿方进行了二次支护。
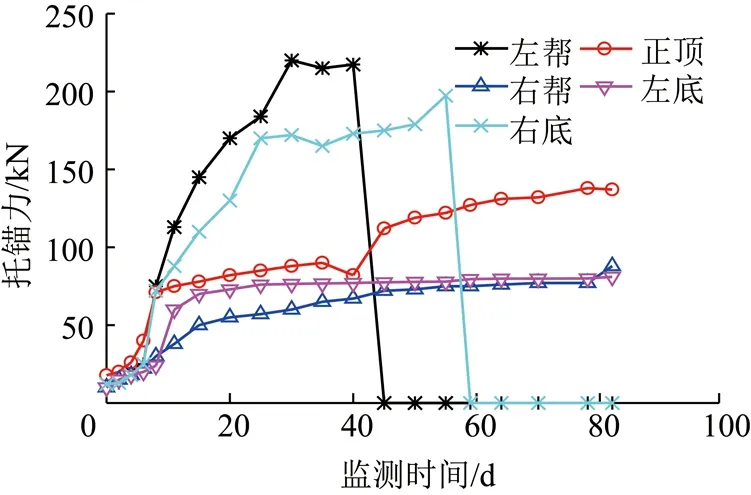
图11 原支护锚杆受力监测结果Fig.11 Force monitoring result of bolt
(3)围岩松动范围大。选用美国劳雷公司SIR-3000地质雷达探测设备对巷道距离开挖面15,30,45,60 m等处的松动破坏范围进行探测,各断面探测结果见表2。由表2可知,围岩的松动范围随距离开挖面距离成逐渐增大的趋势,在距离掘进工作面60 m时巷道平均松动圈范围为1.8 m,最大处已达到了2.2 m,且增长幅度不断加大。
4.3 巷道围岩破坏机制分析
通过对-500 m疏水巷现场监测与分析,综合国内外相似软岩巷道的破坏特征,其破坏原因主要有以下几点:
表2围岩松动圈测试结果
Table2Resultsofsurroundingrocklooseringtest
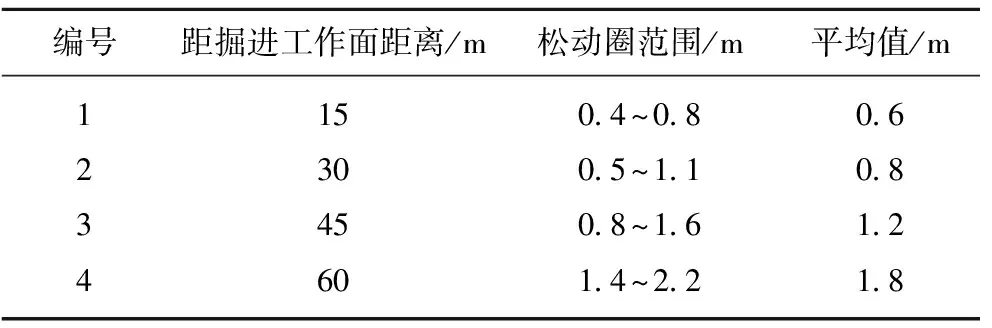
编号距掘进工作面距离/m松动圈范围/m平均值/m1150.4~0.80.62300.5~1.10.83450.8~1.61.24601.4~2.21.8
(1)围岩岩性弱。对-500 m疏水巷顶底板砂岩、页岩、泥岩,通过地质钻机现场取芯,并分别开展三轴压缩试验,得到-500 m疏水巷围岩物理力学参数见表3。由表3可知,巷道围岩4种岩性中,除粉细砂岩力学参数较高外,砂质页岩、中粗砂岩及泥岩的力学参数均较低,砂质页岩的抗压强度只有7.3 MPa,且页岩吸水后易发生膨胀崩解,造成支护困难。
(2)高地应力的影响。根据-500 m疏水巷地应力测试结果,最大水平应力值在15.1 MPa 左右。由于该巷道围岩强度低,巷道一经开挖便处于塑性软化状态,很快将进入“损伤扩容-剪切滑移破坏-碎胀大变形”的失稳破坏模式,属于较为困难支护的巷道类型。
(3)锚杆施加预应力小。通过图11锚杆受力监测结果可知,采用人工扳手对传统的大螺距等强螺纹钢锚杆施加的最大预应力只有设计值(设计值80 kN)的22%左右,严重影响了锚杆的主动支护作用,致使围岩在支护初期就没有得到合理有效地控制,这也是巷道围岩在支护初期就达到较高变形速率的重要因素之一。
4.4 围岩控制对策
基于以上对金阳煤矿-500 m疏水巷围岩变形特征及破坏机理研究结果发现,采用传统的支护方式根本无法解决深部高应力、围岩强度弱以及锚杆预应力低的突出矛盾,必须设法加强支护强度降低围岩的变形速率,同时,提高支护构件适应围岩大变形的能力,才是解决巷道围岩变形的有效途径。因此,结合深部软岩巷道支护“先抗后让再抗”的先进支护理念,提出了以新型高预应力增阻大变形锚杆为核心的支护方案,具体设计参数如下:
表3金阳煤矿-500m疏水巷岩石力学试验结果
Table3Surroundrockmechanicsexperimentresultsof-500mwaterdischarginggatewayinJinyangCoalMine

围岩类型容重γ/(kN·m-3)弹性模量E/MPa抗压强度σ3/MPa抗拉强度σt/MPa泊松比μ黏聚力C/MPa内摩擦角φ/(°)砂质页岩20.33 0507.301.200.311.3221.25中粗砂岩22.65 01023.172.940.282.9524.24粉细砂岩25.68 08643.455.110.253.4628.42泥岩20.82 78014.500.750.302.0922.67
(1)锚杆:全断面采用φ17.8 mm×2 600 mm高预应力增阻大变形锚杆,设计套管长度为500 mm,最大滑移量在300~350 mm,设置锥形套和滑移套管呈一定的锥度,起到增阻变形的效果;每个断面共布置9根锚杆,拱部间排距为1 000 mm×900 mm,帮部800 mm×900 mm;采用MSK2370树脂锚固剂进行端头锚固,锚固长度700 mm;施加预应力不低于100 kN。
(2)金属网:采用6 mm钢筋焊接而成,尺寸规格4 000 mm×1 000 mm,网格尺寸为70 mm×70 mm,网片搭接长度不小于200 mm。
(3)混凝土喷层:采用水泥标号为R42.5的普通硅酸盐水泥,混凝土强度等级C20,喷厚100 mm,其中初喷30~40 mm,混凝土体积比水泥∶砂∶石子=1∶2∶2,水灰比0.4~0.5,砂为纯净的中粗砂,石子粒径3~5 mm。
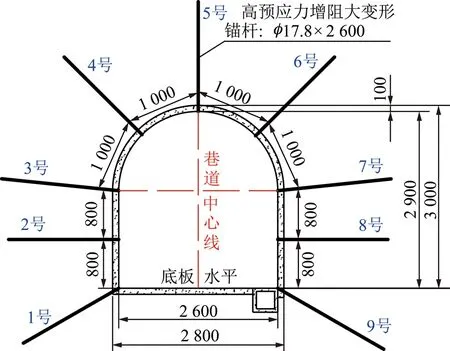
图12 优化后-500 m疏水巷支护断面Fig.12 Optimized supporting section of -500 m water discharging gateway
4.5 数值模拟支护效果及分析
为验证新支护方案的支护效果,对原支护与新支护方案的围岩变形特征进行数值模拟支护效果对比分析。根据金阳煤矿-500 m疏水巷的实际地质条件,选取典型的地质剖面为计算断面。试验采用三维计算模型,各地层均简化为水平,各地层材料物理力学参数依据表3并考虑岩体软化特性综合确定,模型尺寸为高×厚×宽=40 m×1.6 m×40 m。巷道轴向推进方沿z轴为正方向,各地层材料采用BRICK单元模拟,新型锚杆采用本文第3节方法模拟。传统锚杆采用原Cable单元模拟,设定破断伸长率为10%,模型限制两边为水平约束,无水平位移,底部边界为固定约束,地应力施加参数均为实测参数,建立的计算模型及边界条件如图13所示。
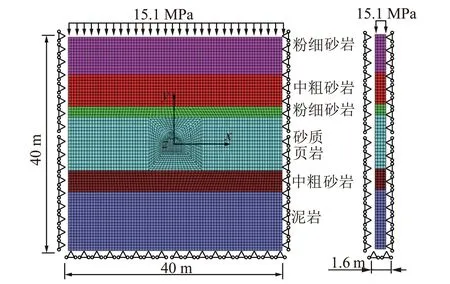
图13 模型及边界条件示意Fig.13 Boundary conditions and model schematic drawing
对比分析图14可知,原支护方案围岩变形量较大,其中顶板下沉量支护方案围岩3个部位的变形量均较大,其中两帮累积变形量达到了550 mm,底臌量与顶板下沉量也分别达到了275和200 mm。采用新型高预应力增阻大变形锚杆支护后围岩变形量明显减小,3个部位的变形量分别为234,100和80 mm,仅为原支护方案的42.5%,36.3%,40.0%。
同时,由于原支护锚杆让压量较小导致两帮锚杆发生了破断现象,而采用高预应力增阻大变形锚杆支护后未发生锚杆破断现象,可见所采用的增阻大变形锚杆的增阻让压效应突出,避免了锚杆因拉伸变形过大而出现破断问题,随着支护阻力的不断增大,不断提高了对围岩的实际控制效果。
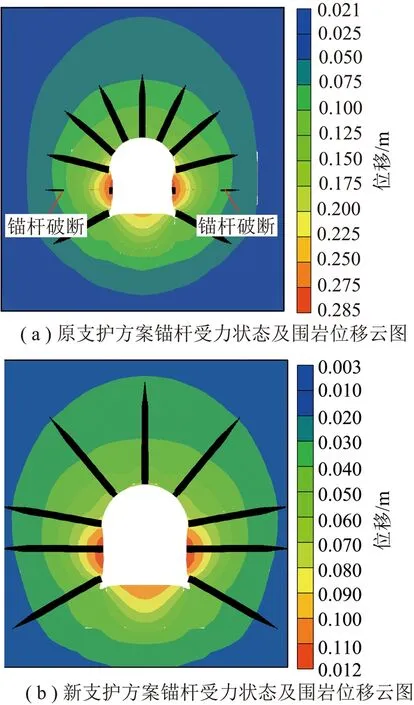
图14 数值模拟计算结果Fig.14 Numerical simulation results
4.6 现场监测结果
为进一步验证高预应力增阻大变形锚杆的支护效果,在新掘的-500 m疏水巷砂质页岩层段进行了现场实验,并对锚杆受力规律和围岩变形量进行了长期监测,监测结果如图15,16所示。
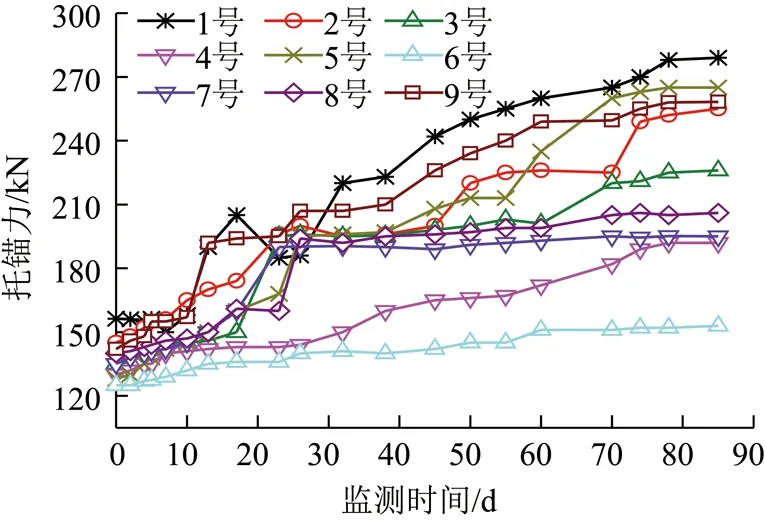
图15 全断面锚杆托锚力监测曲线Fig.15 Force monitoring curves of whole section bolts
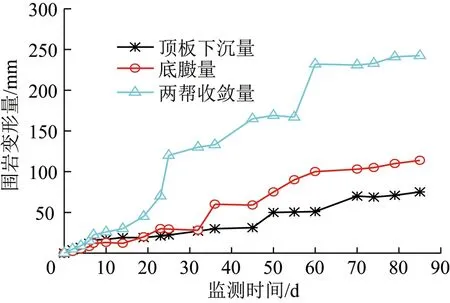
图16 围岩变形量监测结果Fig.16 Deformation monitoring results of surrounding rock
(1)由图15分析可知:① 锚杆预应力均在120 kN以上,其中最高的1号锚杆达到了156.3 kN;② 锚杆受力状态良好,最大值达到278.1 kN,未发生破断现象,到支护后期仍保持较强的支护阻力;③ 锚杆受力呈现阶段性增长的趋势,说明锚杆顺利实现了增阻让压;④ 与原支护方案进行对比可以发现,锚杆受力远远高于原支护方案,高预应力增阻大变形锚杆能够更好的发挥锚杆杆体的支护潜力,对围岩的约束效果更为理想。
(2)由图16分析可知:① 围岩不同部位的变形量均较小,呈现“两帮收敛量>底臌量>顶板下沉量”的规律,分别为242.1,113.9和75.2 mm,相对于原支护方案分别减少了56.6%,60.0%,66.3%;② 在支护初期的14 d内围岩变形速率较慢,说明高预应力有效控制了围岩的初始变形;③ 变形过程呈现阶段性增长趋势,较好的体现了大变形过程中锚杆增阻的效果;④ 高预应力增阻大变形锚杆有效的控制了软岩巷道变形破坏,减少了二次支护甚至多次支护带来的成本增加,起到了一次支护免维修的良好支护效果。
5 结 论
(1)基于深部软岩巷道变形特点,在前人研究的基础上,研发了一种新型高预应力增阻大变形锚杆,室内试验和现场试验表明该新型锚杆可以提供不低于120 kN的高预应力,让压点可控为180~240 kN,变形量可在150~1 000 mm内灵活调节,锚杆的破断力可达到350 kN左右,且在变形的过程当中能保持较高的渐增支护阻力。
(2)建立了新型高预应力增阻大变形锚杆杆体的轴向拉伸力学模型,并基于FLAC3D数值模拟软件,采用Fish 语言编程对其Cable单元进行了相应二次开发,并对该锚杆拉伸过程进行了数值模拟,较高精度模拟了该新型大变形锚杆的轴向拉伸力学行为。
(3)现场矿压监测、室内试验结果表明,金阳煤矿-500 m疏水巷围岩变形速率快、松动破坏范围大,属于典型的深部高地应力软岩巷道。围岩强度低、地应力高以及锚杆初始预应力低是导致其变形的主要因素,采用传统等强螺纹钢锚杆支护已经无法解决三者之间的突出矛盾,必须设法加强支护强度降低围岩的变形速率,同时提高支护构件适应围岩大变形的能力,才能保持巷道围岩的稳定。
(4)针对金阳煤矿-500 m疏水巷围岩变形特征及破坏机理的研究结果,提出了以新型高预应力增阻大变形锚杆为核心的新“锚网喷”技术。数值计算表明,新支护方案能有效提高锚杆受力状态,降低围岩变形量,缩短围岩变形周期。现场应用效果试验监测结果与数值计算结果基本一致,围岩最终变形量相对于原支护方案减少了近60%,取得了良好的支护效果,是一种解决深部软岩巷道大变形难题的新途径。
