应用分层优化法的多协作无人机任务规划方法

杨健 董力勇 王鸿 王龙兴

伴随着无人机在军事与民用领域的成功应用和无人机相关技术的发展,研究人员在不断研究新的无人机使用模式[1].单个无人机通常只能执行单一的、序贯完成的任务.由于无人机具有单机价格低、可扩展性能好的作用,为了更好地发挥无人机的能力,研究人员开始探索多无人机协同执行多个任务的应用模式[2].

多无人机协同作业需解决的技术问题包括任务分配、航迹规划等.任务分配是根据任务环境与各机性能为各个无人机分配任务以保证任务执行的总体消耗最小; 航迹规划是规划出符合无人机机动性能约束和安全要求的最优航迹的问题.在多机协同路径规划领域,已有许多学者做了大量研究,他们的解决方案主要包括数学规划[3]、动态规划[4]、智能优化[5]、人工势场方法[6]等等.数学规划方法能够考虑更多无人机机动性能的问题,但计算效率低.其他方法计算效率较高,但对无人机模型进行了较大幅度的简化.Zhang Yu 等提出了一种单机多目标的轨迹规划方法,他们使用分层解决的方案,先将单机多目标轨迹规划问题建模为一种带有动力学约束的旅行商问题求出初始解,然后利用最优控制的方法求出最终航迹[7].Gu Xueqiang 研究了多无人机多目标的航迹规划方法[8].他们没有深入讨论初始解求解问题.已有的方法中提出应用最优控制方法求解初始解,这种求解模式计算消耗较大[9].

将问题建模为多基地多旅行商问题,首先使用融合Dubins 曲线和B 样条曲线的组合方法规划出所有可选航线,估计每段航线的时间消耗;根据航线规划结果建立了一个加权完全有向图,并应用多基地多旅行商问题求解方法求出对每个无人机的任务分配序列;然后使用航迹规划算法,根据每个无人机执行任务的序列,规划出考虑无人机的机动控制方法的航迹.还提出使用组合B 样条和Dubins 曲线算法规划得到的初始航线作为下一层使用最优控制方法规划精细航迹时的初始解.应用仿真实验验证了提出的方法.

后续的内容如下：在第2 部分中构建了多无人机多目标协同航迹规划模型,第3 部分提出了多无人机任务规划模型,第4 部分进行了仿真实验,在第5 部分给出了最后的结论.

1 多无人机多目标协同航迹规划问题建模

1.1 无人机动力学模型分析

在地面东北天坐标系o-xyz下,无人机的质点运动学模型为：

在航迹坐标系Ok-xkykzk下,飞机的质点动力学方程为式(2)：

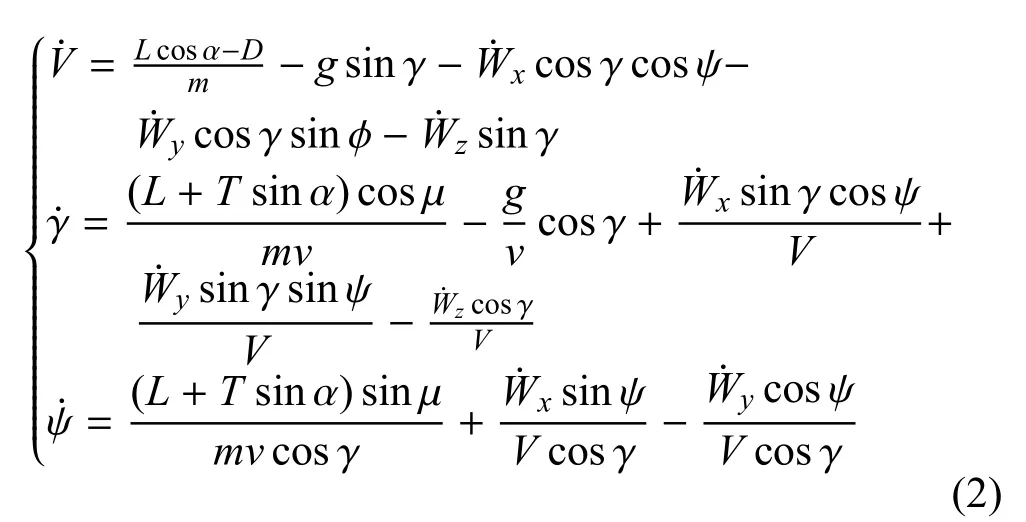
式中,(x,y,z)为飞机空间位置坐标,m为飞机质量;g为重力加速度.V为相对空气的速度大小(真空速),γ 是俯仰角,ψ 是航向角,α 是迎角,µ为滚转角.(Wx,Wy,Wz)为风速沿着坐标轴的分量,为风力加速度沿坐标轴的分量.T,D,L分别是发动机的推力,阻力和升力.描述无人机运动的状态变量为X=(x,y,z,V,γ,ψ),控制无人机运动的控制变量为u= (α,µ,T).其中在实际的控制中发动机推力大小通常是由油门δ 来控制的,因此无人机控制量可以进一步改写为u=(α,µ,δ).

1.2 约束条件

1)起始状态约束

考虑环境中无人机个数为N,无人机Ui,i≤N在初始阶段的状态约束为：

2)过程约束

飞机在飞行过程中主要考虑的要素包括：飞机的平台能力限制,飞行的安全性等要素.无人机飞行时需要保证自身系统的安全稳定,在飞行过程中将飞行包线约束简化为约束条件：

通过两个阶段的计算规划飞机的飞行航迹,在航线规划时考虑飞机的运动性能限制为最小转弯半径,Ui的水平面和铅锤面的最小转弯半径分别为：

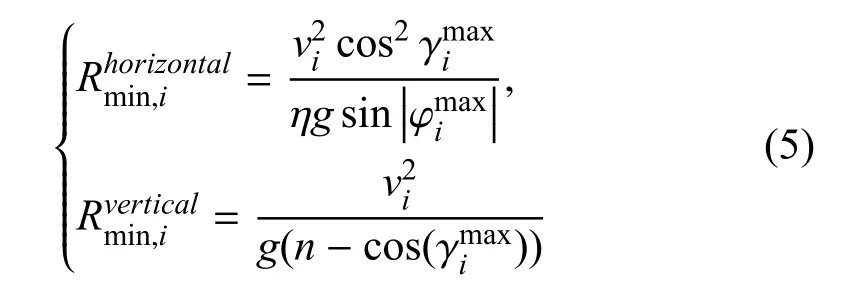
Ui在空中可能遇到威胁或障碍.为了保证飞行安全需避让这些区域,假设威胁与障碍的包络以定位点为球形,以影响距离为半径的半球形.将固定障碍与威胁统一视作障碍,假设环境中有m个障碍,无人机飞行约束条件为,∀j∈m.

式中,Pi是Ui的位置信息,Pjo是障碍Oj的位置,Rio是障碍Oj的半径,‖ ‖为二范数.

3)终端状态约束

无人机终端状态约束为：

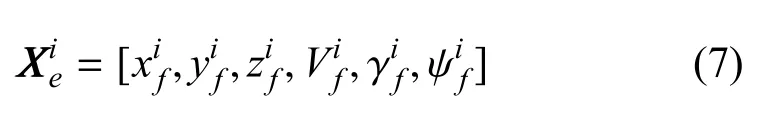
1.3 多协作无人机多任务航迹规划模型

多无人机多目标协同航迹规划需解决多无人机任务分配与航迹规划的问题,其目的是降低无人机的飞行消耗,提高整体任务收益,保证飞行安全.按照根据两层次规划解算的机制,首先将任务分配问题建模为多基地多旅行商问题.为了确定每个旅行航段的消耗,应用航线规划方法规划出一条能够满足始末状态约束、避障约束、机动性能约束的飞行航线,以逼近拟合无人机在这段航段的实际消耗时间或油耗.进而采用成熟方法求解多基地多旅行商问题,确定每个无人机的任务分配与任务执行顺序.在确定每个无人机需执行的任务后,采用航迹规划方法规划其各个航段的航迹.航迹规划阶段将无人机航迹规划问题建模为最优控制问题,并应用数值优化方法规划飞机的航迹.

首先讨论多无人机执行多任务的任务分配问题.由于无人机具有非线性的动力学和避障约束,因而多机多目标作业问题可被建模为带动力学约束的多基地多旅行商问题[7].应用图论方法分析多无人机任务分配问题.假设任务数为nt,因此可将进入点、目标点和退出点统称为节点→Vi,i=1,··· ,2N+nt.从一个节点到另一个节点的有向边记为e(→Vi,→Vj),i≠j,有向边的代价为je= (x(→Vi),x(→Vj)).带有动力学约束的多基地多旅行商问题可以表示为N架无人机分别从各自的预定进入点出发,按照一定的顺序访问各自的节点且他们遍历所有的任务点,然后从各自的预定退出点退出,如图1所示.目标是确定每个无人机的任务及任务序列以最小化总体代价.每架无人机的访问代价为ji,所有无人机访问完所有节点的代价之和为总代价J.

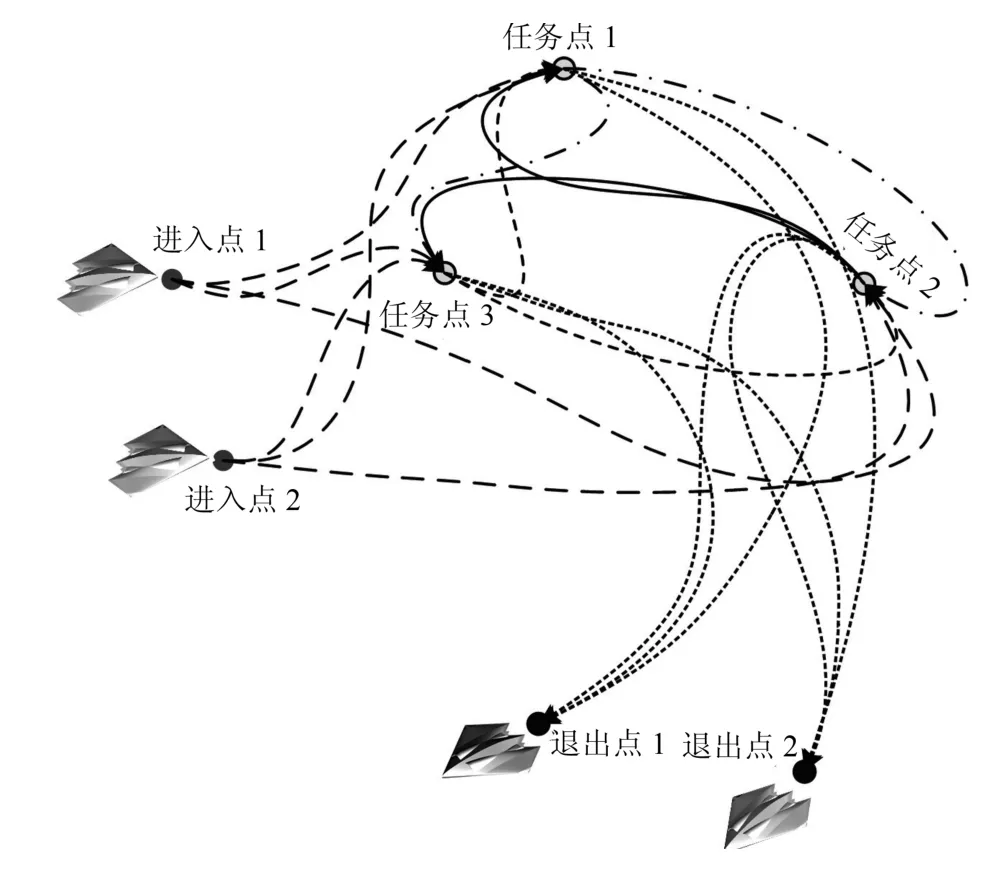
图1 两无人机执行3 个任务构成的多基地多旅行商问题图示

无人机进入点、执行任务点及退出点的姿态是已确定的,无人机始末状态约束为：

目标函数的设定遵循“最小化所有旅行商的总代价+最小化所有旅行商中最大的旅行商代价”的原则,如式(9)所示.此原则能够有效降低任务的代价,同时降低单个旅行商的旅行代价.

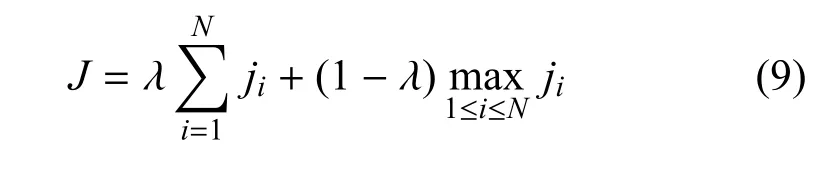
其中,λ 确定了所有无人机总消耗与消耗最大的无人机的消耗在最终的优化目标中所占权重.式(9)优化问题的解应满足式(4)、式(6)与式(8)中的约束.

2 多无人机任务规划问题求解

为了降低多无人机完成多个任务时的总机动消耗,需确定无人机在环境中由任意的退出点到任意进入点的消耗,如图1所示.然后根据无人机执行各个任务的消耗选择能够使总体消耗最小的任务分派.在确定无人机数N与任务数nt时,需要计算A2nt+2 ∗N∗nt条潜在可选航线的消耗,因此,总的计算量较大.由于应用最优控制方法的航迹规划方法计算消耗较多,如果应用航迹规划算法精确规划各段飞行航迹将会导致难以接受的计算量.

本文提出应用融合B 样条与Dubins 曲线的构造式方法规划无人机在各个阶段的飞行航线.在确定各段航线消耗后可以将多无人机多任务的任务分派问题建模为多基地多旅行商问题,应用多基地多旅行商问题的成熟求解方法确定无人机的任务分派,确定每个无人机执行的任务及顺序后采用航迹规划方法规划无人机满足各种约束的航迹.为了保证问题求解的一致性,应用融合B 样条与Dubins 曲线规划无人机航线时以最小化各个航段的飞行时间为目标,在应用最优控制方法规划无人机航迹时也是以最小化任务执行时间为优化目标.

2.1 应用B 样条曲线与Dubins 曲线规划无人机航线

航线规划是规划一条满足无人机性能约束和安全避障需求的曲线的过程.规划航线只考虑无人机的机动性能约束而不需要精确确定无人机在航线上各个航点的控制量,因此其计算量较小.

图1所示有向图包含的有向边由以下几类组成：从进入点到其他所有节点簇(不包括退出点)的有向边,从其他节点簇(除进入点)到退出点的有向边,从每个任务点到其他任务点的有向边.为了确定这些有向边的飞行时间耗费,需要规划出以时间消耗为优化目标的飞行航线.

假设无人机的速度固定不变,则从起始点到终止点距离最短航线的时间消耗也最短,航线规划需要考虑多个要素.一是飞行安全,航线应当规避障碍区域; 二是无人机的始末点约束和机动性能约束问题.B 样条曲线是通过控制点进行设计的,由一组B样条基组成的参数曲线,它优秀的连续特性以及单个控制点不改变远处曲线形状的特点使其在路径规划领域获得了广泛的应用[4],可通过优化调整B 样条的控制点规划出一条保证无人机绕过障碍的距离最短的连续航线,但B 样条算法在进行优化时不能考虑无人机的始末状态约束.根据Dubins 曲线的理论,两矢量间的最短路径由圆弧及其切线组成,其中圆弧与切线的一种组合为“CLC”,路径形状“CLC”是两段圆弧,中间用其切线连接起来.如果圆弧的半径满足无人机的最小转弯半径约束,则圆弧和连接它们的切线拼接的路径是最低阶数曲线中消耗最小的路径[10].本文融合Dubins 曲线与B 样条曲线解决带有姿态约束的航线规划问题[11].“CLC”中间的“L”航段应用B 样条曲线来代替,从而设计出“CBC”曲线.具体算法如下：

已知：无人机的初始状态XXXio及目标状态XXXie及环境中的障碍集信息O.

Step 1.根据无人机的状态计算中间阶段的运动方向,包括俯仰角与航迹偏角;

Step 2.应用Dubins 曲线规划无人机初始点到中间状态的航线以及中间状态到终点状态的航线;

Step 3.应用基于B 样条的非线性优化方法规划无人机在中间飞行过程的飞行航线[12];

Step 4.将3 段航线拼接起来进行平滑获得构造规划的初始状态到终点状态的航线.

中间阶段飞行状态确定为：从初始点到终点的飞行方向.

当前已有较成熟的基于B 样条的航线规划算法,应用“CBC”曲线能够快速规划出各段航线,规划获得的航线的时间消耗为任务执行的消耗.在构建如图1所示的加权有向图后将多无人机任务分配问题转化为多基地多旅行商问题,应用成熟的多基地多旅行商问题求解算法求解无人机的任务分派.

2.2 使用Gauss 伪谱法生成精细航路

在确定无人机的任务序列后需规划满足无人机机动性能约束的具体航迹,无人机飞行航迹规划问题可被建模为最优控制问题.高斯伪谱法是由Benson 在2005年提出的一种优化方法,高斯伪普法求解思路为：将未知的状态时间历程与控制时间历程在一系列高斯点上离散,利用这些离散的状态和控制分别构造Lagrange 插值多项式,逼近真实的状态和控制时间历程,并将动力学微分方程转化为一系列代数约束,最终转化为一系列代数约束的参数优化问题[13].张煜等研究了应用高斯伪谱法规划单个飞机实施空对地行动时的航迹规划问题并取得良好的效果[7].

高斯伪谱法将连续最优控制问题转化为离散参数优化问题,也就是非线性规划(NonLinear Programming,NLP)问题,其标准形式为：

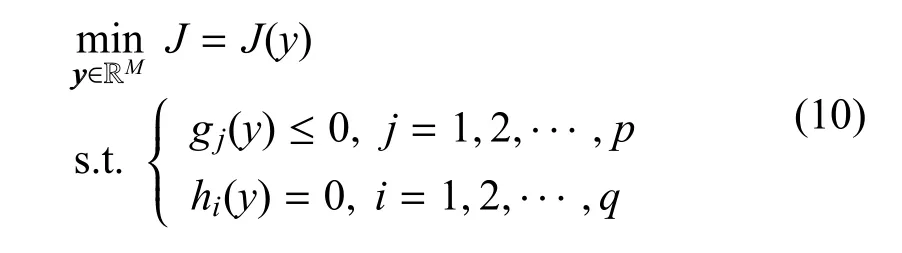
其中,决策向量y包括状态变量X(τi)(i= 0,··· ,N)、控制变量u(τi)(i= 1,··· ,N)、终端时刻tf.J(y)为需要优化的目标函数,本文设置优化目标为最小化无人机飞行每段航迹的飞行时间.p为总的不等式约束条件数,q为等式约束条件数.

应用高斯伪谱方法虽然能够求解出无人机的航迹,但在很多情况下存在着计算量过大的问题,同时高斯伪谱法的求解效果对初始解的依赖程度较高.为了提高高斯伪谱方法计算的效率,本文应用在第一阶段航线规划获得的航线提高初始解计算效率的方法.

以往的研究中对应用高斯伪谱法时的初始解讨论不多,这是因为在这些问题中初始可行解容易找到,例如空天飞机的飞行航迹规划[14],登月过程的航迹规划[9].较为理想的初始可行解能够大幅提升后续优化计算的效率[15].在规划无人机航迹问题中需要考虑更多的约束条件,包括无人机始末姿态约束、避障约束等.鉴于这些约束是非凸约束,不可行的初始解可能导致规划计算低效,甚至无法获得优化结果.

应用“CBC”方法得到的航段使无人机飞行路径最短(也就是时间最短)且符合无人机飞行状态约束与避障约束的航线.因此,在第二阶段优化无人机的飞行航迹时以第一阶段规划得到的无人机航线作为初始解提高航迹规划的计算效率.

3 仿真实验

在PC 机上进行仿真实验以验证算法有效性,算法在Matlab R2014a 环境下编程实现.Tomlab 优化包中有高斯伪谱法优化算法,因此,实验应用Tomlab优化包作为轨迹规划器,应用LKH 求解包求解多基地多旅行商问题.无人机的仿真模型采用“Storm Shadow”UCAV,设计了两个无人机协同执行3 个目标侦察监视任务的场景.为了完成对3 个目标点的侦察监视任务,分别确定了3 个适合进行传感器观察目标的任务点,如图2所示,任务相关的基本数据如表1所示.进入点、退出点与任务点的信息包括：经度、纬度、高度、方位角、速度、航迹倾角.描述障碍的信息包括：经度、纬度、高度、障碍球作用半径.

表1 两无人机进入任务环境状态约束信息

表2 两无人机离开任务环境状态约束信息

表3 任务点状态约束信息

表4 环境中障碍信息

根据无人机的机动性能确定无人机的机动性能约束如表5所示.

表5 无人机机动约束信息

图2描述了两无人机协同执行任务的环境,红色矩形点标识飞机的进入点,绿色矩形点为退出点,蓝色三角为需要观察的目标所在位置,红色空心圆点为通过采样点得到的合适的无人机观察目标的任务执行节点[7].应用本文的规划方法进行规划得到无人机的飞行航迹如绿线和红线所示,绿色的曲线为结合Dubins 曲线与B 样条曲线规划的完整的初始航线,红色航线为应用高斯伪谱法规划的无人机飞行航迹.

两个无人机的运动角度(γ,ψ)如图3所示,飞机执行任务各阶段飞行航迹较稳定,没有较大幅度的波动.在飞行的过程中无人机的俯仰角有一定幅度的变化,但变化幅度如表5所示,在状态变量的约束范围内.

无人机飞行过程中的速度变化如4 所示.无人机的速度在250 m/s 附近变动.由于规划目标是飞行时间最短,因此,无人机会在各航线的飞行阶段通过调整飞行高度将势能转化为动能以加速.由于在每个节点阶段无人机的速度限制是250 m/s,因此无人机会在即将到达目标点时快速减速.在飞行的过程中速度变动的范围没有超过飞机的速度限制.

仿真实验表明,应用分层优化法能够有效完成多无人机多目标协同作业的任务分配与航迹规划.

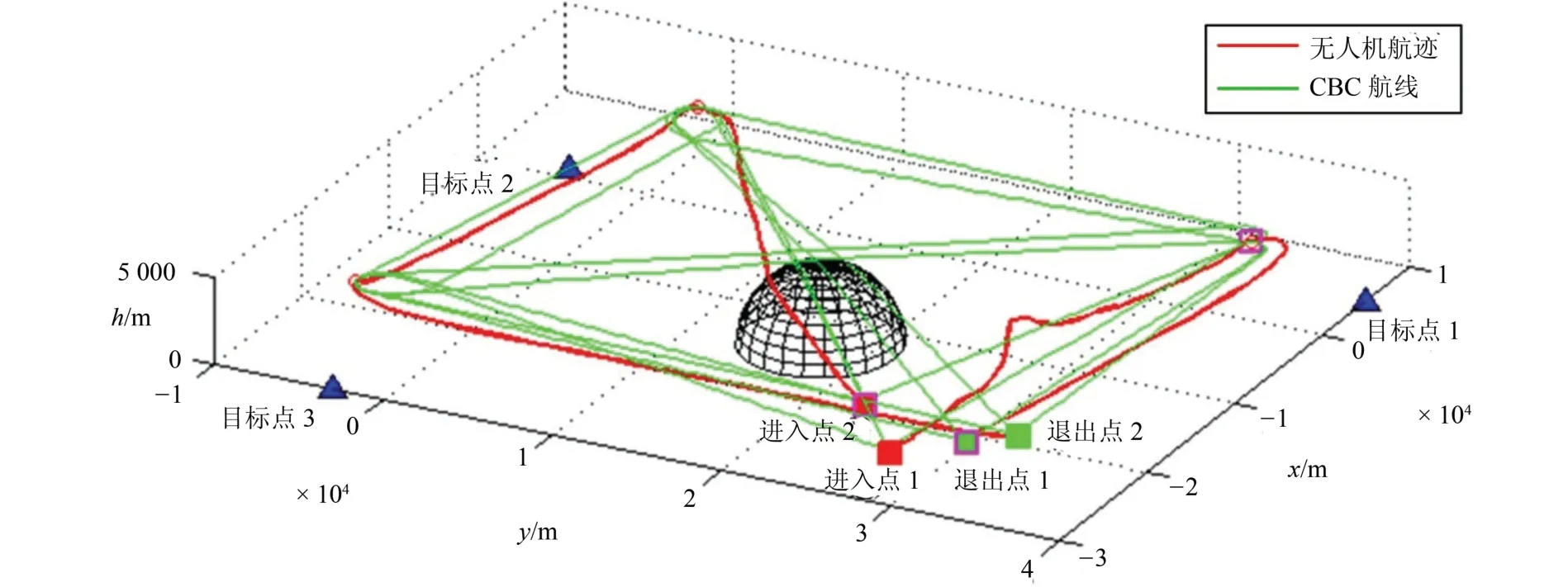
图2 两无人机协同任务分派与航迹规划结果

图3 飞行角度随时间变化曲线

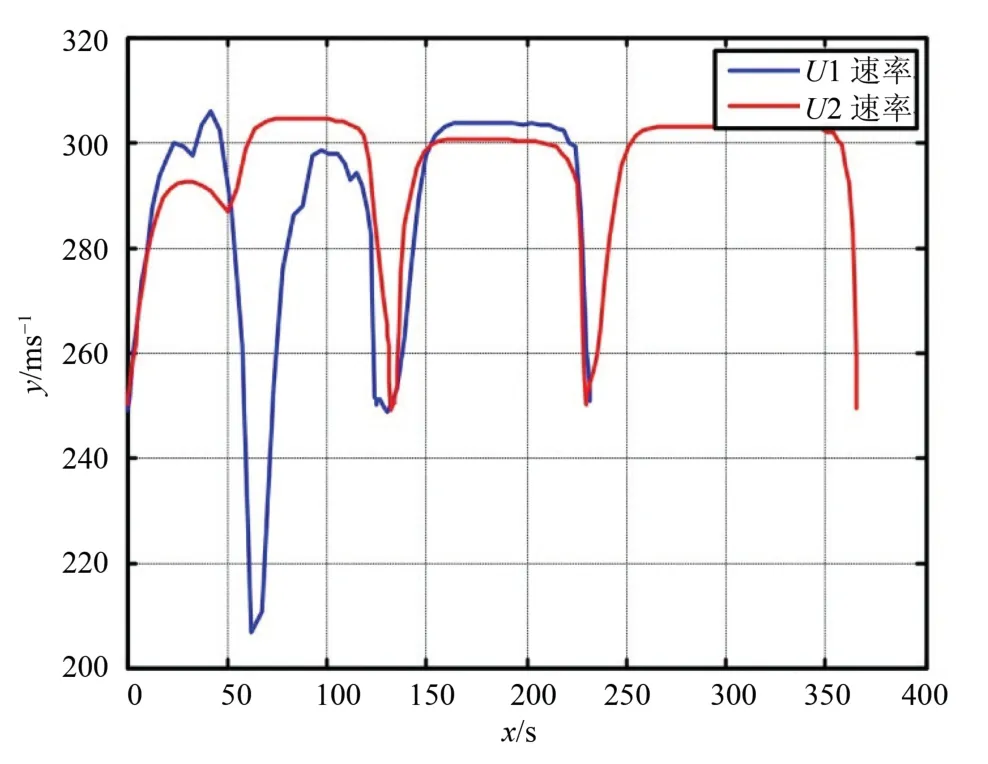
图4 无人机速率随时间变化曲线

4 结论

采用分层优化的机制解决多无人机多任务航迹规划问题.提出了结合Dubins 曲线和B 样条曲线的方法规划考虑无人机平台性能约束的飞行航线.该方法能够获得对任务执行消耗的可信估计且计算高效,因此能够有效提高分层优化方法的效率.提出应用航线规划结果作为基于高斯伪谱法航迹规划的初始解,提高了航迹规划的计算效率.该方法可用于解决多机器人任务规划问题.