基于修正立方定律对单裂隙辐射流剪切耦合的研究

杨金宝， 柴军瑞， 许增光， 覃 源

(西安理工大学 省部共建西北旱区生态水利国家重点实验室， 陕西 西安 710048)

1 研究背景

关于裂隙渗流耦合特性的研究在工程中具有非常重要的应用，如地下工程开挖[1]，填埋处理[2]和能源开采[3]等。然而自然岩体中存在着无数条裂隙通道，各裂隙更是具有不同的几何特征和连通性。要了解岩体中裂隙水的耦合特性，首先要对单裂隙进行研究，而以整个岩体为单位进行研究是极其复杂的。因此，研究单裂隙的机械行为和水力特性是认知岩石裂隙渗流机制的重要基础。全面了解单裂隙在法向变形和剪切破坏的渗流耦合行为，在岩土工程和水利工程中至关重要。

自然裂隙中的稳态和不可压缩流动行为可通过Navier-Stoke公式来描述。但由于自然裂隙几何特征的影响，惯性项的存在使Navier-Stoke公式不能有效得出结果[4]。要简化公式计算，只有将裂隙简化为上下两个光滑的平行板组合[5]。Navier-Stoke公式被化简后得出的立方定律广泛地运用在单裂隙的渗流实验中，用来评估水力特性。立方定律描述了渗流量与裂隙孔径立方之间的关系。然而已有实验表明立方定律倾向于高估天然岩石裂隙的渗透性[6]，并且这种偏差将随着裂隙几何特征复杂性的增加而增加[7]。许多学者采用等效裂隙宽度[8]、考虑粗糙性[9]、分析曲折效应[10]和引入裂隙面面积接触率[11]对立方定律进行修正使其符合工程实际。而对于平行板辐射流，已有的辐射流立方定律对裂隙的渗流能力也同样存在高估的现象。该研究进行了平行板辐射流实验，发现使用现有公式计算的流速通常大于实验数据。而且，当隙宽增加时，这种偏差将变得更加明显，这将降低立方定律的适用性。

裂隙的水力行为受裂隙面几何特征[12]和隙宽[13]的影响显著。几何特征的差异性会影响渗流流线的变化，隙宽的大小会使渗透性产生变化。法向压力[14]主要影响裂隙的隙宽大小，而剪切[15]会产生更复杂的耦合关系。Javadi等[4]初步研究了剪切作用对裂隙水的非线性作用，表明临界雷诺数主要取决于裂隙的几何形状。剪切的发生会使原本相对匹配的裂隙产生错位，上下裂隙面的孔径产生改变，对水流产生扰动。剪切过程通常会伴随着剪切破坏的发生，从而会改变上下裂隙面的几何特征。同时剪切破坏产生的碎块会随着剪切运动填堵在裂隙通道内，从而影响孔径大小并改变流体的流动路径，这对裂隙水流动特性的影响更复杂。Nemoto等[16]通过数值模拟发现不同的剪切方向会引起渗透率的各向异性，而Matsuki[17]认为渗透率随着剪切位移而增大与剪切角度无关，且初始孔径的分布会增强沟槽流。而对于本实验研究的辐射流模型则不存在剪切方向与初始孔径分布差异性的问题，也就避免了剪切方向的影响。

大批学者研究了法向应力对裂隙流的影响，例如峰值强度、临界雷诺数、线性和非线性系数随法向应力的变化[13-14, 18]。Javadi等[19]和Rong等[5]研究剪切位移对流速、剪应力和法向位移的影响。目前研究剪切作用对裂隙水力特性[20]的文献还不是很多，大多集中在裂隙力学性质[21]上的研究。关于水力特性的文献主要集中于研究渗流通道的变化和渗透性的改变，而力学性质方面的文献则主要研究剪切应力和法向膨胀的变化。上述文献大多数都是单独研究剪切过程中水力特性和力学性质的变化，忽略了将力学性质和水力特性两者联系起来对比分析。并且在现有的文献中，绝大多数的剪切渗流耦合实验是在较低液压水头下进行的[5]，但是在水利工程中，水工建筑物所处的液压水头都非常高。分析裂隙在高液压水头下的水力特性是对工程施工安全的重要保障。因此在高液压水头下进行渗流耦合实验的研究十分有必要。

本文采用恒定法向应力和匀速剪切共同作用在裂隙试件上，并通入恒定高水头进行环形齿状裂隙辐射流耦合剪切实验。目的在于研究裂隙的力学性质和水力特性。该研究进行了平行板辐射流实验，利用Provost等[22]提出的裂隙模型对辐射流立方定律进行了修正。通过修正的辐射流立方定律对裂隙的水力特性进行了分析，将裂隙的力学性质与水力特性进行了对比分析，寻求两者之间的关联。

2 理论背景

2.1 立方定律

当流体中的惯性力对流体运动状态的影响较小时，Navier-Stokes公式可简化为线性Stokes公式，该公式也称为线性达西定律：

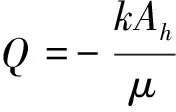
(1)

式中：Q为流量，m3/s;k为裂隙渗透率,m2;μ为动力黏度，Pa·s;Ah为裂隙横截面积,m2。

若将岩石裂隙简化为光滑平行板[5],基于达西定律的有效假设，立方定律可写成流量与孔径立方成线性比例的形式：

(2)

式中：w为垂直于流动方向裂隙的宽度,m；μ为动力黏度，Pa·s ；e为光滑平行板之间的距离,m；p为压力梯度，Pa/m;k=e2/12；Ah=w·e。

在光滑平行板模型得到稳定流的立方定律的基础上，给出了适用于辐射流的立方定律如下[23]：

(3)

CAO等[23]修正的立方定律如下：

(4)

式中：r为试件半径，m。

在本实验中，发现立方定律和Cao等[23]修正的立方定律仍然存在较大的误差。

2.2 渗流模型修正

考虑到辐射流的扩散特性，将采用Neuzil提出的裂隙流模型进行研究[19]，并对其模型推导出的公式进行改进，得到适用于辐射流的立方定律。Maini通过实验表明，水流在裂隙中流动倾向于在裂隙狭窄部分周围偏转，这会减小流动方向上孔径变化对水流的影响[24]。Iwai认为水流在孔径变化不大的裂隙中流动时，可以很好的用平行板流动近似[25]。

如图1(a)所示，将辐射流试件n等分(n趋于无穷大)，使得每一扇形的圆心角θ都无限小。再将扇形元件进行n等分，其圆心角为θi(如图1(b))。由于进行了无限细分，因此扇形的圆弧可以近似成直线段。如图1(b)的扇形模型可以简化成如图1(c)所示的平行板模型。将图1(c)中的裂隙模型分成n个区段，每个区段的宽度为l，裂隙孔径的总宽度为L。图1(c)模型考虑了垂直于水流方向上孔径的变化情况，在沿着水流方向上使用光滑平行板定理。

由于裂隙模型被n等分，所以每个区段上都适用光滑平行板定理。因此，当相邻段之间的孔径变化不大时，则可以忽略相邻段立壁的阻力效应。通过图1(c)中每个区段的流量可以由如下公式(5)计算得出：

(5)

式中：J为水力坡度;b为隙宽，m；γ为水的重度，N/m3。公式(5)被称为简单的Poiseuille公式，也称为“立方定律”，因此，图1(c)模型中裂隙的总流量可写为公式(6)：

(6)

公式(6)是n段流量的总和。 每一段的流量由公式(7)给出：

(7)

将图1(b)中扇形的弧长简化成直线段，即图1(c)中的平行板模型。由此就有平行板的宽度等于扇形的弧长，如公式(8):

(8)

因此，图1(c)中单个区段的流量可以写为式(9)：

(9)

将通过每个小扇形区域的流量累加得到整个模型的流量，可由式(10)给出：

(10)

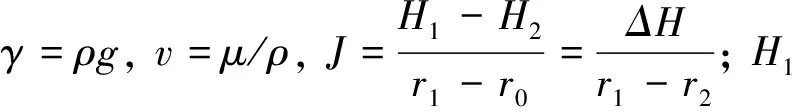
(11)

由公式(11)得到水力隙宽e为：

(12)

辐射流的单宽流量公式为：

(13)

2.3 非线性流

高液压水头下，惯性效应会越来越明显，这就会引起非线性流动偏差。对于强惯性效应引起的非线性流动偏差，Forchheimer引入了一个二次项[5]：

(14)

(15)

式中：β为非达西流系数或Forchheimer系数，其维数为[L-1];A为与流体性质相关的线性系数;B为与介质几何形状有关的非线性系数。当惯性效应变可以忽略不计时，则β=0，此时Forchheimer定律可以简化为公式(1)所示的达西定律。

雷诺数的大小反映惯性效应的影响程度：

(16)

使用Q=Ahv=wev和U=μ/ρ来化简公式(16)，这样就产生了一个不需借助e求解Re的表达式。同时也就避免了在测量裂隙孔径和流速产生误差，影响Re值的精确性。

关键雷诺数表征流动从线性向非线性的转变，定义为非线性压降占总压降的百分比。由Forchheimer定律可知，非线性压降占整体压降的百分比为：

(17)

将公式(17)代入公式(16)简化可得：

(18)

将公式(15)代入公式(18)，并用k=e2/12和Ah=ew进行化简得出一个更简洁的Rec表达式：

(19)

在不同的工程应用实践中，一般α取10%[4]，Rec表达式可化简为：

(20)

图1 辐射流细分化模型、扇形细分化模型和扇形等效直板流模型

3 研究方法

3.1 实验设备

本研究采用TJXW-600仪器进行辐射流剪切耦合实验，装配裂隙试件的剪切盒示意图如图2所示。该实验仪器主要由荷载加载系统、水头增压系统和数据采集系统组成。荷载加载系统由法向和剪切加载控制共同作用，通过伺服油源提供荷载，由传感器控制荷载大小。

水头增压系统由集水装置和氮气装置组成，水头的大小调节由氮气装置稳定调节。数据采集系统由力传感器、位移传感器和高精度电子秤组成，采集到的数据均保存在微机中。该仪器可以在恒定法向应力(CNL)下进行剪切渗流实验，并且可以实时准确的测出实验过程中数值的变化。

3.2 试件制备

由于石膏的低渗透性，假设水只在裂隙中流动。因此采用α型高强度石膏浇筑裂隙试件，裂隙分为上下两个试件(如图3(a)、3(b)所示)。采用石膏与水的配合比为4∶ 1来配置半径为100 mm，高为75 mm的裂隙试件。待试件自然干燥一周后，用全氟防护剂均匀涂刷试件形成憎水膜层，以减小实验过程中试件吸水对测量流量和试件强度的影响。试件采用中心注水辐射流的形式，注水孔半径为4 mm。试件的物理力学参数如表1所示。

图2 TJXW-600实验装剪切盒示意图

图3 下试件、上试件、下试件破坏面、上试件破坏面、下试件清理后破坏面和上试件清理后破坏面

3.3 实验步骤

用图2所示仪器进行辐射流剪切耦合实验，分析法向应力和剪切位移速率对渗流特性的影响。在对辐射流立方定律修正的实验中，以平行板试件在0.6 MPa的水头下进行渗流试验。在研究剪切速率的影响时，施加0.6 MPa的恒定水头和60 kN的法向荷载，分别以5、10、15、20、25 mm/min的剪切速度进行实验。在研究法向荷载的影响时，在0.6 MPa的恒定水头和15 mm/min的剪切速率下，以40、50、60、70、80 kN的法向荷载进行实验。来自法向和剪切传感器以及电子秤测量的数据(每0.1 s记录一次)将会通过数据处理系统保存在计算机里。

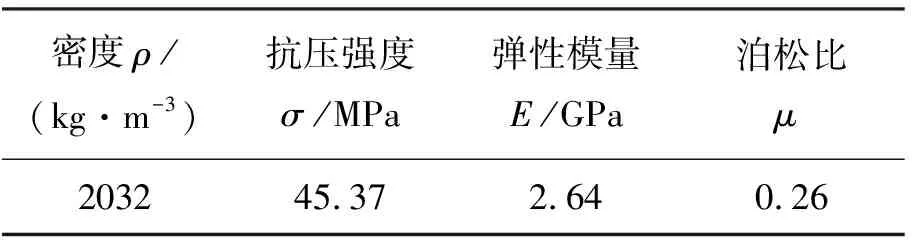
表1 试件的物理力学参数

4 结果和讨论

4.1 公式比较

为了验证立方定理的适用性，将不同大小的裂隙宽度代入公式(3)、(4)和(11)计算相应的流量进行比较，结果如图4所示。从图4可以看出，公式(11)相比于公式(3)和(4)更贴合于实验数据。当裂隙宽度小于0.1mm时，公式(3)和(4)能很好地贴合实验数据。然而随着裂隙宽度增加，计算流量与实验值之间的偏差变大。从图4可以看出，使用公式(3)和(4)分别在0.3和0.4 mm隙宽时的计算流量大于在0.6 mm隙宽时的实验流量。因此，当裂隙宽度较大时，公式(3)和(4)在实际工程中的应用将受到限制。对于公式(11)给出的立方定律，计算出的流量和实验值吻合得很好。即使当隙宽增加时，由公式(11)计算的流量与实验值之间的偏差也不会急剧增加，偏差值趋于稳定。并且随着裂隙宽度增加，渗流能力也增强，此时偏差值与渗流量的比值逐渐减小。立方定律的准确性可以用修正系数公式(21)表示：

(21)

式中：qequ为公式计算值；qexp为实验实测值。c越小，立方定律越接近实验实测值。如图4(b)所示，c的值随着裂隙宽度的增加而减小。此外，发现使用修正立方定律的c值变化较小，并且小于使用公式(4)计算c值的50%。因此，将公式(11)应用于实际工程中的渗流计算，其结果更准确。

修正后的立方定律仍然会高估裂隙的实际过流能力。 这是因为在修正立方定律的过程中忽略了两个问题：(1)是在不考虑粗糙度的简化裂隙模型下，修正的立方定律，而实际裂隙不同于理想化的平行板， 粗糙度的存在会使裂隙的渗流能力大大降低。(2)渗流存在惯性效应，而立方定律中却没有涉及。这都会导致修正的立方定律夸大裂隙渗流能力。

随着裂隙宽度的增加，c值减小，这是因为流体与裂隙壁之间存在相对运动，此时粗糙的裂隙会急剧扰乱近裂隙面的流线，消耗流层的动能。并且靠近裂隙面的流动层将制约距裂隙面较远的流层，减小了流动层的动能，从而降低裂隙的渗流能力。在相对较宽的裂隙中，中间流层相对远离裂隙面并且受黏性力的影响较小，整体流速降低较少。因此，在相同的液压水头下，隙宽较大裂隙的渗透能力比小隙宽裂隙的强。立方定律不考虑黏滞力对裂隙渗流能力的影响。随着裂隙宽度逐渐减小，裂隙水的雷诺数增加，裂隙的渗透性降低。随着隙宽的增加，裂隙粗糙度对流体的速度和流态的影响区域占比降低。流体流动的影响将逐渐减小，裂隙的渗流能力将增加，这将有助于降低偏差。因此，随着隙宽增加，实测数据与修正立方定律的计算值之差的比值也减小。因此，即使在较大隙宽时，修正的立方定律仍然具有有效性。

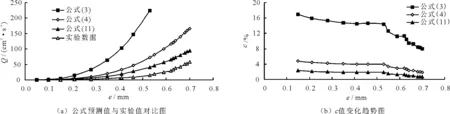
图4 公式预测值与实验值对比图和c值的变化趋势图

4.2 裂隙试件的力学性能

图5显示了在恒定法向应力下的剪切力学特性。从图5(a)中可以看出剪切呈现不稳定的破坏特性。剪切位移在0～0.75mm时，裂隙面会发生沉降并互锁，这个过程中裂隙面基本没有损伤，而刚度和接触面积都会增加。当剪切位移为4～5 mm时，裂隙开始发生剪胀效应，法向位移急剧增加。当增加到最大值时，因为裂隙中齿状凸体具有一定的宽度，会有一段大约2 mm的相对平稳期。当发生剪切破坏时，两个剪断的凸体在接触过程中法向位移保持平稳。当两个凸体错开后，凸体与凹槽形成第二次轻微的互锁。由于剪切破坏产生的碎块会填堵凹槽，所以第二次互锁效果很弱，法向位移减小。随着剪切位移增大到6～8 mm时，将会产生轻微的破坏，这体现在图5(b)中剪应力在骤降后会有一段起伏期。剪切位移达到12 mm之后，法向位移趋于恒定值。上、下试件受剪切破坏后的裂隙面形式如图3(c)和3(d)所示，清理剪切破坏碎屑后的裂隙面如图3(e)和3(f)所示。

如图5(b)所示，剪应力阶段性变化明显。在未发生剪切破坏前，剪应力会急剧攀升。当剪切位移达到4～5 mm时，剪应力达到峰值。在此后的2 mm内，剪应力骤降大约1 MPa。经过剪应力的骤降后，在之后的5 mm剪切位移内，剪应力减小的速率会变的缓慢。在剪切位移到12 mm后，剪应力基本稳定。从图5(b)中可以看出，不同的剪切速度对应的峰值剪应力是不同的。峰值剪应力和最大法向位移与剪切速率的关系如图6所示。从图6中可以看出，峰值剪应力与剪切速率呈驼峰状，随着剪切速率的增加先递增，达到阈值后降低。而对于残余剪应力，不同剪切速率的渗流耦合实验大约均在剪切位移达到12 mm后变为恒定值。可以看出剪切破坏的程度不同其对应的最终恒定值也会有所不同，没有一定的规律。对于不同的剪切速度，峰值剪切强度也不同，且随剪切速度的增大会先增大后减小。而对于残余剪切强度，则不受剪切速度的影响。

从图5可以看出剪应力与法向位移的变化具有良好的一致性。剪应力和法向位移随剪切位移的增加，都会先急速增大，达到最大值后会有一小段骤降，随后缓慢减小达到稳定值。且剪应力与法向位移达到最大值时的剪切位移也几乎一致。图7为裂隙面剪切破坏示意图。从图7(a)和7(b)的对比中可以看出，法向位移小的试件拥有更大的抗剪断宽度，其抗剪强度越高。因此裂隙的抗剪强度和法向位移是存在关联的。

从图6中可以看出峰值剪切强度与剪切速度之间并非简单的单调关系，存在临界剪切速率。当小于临界剪切速率时，抗剪强度与剪切速率构成的曲线斜率大于0。当大于剪切临界速率时，抗剪强度与剪切速率构成的曲线斜率小于0。与此同时，随着剪切速率的增大，裂隙的最大法向位移呈现先减小后增大的变化规律。由图7可知，当法向位移大时，裂隙之间咬合地更紧密，抗剪断能力就越强，因此抗剪强度也随之增大。由此，可以看出最大法向位移与峰值剪切应力具有同步性。峰值剪切应力与残余剪切应力的差值也符合随着剪切速率的增加先增大后减小的趋势。

4.3 裂隙水的水力特性

图8为在不同的法向压力和剪切速率时，系数A在剪切过程中的变化。如图8(a)所示，在恒定水头和剪切速率下，以不同的法向压力进行剪切渗流试验，系数A在剪切过程中经历了先增大后减小,最终趋于恒定值的过程。在0～5 mm的剪切位移中，系数A经历了从1.010×1010到1.958×1010的最大增长，增幅达93.86%。同时也经历了从1.383×1010至1.963×1010的最小增长，增幅为41.94%。在发生剪切破坏前，最小和最大法向压力下的系数A的涨幅比为2.24倍。当剪应力达到峰值时发生剪切破坏，系数A在5～7 mm内会发生陡降。此陡降是因为发生剪切破坏导致裂隙数量和隙宽急剧增大，渗流通道增多增大造成的。在7～12 mm内，系数A下降的速率会逐渐减缓。因为在发生剪切破坏后，剪切破坏产生的碎块和碎屑随着剪切移动和碾压。运动到沟槽处时，碎块和碎屑会将沟槽填埋，使渗流通道趋于平缓并减少流动路径。在12～20 mm内，系数A趋于稳定。最终系数A的减幅为42.37%～65.45%，变化幅度比剪切破坏前小。

在剪切破坏发生前，系数A与剪切位移的增长呈线性关系。并且不同法向压力下的线性系数近似一致。因此在发生剪切破坏前，系数A的变化速率与法向压力无关。而系数A的初始值与法向应力有关，法向应力越大，系数A越大。达到剪切峰值时，各法向力作用下的系数A也接近一致。只是试件所受法向应力较大时会较早达到最大值。当发生剪切破坏后，系数A先急速下降，后缓慢下降至恒定值。系数A下降速率与所受法向应力成反比，即较小法向应力作用时的下降速率较快，然而都在剪切位移为17 mm时达到恒定值。当系数A趋于平稳时，可以看出终值与法向压力成正比例关系。

不同剪切速率对系数A的影响如图8(b)所示。由图5(b)可知不同剪切速率会在不同的剪切位移处产生峰值剪应力。因此剪切破坏前系数A的变化速率也将不一致，但会产生几近一致的系数A。当发生剪切破坏后，系数A在不同剪切速率的情况下有着接近一致的下降趋势，直到趋于稳定时会产生些小差异。稳定值与剪切速率呈反比例，较大的剪切速率拥有较小的稳定值。这是因为剪切速率大时，相应裂隙面接触的形式变换也将更快速复杂。流动路径将变得更加曲折，主要通道变少且起伏变大，从而渗透率变得各向异性[16]。裂隙流变得不平稳，线性系数降低。

图9给出了法向压力和剪切速率对系数B的影响规律。对比图8可以看出，在不同的法向应力和剪切速率作用下，系数B有着与系数A基本一致的变化规律。系数B变化幅度更大。非线性系数B从剪切开始到剪切破坏增加101.58%～276.02%，发生剪切破坏后减小66.79%～88.06%的减小。

在剪切破坏实验中，临界雷诺数Rec在不同法向压力和剪切速率情况下随剪切位移的变化情况如图10所示。从图10中可以看出在剪切破坏发生前，临界雷诺数逐渐减小。达到峰值剪应力时，临界雷诺数降到最低值。当剪切破坏发生时，临界雷诺数会增大，且增加的速率逐渐降缓，最后趋于稳定值。然而在不同法向压力作用下，临界雷诺数的变化存在较大的差异性。在图10(a)中可以看出，施加较大法向荷载的渗流临界雷诺数更小。在剪切破坏前，临界雷诺数在施加法向荷载较小时，时具有更大的下降速率。达到峰值剪应力时，不同法向应力作用下的试件都达到了几乎一致的最小临界雷诺数。且减幅占初始值比例较大，为29.57%～48.43%。随着剪切破坏的发生，临界雷诺数开始增加并超过初始临界雷诺数。增幅达到73.53%～189.41%。随着法向压力的增加，临界雷诺数的稳定值也逐步减小，最小稳定值与最大稳定值相差4.441。本试验得的系数A、B与Zhou Jiaqing等[18]、Rong Guan等[5]和Javadi等[4]的研究成果有着相同的变化趋势，但是变化的量级要比之前报告中的小，并且变化幅度更趋于平滑。

从图10可以看出不论边界条件如何，发生剪切破坏后的裂隙拥有更大的雷诺数。这表明剪切破坏后的裂隙对水流的惯性损失将减小。因为裂隙剪切破坏产生的碎块在法向和剪切荷载共同作用下，填埋在凹槽中，如图3(c)和3(d)。正因为裂隙面变的平滑且流动路径也变的平直，裂隙水的动能损失减小，惯性势能也比初始裂隙时的大。这也体现在图9中，非线性系数项在剪切后的稳定值小于剪切前初始值。因此剪切破坏后的裂隙流态更平稳，从而增加了裂隙的渗透性。

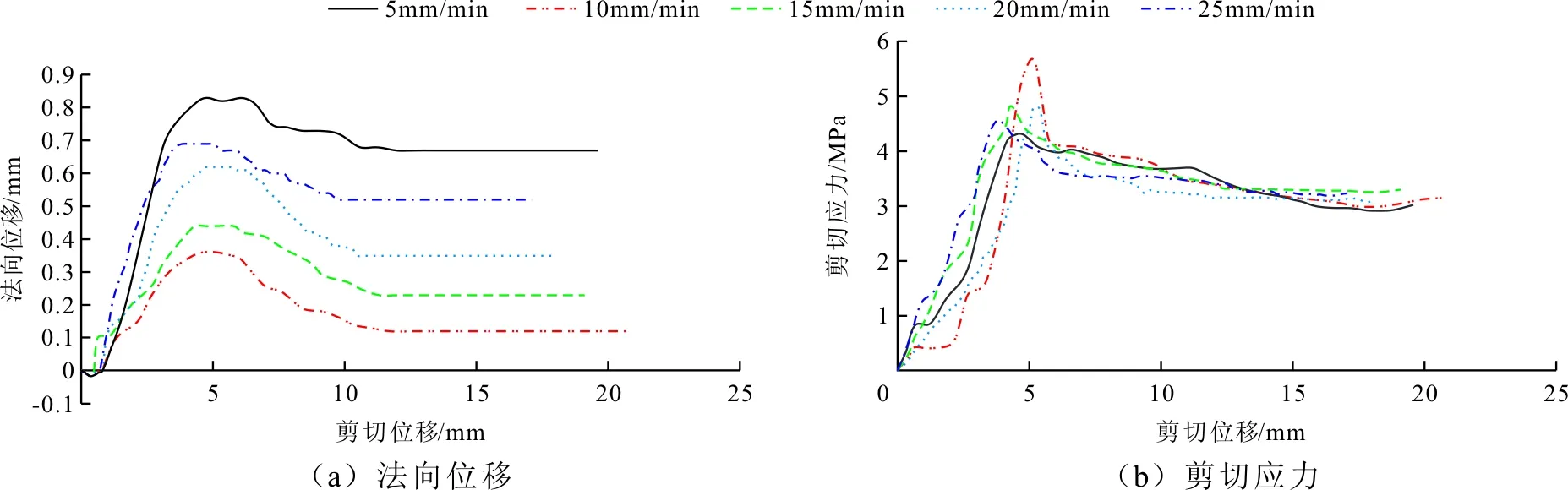
图5 法向位移和剪切应力受剪切速度影响规律

4.4 裂隙力学性质与水力特性的关系

对比上述图中的力学性质和水力特性表明，可以发现它们之间并不是相互独立的存在，并且随着剪切位移经历了3个不同的阶段。

第1个阶段：当裂隙达到最大法向位移时，此时剪应力达到峰值，而此时裂隙水的流动型态会变的更复杂。系数A、B都会随之增大，渗流变的更加非线性。临界雷诺数也变的更低。这说明渗流在较低的雷诺数时流态就会从线性过度到非线性状态。

第2个阶段：随着剪切的继续进行，法向位移、剪应力和系数A、B首先发生骤降随后缓慢减小。可以看出在剪切破坏后，流态变的良好。临界雷诺数增加的速率则会逐渐减小。剪切破坏之后裂隙产生更多的流动通道，使渗流流态变的更好。

第3个阶段：裂隙法向位移趋于稳定值时，剪应力也将达到恒定值。裂隙更加平顺，流动通道更加集中，渗流流态将变得平顺。此时的系数A、B缓慢减小趋于稳定，临界雷诺数增加至稳定值。

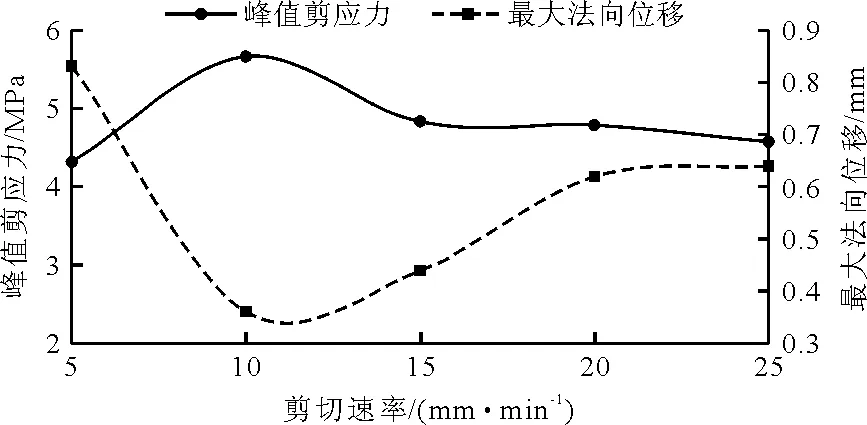
图6 峰值剪应力和最大法向位移与剪切速率的关系

因此通过裂隙辐射流剪切耦合试验可以得出，力学性质与水力特性之间存在关联。从力学性质变化可以预测出水力特性的变化情况。本文只是粗略地探讨了剪切破坏时力学性质与水力特性之间变化的关联，两者之间存在某种可以定量之间的关系。希望在以后的工作中能继续深入研究，可以根据裂隙的力学性质的变化定量的预测出一些水力特性的大小变化。

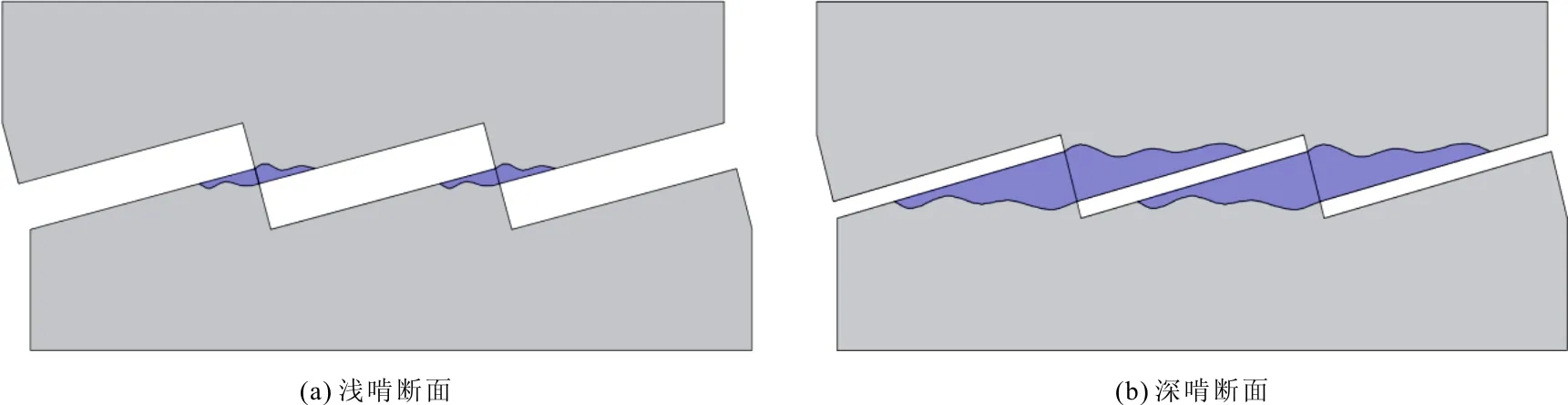
图7 裂隙面剪切破坏示意图(深色部分为破坏区域)

图8 恒定水头下系数A随不同法向压力和剪切速率随剪切位移的变化曲线

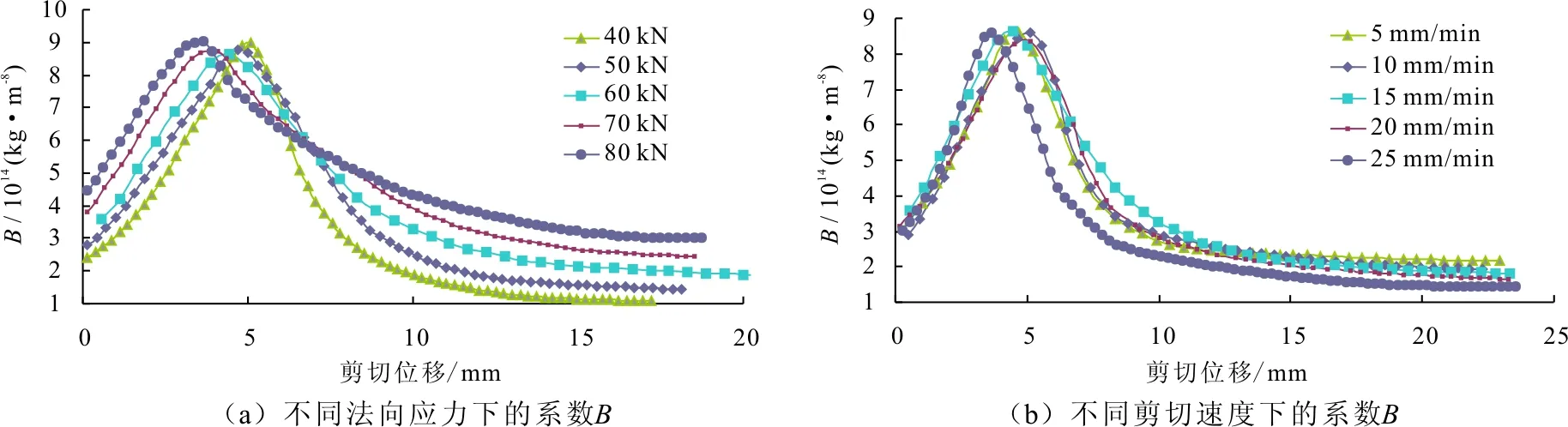
图9 恒定水头下系数B在不同法向压力和剪切速率随剪切位移的变化曲线

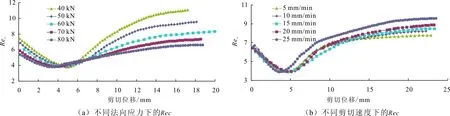
图10 恒定水头下临界雷诺数在不同法向压力和剪切速率随剪切位移的变化曲线

5 结 论

本文对辐射流立方定律进行修正，并通过实验对裂隙流在剪切破坏中的力学性质和水力特性进行了研究。通过裂隙流模型推导出立方定律的新公式，将新辐射流立方定律运用到剪切渗流耦合研究中，讨论了剪切过程中的力学性质和水力特性的变化。主要研究结果如下：

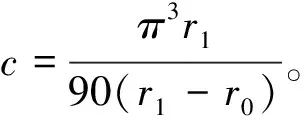
(2)剪切过程中裂隙存在剪胀现象，并且剪胀的范围与试件齿形凸体的底宽相同(10 mm)。剪应力的变化与裂隙的法向位移同步，峰值剪切强度与剪切速率之间并非单调关系。而是随剪切速率的增大，剪切强度会有先增大后减小的趋势。

(3)Forchheimer定律中的系数A和B在不同法向压力和剪切速率下随剪切位移的变化明显，且都具有先增大后减小的变化趋势，但系数B的变化幅度要比系数A大。系数A先经历了41.98%到93.91%的增大，随后经历了42.37%到65.45%的减小。系数B经历了101.58%到276.02%的增大，随后经历了66.79%到88.06%的减小。B与A的比值随着剪切位移先经历了41.98%到93.91%的增加，随着剪切破坏的发生最终小于初始比值。

(4)临界雷诺数在不同法向压力和剪切速率下随剪切破坏的发生会先减小后增大，并且剪切破坏后的临界雷诺数大于初始临界雷诺数。这表明经剪切后的裂隙拥有更小的粗糙度，流动通道变得平顺，渗流流态变好。

(5)在剪切过程中，裂隙的力学性质和水力特性之间存在关联。水力特性会随着力学性质的变化发生同步变化，而且具有相似的趋势。

裂隙的力学性质和水力特性与裂隙的形式和尺寸有关。由于实验条件限制了对更多不同的裂隙进行实验。通过更多形式的裂隙实验来定量的寻求水力特性与力学性质之间的关系和修正立方定律，这将是以后研究中重点研究的内容。