HYPE模型在成屏一级水库的适用性研究

熊丁晖， 桂发二， 张洪宾， 周 泉， 罗 源， 李韩文， 陈 华

(浙江贵仁信息科技股份有限公司， 浙江 杭州 310051)

1 研究背景

成屏一级水库位于浙江省丽水市遂昌县瓯江支流松荫溪上游，距遂昌县城12 km，是松荫溪梯级开发的首级电站。坝址以上集水面积为185 km2，主流长为28 km。库区多年平均降雨量1 670 mm，多年平均流量5.84 m3/s。库区雨量时空分布不均，在多雨季节，尤其在7-8月份极易造成洪涝灾害，而在相对干旱的1-2月却常处于缺水状态。由于库区受局地气候影响较大，水文气象要素不稳定，小范围内地形起伏大，在降雨集中情况下易出现突发状况。因此，研究成屏一级水库入库流量的快速、准确预报有着重要的工程应用价值。

水文模型是水库入库流量模拟的重要工具之一，国内外已广泛应用水文模型进行水库入库流量研究。李艺婷等[1]将新安江模型的蓄满产流模式应用于浙江省台州市山区型和平原型两个水库的入库径流量模拟之中，取得较好的效果。魏恒志等[2]采用流溪河模型开展了白龟山水库入库洪水预报研究，结果表明流溪河模型具有良好的水文模拟性能。Anghileri等[3]将VIC模型应用于加利福尼亚奥罗维尔水库，模拟效果较好。然而，国内关于HYPE模型[4]在水库入库流量模拟方面的研究较少。本文以成屏一级水库为研究对象，应用HYPE模型推算长序列日尺度水库入库流量信息，探讨HYPE模型在成屏一级水库的适用性。

此外，国内外现有研究表明，虽然应用水文模型模拟流域日尺度流量过程总体效果良好，但是在洪峰模拟上略有不足，主要体现在模拟值较大幅度地低于或高于洪峰。金君良等[5]建立VIC模型模拟嘉陵江流域日径流过程，结果表明日径流过程的Nash效率系数在0.7以上，但几场暴雨过程对应的洪峰较高于模拟值。杨柳等[6]应用SWAT模型模拟山美水库集水区流域日尺度的径流过程，其日径流过程的Nash效率系数在0.8以上，但是依然有若干洪峰高于实测值。Golmohammadi等[7]同时评估了MIKE-SHE模型、APEX模型和SWAT模型在格兰德流域日尺度径流模拟的效果，结果表明3个模型总体效果较好，但是洪峰流量大于或小于模拟值。以上研究表明，水文模型在长序列日尺度径流模拟存在洪峰模拟不准确的问题，本文提出一种方法拟尝试解决这个问题。

2 资料和方法

2.1 研究区域

成屏一级水库坝址以上流域地形特征和雨量站分布见图1，土地利用和土壤类型见图2。雨量站有桂洋站、石柱站、垵口站、大公坑站和成屏一级站，流域出口位于成屏一级站。土地利用类型包括农田、森林、草地、水体、城镇等，其中森林面积占94%。土壤类型包括黏土、壤土和砂壤土，其中壤土由于组成比例不同分为壤土1和壤土2，砂壤土也由于组成比例不同分为砂壤土1和砂壤土2。

2.2 基本数据

使用HYPE模型模拟成屏一级水库入库流量需要的数据包括数字高程图、土地利用图、土壤类型图、气象数据、实测入库流量数据等。

(1)数字高程图。从SRTM数据库(http://srtm.csi.cgiar.org/)下载分辨率为90 m×90 m的数字高程图。

(2)土地利用图。从USGS数据库(https://www.usgs.gov/)下载分辨率为1 km×1 km 的2010年土地利用图。

(3)土壤类型图。从联合国粮农组织(FAO)和维也纳国际应用系统研究所(IIASA)所构建的世界土壤数据库HWSD (http://webarchive.iiasa.ac.at/Research/LUC/External-World-soil-database/HTML/index.html?sb=1)下载分辨率为1km×1km的土壤类型图。

(4)气象数据。从遂昌县气象局收集2013-2015年的降雨数据和温度数据。

(5)实测入库数据。从遂昌县气象局收集2013-2015年的成屏一级水库入库流量数据。

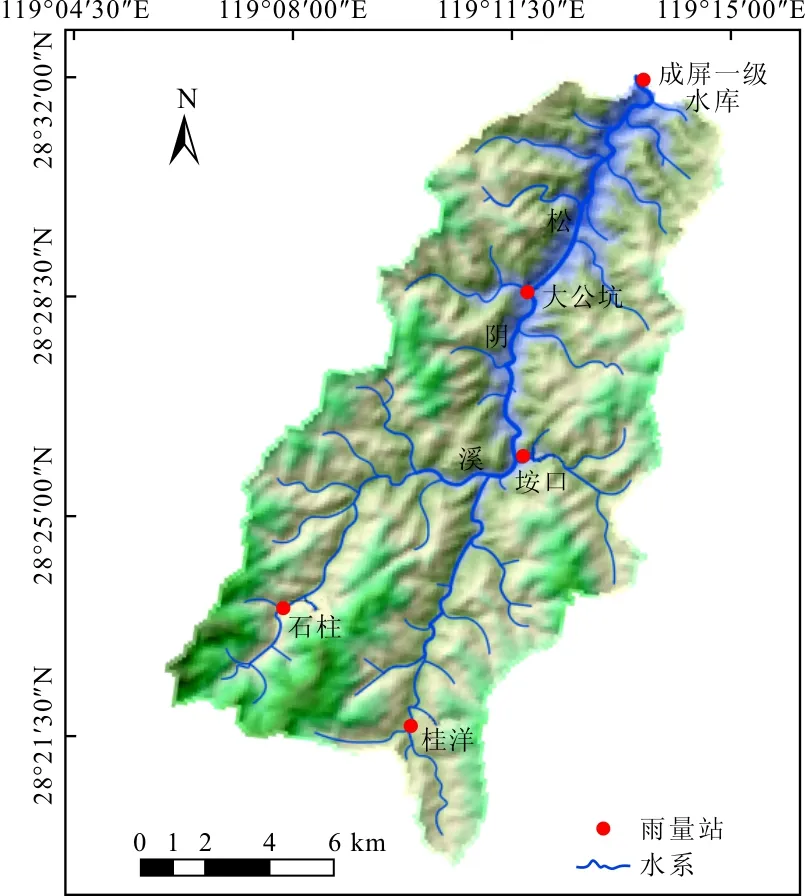
图1 成屏一级水库坝址以上流域地形特征和雨量站分布

2.3 方法

2.3.1 HYPE模型 HYPE(Hydrological Predictions for the Environment)模型是瑞典国家气象水文研究所在HBV模型的基础上研发的半分式水文模型，该模型综合考虑了多种影响流域径流的因素，将水文运动过程、氮磷输移转化过程和模型率定等结合起来，形成了一套完整的模型预报方案。该模型具有易于操作、结构清晰、参数率定速度快、模拟效果好等优点，被广泛应用于水量平衡研究、洪水设计、气候变化影响研究以及地下水模拟和水文预报等诸多方面[8-10]。

图3为HYPE模型的结构示意图。研究区域被划分为若干个子流域，每个子流域又被划分为不同的类，主要包括土地类、湖泊类和河流类，土地类由不同的土壤类型和土地利用类型组合而成。图4为HYPE模型的水文过程原理图。HYPE模型模拟的主要水文过程包括融雪和积雪、蒸散发、入渗、大孔隙流、渗流、地表径流、壤中流、排水管流和地下径流。除了模拟水文过程之外，HYPE模型还可以模拟径流及河流水体中营养物的浓度，如有机氮、无机氮、总氮、溶解态磷、颗粒态磷及总磷等。详细物理过程参考文献[4]。

2.3.2 LH-OAT方法 采用拉丁超立方-单次单因素(Latin hypercube-One factor At a Time，LH-OAT)方法进行HYPE模型参数敏感性分析[11]。LH-OAT方法将参数敏感度表示为一个无量纲的指数，反映模型输出结果随模型参数的微小改变而变化的敏感性程度[12]。

具体而言，假设模型有P个需要分析的参数，首先将这些参数的范围划分为N层，然后分别在每一层进行1次抽样，得到1个拉丁超立方抽样点(包括P个参数的集合)，总共进行N次抽样。之后对每个拉丁超立方抽样点中的参数进行一定程度的扰动，每次只改变1个参数，共有P次扰动。因此，N个拉丁超立方抽样点最终可产生N×(P+1)个参数组，将各参数的敏感度平均后即可得到其全局敏感度。该方法结合了拉丁超立方抽样算法的稳定性和单次单因素算法的精确性，大幅度降低了模型运行的次数和时间，提高了模型的计算效率。LH-OAT方法步骤如下：(1)在设定的P个参数范围内，采用拉丁超立方抽样并随机生成N个拉丁超立方抽样点；(2)采用单次单因素方法生成N×(P+1)个参数组；(3)针对生成的参数组，重复运行HYPE模型N×(P+1)次，输出变量为Nash-Sutcliffe系数；(4)计算各参数的全局敏感度，得到各参数最终的全局敏感度及排序结果。

全局敏感度计算方法如公式(1)。

(1)

式中：M为模型输出变量；N为抽样次数；γ为缩放因子；ε为扰动幅度；GSi为第i个参数的全局敏感度值。

2.3.3 DE算法 模型采用微分进化蒙特卡洛算法——DE算法[13](Differential Evolution Markov Chain method)进行参数率定。DE算法的基本思想是：对种群中的每一个个体，从当前种群中随机选择3个点，以其中1个点为基础，另外两个点作为参照作一次扰动，所得点与该个体交叉后进行“自然选择”，保留较优者，实现种群的进化。DE算法适用于无约束连续变量的全局优化问题，包括非线性规划、线性规划、非光滑优化等。

DE算法正是贝叶斯推理与微分进化两种算法的结合，它采用微分进化算法和马尔科夫链蒙特卡罗模拟对后验分布进行采样，获得参数的后验边缘概率密度函数，在此基础上获得参数的数学期望等统计量。

2.3.4 评价指标 本文采用4个指标[14]评价HYPE模型模拟效果，分别是决定系数(R2)、百分比偏差(percent bias，PBIAS)、纳什效率系数(Nash-Sutcliffe efficiency，NSE)、和均方根误差与标准差比值(ratio of root mean square error to standard deviation，RSR)，其公式如下：

(2)

(3)

(4)

(5)

3 结果与分析

3.1 模型构建

采用ArcGIS软件对成屏一级水库以上流域进行划分，网格大小为1 km×1 km，得到80个子流域和每个子流域的面积、平均海拔、河长以及子流域之间的流向，采用泰森多边形方法得到流域平均降雨量，80个子流域和泰森多边形见图5。根据土地利用图和土壤类型图得到14个类，这14个类的土地利用和土壤类型组成见表1，其中土壤共分成3层，第1层深30 cm，第2层深50 cm，第3层深20 cm。

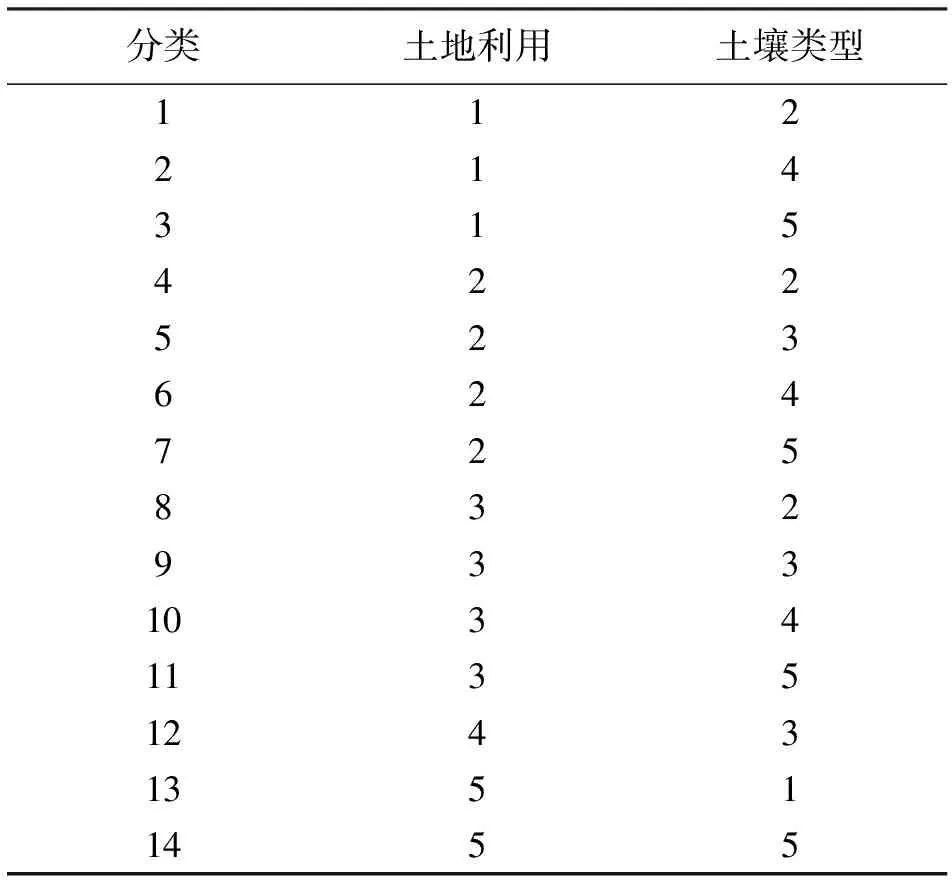
表1 成屏一级水库坝址以上流域14个类信息

注：土地利用中的1为农田；2为森林；3为草地；4为水体；5为城镇；土壤类型中的1为黏土；2为砂壤土1；3为壤土1；4为砂壤土2；5为壤土2。

图2 成屏一级水库坝址以上流域土地利用和土壤类型

3.2 参数敏感性分析

HYPE模型参数可分为4类：独立参数、与土地利用类型相关的参数、与土壤类型相关的参数以及和区域相关的参数。由于HYPE模型涉及到的参数众多，首先根据经验进行手动筛选，然后采用LH-OAT方法进行参数敏感性分析，最终确定的参数有17个，见表2。

图3 HYPE模型结构示意图

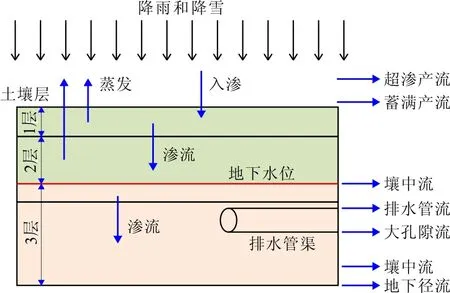
图4 HYPE模型水文过程原理图

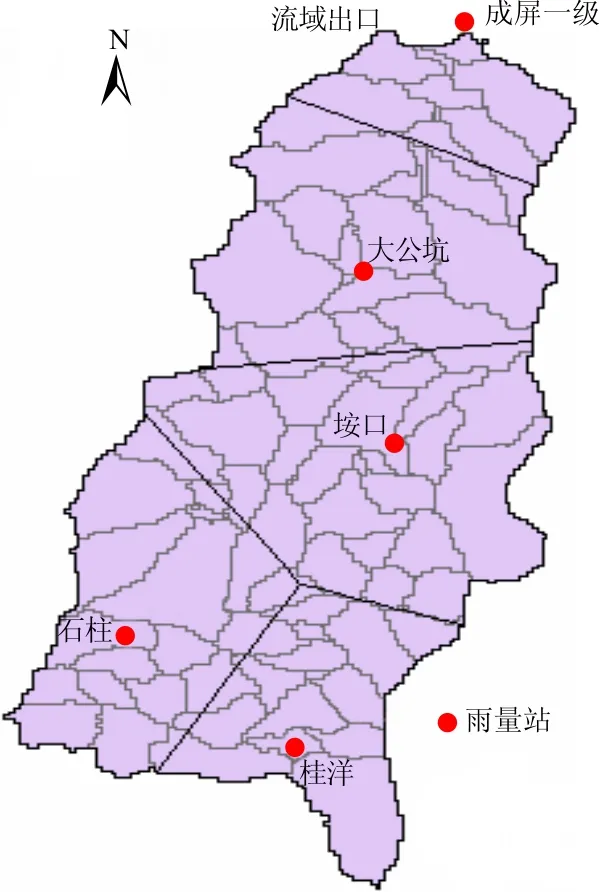
图5 成屏一级水库坝址以上流域80个

采用LH-OAT方法进行参数敏感性分析时，将HYPE模型的17个参数分成10层进行LH抽样，随机得到10个LH抽样点，将各个参数值除以相应参数的范围得到相对大小，结果见图6。

对抽样参数组进行OAT分析计算，计算次数为10×(17+1)=180次，使用目标函数NSE计算每个参数的全局敏感度，缩放因子γ取100；扰动幅度ε取0.01，结果见图7。从图7中可以看出，极敏感的参数为cevp，较敏感的参数为pcluse、cevpcorr、rrcscorr、rrcs1，一般敏感的参数为lp、preccorr、wcep、pcaddg，较不敏感的参数为cevpam、tcelevadd、rivvel、wcfc、epotdist、rrcs2、damp和mperc1。

表2 HYPE模型参数及范围

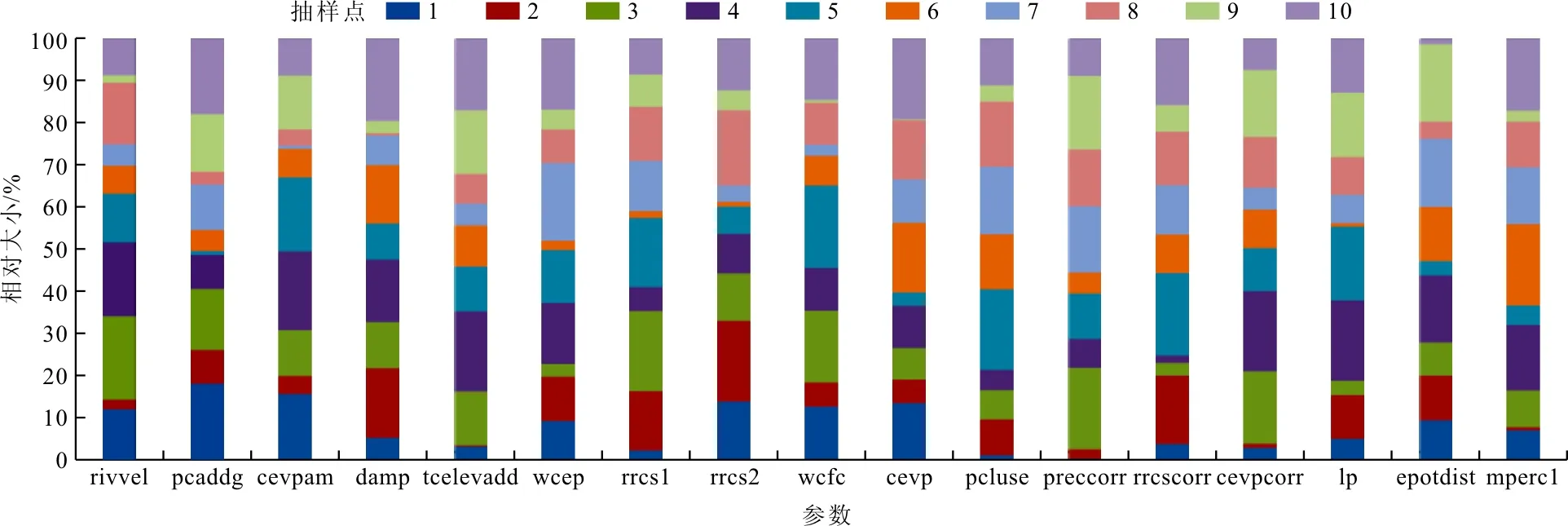
图6 LH抽样结果

图7 HYPE模型各参数全局敏感度

在确定HYPE模型各参数敏感度排序的情况下，采用DE算法进行参数率定。率定期选择2013年5月14日至2014年12月31日，参数率定结果见表3。

表3 HYPE模型各参数率定结果

注：S表示土壤类型，S1表示黏土；S2表示砂壤土1；S3表示壤土1；S4表示砂壤土2；S5表示壤土2。L表示土地利用，L1表示农田；L2表示森林；L3表示草地；L4表示水体；L5表示城镇。

3.3 模拟结果

采用HYPE模型对成屏一级水库入库流量进行模拟，率定期选择2013年5月14日至2014年12月31日，验证期选择2015年1月1日至2015年12月31日。率定期和验证期的HYPE模型模拟值和实测值对比分别见图8和9。

从图8中可以看出，率定期HYPE模型模拟值和实测值吻合程度较高，除了2014年8月20日的一场洪峰模拟值和实测值存在较大的差异，模拟值远低于实测值。从图9中可以看出，验证期HYPE模型模拟值和实测值基本吻合，同样2015年8月9日的一场洪峰，模拟值远低于实测值。此外，其他若干场洪峰模拟值也低于实测值。

为了进一步分析HYPE模型的模拟效果，采用4个评价指标进行评估，见表4。从表4中可以看出，率定期和验证期的NSE均大于0.8，R2均大于0.9，RSR均小于0.5，PBIAS的绝对值均在25%之间，表明不管是在率定期还是在验证期，HYPE模型对成屏一级水库日尺度入库流量模拟均达到要求，展现了HYPE模型较强的模拟能力。

表4 率定期和验证期HYPE模型模拟效果的4个评价指标

4 讨 论

4.1 误差分析

为了进一步分析HYPE模拟值与实测值之间的误差，将率定期和验证期的模拟值与实测值之差进行比较，见图10。结果表明在实测值较小时，模拟值和实测值之差在0附近，表明模拟值很接近实测值；在实测值较大时，模拟值与实测值之差偏离0较大，表明模拟值偏离实测值。上述结果表明HYPE模型能够较好地模拟实测值较小的情况，而在实测值较大的情况下模拟效果较差。图11为率定期和验证期模拟值与实测值之差随时间的波动图，同样反映了HYPE模型在洪峰模拟中的不足。究其原因，本文认为有两点：(1)输入数据的精确性有待商榷，尤其是降雨量数据。降雨量输入在很大程度上影响模拟结果，由于采用泰森多边形法对各个降雨站的雨量求平均，能否完全代替实际流域的雨量分布是存在疑问的[15]。此外，降雨量和实测径流量数据也可能存在一定程度的人为误差。(2)HYPE模型参数可能并不能反映出暴雨过程中的流域特征。由于在暴雨过程中，流域下垫面等情况发生了较大的改变，并且水流存在湍流等现象，导致暴雨过程中的流域特征和较小降雨情况下的流域特征存在明显差异。

HYPE模型参数是针对长序列进行率定的，其率定结果更反映较小降雨情况下的流域特征，而不能刻画暴雨情况下的流域特征，所以导致在洪峰过程中模拟值比实测值较小的现象。也许针对不同的降雨情况采用不同的参数进行刻画会更加符合现实情况。

4.2 新参数模拟

为了刻画暴雨情况下的流域特征，选择2014年8月1日-31日的一场洪峰进行率定，选择2015年8月1日-31日的一场洪峰进行验证，率定的参数见表5。其他时段的模拟值保持一致，考虑暴雨情况的率定期和验证期的模拟值和实测值对比图分别见12和13。结果表明2014年8月份和2015年8月份的洪峰模拟值更符合实测值。

考虑暴雨特征的率定期和验证期HYPE模型模拟效果的4个评价指标见表6。对比表4和6，率定期和验证期的NSE和R2变化不大，而表6的RSR和PBIAS明显小于表4，表明考虑暴雨特征之后的模拟值和实测值的偏差减小。

图8 率定期HYPE模型模拟值和实测值对比图

图9 验证期HYPE模型模拟值和实测值对比图

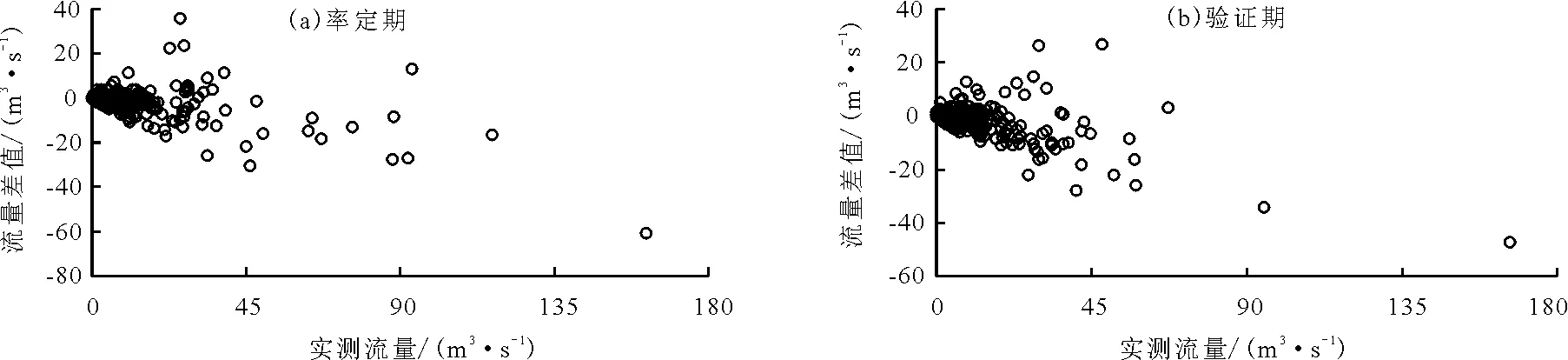
图10 率定期和验证期模拟值和实测值之差和实测值的比较(纵坐标表示模拟值和实测值之差)

图11 率定期和验证期模拟值与实测值之差随时间的波动(纵坐标表示模拟值和实测值之差)

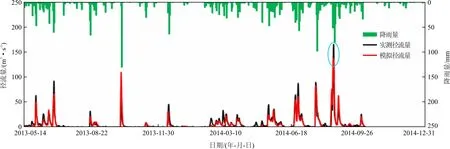
图12 考虑暴雨情况的率定期模拟值与实测值对比图

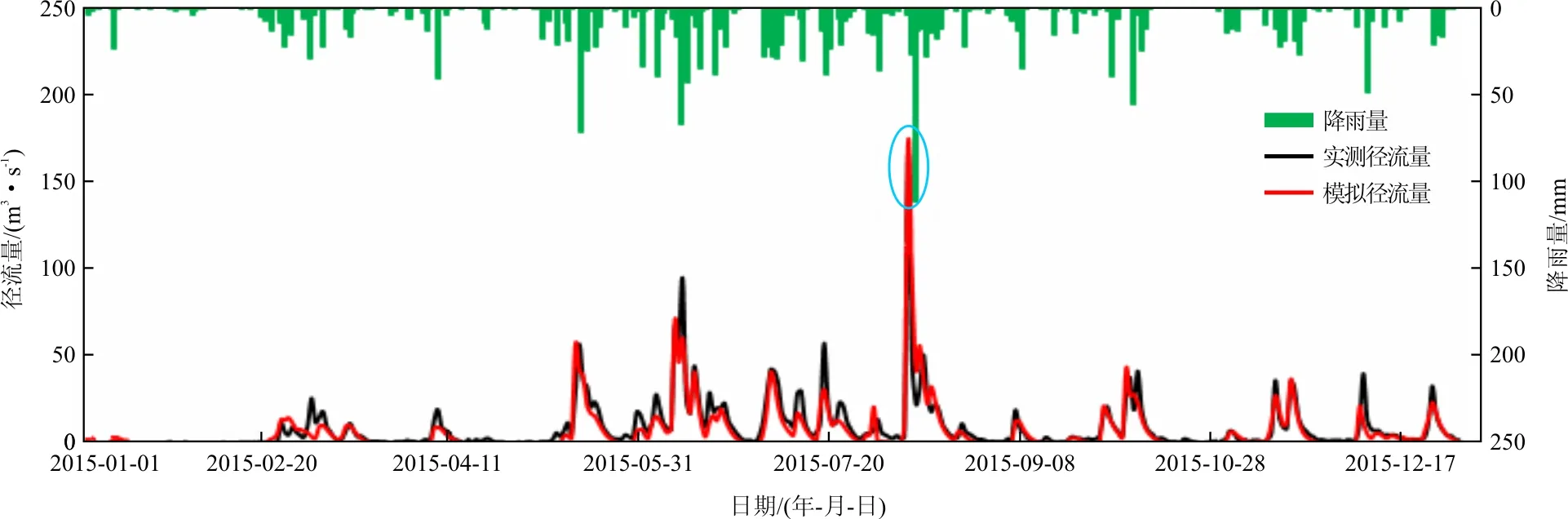
图13 考虑暴雨情况的验证期模拟值与实测值对比图

表5 考虑暴雨情况的HYPE模型各参数率定结果

注：S表示土壤类型，S1表示黏土；S2表示砂壤土1；S3表示壤土1；S4表示砂壤土2；S5表示壤土2。L表示土地利用，L1表示农田；L2表示森林；L3表示草地；L4表示水体；L5表示城镇。

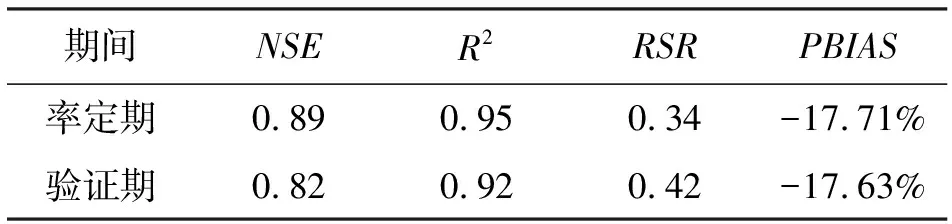
表6 考虑暴雨特征的率定期和验证期HYPE模型模拟效果的4个评价指标

5 结 论

结合LH-OAT方法、DE方法和HYPE模型，通过参数敏感性分析、参数率定和误差分析，对成屏一级水库入库流量模拟效果进行了较为全面的研究。得到如下结论：

(1)HYPE模型中极敏感的参数为cevp，较敏感的参数为pcluse、cevpcorr、rrcscorr、rrcs1，一般敏感的参数为lp、preccorr、wcep、pcaddg，较不敏感的参数为cevpam、tcelevadd、rivvel、wcfc、epotdist、rrcs2、damp和mperc1。

(2)HYPE模型率在率定期的纳什效率系数(NSE)为0.87，决定系数(R2)为0.94，和均方根误差与标准差比值(RSR)为0.42，百分比偏差(PBIAS)为-23.30%，在验证期的纳什效率系数(NSE)为0.83，决定系数(R2)为0.92，和均方根误差与标准差比值(RSR)为0.48，百分比偏差(PBIAS)为-20.88%。表明HYPE模型具备较强的模拟能力，能够用于长序列日尺度水文模拟。

(3)HYPE模型在洪峰模拟上模拟值低于实测值，原因可能是输入数据的精确性不足以及率定的模型参数并不能较好地反映出暴雨过程中的流域特征。

(4)对暴雨情况采用新的参数进行流域特征刻画，模型模拟效果更好。