辽宁省水资源优化配置研究
2019-03-26程瑞修
程瑞修
(辽宁省丹东水文局,辽宁 丹东 118000)
近年来,随着生态环境的变化和社会经济的发展,水环境污染、水资源紧缺以及水灾害频发等问题日趋严峻,水资源问题已成为影响人水和谐相处以及生态文明建设的主要因素。水资源管理是以水资源配置机制为依托实现人水和谐相处的理念,是一个涉及社会水与自然水共同管理的复杂系统,通过约束和协调用水主体及水工程最终达到水资源可持续利用的目标[1]。针对水资源优化配置模型的研究国内外许多学者开展了大量的研究和探讨,如王浩[2]等以黄河流域为例通过构建二元水循环系统耦合模型分析了该区域水资源配置模式,并给出了人工-天然二元水循环的结构模型。近年来,城市防洪排涝能力较低以及海绵城市的提出,不仅推动了雨洪管理模式的转变,而且有利于城市水资源的合理调控和配置,同时促进了定量评价水资源配置问题,如李卫华[3]等以塔里木河源区为例利用投影寻踪分类模型定量的评价分析了其水资源可持续利用水平。
目前,对水资源优化配置模型求解常用的方法主要有蚁群算法[4]、遗传算法[5]、粒子群算法[6]等,而萤火虫算法作为一种新的智能优化算法也被应用到水资源配置领域,并且涉及该方法的相关研究较少。据此,本文通过分析萤火虫算法建立了优化配置模型,以期为水资源的科学配置提供了一种新的思路和解决方法。
1 萤火虫算法
萤火虫算法首先是由YANG于2008年提出一种可用于萤火虫群体模拟和简化的智能算法,每个萤火虫在该算法中均可作为一个可行解,其亮度可代表此解的适应度[7]。萤火虫可根据其感知能力对更亮个体进行搜寻,通过迭代作用建立相应的邻域集,然后按照轮盘赌的方式移动,待移动完成后对其感知半径进行更新,并进入下一轮更新亮度的迭代。通过萤火虫的多次迭代逐渐聚集在较亮个体附近。对可变步长萤火虫算法采用连续函数优化法基本过程如下。
(2)利用公式(1)可建立比自身亮的萤火虫i的领域集Ni,萤火虫i采用轮盘赌的方式向领域集Ni中j萤火虫移动的概率pij,其表达式分别如下:

(1)
(2)
其中,萤火虫i至领域集Ni中j萤火虫的移动公式为:
(3)
式中,s—萤火虫移动步长,其他各参数同上。
考虑采用可变步长的迭代方式,以此获得更快的寻优搜寻速度,因此可采用下式对移动步长s进行调整:
(4)
式中,smax、smin—分别为移动步长的最大和最小值;gt、tmax—分别为当前和最大迭代次数。
(3)采用公式(5)、(6)分别作为萤火虫的更新感知半径与亮度,其表达式如下:
ri(t+1)= min{ri,max[0,ri(t)+β(ni-|Ni(t)|)]}
(5)
(6)

在当前解符合最优解或迭代至规定的次数时则停止迭代,否则重新代入进行计算。
2 建立水资源优化配置模型
2.1 目标函数
假定x为决策变量,采用下述模型作为辽宁省水资源优化配置方法,表达式如下:

(7)
式中,Z—水资源综合效益最大值;F(x)、G(x)—分别为水资源综合效益函数和条件约束集。
按照多个不同的子区将研究区域进行适当的划分,其中各子区均包含多个蓄水用户和供水水源,根据其供水范围又可将区域内的水源划分为独立水源和公共水源。将研究区域划分为K个子区,并且在k子区内存在J(k)个水用水部门和I(k)个独立水源,在此范围内存在M个公共水,可建立目标函数如下:
F(x)=opt[f1(x),f2(x),f3(x)]
(8)
式中,F(x)—水资源综合效益函数;f1(x)、f2(x)、f3(x)—分别为社会、经济、环境效益函数。
为便于优化模型的求解,可将式(8)中3个变量进行加权求和计算,公式如下:
(9)

采用区域内供水直接带来的最大经济效益代表经济效益函数f1(x),其表达式如下:
(10)

采用区域内最小的总缺水量来间接反映社会效益函数f2(x),其表达式如下:
(11)
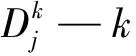
采用区域内最小的重要污染物排放量反映社会效益函数f3(x),不同区域污染物排放状况存在一定的差异,因此在选择重要污染物时应有所区别,通常选取较为常用的汞、石油类以及氨氮类等污染物作为参数指标,假定区域内共有N种污染物,则f3(x)表达式如下:
(12)

2.2 约束条件
结合已有文献对水资源配置模型的约束条件确定辽宁省各子区域供水、需水约束条件,采用区域发展的协调度指标,并且能够对生态环境、社会、经济相互协调程度进行反映[8]。区域发展程度可通过对协调度最低值的设定进行表征,其表达式如下:
(13)
其中:
(14)
(15)
(16)

2.3 综合权重系数
对多目标问题的优化即为水资源配置的实质,确定多目标的权重系数就是对模型中不同目标的重要性进行有效的判断。熵权法作为一种客观权重计算方法,主要是根据指标包含的有效信息和重要性程度确定指标权重。本文对水资源多目标的权重系数考虑采用客观与主观相结合的方法进行确定,并成为综合权重,求解过程如下。
(1)首先设定评价对象有m个,评价体系中包含的指标数总数为n,表达如下所示X=(xij)m×n;(i=1,2,,m;j=1,2,,n)。
(2)因不同评价指标之间的量纲和单位存在一定的差异性,为消除量纲的差异对评价结果造成的误差需对判断矩阵进行统一规范化处理,并得到相对隶属矩阵:R=(rij)m×n(i=1,2,,m;n=1,2,,n)。
经济型评价指标其计算结果越大则评价越优,经济型评价指标的相对隶属度可采用下式进行计算:
(17)
成本型评价指标其计算结果越小越优,此类评价指标的相对隶属度可采用下式进行计算:
(18)
式中,rij—相对隶属度;(xij)max、(xij)min—在不同方案中同一评价指标xij的最大值和最小值。
(3)结合评价指标熵值的具体含义,各评价指标熵的确定可按下式进行计算:
(19)
(20)
式中,Hi—评价对象中第i项评价指标的熵值;fij—第j个评价对象的第i项指标权重占评价的权重值。
根据上述计算结果可对各评价指标的熵权W求解,如下:
W=(ωi)1×m
(21)
(22)
式中,ωi—各评价指标的熵权,取值范围为0~1,所有评价指标的熵权之和为1;W—熵权特征向量。
3 实例应用
本文以辽宁省水资源优化配置为研究对象,对目标综合权重利用上述方法进行确定,并采用可变步长萤火虫算法求解模型。
参考国民经济行业分类和各行业对生态环境、社会、经济的贡献值确定单因子隶属度,并利用各单因子评价结果建立相应的矩阵进行熵权、权值的计算,得到客观权重,然后通过邀请专家对各指标的相对重要性权重进行打分,以打分平均值作为主管权重[9- 11]。利用文中所介绍的综合权重计算方法得到相应的组合权重,结果见表1。
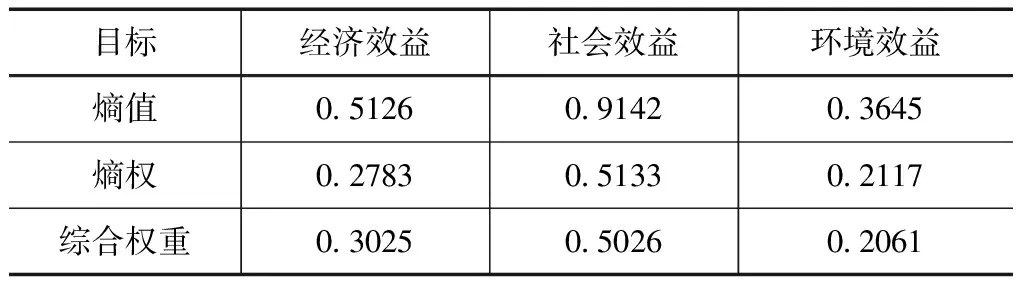
表1 多目标综合效益值
3.1 模型参数确定
在确定模型参数时应充分考虑研究区域水资源实际状况,部分参数参考相关文献资料。其中萤火虫更新因子选取为0.6,萤火虫迭代次数为2500次,动态决策域更新率和荧光素挥发因子分别选取为0.07与0.4。
3.2 结果分析
结合辽宁省往年供水与需水量有关资料,分别对该区域2020、2025、2030年的需水量与供水量采用指标分析法进行预测。对辽宁省2020年75%保证率条件下的水资源综合效益最优解分别利用可变步长萤火虫算法和基本遗传算法进行求解。结果显示,在达到稳定最优解时,基本遗传算法需要迭代次数为1520次,而萤火虫算法需要1060次。由此表明,相对于基本遗传算法,本文采用的可变步长萤火虫法具有更快的收敛速度。
分别对50%、75%保证率下各水平年水资源优化配置模型采用萤火虫算法进行求解,结果见表2。

表2 不同保证率下各水平年水资源优化配置
由表2计算结果可以看出,综合效益在相同水平年随保证率的增大呈现出一定的上升趋势,由此进一步表明在环境、社会、经济方面水资源优化配置呈现出更加和谐的发展趋势。另外,不同保证率下社会效益在2020、2025、2030年均表现出增加趋势。在实际供水量变化不大的情况下引起缺水率增加,因此为提高水资源综合效益和利用率迫切需要进行科学调水、节约用水等措施降低对水资源的浪费,并促进社会经济与水资源的和谐可持续发展的综合目标[12- 13]。
4 结语
本文设定模型中萤火虫更新因子选取为0.6,萤火虫迭代次数为2500次,动态决策域更新率和荧光素挥发因子分别选取为0.07与0.4,结合辽宁省往年供水与需水量有关资料,分别对该区域2020、2025、2030年的需水量与供水量采用指标分析法进行预测,得出的结论如下。
(1)在达到稳定最优解时基本遗传算法需要迭代次数为1520次,而萤火虫算法需要1060次。由此表明,相对于基本遗传算法,本文采用的可变步长萤火虫法具有更快的收敛速度。
(2)综合效益在相同水平年随保证率的增大呈现出一定的上升趋势,由此进一步表明在环境、社会、经济方面水资源优化配置呈现出更加和谐的发展趋势。
(3)在实际供水量变化不大的情况下引起缺水率增加,因此为提高水资源综合效益和利用率就迫切需要进行科学调水、节约用水等措施降低对水资源的浪费,并促进社会经济与水资源的和谐可持续发展的综合目标。
