牛顿力学的先驱惠更斯——机械论的数学化

付丽萍 陈玠同 姚珩

(1. 闽南师范大学物理与信息工程学院，福建 漳州 363000； 2. 台湾师范大学物理系，台湾 台北 11677)

毋容置疑,力学的核心是牛顿三大运动定律与万有引力定律．然而,它们是如何建立的?牛顿又是受到什么样的影响而提出来?现行的教科书中都未给予说明．经典物理学或牛顿力学是结构严谨、论证完整的科学思想体系,它不可能靠一个人在有限的时间内完成．牛顿的确是经典力学的集大成者,但是他如何逐步奠定起当代有效的力学思维与内容,则需要我们认真的研究与慎思．牛顿本人也明言他是站在巨人的肩膀上,才能看得更高更远,那么这些巨人是谁?他们的主张是什么?为什么可以深深地激励牛顿,促使他能够建立起稳定有效的力学架构．本文追寻牛顿力学的脉络,旨在教学中使教师们的思路更加明晰,提升学史素养．

1 伽利略的数学观

爱因斯坦认为伽利略(G.Galilei, 1564—1642)是近代物理学之父,而我们对其印象是比萨斜塔落体实验,因此认为伽利略是物理实验的开创者,但至今并没有任何史实资料可证明他做了比萨斜塔落体实验．然而,在其生前1634年最后一本著作《两门新科学的对话》的确有着详细记载的则是斜面实验,该实验指出物体下滑的距离(s)是与时间(t)平方成比例[1]

s∝t2.

(1)

图1 物体做匀加速度运动的距离与平均速度的关系

但该书是以定义、定理、命题与证明等几何学形式所写成,逐步说明如何有上式的结果,而非从斜面实验的数据分析得知．在全书51个命题中的第一个定理,开宗明义写道(如图1)：“从静止开始做匀加速度运动的一个物体,通过任意空间所需时间,等于此物体以最大和最小速率平均值的匀速度运动,通过该空间所需的时间．”[1]

若用现在的公式表示,即代表匀加速度运动物体的位移

(2)

其中v0与vt分别代表物体的初速与末速．利用此关系,可建立(如表1)得到在第1s,2s,3s……,每秒内的行进距离比为1∶3∶5∶7……,然后得知随时间增加,累积的距离比为1∶4∶9∶16……,即为上式(1)s∝t2．接着他用斜面实验来加以验证(如图2所示)．[2]

表1 匀加速度运动v ∝t,会有s ∝t2关系

图2 斜面上滚动的球每秒之间距比为1∶3∶5∶7∶……

伽利略深信地球上落体的运动必定遵循着最简单和谐的数学关系,而落体速度变化的最简式就是与时间成正比的关系,即

v∝t.

(3)

伽利略以复杂世界背后这种简洁的数学结构,可反应出真实的落体运动现象的信念,作为他全部物理学的思考基础．他曾不断多次强调:“(实验)完全是不必要的．对于我自己纵使没有做实验,我也确信就像我告诉您的一样,因为它必定得如此”．“借着发现某一事实的原因,来获得其知识,它可提供理解和确定其他现象的思维,并不需诉诸于实验”．“只有在数学中才能找到坚实的证明,这种力量让人充满惊奇与喜悦”．[1]此处所反映:大自然本身是按着最平常、最简单和最容易的手段进行各种变化过程的观点,被物理史学家视为是促成16世纪科学革命的重要因素,此思潮被称为“物理学的数学观”或“新柏拉图主义”．[3]伽利略首先将数学的和谐性引入物理学,使物理学脱离了自古希腊亚里士多德所主张应以“性质”(nature)来描述物理学的传统,[4]同时也改变了物理学的整体面貌．

2 笛卡尔的机械论

伽利略之后没多久,出现了一位绝顶聪明的科学家,也被称为近代哲学之父·笛卡尔(R. Descartes, 1596—1650)．由于老师们所教的他很快就懂;但他知道的,老师们却不一定懂,于是他开始怀疑书上所写以及前人所说的全部知识,而提出了“我疑故我思,我思故我在”的名言．因此他尝试着去寻找最不可怀疑的事物,以便从那奠立起知识的基础．后来他发现虽然每件事情皆令人质疑,但有一件事却永远无法怀疑,那就是“三角形之内角和为180°”,亦即只有几何学为不可质疑的真实之物,他于是从几何学的点、线、面开始来建立起物理学的知识．由点、线、面可形成长、宽、高,也就是占有空间的延伸物,或称作物体(body)．换言之,应该从这种不可穿透、坚硬的物体做为科学知识论证的根基．若物体缩成很小之物,它便可称为质点(particle),他并坚定认为“一切的感觉现象皆是来自物体或质点的位置改变(即运动)所形成．”此种主张后来被称为“机械论”(mechanism)．[3]笛卡尔用此观点诠释了光的反射、折射、气压与磁铁的吸引排斥．他并描述了做圆周运动的物体的特征如图3,绳上的球或木杆上的蚂蚁都具有离开原本的B、F点朝向C、G点运动的特性,且称圆周运动上的物体皆具有此种逃离圆心之性质为离心趋势(endeavor),或离心倾向(tendency)．[5]

图3 笛卡尔离心趋势图

图4 笛卡尔涡漩理论之模型

他更以此性质来解释行星的特殊轨道(图4)．笛卡尔认为宇宙间布满了流体般的以太(ether)物质,在快速移动下形成了许多涡漩环流,在涡旋边上的行星都倾向逃离中心,而此行星也会受其他不同涡漩的作用,最终有些地方所受各种涡漩的离心倾向可互相抵消,达到平衡,而确定出行星的轨道．[5]以现在的观点来看,此涡漩模型相当粗糙,然而在笛卡尔之前宇宙是分成月亮之下的变化世界,与月亮之上的完美天体,结构迥异．他的涡漩理论在历史上则是首次以日常所见现象来诠释天体运动,它打破了古希腊与中世纪时期所主张天际与地表明显区分的传统宇宙观．[6]

3 数学观与机械论的冲突

新柏拉图主义的数学观主张以秩序处理现象,满足于发现某种精确的数学描述,并将这种描述理解为对宇宙终极结构的一种表达．机械论关心的则是许多个别现象的因果关系;自然界对人的理智是透明的;试着消除生机(vitalism)哲学中的各种蒙眬,并证实自然现象是由不可见的、类似于日常生活中人们所熟知的机制所引起的．此二思潮由于追求不同的目的,常导致彼此相互冲突．对机械因果关系的阐述常常站在与通向精确描述之路相反的方向上;同样,精确的数学描述却无法提供现象背后的成因．[3]

例如，伽利略发现重物轻物皆会以相同加速度落下,并可精确描述其速度、位移与时间之关系,却无法说明是什么原因造成?行星运动准确地遵循面积律与椭圆轨道,但无法通过机械论解释为何会有此性质?同样的,笛卡尔可以说明行星会有特殊的运动轨迹,却无法精确地指出为何是椭圆?只有尽力或完全消除两种观点间的不一致,物理学才算充分完成．

4 惠更斯的创见：机械论的数学化

4.1 重性的机械论解释：重性是离心力的结果

面对这些重大的困难,荷兰物理学家惠更斯(C. Huygens, 1629—1695)是第一位将机械论与数学方法结合在一起的智者．他首先以机械论观点说明重性—为何重物会下落的原因(重性gravity并非重力,因当时尚无引力观点)．惠更斯依循着笛卡尔,认为地球附近所充斥着隐含的以太,就好似图5中管内充满的水．当管子沿中心轴A旋转时,由于管内水的离心趋势作用较大,会朝管端P移动,而将木栓B压向管底．重性便是在一个充满以太物质的涡旋世界中,一些离心趋势较弱较缺乏的物体,由于受到离心趋势较强的以太物质作用,导致重组与碰撞,而被迫落向中心或拉向地心,遂形成物体坠落现象,因此重性是离心力所造成的结果．[7]

图5 木栓B放在充满水的管内,当管旋转时水会往外推至P点,而木栓将朝管底运动

4.2 离心力的量化

为了要说明重物下落距离皆会与时间的平方成正比,以及此结果是由地球旋转带动以太物质的离心力所造成．惠更斯聪颖过人,以独到的见解与特殊的直觉,开创出了将机械论所主张的离心力加以数学化的处理方法,影响深远．惠更斯的想法最先出现在1659年的手稿,正式发表于1673年《摆钟振荡》(The Pendulum Clock) 论文的附录中,但里面只有结论无任何证明,在逝世后的1703年,后人代为整理出《论离心力》(On Centrifugal force) 的论文中,则有详细的论述．[8]他的论文有17个假设,其中最重要常见的为下面的3个假设．首先,他定出离心力的大小,认为物体若不受任何干扰时,如笛卡尔所言,它将维持直线前进．但在圆周上,做圆周运动的物体总有一股倾向,欲脱离圆弧,回到开始时直线的趋势,此趋势称为“离心力”,其大小为EG长度(图6)．他接着宣称以下假设.

假设1:假如两个一样的物体在相同时间内完成不同的圆运动,则大圆的离心力会大于小圆的离心力．[8]

图6 惠更斯假设1示意图:在相同周期下,

不同圆周上物体的离心力与半径成正比

假设2:假如相同的物体在同样的轨道以不同的速率做旋转,但两者都是做等速率运动．其远离中心的力,速率快的物体会比速率慢的物体还要大．也就是说,假如以绳线系住物体并从桌面穿过圆心,另外一头悬挂重物,而此物体的重量会等于所抵抗的离心力,且重量大小与速率的平方成正比(如图7)．[8]

图7 在同一圆上,离心力与速率平方成正比

假设3:假如两个相等物体以同样的速率分别做不同大小的圆周运动,它们的离心力会与直径成反比,所以小圆的力会比较大(如图8)．[8]

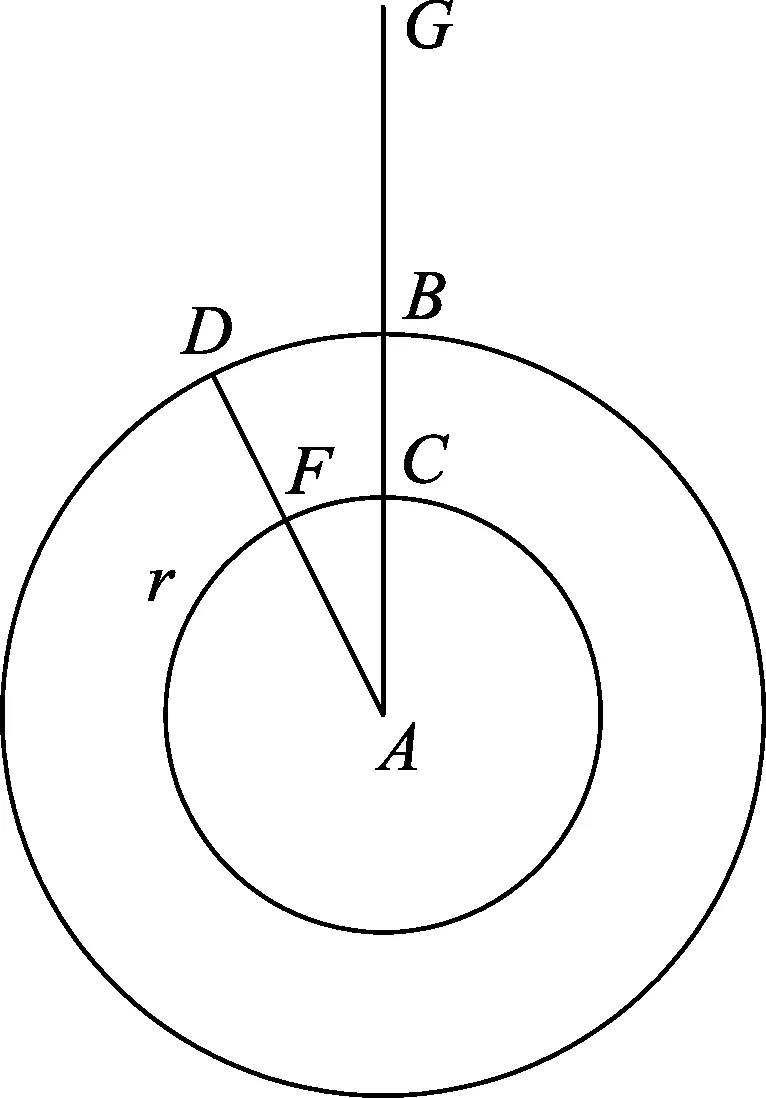
图8 速率固定时,离心力与半径成反比

若以F表示离心力,r表示圆周运动半径,ω为角速率,v为线速率,则假设1表示ω固定时,离心力与半径成正比

F∝r.

(4)

假设3表示v固定时,离心力与半径成反比

(5)

假设2表示r固定时,离心力与速率平方成正比

F∝v2.

(6)

此3个假设若结合在一起,就形成后来所言离心力F与r、ω、v之关系为

(7)

虽然,圆周运动在早期托勒密(Ptolemy, 100—170)与后来哥白尼(N. Copernicus, 1473—1543)的天文学都曾充分探讨过,但都是以行星为对象,且从未有作用力的观念．惠更斯是第一位将圆周上运动物体与所受的作用力结合,并提出精致的力分析的物理学家．最初惠更斯并未写下上述命题的证明,但他对离心力别出心裁的处理方式与数学运算,已大步迈出当时机械论者的思想局限,也开拓了物理学家的视野,并深深启发了牛顿．[9]今天的教师们在讲授圆周运动物体与力关系时,其实就是在使用惠更斯的理念与做法．

4.3 落体下落距离与时间平方成比例

利用以上3个假设,惠更斯接着描述到(如图9):“当一个物体在B点被释放,做匀速率圆周运动到达E点时,有回到C点的趋势,到达F点时,有回到D点的趋势．这将会造成一个物体从原本位置沿着连心线离开中心的趋势．以这种方式在第1段时间它将会以EC之距离远离,在第2段时间会以FD之距离远离．而这些EC、FD之距离,以及其他时间内的距离会以时间平方的方式增加,即它们的比例将会是1、4、9、16…….物体的重性是同体积的以太物质以非常快的速度离开圆心所产生的效果．以太物质不断地向后退去,并尽可能沿着半径方向离开圆心,而使得物体掉落．”[8]

图9 离心力所造成的位移量之比

惠更斯没解释此段论述的原因,在此稍加说明．[9]如图10,做圆周运动的物体,自B点移动至E点,EC长代表所受离心力．利用弦切角∠CBE=圆周角∠CTB,加上公用角∠C,可得△CBE～△CTB,对应边成比例给出BC∶EC=CT∶BC或BC2=EC·CT,而在极短的时间间隔内CT则近似于直径．再参考图9,物体自B点行经至F与M点所需时间,分别为行经至E点所需时间的2倍与3倍,即BC∶BD∶BS≈1∶2∶3,最后可得EC∶FD∶MS=BC2∶BD2∶BS2=1∶4∶9．

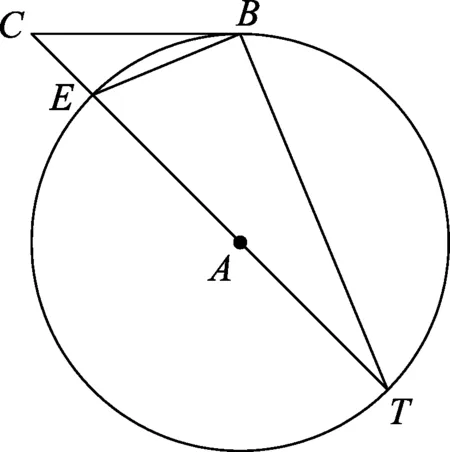
图10 离心力EC与BC2成正比

因此,做匀速率圆周运动的地球会带动其周围的以太脱离其原来位置,且以太沿着连心轴随着时间向外离开其原来位置的距离,会与时间平方成比例．其腾出的空缺,将导致物体持续予以填补,此种效应不但会造成物体下落,且其下落距离也会与时间平方成比例．

惠更斯便是如此,从机械论中以太的离心趋势或离心力出发,引入细腻的数学规划程序,先将离心力的概念量化,再透过有效的运算分析,合理推导并诠释出伽利略落体运动的和谐关系．这种创新与彻底的数学方法,不仅解除了数学观和机械论冲突的鸿沟,并在论证过程中将此两种不同的思考模式交互使用,获得许多有意义的成果．这种将原本差异甚大的两种思潮圆满结合——先分析力作用情形,然后使用数学运算,最后寻找出和谐的形式结果的方法,从此一直沿用至今．[3]

5 对牛顿的影响

惠更斯将机械论数学化的划时代创举,获得年轻牛顿的高度赞许,1669年牛顿在《论圆周运动》一书中,[9]写下非常重要的规律 (参考图10,事实上它正是牛顿所绘所用之图):在时间BE中,物体B离开圆心A的离心趋势与离开圆周的距离EC成比例,……有如在无阻力作用时,相对物体在此段时间可自由沿着切线移动,两者所造成的变化距离,且

EC=BC2/CT.

(8)

此处BC表固定时间之位移,即速率,若在很短的时间下CT即为直径或2倍之半径,也就代表着离心力EC或F∝v2/r,这关系就是前面惠更斯所述3个假设的意义．而此规律是促成牛顿日后发现万有引力的核心关键,但它却完全是惠更斯的主张与方法．

牛顿当时也应用了上述规则,开始探讨落体的重性,与做圆周运动月球之离心力两者之间的关系,并在1669年如此陈述:“我以月亮至地球距离为地球半径之60倍……则地表的重性为月亮被拖离地球之离心力的4000倍.”[9]

此段话也呼应了他自己所说，距离平方反比律在他20多岁时便有了正确想法,所指的即是式(8)与式(7)离心力结果的延伸,而此论述基本上正是遵循着惠更斯的思考方式．代表牛顿不仅接受离心力的概念,更重要的是在思维上发挥了惠更斯所开启的机械论的数学化方法．由此可知,在牛顿提出3大运动定律与发现万有引力之前,即在40岁左右发表《自然哲学与数学原理》之前,[10]惠更斯的思想一直深刻地影响着牛顿,并处处反应在其著作里．直至牛顿受到胡克(R. Hooke, 1635—1703)向心强度(central attraction power)的启示,终于在1684年提出了向心力(centripetal force)的概念,再配合开普勒(Kepler, 1571—1630)的行星周期律,才获得正确的引力定律及丰富的研究成果,此时他在力学上的贡献才真正超越了其先驱—惠更斯．[11]

6 教学启示

牛顿力学的建立不是为了解决工程问题,它是一种思想创见,[10,12]是要挖掘自然现象背后所蕴含的原理,正确诠释运动与变化的成因,进而预测与发现可能的新现象．牛顿的运动定律与万有引力定律是奠立在伽利略的数学观、笛卡尔的机械论与惠更斯的离心力的数学化,是经过长时间的历史传承与自我创新,所获得的知识体系．既是渊源流长,也是无可取代,才成就了今日经典力学完美的形式与内容．

然而,在有限的教学时间里,教师们往往传授的是已完成的结论,教学重点放在了如何正确运用物理知识,去应用与解决相关的科学问题．教学的关注点也放到了中考、高考的考点上而很少去“追根溯源”．物理学为何以这样的风貌展现?它是如何建立起来的?又为何必须是如此?教师们如果清楚了它的源头与成因,将会更有信心带领学生如何去思考,且高瞻远瞩,有所坚持便会“言之有物”．学生们在这种潜移默化的熏陶下,也会追根究底,习得有效深刻的思维方法．