自行车稳定前进时的某种表观几何现象

(上海市位育中学，上海 200231)

1 引言

两轮自行车一直被认为是一个很神奇的东西,依靠与地面的两点接触,竟然可以稳定运行而不倒下,同时具有比三轮或者四轮更大的灵活性．对它的平衡原理有过很多研究,这里不再赘述．笔者在使用自行车时,遇到一次龙头突然卡住的情况,几乎立即摔倒,由此思考:如果有平衡状态,龙头不动也应当有可能稳定运行一段时间,但事实上是没有人骑车时能做到,那么会不会自行车的骑行是一个长期稳态而非平衡态呢?

2 问题

只有两点接触地面时,除理想状态外根本不会有平衡,现实中也会发现骑车时,即使直线前进车身也不可能一直保持竖直,而多多少少都有左右摆动,如图1,沙滩上的轨迹清楚地证明了这一点．为什么骑车时要不断地微微转动龙头而引起车身的摆动呢?而且看起来这种摆动还具有一定的节奏性,比如与蹬车的周期相同．由于提出的是一种基本设想,这里将对模型尽量简化．

图1

3 圆周运动和前轮微摆模型

图1可见自行车是不断地左右微拐弯前进的,那么必须建立拐弯时的圆周运动模型．图2(甲)从侧面将车架简化为连接两轮(虚线圆圈)圆心的长为d的刚性倒T形架,而人和车的总质心G固定在车架中央上方,距离地面为h．轮子与地面的接触点为P1、P2,距离也恰好是d,P为这两个接触点的中点,且假定车是从P2向P1方向前进的,这种模型只能侧倒．当正常微左转时,从正后方看过去如图2(乙),设定P点为整体的等效支点,模型被进一步简化为一个重球支在一根轻杆上,此时向左偏离竖直线α角,由于该角很小,质心离地高度仍近似为h,而δP为此时质心相对于P在水平方向的偏离量．当采用P的圆周运动作为参考系研究时,质心受力如图(地面作用力未画出),其中F为惯性力,在该参考系中不倒即关于支点P力矩平衡及几何关系得

(1)．

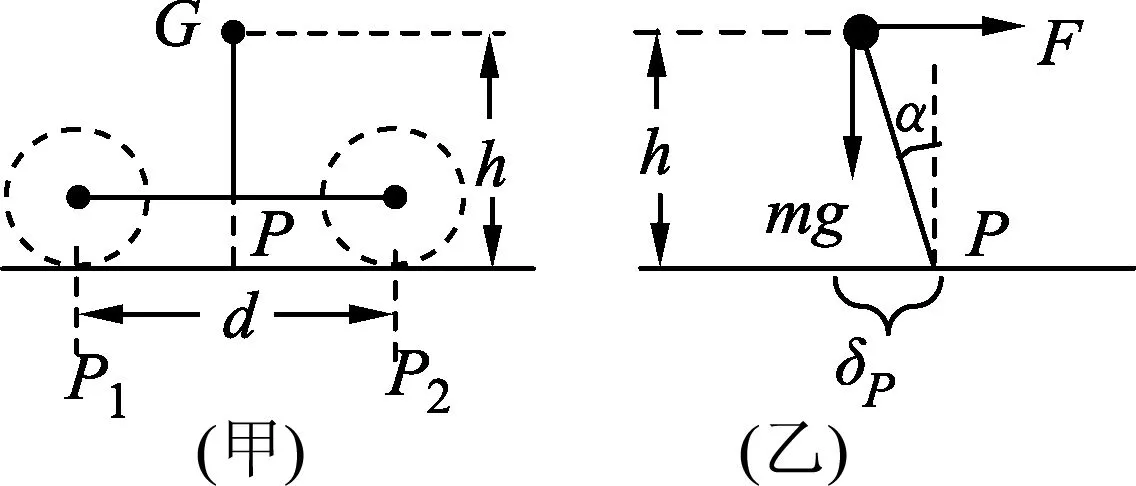
图2

图3

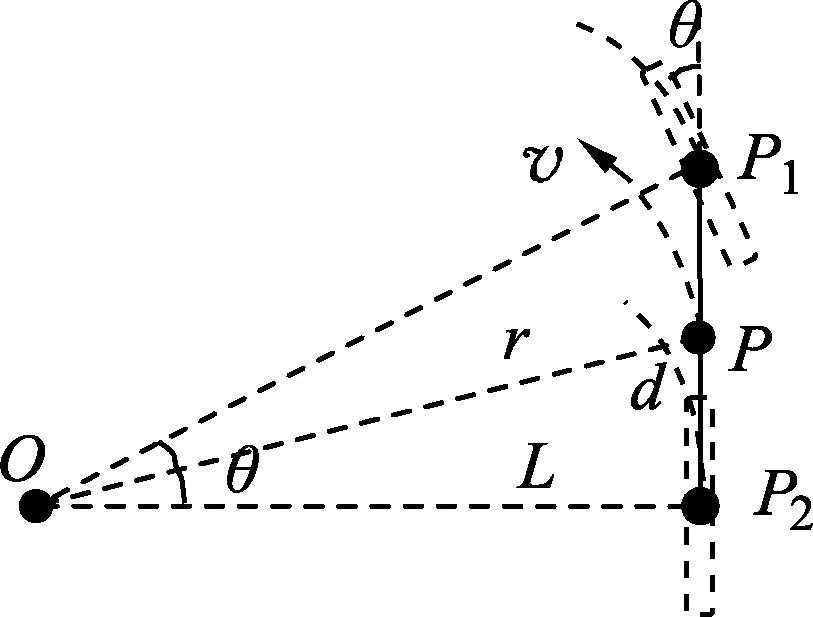
图4

主导车行进方向的是前轮,图3是实拍稳定运行时自行车前轮向左和向右微摆动的瞬间(因车有故障而不是很对称),说明前轮与车身的夹角确实存在,几何关系则需从俯视图建立左转模型如图4,虚线窄长方框为两轮,前轮向左微摆,将其与车架所成角度θ称为摆角,假定为固定转弯过程,则车身上各点的轨迹应共用相同的圆心O,相当于一个三角板OP1P2在绕O点转,由两轮运动方向平行于轮本身,可知两个地面接触点的运动半径OP1和OP2的夹角也是θ,且θ角很小时可近似认为

(2)

将车速v近似看作P点圆周运动的线速度,其半径为r,则前面的惯性力即为

F=mv2/r.

(3)

4 支点移动模型

自行车稳定前进时为什么要微转弯呢?

用一根长而轻的杆顶着一个重球长时间不倒下是可以做到的,比如杂技顶杆,秘诀就在于支点的移动,也就是当重物有些向左偏倒时,快速地向左移动支点,在偏得更加严重之前,支点已经到了重物左下方的位置,那么此时杆对球的作用力沿杆朝右上方,会阻止重物的继续左移而促使重物向右偏倒,于是再将支点快速右移以阻止右偏的发展,以此类推,让重物在不断地左偏右偏中维持了一个相对的稳定而没有倒下.这里仅从地面参考系说明支点左右移的目的,所以不再出现惯性力的考虑．而此情景正是图2(乙)视角所看到的自行车身的简化运动,所以自行车的稳定亦来自支点(等效)的移动,而且这种移动绝对不是打滑,而是在移动中需要怎样的作用力,地面能就给予怎样的力,就像顶杆时用手控制杆子的底端一样,此即支点具有合理加速度的原因．

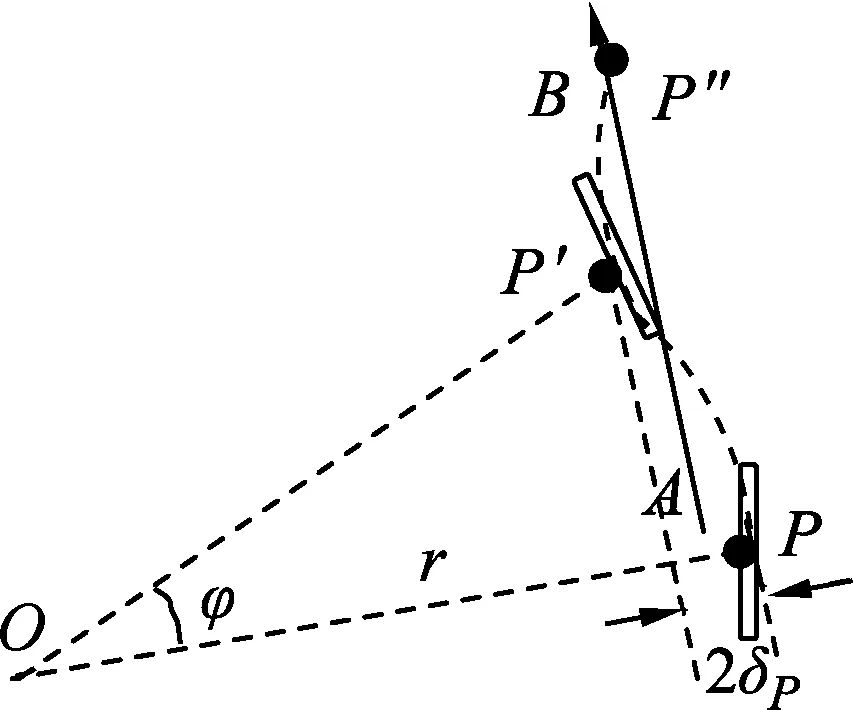
图5

自行车与地面的接触点(相当于顶杆中的支点)不能平白无故地侧移,否则就是打滑,因此这种支点的左右移动便由转弯来实现．现在把车轮略去,俯视图进一步简化为图5,虚线曲线PP′P″为大致的P点轨迹,那么前进方向基本为AB箭头方向,在一段时间内,假定前轮保持着θ摆角(其实这个过程中摆角是变化的,为了简化计算认定θ不变)使等效支点P移动到P′处,半径OP转过角度φ,且恰使图2(乙)中P点偏离质心从最右到最左,故有P点的侧移量为2δP,满足2δP=r(1-cosφ)=2rsin2(φ/2)．而当θ角很小时,φ也很小,近似有sin(φ/2) ≈φ/2,故2δP≈2r(φ/2)2=rφ2/2．

同时,把左右脚各蹬一下认为是稳定骑车时的周期T,也就是车身摆动周期,不难理解P到P′的过程就是T/2,则有φ=vT/2r,即T/2经过的弧长除以半径,代入上式消去φ有

(4)

回到前面,由(1)、(3)、(4)式消去δP可得

(5)

取h=1 m得到T=1.278 s,是个合理的蹬车周期(真实过程中θ会变小,转弯效果削弱,完成2δP需要更长的时间,而恰好真实的舒适周期在1.5～2 s),合适的惯性力体现圆周运动的稳定性,因此可把(5)式看动力学方面人感觉较稳定的质心高度和蹬车周期的关系式．所以加速时(即减小T),往往采取更低重心的姿势(即减小h)会更舒服．

换一个思路,由(2)、(4)式消保留δP消去r得

(6)

将(5)式代入有

(7)

取h=1 m,d=1.2 m,v=5 m/s,δP=0.04 m这些现实中比较合理的数据,得到θ≈1.08°,这个夹角计算值符合实际情况,在很稳地骑车时,前轮与车身的夹角极值就是两度左右．图3的左右偏角加权平均较大是因为单手骑车且龙头不灵活,所以不是很稳．

是否能根据(6)、(7)式判定,车速越快时对应的θ一定越小呢?其实车速与周期成反比,可以令v=k/T,k为厂家设定的系数,则(6)式成为

(8)

上面数据对应系数k=6.39．(7)、(8)两式表面存在矛盾,一个与车速有关而另一个无关,但仔细思考(7)式的来源(5)式,表征的是圆周运动,在起步阶段,车速过慢,车身不倒很大程度上取决于圆周运动的稳定,所以(7)式起到决定性作用,因此确实一开始的前轮摆角是很大的.这也是个不太稳定的过程,近似也不能很好地成立,所以这里并未过多研究．

正常骑行时速度足够且轨迹较直,圆周运动不太明显,而支点移动的硬性标准指向(8)式,且各种近似得到很好地满足,所以如果δP比较恒定时,骑得稍快或稍慢一些前轮的摆角是差不多的.且根据前面的论述,车速稍大时通常会稍微降低重心,减小h,所以(7)式也能指向摆角变化不大的结论,并不与(8)式矛盾．

当骑得很快时,又会发现前轮摆角θ是个更加小的值,几乎与车身一起动,而且感觉挺稳,想摔倒都不可能,但这时的蹬车周期T变得比正常小不少,会与(5)式偏差太多，因为h不可能大幅度减小,怎么理解这样的稳定呢?事实上在蹬车周期太小(比如小于1 s)时,会发现车身的摆动周期自然地变成蹬车周期的两倍(2 s左右),即摆到左边蹬两脚,摆到右边再蹬两脚,不再是一边各蹬一脚,而我们要用来推导(4)-(6)式的正是车身摆动周期,2 s左右的周期与(5)式相差不大,而最后(8)式中相当于k变为原来2倍,即分母会乘以4,侧移量δP虽然也变大但没有大到4倍,结果是车身摆动幅度变大、节奏变慢,但前轮摆角却更小．这种情况不作过多展开．

以上推断均有实际经验和事实,定速车在骑得很快时摆到一边只蹬一脚会导致车身很剧烈的晃动,要摒除这种不稳定性但又不想一边蹬两脚的话,就得使用变速自行车,通过k的调节形成高速下仍有合适的蹬车周期,等于(5)式中的车身摆动周期．

5 其他分析

(1) 为什么在溜车(不蹬)时没有太多的前轮摆动节奏感?因为溜车时不存在蹬车周期,整体质心相对于等效支点的偏离很随机,所以人会随机地用龙头带动前轮摆动,其感觉不如骑车稳定．同理自行车慢速比赛时也存在类似的问题,人和车因扰动而导致的质心与支点的偏离总会存在,但前进速度很慢时,想及时有效地侧向移动支点变得更加困难,所以很容易摔倒．

(2) 为什么成人骑童车会感觉不好?童车不是小轮自行车,骑童车的成人比正常情况重心更接近地面,倒下得更快,且厂家设定童车有较小的车速周期比k,导致成人不得不更迅速地蹬车,同时根据(8)式,虽然其车架d也较小,但仍可能导致需要更大的θ角,结果就是更快的摆动及更大的摆角,加上伸不开腿,所以缺乏习惯中的稳定感,当然,儿童是很习惯快速蹬车的．因此不论车轮大小,成人骑车较舒适时总有一个合适的座位高度及变速比(对应k、T)．

6 深层研究

(1) 人体感官:如何形成质心的节奏性偏离等效支点?见图3,如果是很轻松正常地骑车,我们会发现通常抬左膝时,会自然地控制龙头带动前轮向左摆动,这个动作的起始阶段可以体会到人身体重心的左移．同时此动作右手前伸,与走路出左脚伸右手的平衡相统一,从自然规律上减少了人的不稳定性．再结合图1可知,支点相对质心水平位置的偏离及其变化一大部分是来自于车身的摆动,进一步降低了人体的摆动感．如果将这个动作反过来,硬是抬左膝且向右摆龙头,就是同手同脚的感觉,会加大摆幅,不稳定,但在短时间加速过程可以接受这种用力方式．

(2) 车身研究与因果关系:在舒缓地骑车时,前轮的摆动来自于人体本身的节律性带动,则车身的侧倾及转弯就是由前轮带动的结果．但当车速较高时,前轮的摆动似乎并非人手控制,而是车身平面侧倾后,带动前轮摆动,因果关系恰好相反,比如图6这种危险的空手骑车情况,如何理解这种摆动机制?

图6

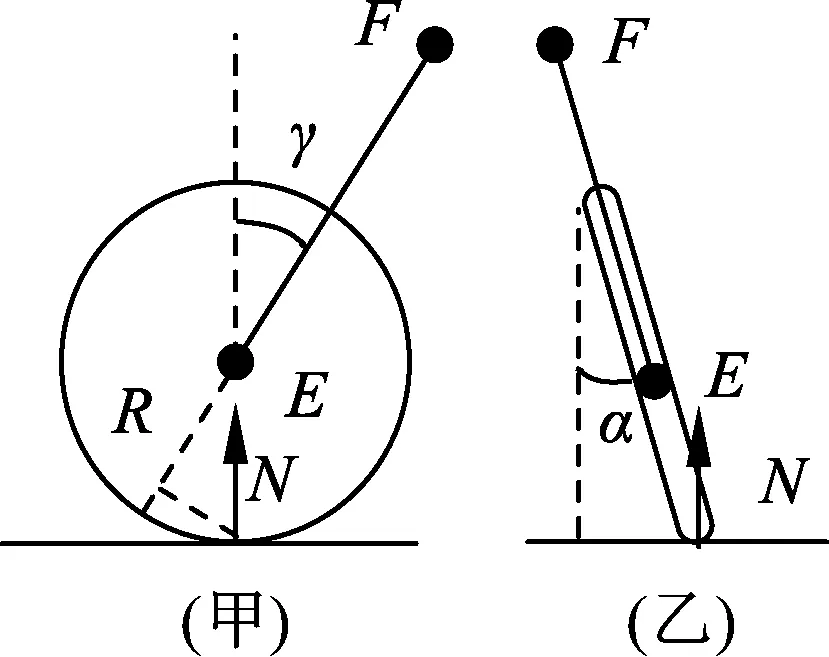
图7

仔细观察当今绝大多数自行车前叉都是向前下方控制前轮,不是竖直向下,这个设计在车身平面倾斜时,会对前轮产生一定的力矩效果．如图7(甲)所示,车轮半径为R,EF代表前叉,车身竖直时它与竖直线夹角为γ,而图7(乙)是从车正后方看过去的视角,车身平面偏离竖直面α夹角,这时若以EF为转轴,沿前叉从F向E看过去,地面的支持力N将产生逆时针力矩(立体关系此处未画出),满足(用N垂直于轮平面的分量乘以关于转轴EF的力臂)

MN=NsinαRsinγ.

(9)

现实中自行车停放时车身向左倾,这个力矩会立即使前轮左摆,正好符合前面左转弯模型的要求,即车本体结构也可以贡献出正确的前轮微摆动效果．轮子的重力及前叉的作用力对EF轴无力臂,而此时是前轮刚偏,车的圆周运动不明显,所以也忽略了地面给予摩擦力的侧向分量．所以前叉设计天然地符合了前轮微摆的方向性要求,同时增大跨度,提高了车身前后方向的稳定性,并可以容纳更大的前轮,方便提高车速,可谓一举多得．

N作为地面的支持力其实仅与人、车的重量有关,可认为与厂家设计的γ一样是定值．单独看R越大时,一般可以使(9)式的力矩增大．其实这个力矩本身很小,但是考虑到θ和周期的量级,只需让前轮带龙头有很小的角加速度就可以了,所以还是合理的．但是更需要应对的是地面和龙头轴等方面产生的阻力,如果这个阻力很大,那么我们需要更大的车身倾角α来提高力矩效果,这就很容易摔倒了;如果这个阻力是定值,那么对于小半径的轮子也是需要更大的车身倾斜度来达成足够的力矩,以促成前轮的摆动,所以骑小轮车不用手扶也是容易摔倒,而且小轮车的前轮受龙头惯性的制约程度较高,更容易出现前轮摆到一边就摆不回来的情况,所以骑小轮车的人很少是双手放空的．当然轮的尺寸很大时,根据人体有限的尺度,顺利摆动车身将变得很困难,所以也是不利于空手骑的．

7 角动量相关的研究

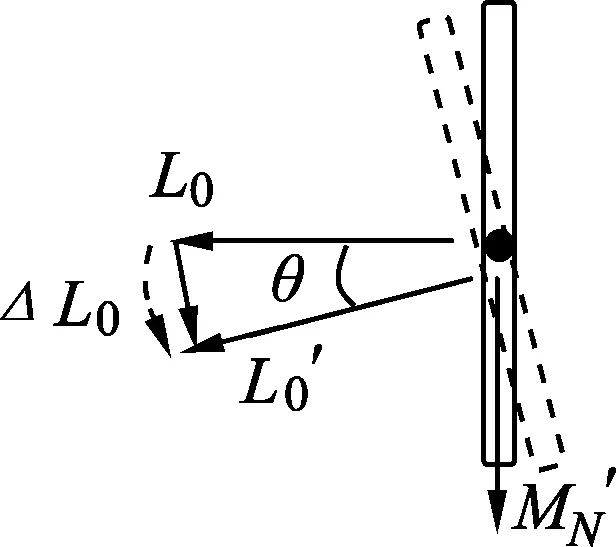
图8

我们不妨多研究一下车轮角动量受力矩影响的效果．将图7(甲)的前叉简化为完全竖直,此时车身(车轮平面)再怎么倾斜支持力都不会产生关于轴EF的力矩,不用手扶是否就无法使前轮以左转替代倒下了?在图7(乙)中选取过E点且垂直于纸面的转轴,N产生了一个向纸面外的力矩MN′=NRsinα,而此时前轮的角动量L0为向左略偏下,从FE看过去简化俯视如图8,该力矩将促使L0转向,导致前轮左转．现在略去龙头等其他结构,假定只有前轮,在恰当的周期T下,图8所示从中线左摆到最大的θ角 时间为T/4,则MN′T/4=ΔL0;小角度近似下ΔL0≈L0θ,轮子的质量m0集中在边缘均匀分布时有L0=m0vR,综合可得v=NTsinα/(4m0θ),再根据v=k/T和(10)式,可得

(10)

保守假设k=6.39,h=1 m,δP=0.04 m(其实因为不稳可能更大),θ=2°(已经够大),N=250 N(龙头阻力相当于削弱转向效果,故简单等效为取偏小的N),m0=2.5 kg,空手下形成恰当摆动且不倒需要的车速为v=13.53 m/s,与现实相差甚远,所以不大可能有人放空前轮骑竖直前叉的自行车,当然现在也基本找不到这样的自行车．注意,这个模型跟一个轮子或一个硬币自己滚动是有区别的,比如地面支持力不随轮大小而改变(主要取决于人和车身的重力)．如果是一个轮子自己滚动,那么(10)式中N=m0g会消掉分母的m0项,但这种情况下,T、h、θ、R等参量之间的关系也不再是自行车机制,(10)式也就不成立了,更深入精确地判断有待广大同仁进一步研究．

8 辩证与结论

轮子的大小和质量会影响角动量大小,有很大轮子的古董自行车和很小轮子的现代折叠车都可以稳定骑行,甚至没有轮子的雪地自行车也可以稳定滑行,所以用角动量相关的因素去解释稳定性就过于牵强了．圆周运动只是研究稳定因素的手段,我们可以假设在一艘慢速运动的航母上(相当于传送带)骑自行车,相对速度与航母速度大小相同,且方向相反,而那么从地面参考系看来自行车是不前进的,不存在转弯方面的圆周运动,但仍能稳定骑．不倒的实质应具有普遍性,如杂技中的顶杆运动,或者单脚冰刀前进等,都是利用支点的及时有效的移动来实现稳定,这就是为什么骑自行车无法以0的速度在路面上不倒,但却可以稳定在钢丝上,因为钢丝是可以随着人体左右摆动的,进而支点随之移动．如果以存在加速度的支点为参考系,人的感官平衡从力学上讲就是惯性力与重力的力矩平衡,所以不管有没有自行车前进中的圆周运动,都可以分析惯性力．这里的前轮微摆模型主要分析了等效支点的位置变化和蹬车周期等物理量之间的关系,得到了相对合理的前轮微摆偏向角θ的关系式并在现实中加以验证,说明了支点移动维稳模型的正确性和普遍性,也算是从某个方面展现了自行车稳定前进的一种机制．