地铁车站深基坑变形特性和突涌判定数值分析
2019-03-24何亮刘正明罗元喜
何亮,刘正明,罗元喜
(1.常州工学院,江苏 常州 213032; 2.江苏省地矿局第二地质大队,江苏 常州 213022)
0 引言
随着基坑开挖深度的增加,下部承压水会逐渐对基坑的稳定性产生影响,如处理不当,极易诱发基坑工程事故[1]。常州正在大规模开展城市轨道交通建设,出现了许多较深的基坑工程,承压水对基坑稳定影响的问题更为凸显,为此开展承压水基坑突涌稳定性的研究工作势在必行。
基坑抗突涌判定通常采用建筑基坑规范中的“压力平衡法”,但该方法只考虑承压水层和坑底之间隔水层重力抵抗承压水顶托力的作用,计算较为保守,应用于实际工程常常并未发现突涌[2]。因此,一些学者研究了考虑土体强度的基坑突涌判别方法,如均质连续梁板法和均质连续体法[3-5]。要想详细分析承压水对基坑突涌稳定性的影响以及基坑变形特性,采取有限元数值分析的方法更为有效,有限元数值模拟方法的关键是选择合理的土体本构模型和参数。小应变硬化土模型(以下简称HSS模型)是一种用于数值分析的高级土体本构模型,可以模拟包括软土和硬土在内的基坑变形特性,以及判定基坑突涌[6-12]。
本文基于室内三轴等试验获得的土体HSS模型参数,采用Plaxis软件开展了地铁车站深基坑开挖的有限元数值模拟,探讨深基坑开挖影响下围护结构和周围土体的变形特性,以及突涌判定方法。
1 工程概况
常州地铁二号线青枫公园站标准段基坑的开挖深度为17 m,宽度为22 m。地下连续墙深入地层29 m,墙厚0.8 m。坑内设置3道内支撑。第一道为钢筋混凝土支撑,支撑间距9 m,截面积为800 mm×800 mm。其他2道为钢支撑,支撑间距为3 m,第一道钢支撑直径800 mm,第二道钢支撑直径609 mm。
本工程基坑开挖深度影响范围内自上而下土层分布如下:①填土、③2黏土、⑤1黏质粉土夹粉砂、⑤2粉砂、⑤3粉砂夹黏质粉土、⑥2粉质黏土、⑧1黏质粉土夹粉质黏土层、⑨2黏土、⑨3黏土。第一层承压水位于⑤1、⑤2和⑤3层中,第二层承压水位于⑧1层。地连墙底部位于⑧1层中,它截断了坑内外第一层承压水的水力联系,因此基坑施工只需考虑潜水和第二层承压水的影响。潜水埋深位于地下2 m,第二层承压水埋深位于地下4 m。
2 基坑实际开挖工况的数值模拟
2.1 计算模型
根据三轴固结排水剪切、三轴固结排水卸载-再加载、标准固结和共振柱试验结果,将类型相同、基本参数相似的土层合并,获得各土层的莫尔库伦和HSS模型参数见表1。模型表达式、参数的意义见参考文献[8—9]。
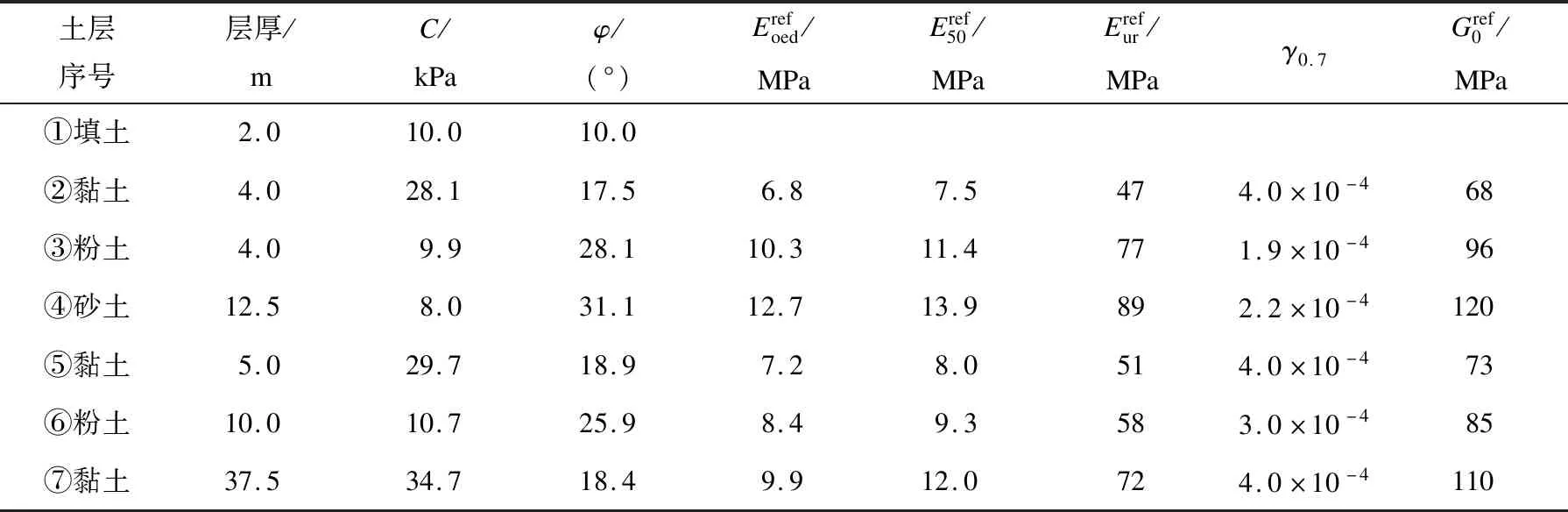
表1 HSS模型参数
根据基坑开挖实际工况,建立平面应变数值计算模型。
第一步:地下连续墙施工;
第二步:在-1.0 m处布置第一道混凝土支撑,并开挖第一层土至-7.5 m;
第三步:在-7.5 m处布置第二道钢支撑,并开挖第二层土至-13.0 m,降水将承压水头降至埋深17 m位置;
第四步:在-13.0 m处布置第三道钢支撑,并开挖第三层土至坑底处;
模型中地下连续墙采用板单元模拟,轴向刚度为EA=2.6×107kN/m,抗弯刚度EI=1.4×106kN/m2。内支撑采用点对点锚杆模拟,第一道钢筋混凝土支撑轴向刚度EA=2×107kN/m,第二道钢支撑轴向刚度EA=8×106kN/m,第三道钢支撑轴向刚度EA=2×106kN/m,第二道和第三道钢支撑施加的预应力分别为1 350 kN和2 350 kN。承压水贮藏在⑥粉土中,土层层顶埋深26.5 m,降水前承压水头埋深为4 m,施工降水后承压水头埋深为17 m,模型网格如图1所示。

图1 模型网格图
2.2 数值模拟和现场监测的对比
根据实际基坑的分步开挖施工工况开展数值模拟。HSS模型获得的土层水平和竖向变形云图、地下连续墙等值线图如图2、3所示(开挖到基坑底部)。得到以下结论:

总位移ux最大值=0.039 04 m(单元2376在节点13638)最小值=0.038 98 m (单元2689在节点25416)(a)基坑左半部分土层的水平位移

总位移ux(最大200倍)最大值=0.037 68 m(单元41在节点13641)最小值=-1.822×10-3 m(单元1在节点12883)(b)基坑左侧地连墙的水平位移图2 土层和地连墙的水平位移等值线图

总位移ux最大值=0.055 09 m(单元2719在节点20992)最小值=-0.028 00 m(单元549在节点9095)图3 土层的竖向位移等值线图
1)土体水平位移最大值为39.0 mm,地下连续墙的水平位移最大值为37.7 mm,均出现在坑底附近。
2)土体的竖向沉降最大值为28.0 mm,其中地表最大沉降为26.5 mm,出现在距基坑8 m附近位置;坑内土体最大隆起值为55.0 mm,位于基坑中部。
以上这些结果在规律上都与工程经验和实际情况相符。
为了进一步验证HSS模型数值模拟结果的可靠性,将HSS模型和现场监测结果进行对比,如图4、5所示,得到以下规律:

图4 HSS模型数值模拟和现场监测获得的地面变形
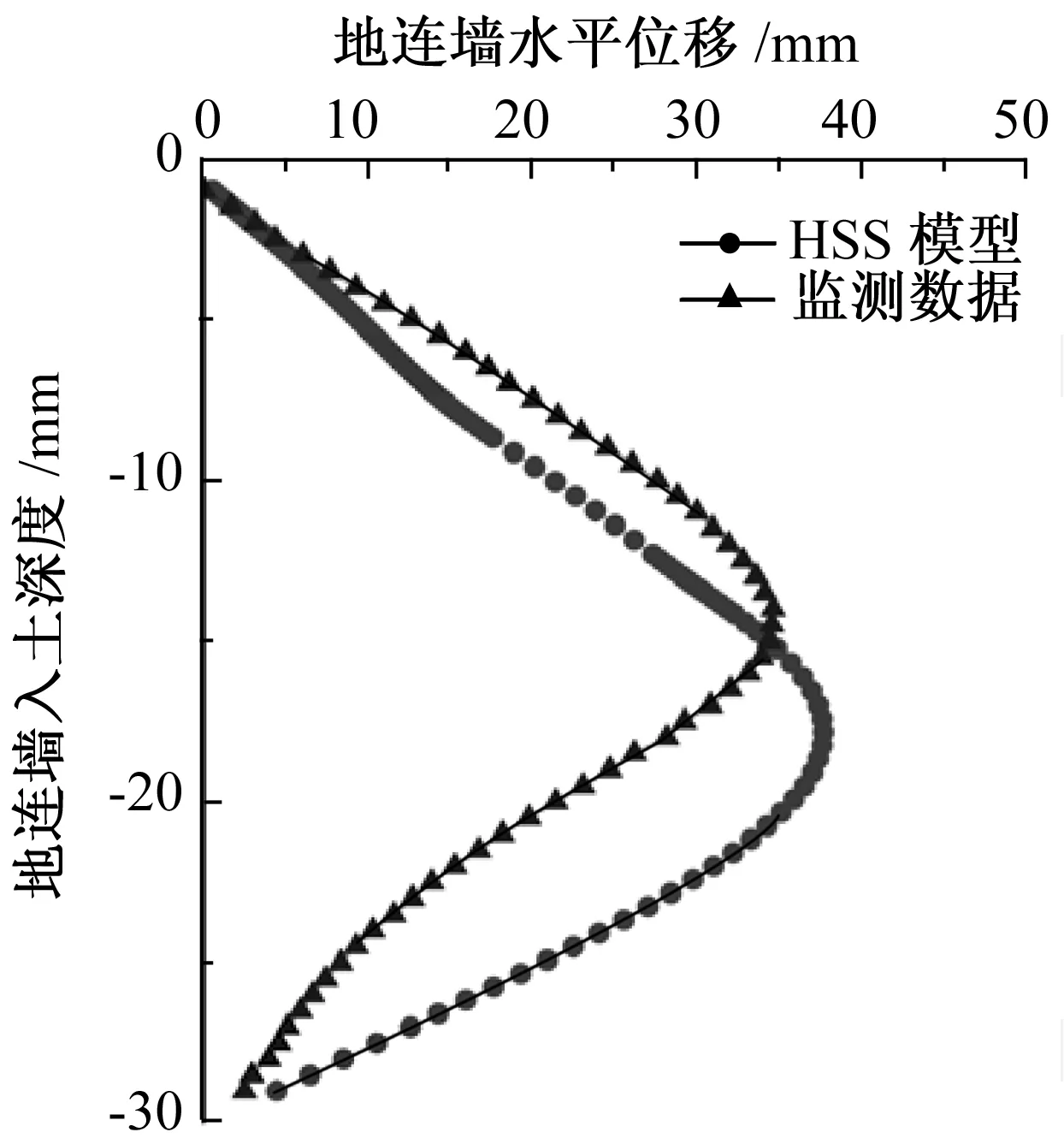
图5 HSS模型数值模拟和现场监测获得的地连墙水平变形
1)HSS模型结果在规律性上与现场监测结果较为一致,地连墙水平变形和地表变形与现场监测的差值在合理范围内,数据吻合度较好。
2)HSS模型能够合理地预测基坑开挖变形特性。但需要指出的是:与现场监测值相比,HSS模型获得的地连墙水平位移最大值位于基坑底部偏下位置,推测是试验获得的HSS参数偏小,使得坑底以下土层比实际偏“软”。
3 基坑突涌判别
建筑基坑规范给出的压力平衡法假定承压水头压力只要不大于含水层顶板不透水层土体自重力,就不会发生突涌。压力平衡法可用如下公式表示:
(1)
式中:γm为透水层以上土的饱和重度;t+Δt为透水层顶面距离基坑底面的深度;Pw为含水层水压力;k为安全系数,一般取1.1。
有限元数值模拟方法考虑了隔水层土体抗剪强度对抗突涌稳定性的有利影响,判别方法比压力平衡法更符合实际,也更为合理。数值模拟和压力平衡法基坑突涌判定结果见表2。压力平衡法基坑突涌判定结果显示,当承压水埋深大于8.8 m(即降水深度超过4.8 m)时,基坑才不会突涌。与传统压力平衡法相比,数值模拟方法显示只有当承压水埋深小于6 m时,基坑才会突涌,所需的降水深度更小。基坑发生突涌时数值计算的结果不收敛,此时隔水层表面土体在承压水作用下产生了拉应力,超过了土体抗剪强度,发生了剪切破坏,基坑底部土体隆起过大。以上分析结果说明传统的基坑突涌压力平衡判别法过于保守,基坑突涌判定应考虑土体抗剪强度的影响。

表2 数值模拟和压力平衡法基坑突涌判定
4 结论
1)由土体HSS模型计算得到的地连墙水平变形和地表沉降与现场监测值较为吻合,差值在合理的范围内,规律性也符合现场实际和工程经验。因此,利用HSS模型预测深基坑开挖对围护结构及周围土体变形是可行的。
2)与传统压力平衡法相比,有限元数值模拟判定基坑突涌需要的降水深度更小,说明传统压力平衡法判定基坑突涌过于保守。基坑突涌判定应考虑土体抗剪强度的影响。
3)准确的土体HSS模型参数是数值模拟结果是否合理的关键。常规岩土工程勘察报告一般没有三轴固结排水卸载-再加载、共振柱试验,研究HSS模型参数与常规岩土工程勘察报告中参数的经验比值,是后续研究的一个重要方向。
