基于GA-ELM的城市轨道交通工程投资估算方法研究

张飞涟，梁秀峰

基于GA-ELM的城市轨道交通工程投资估算方法研究

张飞涟，梁秀峰

(中南大学 土木工程学院，湖南 长沙 410075)

针对影响城市轨道交通工程投资非线性估算性能的特征指标和估算算法2个关键因素，提出优化与改进。对现有城市轨道交通工程投资估算研究成果中14个特征指标，提出优化假设，采用支持向量机(SVM)对样本数据进行训练和估算，通过对比优化前后估算结果的RMSE值进行优化假设验证，最终得到8个特征指标。对城市轨道交通工程投资估算算法，提出遗传算法(GA)优化极限学习机(ELM)输入权值和隐含层阈值的算法，对样本数据进行训练和验证，估算结果RMSE值显示新算法估算精度和稳定性较现有估算算法大幅提高；将提出的城市轨道交通工程投资估算模型与SVM，LSSVM和BP神经网络估算模型相比，估算结果显示本文提出的估算模型比其他估算模型精确度较高。

轨道交通；投资估算；极限学习机；遗传算法；特征指标

传统轨道交通工程投资主要是采用估算指标和概预算定额乘以一定调整系数估算，或根据已完工的类似工程造价数据，建立线性分析模型，如一元、多元回归和比例估算等方法估算。由于定额的滞后性、静态性以及线性函数关系的简单性，不能很好拟合各工程要素与造价之间高度非线性的要求，因此准确性得不到保障。针对这种情况，许多学者对非线性投资测算方法进行了研究。段晓晨等[1]针对有着大量时序数据和非时序数据的新建高铁工程项目，采用混沌时序分析和神经网络分析来估算项目造价；任宏等[2]同样采用神经网络法对建筑工程造价进行估算；严静等[3−4]采用不同的方法改进灰色预测模型对企业成本进行预测。理论上这些方法都需要大量的历史数据才能进行相对准确的预测估算。马国丰等[5]采用神经网络对样本较少的地铁车站工程造价进行估算，估算结果显示也相对较准确。但还需要做进一步的验证。陈进杰[6]采用支持向量机(SVM)的方法对石家庄城市轨道交通1号线的建设成本进行估算。该方法适用于小样本数据的预测估算，但预测结果与实际情况相比如何还有待检验。陈进杰[7]还采用模糊聚类的方法对城市轨道交通运营成本进行了估算，为小样本数据估算提供了新思路新方法，但同样估算结果有待实际检验。杨文成等[8]采用知识约减法对轨道交通成本指标约减，然后用SVM进行成本的估算，提高了计算效率。除此之外还有神经网络与其他算法结合的对工程造价成本估算的方法，如粒子群算法[9]、遗传算法[10]、灰关联[11]等。以上这些测算方法的基本原理都是通过输入特征指标数据，采用一定的智能算法，对工程投资或造价进行非线性估算。估算结果准确与否的两大关键因素是特征指标及估算模型的选取是否科学合理。针对城市轨道交通工程投资估算，本文拟SVM对特征指标进行优化，然后拟寻找一种新的方法对城市轨道交通工程进行投资估算。极限学习机(ELM)是一种泛化性能好、学习速度快的高效预测方法。目前已被应用到浆体流速预测[12]，压铸件晶粒尺寸预测[13]，煤矿爆破预测[14]等领域，均取得了较好的预测结果，但尚未应用到城市轨道交通工程成本估算中。虽然ELM在大部分情况下估算预测能力较好，但输入权值和隐含层阈值是随机给定的，对ELM的稳定性及精度方面都存在很大影响，因此本研究拟选用遗传算法(GA)对ELM参数优化。在轨道交通工程投资估算领域提出GA-ELM预测算法，结合SVM优化的特征指标，以期提高城市轨道交通工程投资估算的精确性。

1 城市轨道交通工程投资估算特征指标优化

目前针对城市轨道交通工程投资估算的特征指标研究较少，陈进杰[6]对城市轨道交通工程投资估算时，采用较宏观的特征指标，指标个数14个；赵欣[15]采用较微观的特征指标，指标个数23个。现有特征指标共同特点是指标数量较多。因此本文拟在现有学者研究的基础上，对特征指标进行筛减优化。由于轨道交通工程投资估算需要历史工程投资数据为基础，再对拟实施的轨道交通工程投资进行估算，如果特征指标较细、较微观，则样本数据就很难收集。因此本文以文献[6]中14个特征指标：通车年份、人均国内生产总值、总里程、地下线长度、地上线长度、地下线比率、地上线比率、车站总数量、地下线车站个数、地上线车站个数、地下线车站比率、地上线车站比率、车辆数量、平均站距为基础，对这些指标进行优化。以优化后的特征指标作为城市轨道交通工程投资估算的特征指标。

1.1 特征指标优化步骤

由于城市轨道交通工程特征指标的优劣无法直接评价，而特征指标的优劣是影响估算优劣的重要原因之一，因此采用估算结果的RMSE(均方根误差)值评估指标的优劣[16]。对特征指标优化，首先在已有指标基础上提出优化假设，再对这些优化假设进行验证，得出最终的特征指标。

特征指标优化步骤如下：

1) 提出特征指标优化假设；

2) 运用目前城市轨道交通工程投资估算的SVM模型，选取训练样本和测试样本，采用原特征指标对预测样本进行估算，估算结果与实际值对比，计算RMSE值，并记录；

3) 将提出的优化特征指标带入测算模型，计RMSE值，与原始RMSE值对比。如果RMSE值变小则假设正确，则用优化后指标代替原指标；否则保留原指标；

4) 通过对所有优化假设验证后，得出城市轨道交通工程投资估算特征指标。

1.2 特征指标优化

1.2.1 提出优化假设

根据特征指标选取的系统性、独立性以及可操作性等原则，对文献[6]中14个特征指标提出以下假设：剔除总里程、敷设方式比率(地下线比率、地上线比率)、车站总数量、车站比率(地下线车站比率、地上线车站比率)、平均站间距。由于这些特征指标为非独立变量，可由其他指标求得，因此剔除。

将剩余的7个特征指标向城市轨道交通设计院的投资测算专家调研咨询，专家们提出：可增加编组这一特征指标。因为编组大小直接决定了拟建车站规模大小。我国城市轨道交通的车型有A，B，C和L型，A型车体型最大，B和C型车体型次之且较相似，L型车体型最小。常见的车编组的形式有4A，4B，4C，4L，6A，6B，6C，6L，8A和8B节编组。为对编组进行量化，按照体型相对大小对编组进行赋值：4A=4，4B=3，4C=2，4L=1，6A=8，6B=7，6C=6，6L=5，8A=10和8B=9。

1.2.2 优化假设验证

本文采用文献[6]中22个样本数据(原文献中有25条城市轨道交通数据，剔除其中的3条轻轨数据)，同时在设计院调研过程中收集了16条城市轨道交通工程投资数据，见表1。总样本数个数为 38个。

表1 设计院收集的样本数据

选取总样本的前85%(32个)为训练样本，其余为测试样本，采用SVM模型对上述城市轨道交通特征优化假设进行验证，验证指标采用RMSE值。首先计算原14个指标的RMSE值，然后分别对各个假设进行计算验证，对比优化后与原指标的RMSE值。计算验证结果见表2所示。

1.2.3 城市轨道交通工程投资估算特征指标

通过对上述优化假设的验证后，在原来14个特征指标的基础上剔除了总里程、地上地下线比例(地下线比率、地上线比率)、车站总数、车站比例(地下线车站比率、地上线车站比率)。优化后的城市轨道交通工程投资估算特征指标见图1所示。

表2 特征指标优化计算验证结果

图1 城市轨道交通工程投资估算特征指标

2 基于遗传算法对极限学习机优化的估算算法

2.1 极限学习机

极限学习机(ELM)是一种针对单隐含层前馈神经网络(SLFN)的新算法[17]，ELM的输入权值和隐含层阈值是随机给定的，只需设置隐含层节点个数就可产生唯一最优解。可通过求解线性方程组的最小二乘解获得输出权值。

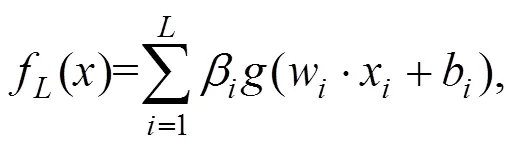
当训练样本个数与隐含层神经元个数相等时，则存在，和使：

式( 2)可写作：

在ELM算法中，和可随机给定，则变为一个确定的矩阵，被称作网络的隐含层输出矩阵。输出权值矩阵可求解式(4)得到。

其中：+为隐含层输出矩阵的广义逆。

2.2 遗传算法原理

虽然ELM在大部分情况下估算预测能力较好，但和是随机给定的，对ELM的稳定性及精度方面都存在很大影响，在实际的应用过程中经常出现病态[18]或过拟合现象。因此本文提出采用遗传算法(GA)对ELM中的和进行寻优，优化ELM，提高其估算的精确性。

遗传算法基本原理是将问题的解转化为染色体，通过选择、交叉及变异等变换染色体中的信息，最终遗传进化到符合目标的染色体。

2.3 GA-ELM优化的估算算法流程

根据上述理论，基于GA优化ELM(GA-ELM)的城市轨道交通工程投资估算步骤如下。

Step 1：载入样本数据，随机选取样本数据的85%，作为训练集，其余作为测试集，对样本数据归一化处理。

Step 2：随机生成ELM的输入权值和隐含层阈值，并对其进行二进制编码，作为GA的初始种群。

Step 3：计算GA目标函数，即RMSE值。将和解码，将其赋予给ELM，使用训练样本对网络进行训练，然后采用训练好的网络对预测样本进行估算，并与测试样本实际输出值计算RMSE值，得到GA目标函数。

Step 4：通过GA的选择、交叉、变异得到新群体，即遗传变异后的和，达到遗传代数后终止遗传，得到最终的群体。

Step 5：对迭代遗传后的最终群体解码，得到最优和。

Step 6：将最优和赋予ELM。

Step 7：采用最优的和，使用训练样本对ELM网络进行训练，训练结束后得到城市轨道交通工程投资估算模型。

3 实例分析

3.1 样本选取及参数设置

样本数据同样采用1.2中数据，随机选取85%(32个)作为训练样本，其余作为测试样本。城市轨道交通投资特征指标选取本文优化后的8个特征指标。

ELM隐含层节点数设置为32[19]。遗传算法参数设置为：种群大小40，遗传代数100，染色体长度10，交叉概率0.7，变异概率0.01和代沟0.95。

3.2 测试分析

载入样本数据，随机选择训练样本，通过GA优化ELM的和，将其带入到ELM模型中，训练网络模型，对测试样本进行估算。为验证本文提出的估算算法性能的优越性，同时采用SVM算法对轨道交通测试样本进行估测，SVM核函数为RBF，惩罚因子和核函数中的方差采用交叉验证确定。GA-ELM算法与SVM算法估算结果见表3和如图2。

从图2可直观看出GA-ELM算法估算结果与真实值较贴近，而SVM算法估算结果不太理想。通过计算GA-ELM算法与SVM算法估算结果与实际值的RMSE值见表4，定量评价两种估算算法的优劣。GA-ELM算法估算结果RMSE值为12.562，SVM算法为28.898。与SVM估算算法相比，GA-ELM算法估算结果的RMSE降低56.5%，预测准确性大幅提高。由于GA-ELM采用遗传算法优化参数，因此其训练样本时间相对SVM算法较长，预测效率较低，还有提升空间。

表3 GA-ELM算法与SVM算法估算结果

图2 GA-ELM算法与SVM算法预测结果图

表4 GA-ELM与SVM算法估算结果RMSE值

同时为对比GA-ELM算法与SVM算法估算的稳定性，随机选取训练样本和测试样本10次，使用优化后的8个特征指标，分别采用SVM和GA-ELM算法估算，计算每次估算结果的RMSE值，计算结果见表5。然后计算SVM和GA-ELM算法估算结果RMSE值的平均值和标准差，通过标准差反映估算结果离散程度，来验证2种算法的稳定性。从计算结果可以看出SVM估算结果RMSE值的平均值和标准差较大，其估算的准确性和稳定性较差，而GA-ELM算法估算结果的RMSE值的平均值和标准差较小，其估算的准确性和稳定性较好。

表5 随机10次估算结果RMSE值及其均值和标准差

将优化后的特征指标及算法的估算模型与现有估算模型对比，随机选取85%(32个)作为训练样本，其余15%(6个)作为测试样本。计算结果见表6。从表6可看出不同模型使用优化后的指标，较使用原指标估算精度大大提高，同时也可看本文优化后的8个特征指标的GA-ELM估算模型，比现有14个特征指标的SVM模型估算精度大大提高。

表6 城市轨道交通工程投资GA-ELM估算模型与SVM估算模型对比

本文提出的城市轨道交通工程投资GA-ELM估算模型比现有SVM模型预测准确和稳定的原因在于剔除了多余或干扰的特征指标，且采用更为先进的GA-ELM算法。

为进一步对比分析城市轨道交通工程投资GA- ELM估算模型性能，分别采用SVM、GA-ELM、最小二乘支持向量机(LSSVM)、BP神经网络估算模型对城市轨道交通工程投资进行估算对比。同样随机选取85%(32个)样本作为训练样本，其余作为测试样本，对测试样本进行投资估算，其计算结果对比见图3。

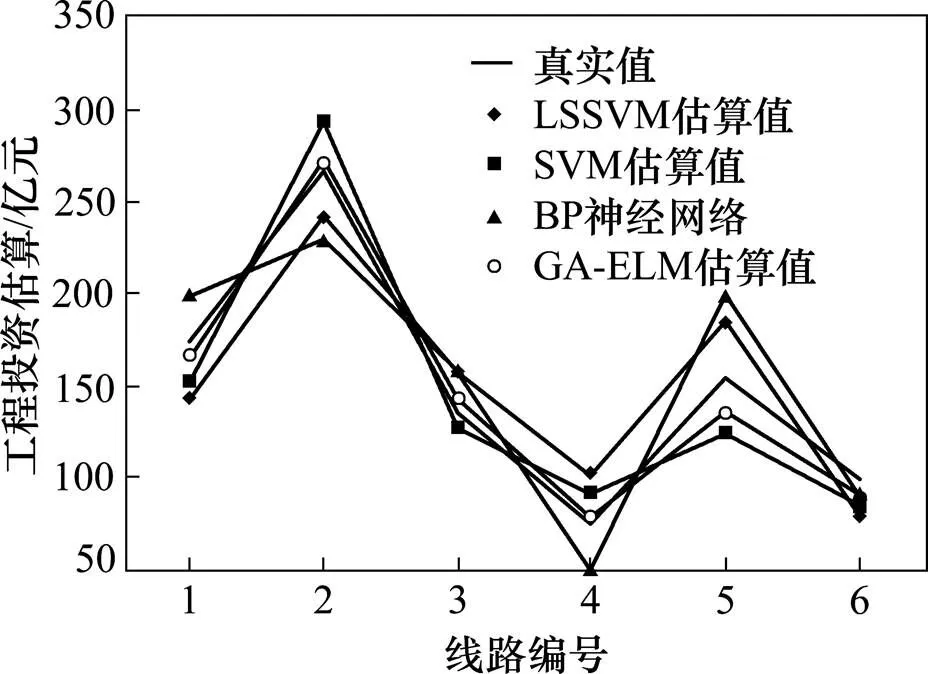
图3 各种估算模型估算结果对比图

从图3可看出，GA-ELM估算模型计算结果曲线与实际值曲线拟合度及贴近度最好；其次为SVM估算模型，再次为LSSVM估算模型，最后为BP神经网络估算模型。这进一步验证了本文提出的投资估算模型比其他估算模型有较好的性能。

4 结论

1) 在现有城市轨道交通工程投资估算14个特征指标基础上，通过提出特征指标优化假设及验证，最后优化得到8个特征指标。特征指标优化后减少了输入数据，同时提高了估算精度。

2) 针对估算算法，提出了采用GA优化ELM输入权重和隐含层阈值的估算算法，通过与已有的轨道交通工程投资估算算法估算结果相比，准确性和稳定性有显著提高。

3) 优化和提出的城市轨道交通工程投资估算模型与SVM，LSSVM和BP神经网络估算模型相比，估算结果有较高的精度。

[1] 段晓晨, 郭兰英, 张新宁. 新建高铁工程非线性造价估算方法研究[J]. 铁道学报, 2013, 35(10): 114−122. DUAN Xiaochen, GUO Lanying, ZHANG Xinning. Research on nonlinear estimating methods of whole life-cycle cost for china high-speed railway prohect[J]. Journal of the China Railway Society, 2013, 35(10): 114−122.

[2] 任宏, 周其明. 神经网络在工程造价和主要工程量快速估算中的应用研究[J]. 土木工程学报, 2005, 38(8): 135−138. REN Hong, ZHOU Qiming. Applicaion of neural network for quick estimation of engineering constructon cost and main quantities[J]. China Civil Engineering Journal, 2005, 38(8): 135−138.

[3] 严静. 基于改进灰色预测的成本预测模型构建[J]. 统计与决策, 2014(3): 39−41. YAN Jing. Construction of cost prediction model based on improved grey prediction[J]. Statistics and Decision, 2014(3): 39−41.

[4] 王惠珍. 基于改进灰色系统GM(1,1)模型的成本预测[J]. 统计与决策, 2015(15): 83−86. WANG Huizhen. Cost prediction based on improved gray system GM(1,1) model[J]. Statistics and Decision, 2015(15): 83−86.

[5] 马国丰, 陈志琴. 基于BP神经网络的轨道交通车站工程项目估价研究[J]. 项目管理技术, 2011, 9(7): 55−60. MA Guofeng, CHEN Zhiqin. Research on evaluation of rail transit station engineering project based on BP neural network[J]. Project Management Technology, 2011, 9(7): 55−60.

[6] 陈进杰. 城市轨道交通项目广义全寿命周期成本理论与应用研究[D]. 北京: 北京交通大学, 2011. CHEN Jinjie. Theory and application of generalized life cycle cost of urban rail transit project[D]. Beijing: Beijing Jiaotong University, 2011.

[7] 陈进杰, 王兴举, 高桂凤. 城市轨道交通运营成本模糊聚类估算模型[J]. 交通运输系统工程与信息, 2011, 11(2): 136−141. CHEN Jinjie, WANG Xingju, GAO Guifeng. Estimation model for operating costs of urban rail transit based on fuzzy clustering[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(2): 136−141.

[8] 杨文成, 王圆圆, 孙军先. 基于 KR-SVM 的城市轨道交通建设成本估算评价模型研究[J]. 交通工程, 2017, 17(3): 40−46. YANG Wencheng, WANG Yuanyuan, SUN Junxian. The research on evaluation model of urban rail transit construction cost based on KR-SVM[J]. Journal of Transportation Engineering, 2017, 17(3): 40−46.

[9] 陈伟, 周曼, 叶家军, 等. 建筑工程安全施工费费率测算的PSO-BP模型研究[J]. 中国安全科学学报, 2016, 26(5): 146−151. CHEN Wei, ZHOU Man, YE Jiajun, et al. PSO-BP modeling research on fee rate measurement of construction project safe construction cost[J]. China Safety Science Journal, 2016, 26(5): 146−151.

[10] 景晨光, 段晓晨. 基于遗传神经网络的工程造价估算方法研究[J]. 石家庄铁道大学学报(社会科学版), 2010, 4(4): 11−17. JING Chenguang, DUAN Xiaochen. Research on model of engineering cost estimation based on genetic neural network[J]. Journal of Shijiazhuang Tiedao University (Social Science), 2010, 4(4): 11−17.

[11] 杨永明, 王燕, 范秀君, 等. 基于灰关联−神经网络的电力工程造价估算[J]. 重庆大学学报, 2013, 36(11): 15−20. YANG Yongming, WANG Yan, FAN Xiujun, et al. Cost estimate of power line projects based on grey relational analysis and neural networks[J]. Journal of Chongqing University, 2013, 36(11): 15−20.

[12] 王新民, 李天正, 张钦礼. 基于 GA-ELM 浆体管道输送临界流速预测模型研究[J]. 中国安全生产科学技术, 2015, 11(8): 101−105. WANG Xinmin, LI Tianzheng, ZHANG Qinli. Study on prediction model of critical flow velocity in slurry pipeline transportation based on GA-ELM[J]. Journal of Safety Science and Technology, 2015, 11(8): 101−105.

[13] 梅益, 孙全龙, 喻丽华, 等. 基于GA-ELM 的铝合金压铸件晶粒尺寸预测[J]. 金属学报, 2017, 53(9): 1125−1132. MEI Yi, SUN Quanlong, YU Lihua, et al. Grain size prediction of aluminum alloy dies castings based on GA-ELM[J]. Acta Metallurgica Sinica, 2017, 53(9): 1125−1132.

[14] 温廷新, 陈晓宇, 邵良杉, 等. 参数优化 GA-ELM 模型在露天煤矿抛掷爆破的预测[J]. 煤炭学报, 2017, 42(3): 630−638. WEN Tingxin, CHEN Xiaoyu, SHAO Liangshan, et al. Prediction on parameters optimized GA-ELM model for cast blasting in open-pit mine[J]. Journal of China Coal Society, 2017, 42(3): 630−638.

[15] 赵欣. 基于BP神经网络的地铁土建工程造价估算方法研究[D]. 北京: 北京交通大学, 2008. ZHAO Xin. Resarch on civil engineering cost estimation method of subway based on BPNN[D]. Beijing: Beijing Jiaotong University, 2008.

[16] 张颖, 李梅. 基于粒子群优化极限学习机的水质评价新模型[J]. 环境科学与技术, 2016, 39(5): 135−139. ZHANG Ying, LI Mei. A novel evaluation model of water quality based on PSO-ELM method[J]. Environmental Science & Technology, 2016, 39(5): 135− 139.

[17] HUANG G B, ZHU Q Y, Siew C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1): 489−501.

[18] TANG X, HAN M. Partial Lanczos extreme learning machine for single-output regression problems[J]. Neurocomputing, 2009, 72(13−15): 3066−3076.

[19] 史峰, 王辉, 郁磊, 等. MATLAB 智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011. SHI Feng, WANG Hui, YU Lei, et al. 30 Case analysis of MATLAB intelligent algorithm[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2011.

Research on investment estimation method of urban rail transit project based on GA-ELM

ZHANG Feilian, LIANG Xiufeng

(School of Civil Engineering, Central South University, Changsha 410075, China)

According to two key factors affecting the nonlinear estimation performance of urban rail transit engineering investment, the optimization and improvement were proposed. Based on the 14 characteristics of the existing urban rail transit engineering investment estimation results, the optimization hypothesis was proposed. The support vector machine (SVM) was used to train and estimate the sample data. The RMSE value of the estimation results before and after the optimization was compared to optimize the hypothesis verification. Eight characteristic indicators were obtained. For the urban rail transit engineering investment estimation algorithm, the algorithm of genetic algorithm (GA) optimization limit learning machine (ELM) input weight and hidden layer threshold was proposed. The sample data was trained and verified. The estimated result RMSE value reveals that the estimation accuracy and stability of the new algorithm are significantly improved compared with the existing estimation algorithms. Finally, the proposed urban rail transit engineering investment estimation model was compared with the SVM, LSSVM and BP neural network estimation models. The estimation results show that the proposed estimation model is better than the other. The estimation model is more accurate.

rail transit; investment estimation; extreme learning machine; genetic algorithm; feature index

U121

A

1672 − 7029(2019)07− 1842 − 07

10.19713/j.cnki.43−1423/u.2019.07.031

2018−09−20

国家重点研发计划资助项目(2017YFB1201102)

张飞涟(1964−)，女，湖南湘潭人，教授，博士，从事工程项目规划与管理研究；E−mail：zfl@csu.edu.cn

(编辑 蒋学东)