基于机器学习的地铁列车牵引能耗预测研究

吕欢欢，张玉召

基于机器学习的地铁列车牵引能耗预测研究

吕欢欢，张玉召

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

针对城市轨道交通运营管理过程中，准确预测列车牵引能耗有利于合理编制运营组织模式和评价用能效率。针对影响列车牵引能耗的因素繁多，传统的数学回归方法难以保证预测效果的问题，提出基于机器学习的牵引能耗预测方法，运用支持向量回归(SVR)和随机森林回归(RFR)2种机器学习方法建立列车牵引能耗预测模型。选取影响能耗的6种可变因素，分别从单个可变因素和多个可变因素对地铁能耗的影响进行分析；遍历寻求最优参数组合；利用RFR模型对地铁牵引能耗的影响因素进行重要度的排序，使影响因素的重要度得以量化描述；以北京地铁昌平线真实运行能耗数据为例进行验证，研究结果表明：SVR与RFR都表现稳定并能达到较高的预测精度。

城市轨道交通；牵引能耗预测；支持向量回归；随机森林回归；能耗影响因素

地铁作为城市的重要公共交通之一，由于其速度快、运量大、占地少等优点在各大城市得到快速发展。现阶段城市地铁网络加速扩展，其能耗也随之攀升。地铁能耗的主要构成有车站设施设备运营能耗和列车运行能耗，其中列车运行过程中的牵引能耗占地铁总能耗的一半以上。据统计，北京市地铁用电量从2010年至2017年一直呈上升趋势，其中列车牵引能耗电量占总能耗电量一半以上[1]，如图1所示。因此，地铁牵引能耗预测这一研究备受关注。精准、快速的预测地铁牵引能耗有利于合理设置线路条件、编制运输组织模式，提高设备利用率，降低运营成本[2]。

图1 北京地铁2010~2017年牵引耗电量趋势

地铁牵引能耗量大，涉及影响因素众多，国内外众多学者从不同角度、利用不同方法对能耗预测或节能运行方面做了广泛深入的研究，以提出更好的节能策略。Scheepmaker等[3−7]结合时刻表研究列车节能控制方法或建立节能优化模型，提出优化能源使用的决策或地铁运营管理的节能方案。陈垚等[8]从列车属性角度出发，通过分析不同列车属性对牵引能耗的影响程度，得出不同列车在不同线路节能的适用性。宋文婷等[9−11]通过分析列车牵引特性、线路运行条件建立节能模型，综合考虑了再生制动储能及线路运行等条件，提出优化速度曲线、机车操纵或新的调度方法，并得到了预期的节能效果。杨臻明等[12−13]通过分析历史数据构建多元线性回归模型进行能耗预测从而提出优化运营调度、评价用能的依据。上述文献对地铁能耗预测研究和地铁节能方面的研究，主要通过建立能耗解析模型、运用仿真验证或分析历史数据建立回归模型等一些方法展开研究。然而，地铁牵引能耗过程复杂、实际运行线路情况多变，影响牵引能耗的因素繁多且能耗与各因素之间呈非线性关系，采用以上方法可能会出现预测结果不够精确或预测角度过于局限等问题。为充分考虑列车牵引能耗的影响因素，更精准地预测地铁牵引能耗量，本文采用支持向量回归(SVR)和随机森林回归(RFR)2种机器学习方法对地铁能耗展开预测。这2种方法可以有效解决高维度、非线性条件下的数据问题，对数据集的适用范围广泛，数据集表现良好，不易出现过拟合现象，具有良好的准确率。并且，利用RFR可以对所选地铁牵引能耗的影响因素进行重要度的排序，使影响因素的重要度得以量化，为运营组织工作的安排提供有力依据。

1 研究方法介绍

1.1 支持向量回归(SVR)

支持向量回归(SVR)是以统计学为理论框架下的机器学习方法[14]。SVR的本质是求解凸二次规划问题，其核心思想可以总结为以下几点：

1) SVR是专门针对有限样本情况的，其目标是得到现有数据下的最优解而不仅仅是样本数趋于无穷大时的最优解；

2) SVR解决的是凸二次规划问题，本质上来讲得到的是全局最优解；

3) SVR将实际非线性问题转化成高维度的特征空间，维数问题得以解决，具有较广的适用范围。

支持向量回归机的算法步骤归纳为：

1) 给定训练集

2) 选取适当的核函数(,′)以及适当的精度>0和惩罚参数>0；

3) 构造并求解凸二次规划问题

得解：

5) 构造决策函数

1.2 随机森林回归(RFR)

随机森林回归(RFR)也是一种统计学理论机器学习方法。其最大优势在于它既可用于回归又可用于分类，易得每个特征对预测的相对重要性[15]。随机森林的本质是通过创建随机的决策树，并使用这些决策树构建较小的树，随后组成多决策树模型，本方法可以防止多数情况下的过拟合。RFR算法步骤归纳如下。

1) 设随机参数向量为，采用bootstrap方法重采样，产生个随机训练集1，2，…，θ；从而生成对应的个决策树{(,1)，(,2)}，…，{(, θ)}；

2) 从维特征中选取个特征做当前节点的分裂特征集，并以最好的分列方式对节点分裂；

3) 使每个决策树最大限度生长，不进行剪枝；

4) 假使一个新数据=，令权重向量为：ω(,)；

5) 由给定的自变量=，得出单棵决策树的预测值；

6) 由决策树权重ω(,)取平均，得到每个观测值的权重ω()，对所有单棵决策树的观测值得到随机森林预测。

2 数据准备

2.1 选取数据

地铁牵引能耗即地铁列车在运行过程中所消耗的电能。地铁牵引能耗影响因素的分类及其可变因素如表1所示[16]。

表1 地铁牵引能耗影响因素的分类及其可变因素

本文研究将提取影响牵引能耗的6种主要可变因素展开预测，提取的影响因素分别是：运行时间，最大速度(与列车速度控制点有关)，平均接触网压，运行里程，变化坡度值(与坡度转换点有关)，列车重量(影响势能变化)。

所用到的数据来源于实际的北京地铁昌平线真实实验测试数据，具体为包括精确到0.2 s的地铁的实时速度，实时运行距离，实时接触网电压，区间的限速，区间的坡度变化，采用的车辆类型，车辆的重量等，最后是具体到每个区间运行消耗的实际牵引能耗。

2.2 数据分析

北京地铁昌平线共包含12个站点，11个区间，测试数据包含3个月内接近1 000次区间的记录数据，如图2所示为其中西二旗至生命科学园区间列车运行情况。每个区间的记录数在500~1 500左右，区间测试数据包含的部分信息如表2所示，每个区间的能耗汇总统计以下行方向为例，如表3所示。

提取列车在每个区间的运行时间、运行距离、最大速度和坡度变化值，对列车重量、区间供电网压提取平均值，并对应每个区间的能耗如表4所示。其中，坡度变化值的计算方法：

则整个区间的坡度变化值为：

式(7)中：SC代表区间的坡度改变值；i代表区间的运行时间。

图2 区间测试数据包含的部分信息

表2 原始数据中某一区间的数据信息(部分)

表3 昌平线某日测试的运行时间与能耗数据

表4 提取变量的数据信息(部分)

为了挖掘各种影响因素与牵引能耗的关系，本文从单个因素，多个因素与牵引能耗关系的角度出发，分别进行分析。

首先，对单个影响因素与牵引能耗关系趋势进行分析，各分析结果如图3~5所示。

1) 列车运行时间与牵引能耗的变化趋势散点图如图3所示。

图3 运行时间-能耗关系变化图

牵引能耗随着列车运行时间呈周期性变化，在周期范围内随着时间的增加能耗随之下降。

2) 运行距离与牵引能耗的变化趋势图如图4所示。

牵引能耗随着运行距离呈周期性变化，在周期范围内随着运行距离的增加能耗随之增加。

3) 坡度变化值与能耗的折线图如图5所示。

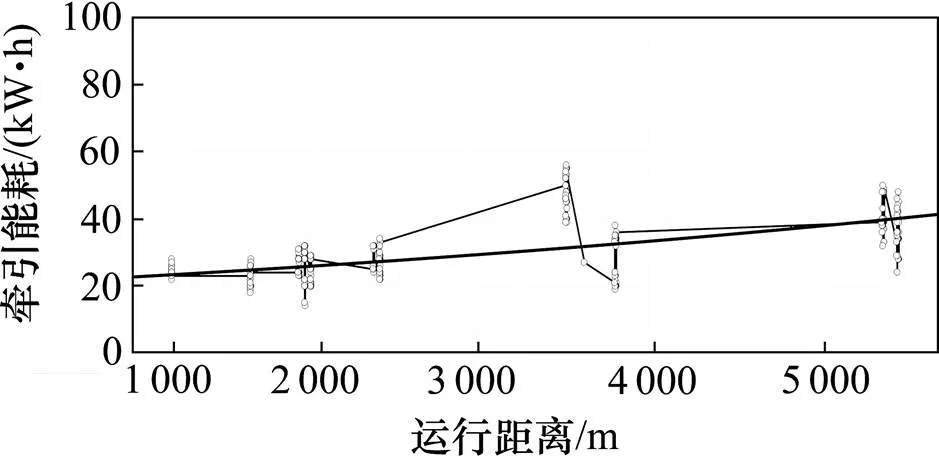
图4 运行距离-能耗关系变化图

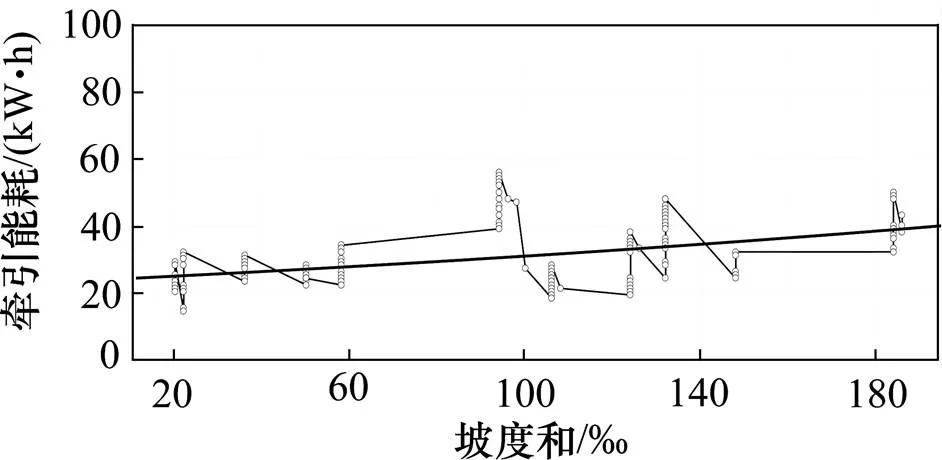
图5 坡度变化值-能耗关系变化图

牵引能耗随着坡度值变化呈周期性变化，在周期范围内随着坡度变换值的增加，能耗随之增加。另外，列车运行最大速度、列车质量、平均网压与能耗的关系变化趋势在周期范围内随着自身量的增加能耗也随之增加。

其次，对多个影响因素与牵引能耗关系趋势进行分析，各分析图示如图6和7所示。得出地铁牵引能耗与任意2个影响因素之间的关系复杂程度，由此可知能耗与众多因素之间关系的复杂性，因此，本文充分考虑影响地铁牵引能耗的主要可变因素，将其作为SVR和RFR的输入，对列车牵引能耗进行预测。

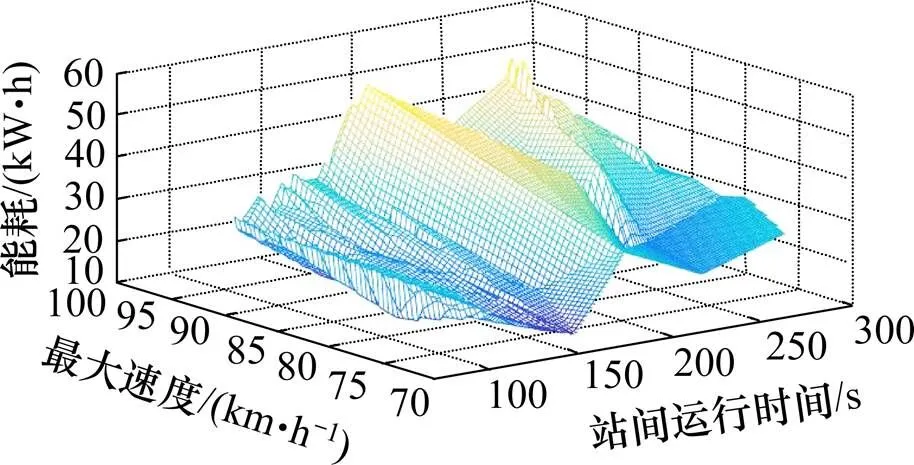
图6 运行时间-最大速度-能耗关系图

图7 最大速度-运行距离-能耗关系图

3 预测过程及结果分析

3.1 支持向量回归(SVR)预测过程及结果

将现有数据随机采样，数据总量的80%作为训练，20%作为测试，并将训练数据和测试数据进行标准化处理，以便消除不同因素之间的数量级的影响，接着利用交叉检验测试标定模型参数。

利用支持向量回归预测时需要标定2个参数，即核函数，以及惩罚参数。核函数选择综合表现稳定的径向基(RBF)核函数用于测试集进行测试，利用决策系数2进行评价模型的泛化精度，训练过程如图8所示。由图中可以看出，当惩罚参数增大到20左右时，决策系数2增大到最大值，并保持稳定，所以惩罚参数取20，核函数参数取径向基函数(=1)。最后，用于测试的样本实际值与预测值的比较如图9所示，部分预测值与实际值对比数据如表5所示，由图9和表5所示预测结果表明，在最优参数条件下，能耗预测的平均误差在2.1 kW∙h左右收敛，SVR的预测精度达到96%(平均能耗46 kW∙h，1-2.1/46*100%=96%)。

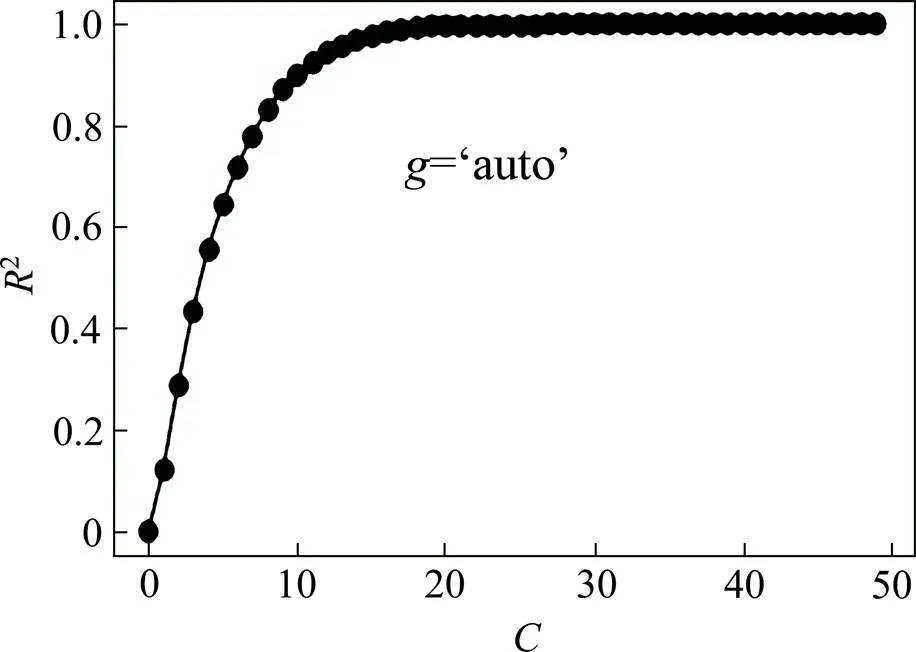
图8 决策系数R2与惩罚参数C的变化过程

图9 SVR的预测值与实际值比较图

3.2 随机森林回归(RFR)预测过程及结果

首先将提取的数据总量的80%作为训练集，数据总量的20%作为测试集，并进行交叉检验测试标定参数，提高生成模型的泛化精度。其中参数标定过程：在随机森林回归算法中，需要标定3个重要的参数:决策树数目(ntree)，分裂属性个数(mtry)，叶节点最小样本数(min sample leaf)。

表5 RFR实际值与预测值的对比(部分)

为验证随机森林回归算法的收敛性，将决策树数目设置为0~1 000，其收敛过程如图10所示，可知所测试的平均误差是逐渐收敛的。同样，从0~10遍历分裂属性个数，如图11所示，所测试的平均误差也是收敛的。由于0~1 000棵数的遍历时间较长，并且当决策树数目为100左右时误差已经收敛，进如图12所示测试100 组样本，发现平均误差收敛在2.3 kW∙h附近。

图10 决策树数目的收敛过程

为使预测精度达到最优，需要标定最优的参数组合，采取的方法是枚举遍历的方法。通过枚举，mtry:1-10的收敛情况，发现不同分裂属性个数mtry参数，误差都能收敛。为使图示看得清晰，选取收敛情况较好的参数，如图13所示为选取当mtry=1，2和7时的收敛过程，可得最优的mtry=2。同样，遍历不同的叶节点最小样本数，不同的叶节点参数，误差同样能收敛如图14所示为选取当叶节点最小样本数min leaf node=1，2，5和10时的收敛过程，可得最优的min leaf node=2。

图11 不同分裂属性个数组别下的收敛过程

图12 多组测试下平均的收敛过程

图13 不同mtry下的收敛过程

图14 不同叶节点下的收敛过程

用于测试的100个样本的实际与预测值的比较如图15所示，其中部分预测与实际对比数据如表6所示。

图15 RFR的预测值与实际值比较图

表6 RFR实际值与预测值的对比(部分)

由图15和表6所示预测结果表明，遍历得到的在最优参数条件下，能耗预测的平均误差在2.3 kW∙h左右收敛，RFR预测精度达到95%(1-2.3/46* 100%=95%)。

利用选取最优参数下的RFR训练算法对提取的6种因素进行重要度排序，如图16所示，得出影响区间牵引能耗的因素重要度依次为站间距离、站间最大速度、站间运行时间、站间坡度变化值、平均供电网压和车辆质量。

图16 各影响因素的重要度排序

最后，通过实际值与预测值的对比可以发现，大部分预测结果与实际值相差较小，加之实验数据本身存在一些异常值，以及读取的能耗的精度只在整数范围，所以，预测结果已具备较高的预测精度。

4 结论

1) 准确预测城市轨道交通列车牵引能耗，对列车运营能耗评估与节能等有重要意义。影响地铁牵引能耗的因素众多，采用SVR和RFR的2种机器学习方法对地铁能耗进行预测，可以有效处理多因素条件下的非线性关系问题，避免过拟合现象。

2) 利用SVR和RFR 两者都可以有效解决高维度和非线性难题，并较好的预测列车牵引能耗量。通过北京地铁真实运行能耗数据的实例验证，2种预测方法都表现良好,平均误差收敛在2.3 kW∙h左右。当然，2种方法在预测精度和预测高效性具有各自的优势。从预测精度分析，SVR较RFR的预测精度略高，但是，利用RFR可以得出影响牵引能耗因素的重要度排序，这是RFR的一个突出优势。因为量化不同因素的重要程度，有助于运营组织工作过程中，对牵引能耗的节能策略有较好的侧重。

[1] 刘小玲, 薛亮. 城市轨道交通节能问题研究[J]. 资源节约与环保, 2017, 23(1): 45−46. LIU Xiaoling, XUE Liang. Research on energy saving of urban rail transit[J]. Resource Conservation and Environmental Protection, 2017, 23(1): 45−46.

[2] González-Gil A, Palacin R, Batty P. Optimal energy management of urban rail systems: Key performance indicators[J]. Energy Conversion and Management, 2015, 90(1): 282−291.

[3] Scheepmaker Gerben M, Goverde Rob M P, Kroon Leo G. Review of energy-efficient train control and timetabling [J]. European Journal of Operational Research, 2017, 257(2): 355−376.

[4] YANG Songpo, WU Jianjun, YANG Xin, et al. Energy-efficient timetable and speed profile optimization with multi-phase speed limits: Theoretical analysis and application[J]. Applied Mathematical Modelling, 2018, 56(4): 32−50.

[5] 李佳杰, 柏赟, 邱宇, 等. 现代有轨电车时刻表与操纵节能协同优化[J]. 铁道科学与工程学报, 2017, 14(7): 1552−1558. LI Jiajie, BAI Yun, QIU Yu, et al. Coordinated optimization of modern tram control and timetable for energy saving[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1552−1558.

[6] YANG Xin, LI Xiang, NING Bin, et al. A survey on energy-efficient train operation for urban rail transit[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(1): 2−13.

[7] YANG Xin, LI Xiang, GAO Ziyou, et al. A cooperative scheduling model for timetable optimization in subway systems[J]. IEEE Transactions on Intelligent Transporta- tion Systems, 2013, 14(1): 438−447.

[8] 陈垚, 毛保华, 柏赟, 等. 列车属性对城市轨道交通牵引能耗的影响及列车用能效率评价[J]. 中国铁道科学, 2016, 37(2): 99−105. CHEN Yao, MAO Baohua, BAI Yun, et al. Impact of train characteristics on traction energy consumption of urban rail transit and evaluation on train energy efficiency[J]. China Railway Science, 2016, 37(2): 99− 105.

[9] 宋文婷, 谭觅, 蔡文川, 等. 高速列车的节能操纵策略研究[J]. 铁道科学与工程学报, 2016, 13(3): 423−429. SONG Wenting, TAN Mi, CAI Wenchuan, et al. Research on energy-saving operation strategy for high-speed train[J]. Journal of Railway Science and Engineering, 2016, 13(3): 423−429.

[10] 曹佳峰, 刘斌. 基于2阶段优化的高速列车节能运行仿真研究[J]. 铁道科学与工程学报, 2018, 15(4): 821−828. CAO Jiafeng, LIU Bin. Research on simulation for energy-saving operation of high-speed trains based on two-stage optimization[J]. Journal of Railway Science and Engineering, 2018, 15(4): 821−828.

[11] YANG Xin, CHEN Anthony, LI Xing, et al. An energy-efficient scheduling approach to improve the utilization of regenerative energy for metro systems[J]. Transportation Research Part C, 2015, 57(8): 13−29.

[12] 杨臻明, 岳继光, 王晓保, 等. 基于回归模型的城市轨道交通能耗预测[J]. 城市轨道交通研究, 2010, 13(12): 22−25. YANG Zhenming, YUE Jiguang, WANG Xiaobao, et al. Prediction of urban rail transit power consumption based on regression model[J]. Urban Mass Transit, 2010, 13(12): 22−25.

[13] 刘鹏, 田琼. 城市轨道交通列车牵引能耗分析[J]. 山东科学, 2012, 25(3): 7−11. LIU Peng, TIAN Qiong. Analysis of traction energy consumption of urban rail transit[J]. Shandong Science, 2012, 25(3): 7−11.

[14] 陈垚, 毛保华, 柏赟, 等. 基于支持向量回归的地铁牵引能耗预测[J]. 系统工程理论与实践, 2016, 36(8): 2101−2107. CHEN Yao, MAO Baohua, BAI Yun, et al. Forecasting traction energy consumption of metro based on support vector regression[J]. Systems Engineering-Theory & Practice, 2016, 36(8): 2101−2107.

[15] 方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32−38. FANG Kuangnan, WU Jianbin, ZHU Jianping, et al. Review of research on random forest methods[J]. Statistics and Information Forum, 2011, 26(3): 32−37.

[16] González-Gil A, Palacin R, Batty P. A systems approach to reduce urban rail energy consumption[J]. Energy Conversion and Management, 2014, 80(4): 509−524.

Research on the prediction of traction energy-consumption of subway train based on machine learning

LÜ Huanhuan, ZHANG Yuzhao

(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

In the process of urban rail transit operation and management, a precise prediction of train traction energy-consumption is beneficial to the rational establishment of operation organization mode and evaluation of energy efficiency. However, the factors affecting the traction energy-consumption of trains are complex, and the traditional mathematical regression method is difficult to ensure the prediction effect. In this paper, a method for predicting traction energy-consumption based on machine learning was proposed. Two machine learning methods, Support Vector Regression (SVR) and Random Forest Regression (RFR), were utilized to establish the forecasting model of train traction energy-consumption. Firstly, six typical factors were selected. And, influences from both single and multiple factors were analyzed. Then, the optimal parameter combinations were searched with an enumerative method. In addition, the RFR model was utilized to rank the importance of factors influencing traction energy-consumption, so that the importance of the influencing factors can be quantified. Finally, the proposed method was verified by taking the real operation energy-consumption data of Beijing Metro Changping Line as an example. The results show that both SVR and RFR are stable and can achieve high prediction precision.

urban rail transit; traction energy-consumption prediction; support vector regression (SVR); random forest regression (RFR); energy-consumption influencing factor

U29-3

A

1672 − 7029(2019)07− 1833 − 09

10.19713/j.cnki.43−1423/u.2019.07.030

2018−10−10

国家自然科学基金资助项目(71761025)；甘肃省高等学校科研资助项目(2018A-023)

张玉召(1981−)，男，安徽砀山人，副教授，博士，从事轨道交通运输组织与优化、客货运技术与管理研究；E−mail：yuzhaozhang@126.com

(编辑 蒋学东)