基于峭度与互相关的IEWT轴承故障诊断方法研究
2019-03-24郭辉伍川辉刘泽潮黄衍于昊明
郭辉,伍川辉,刘泽潮,黄衍,于昊明
基于峭度与互相关的IEWT轴承故障诊断方法研究
郭辉,伍川辉,刘泽潮,黄衍,于昊明
(西南交通大学 机械工程学院,四川 成都 610031)
经验小波变换(EWT)作为自适应的信号分解方法,其分解结果与频带边界的划分密切相关。尺度空间表征(SSR)算法可以根据信号的频谱自适应地实现信号的频带划分。但是,在对轴承信号处理时SSR容易产生过度划分,这就导致一个共振频带被分解成多个分量,从而无法有效地提取故障冲击。因此,提出基于峭度准则与互相关分析的改进EWT算法:首先,根据尺度空间表征对信号的频谱进行划分;然后,计算每个分量的峭度值,对峭度值大于阈值的分量进行相关性分析,选取相关性高的分量进行合并;最后,对合并后的分量进行包络分析,提取故障冲击。通过使用仿真与实验数据对所提出的IEWT算法进行验证,证明该方法可以有效地对轴承早期微弱故障进行诊断。
尺度空间;经验小波变换;峭度;互相关分析;故障诊断

滚动轴承作为高速列车机械传动系统中应用最广泛的关键部件之一,一旦发生故障,将造成巨大的人员与经济损失。因此,针对滚动轴承的故障诊断研究具有重大现实意义。轴承的故障信号一般是非平稳、非线性信号[1-2],针对这一类信号,使用小波包变换(WPT)[3]、经验模态分解(EMD)[4]等方法可以有效地对轴承早期微弱故障冲击进行提取。WPT在进行信号分解时,其分量个数由分解层数所决定。因此,当分解层数固定时,其各个分量的频带也固定。EMD是一种自适应的信号分解算法,可以根据信号的特征自适应地实行信号的分解。但是,EMD存在模态混叠、端点效应的缺点[5],这些缺点对故障信息的提取具有严重影响很大。因此,Gilles等[6-7]结合EMD的自适应性和小波变换的理论框架等优点,提出一种新的信号处理方法即经验小波变换[8-9](empirical wavelet transform)。在此基础上,李志农等[10]将该方法应用于转子磨碰故障诊断中,区分出碰磨故障的严重程度,验证了经验小波在转子故障诊断的有效性。向玲等[11−12]通过在频域中找到2个连续极大值之间的极小值作为频域划分界限,提出IEWT和FSK联合诊断的方法,识别出齿轮和滚动轴承故障频率。但是这些方法在进行频带划分时仍然存在一个共振频带被划分为几个分量的现象[13],文献中并没有提出改善的方法。在此,本文针对共振频带过度划分的现象,在尺度空间表征的基础上根据峭度与互相关准则提出改进的IEWT 算法。首先,根据尺度空间表征对信号的频谱进行划分;然后,计算每个分量的峭度值,对分量进行筛选;再对筛选后的分量进行互相关性分析,选取相关性高的分量进行合并;最后,对合并后的分量进行包络谱分析,识别轴承的故障类型。使用IEWT算法对仿真信号与实验信号进行分析,证明IEWT算法可以有效地对轴承早期微弱故障进行诊断。
1 基本理论
1.1 EWT原理
EWT的核心是根据信号的频谱划分,自适应地构造正交小波滤波器组以提取包含故障冲击的 AM-FM 分量。
信号()的傅里叶变换为(),频率范围为Î[0,π]。ω表示频带边界的中心频率,将[0,π]划分为个频带,得到+1条边界(包含[0,π])。频谱分界示意图如图所示,每个频带可以表示为:

过度区间可以定义为以ωn为中心,宽度为Tn=2τn的区间,如图1阴影区。



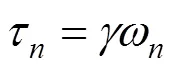

其中:傅里叶变为[∙],傅里叶反变换为−1[∙],则信号()的经验小波变换的细节系数可以由经验小波函数和信号内积产生:


()的经验小波变换的近似系数可以由尺度函数和信号内积产生:
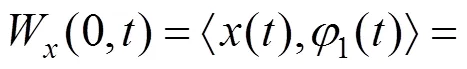
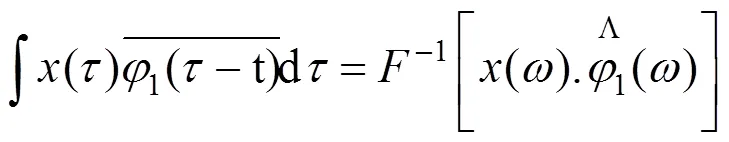
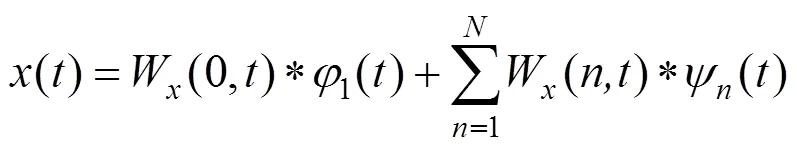
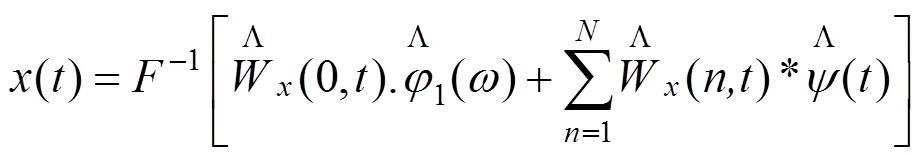

对于一个时间序列(),经过经验小波分解后可以得到

1.2 尺度空间
尺度空间方法是使用高斯函数对信号的频谱进行平滑,随着平滑次数的增加,一些虚假的频带分界点消失,而真实的分界点保留。所以每平滑1次,求取1次频带的分界点并记录下来。最后生成一张关于尺度和频带分界点的二维图像,这个图像记录的是每一次平滑后的分界点位置。尺度空间定义为:
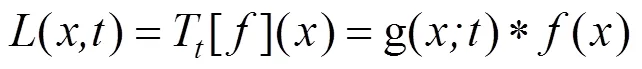
其中:*表示卷积;()表示需要平滑的信号的频谱。离散的尺度空间定义:
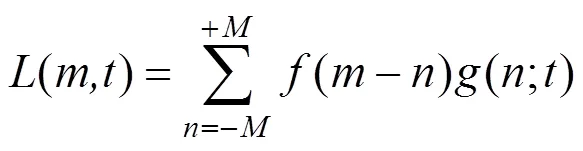
其中:为高斯核函数的长度,且

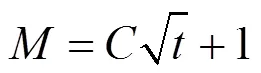
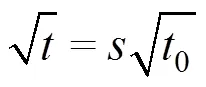
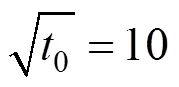
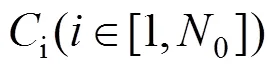

图2 尺度空间曲线
1.3 峭度
峭度是概率密度分布尖峭程度的度量,是对轴承振动信号进行时域处理最常用的无纲量参考指标,数学描述为:
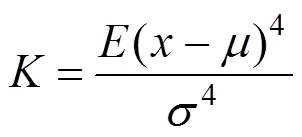
式中:为振动信号;为信号的均值;为信号的标准差。
峭度在轴承中表现出很强规律性,轴承在刚投入使用期间,其振动信号幅值分布接近正态分布,峭度值保持大约等于3。在轴承进入使用后期,出现故障的时候,信号幅值会明显偏离正态分布,峭度会随之增大,此时可以认为出现了故障初期现象,筛选出峭度值超过4的分量进行下一步计算。
1.4 互相关系数
在信号处理中,用互相关来衡量2个时间序列()和()在2个不同时刻取值之间的相似程度。对于互相关函数定义为:

互相关函数归一化处理:
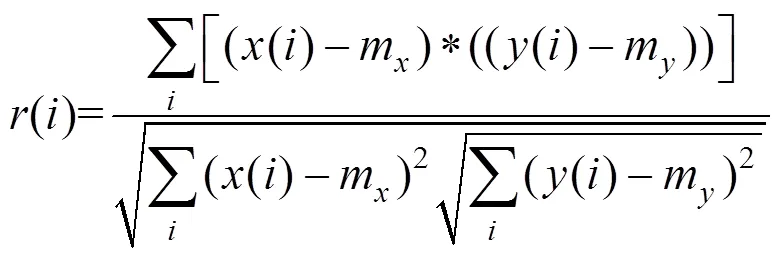
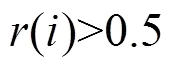
2 故障诊断流程
因为,尺度空间表征在对轴承故障信号的频谱进行划分时,容易存在过度划分,因此,本文在峭度与互相关准则的基础上提出一种改进的EWT分解——IEWT,见图3。方法诊断流程如下:
1) 对原始信号进行傅里叶变换,用尺度空间自适应地对频带进行划分。
2) 计算各个分量的峭度值,设置阈值进行筛选。
3) 筛选出的分量若存在相邻分量峭度值相近,则对相邻分量作互相关分析。
4) 若在计算相关分析结果中,相关系数超过0.5,则对相邻分量进行合并,否则不合并。
5) 对合并后的分量进行包络谱分析,找出故障频率。

图3 诊断流程图
3 仿真分析
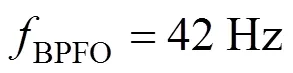
通过SSR对仿真信号进行频带划分,频带划分如图5。分解得到9个分量,计算各个分量的峭度,结果如图6所示。c5和c6的峭度值超过阈值,表明c5和c6 2个分量包含了故障频率,且分量又相邻,可能是被过度划分的共振频带,所以对其做进一步的相关性分析,结果如表1所示。由表1可知,c5和c6高度相关,说明c5和c6分量确是一个共振频带被过度划分为2个子频带,所以对其合并重构。最后对合并分量进行包络谱分析,结果如图7所示。通过对比图7~8,可以发现合并后分量信号包含更多故障频率倍频,进一步说明了算法对共振频带过度划分的现象起到了抑制作用,从而能更有效诊断出轴承早期故障。
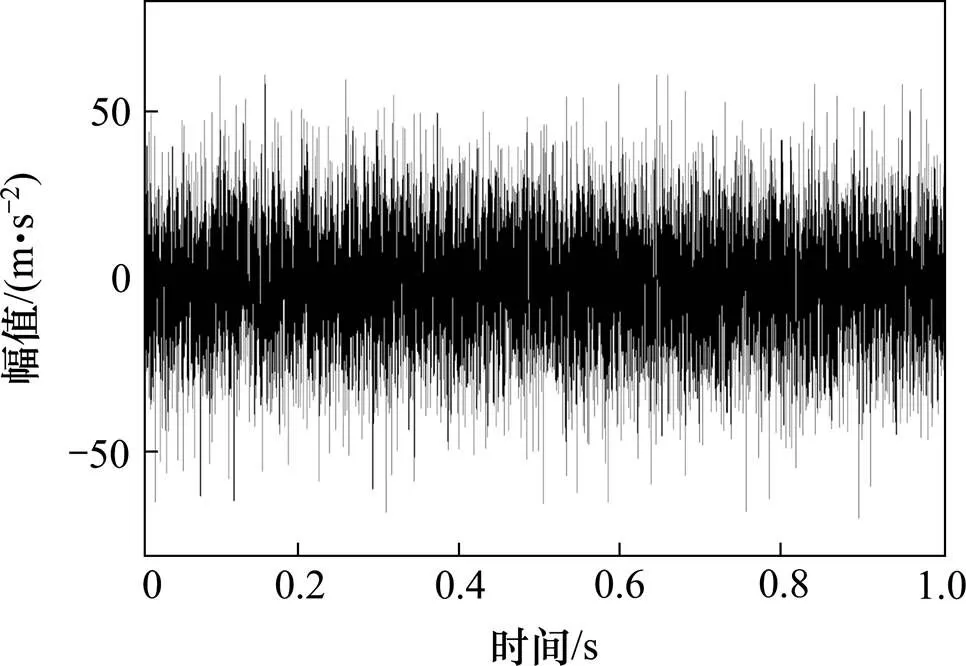
图4 仿真信号时域图
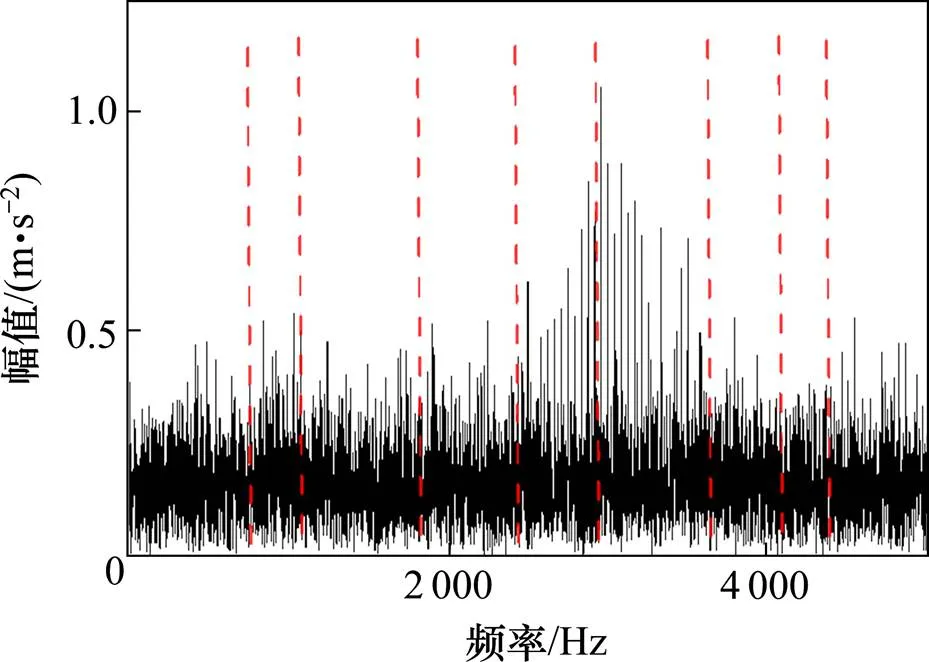
图5 SSR频带划分
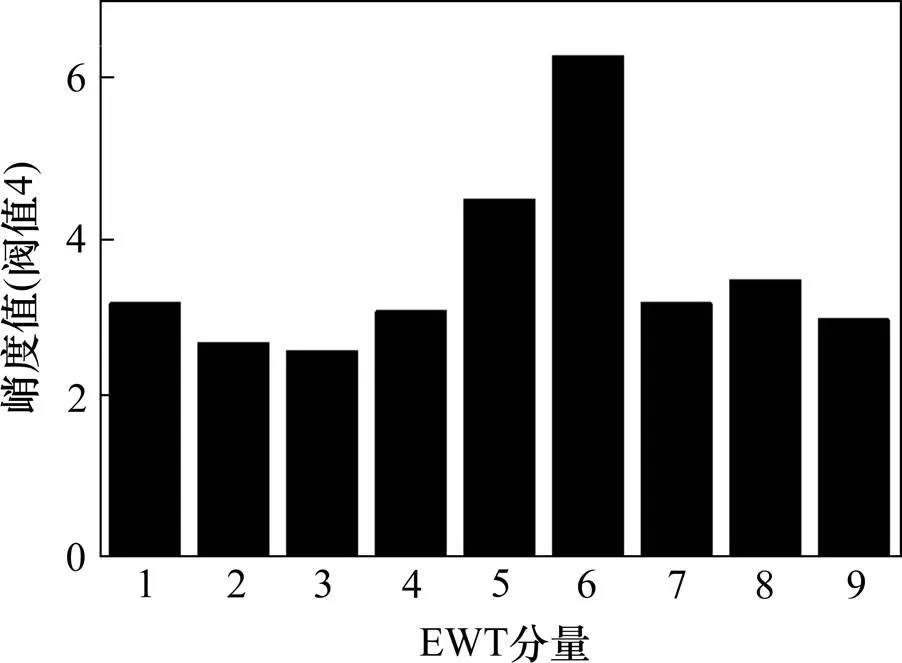
图6 IEWT分量峭度值计算结果(阈值为4)

表1 IEWT分量互相关系数计算
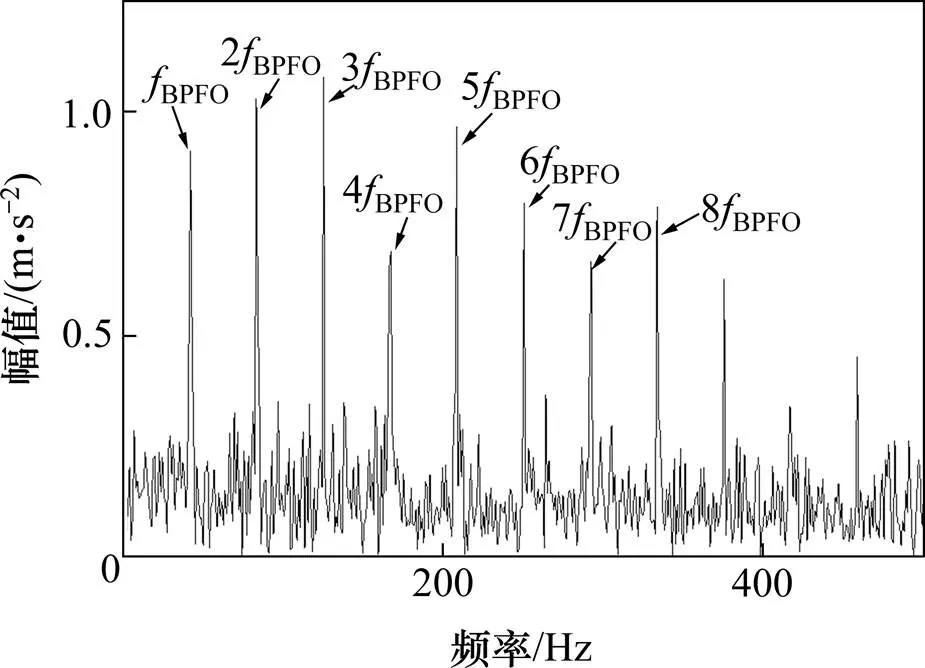
图7 合并分量频谱分析
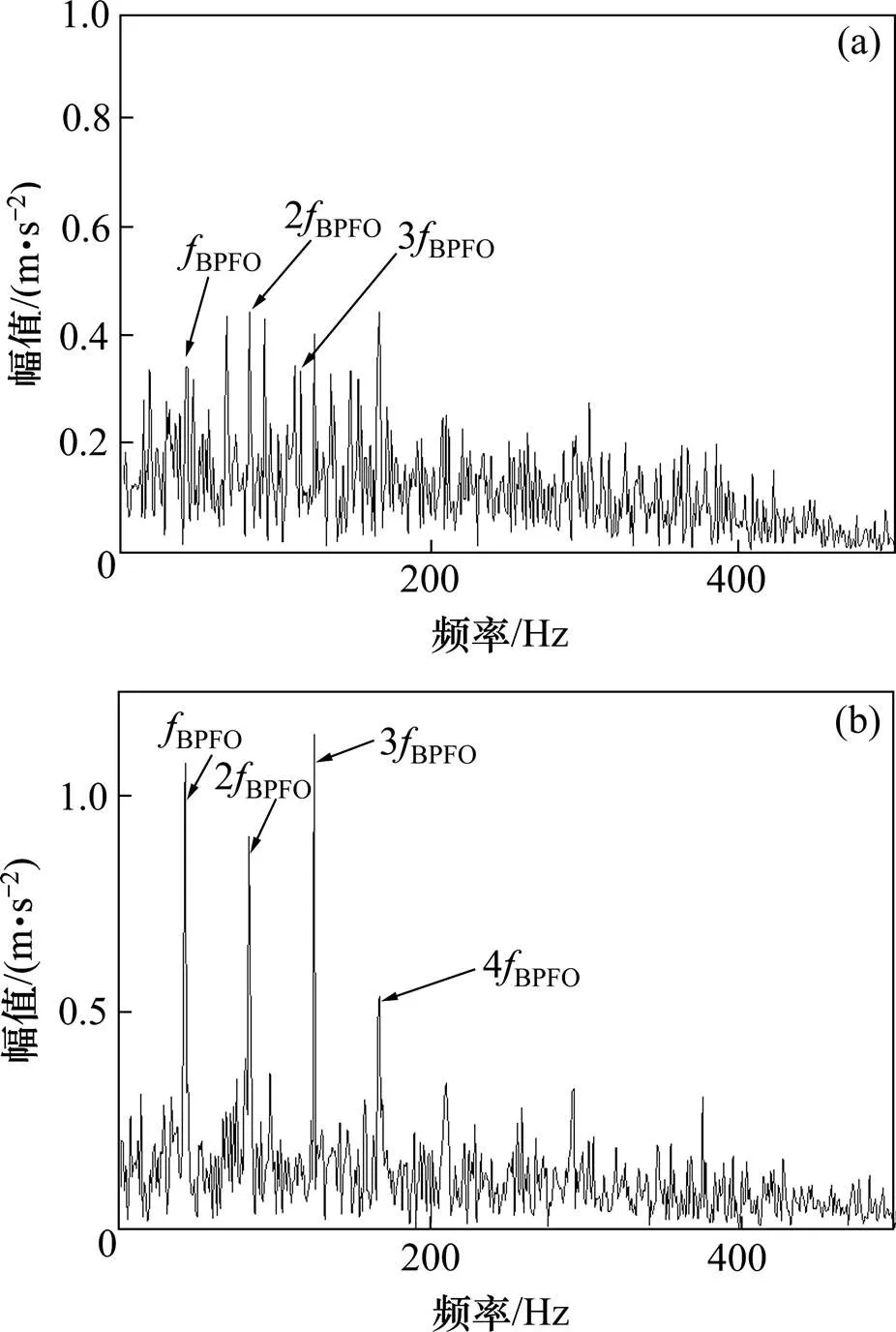
(a) c5分量频谱分析;(b) c6分量频谱分析
4 试验分析
为了进一步验证算法有效性,应用在西南交通大学牵引动力国家重点实验室试验的滚动轴承外圈故障数据进行验证,并与EWT进行对比,试验设备如图9所示。试验采样频率为10 kHz,轴旋转频率为10.28 Hz。由式(15)可知,轴承外圈故障频率BPFO= 41.65 Hz。

图9 试验台
试验信号时域波形如图10所示。根据SSR得到的频谱划分边界如图11所示,然后计算每个分量包络的峭度值,结果如图12所示。由图12可知,c2,c3和c4峭度值超过阈值,表明这三者都包含了轴承故障频率,又因为彼此相邻,可能是共振频带过度划分导致,所以对其进行互相关性分析,结果如表2所示。根据表2所示,c3和c4具有高度的相关性,说明c3和c4是一个共振频带被过度划分成的2个分量。因此,对这2个分量进行合并。合并后分量的包络谱如图13所示,图14为合并前c3和c4的包络谱。通过对比表明,图13中故障特征频率及其谐波更加明显,进一步证明了该算法对共振频带被过度划分的现象起到了抑制作用,IEWT可以更加有效地实现轴承早期微弱故障的诊断。

图10 原始数据时域图
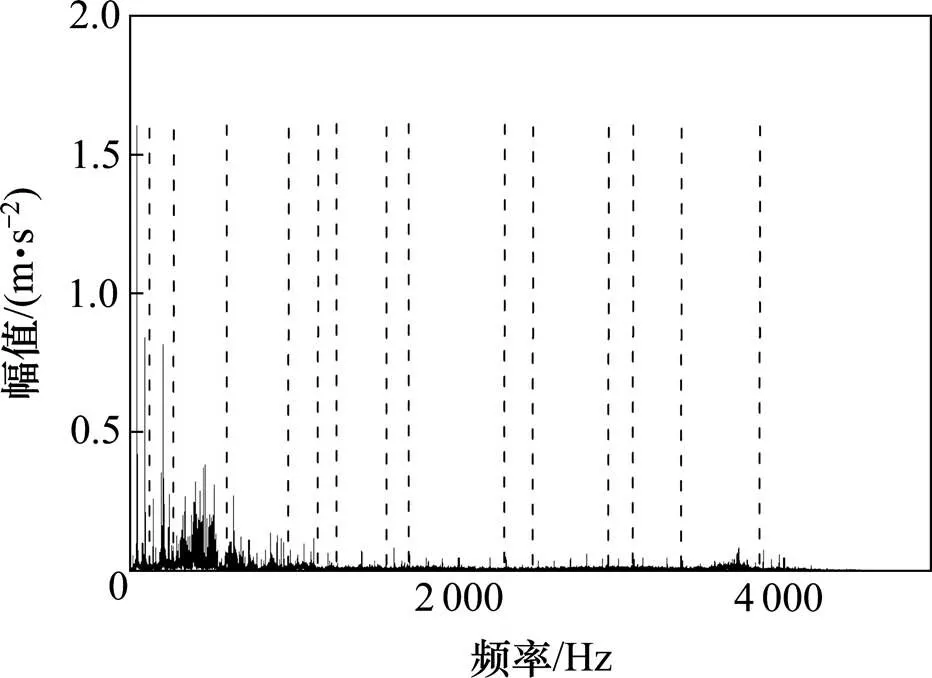
图11 SSR频带划分

图12 IEWT分量峭度值计算结果(阈值为4)

表2 IEWT分量互相关系数计算

图13 合并分量包络谱分析
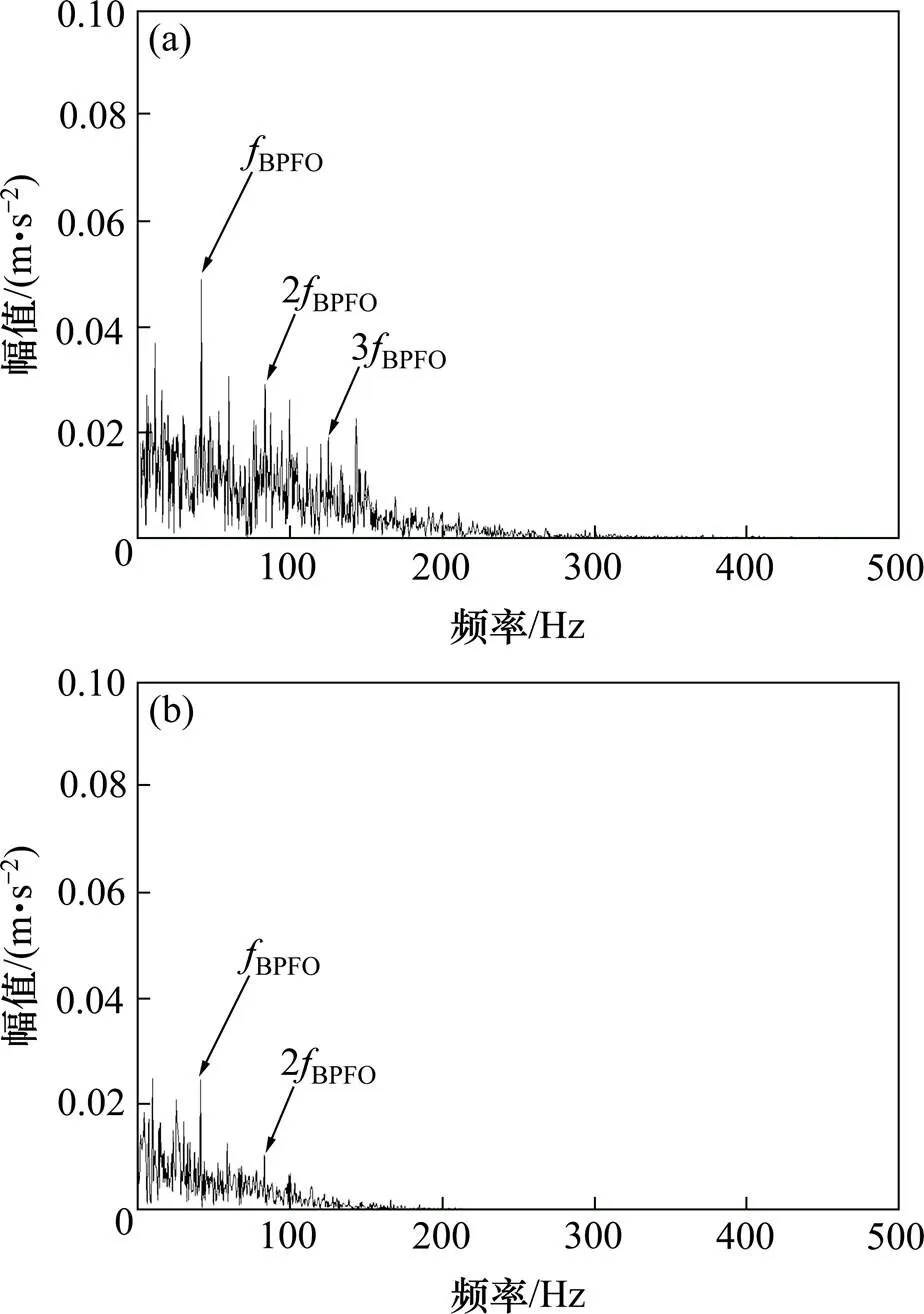
(a) c3分量频谱分析;(b) c4分量频谱分析
5 结论
1) 尺度空间表征可以自适应地实现信号频带的划分。
2) 在对轴承故障信号进行频带划分时,尺度空间表征并不能得到最优的带宽。
3) 基于峭度和互相关准则的IEWT可以得到包含故障冲击更多的频带。
[1] 向玲, 唐贵基, 胡爱军. 旋转机械非平稳振动信号的时频分析比较[J]. 振动与冲击, 2010, 29(2): 42−45. XIANG Ling, TANG Guiji, HU Aijun. Time frequency analysis of nonstationary vibration signals in rotating machinery[J]. Journal of Vibration and Shock, 2010, 29(2): 42−45.
[2] Yeh Poliang, LIU Peiling. Application of the wavelet transform and the enhanced Fourier spectrum in the impact echo test[J]. NDT and E International, 2008, 41(5): 382−394.
[3] Jivet I, Tomoroga M. Ultrasound image enhancement for visualization using spatially variant morphological filters[M]. Springer International Publishing, 2014: 255− 258.
[4] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 454: 903−995.
[5] 钟佑明, 秦树人, 汤宝平. 一种振动信号新变换法的研究[J]. 振动工程学报, 2002, 15(2): 113−118. ZHONG Youming, QIN Shuren, TANG Baoping. A new method of vibration signal transformation[J]. Journal of Vibration Engineering, 2002, 15(2): 113−118.
[6] Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999− 4010.
[7] Gilles J, Tran G, Osher S. 2D empirical transforms. Wavelets, ridgelets and curvelets revisited[J]. Siam Journal on Imaging Sciences, 2014, 7(7): 157−186.
[8] GU X, YANG S, LIU Y, et al. Rolling element bearing faults diagnosis based on kurtogram and frequency domain correlated kurtosis[J]. Measurement Science and Technology, 2016, 27(12): 125−129.
[9] GU X, YANG S, LIU Y, et al. Compound faults detection of the rolling element bearing based on the optimal complex Morlet wavelet filter[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232(10): 1786− 1801.
[10] 李志农, 朱明, 褚福磊, 等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报, 2014, 35(11): 2423−2432. LI Zhinong, ZHU Ming, CHU Fulei, et al. Research on Mechanical Fault Diagnosis Based on Empirical Wavelet Transform[J]. Journal of Instrumentation, 2014, 35(11): 2423−2432.
[11] 向玲, 高雪媛, 张力佳, 等. IEWT和FSK在齿轮和滚动轴承故障诊断中的应用[J]. 振动、测试与诊断, 2017, 37(6): 1256−1261. XIANG Ling, GAO Xueyuan, ZHANG Lijia, et al. Application of IEWT and FSK in fault diagnosis of gears and rolling bearings[J]. Vibration, Testing and Diagnosis, 2017, 37(6): 1256−1261.
[12] 李媛媛. 基于经验小波变换的机械故障诊断方法[D]. 北京: 华北电力大学, 2016: 1−50. LI Yuanyuan. Mechanical fault diagnosis method based on empirical wavelet transform[D]. Beijing: North China Electric Power University, 2016: 1−50.
[13] Antoni J, Randall R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Systems and Signal Processing, 2006, 20(2): 308−331.
[14] LIANG Ming, Soltani Bozchalooi I. An energy operator approach to joint application of amplitude and frequency- demodulations for bearing fault detection[J]. Mechanical Systems and Signal Processing, 2010, 24(1): 1473−1494.
Research on fault diagnosis method of IEWT bearing based on kurtosis and cross correlation
GUO Hui, WU Chuanhui, LIU Zechao, HUANG Yan, YU Haoming
(School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Empirical wavelet transform (EWT) was an adaptive signal decomposition method, and its decomposition result was closely related to the division of frequency band boundaries. The Scale Space Representation (SSR) algorithm can adaptively implement the frequency band division of the signal according to the spectrum of the signal. However, the SSR is prone to transitional division when processing the bearing signals, which causes one resonance frequency band to be decomposed into a plurality of components, so that the fault impact cannot be effectively extracted. Therefore, this paper proposes an Improved EWT algorithm based on kurtosis criteria and cross-correlation analysis. First, the spectrum of the signal was divided according to the scale space representation. Then, the kurtosis value of each component was calculated, and the component with the kurtosis value greater than the threshold was calculated. Correlation analysis was performed, the components with high correlation for merging was selected; Finally, perform envelope analysis on the combined components to extract the fault impact. The proposed IEWT algorithm was verified by using simulation and experimental data, which proves that the method can effectively diagnose the early weak faults of the bearing.
scale space; empirical wavelet transform; kurtosis; cross correlation analysis; fault diagnosis
TH133.33;TN911.72
A
1672 − 7029(2019)07− 1774 − 07
10.19713/j.cnki.43−1423/u.2019.07.023
2018−09−25
国家重点研发计划先进轨道交通重点专项资助项目(2017YFB1201004)
伍川辉(1964−),男,四川成都人,副教授,从事先进测控技术及应用研究;E−mail:chwu126@126.com
(编辑 阳丽霞)
