塑性铰区纵筋加密的少筋混凝土桥墩振动台试验研究

李佳文，丁明波，鲁景华，王海雷，李传喜，刘正楠

塑性铰区纵筋加密的少筋混凝土桥墩振动台试验研究

李佳文，丁明波，鲁景华，王海雷，李传喜，刘正楠

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

为探究少筋混凝土重力式桥墩塑性铰区纵筋加密设计思路的合理性，以配筋为0.3%的少筋混凝土重力式矩形桥墩为原型设计制作缩尺比例模型，并在此基础上，设计提出墩底塑性铰区局部纵筋加密的对比模型，采用El-Centro波模拟地震进行振动台试验，测试2种模型的破坏模式及桥墩墩顶位移与加速度时程反应。对比研究塑性铰区纵向钢筋加密后桥墩的抗震性能，试验研究结果表明塑性铰区纵筋加密设计的桥墩具有良好的抗震性能，说明了此方案的合理性。

少筋混凝土；重力式桥墩；局部配筋加密；振动台试验；破坏模式

我国是一个多地震的国家，桥梁工程是铁路工程中受地震破坏最严重的结构物。我国高速铁路广泛采用少筋混凝土重力式桥墩，由于其截面尺寸大、刚度大以及自重大等特点，致使其在地震中受到的地震力亦大[1]。针对此结构破坏部位一般发生在墩底，修复需墩底与基础锚固[2]，本试验对比模型针对此薄弱部位进行加强，设计塑性铰区纵筋局部加密模型，并探究其在地震作用下的破坏模式。目前，利用振动台试验研究少筋混凝土重力式桥墩的课题较少，蒋丽忠等[3]通过拟静力试验研究圆端形高速铁路重力式桥墩，认为纵筋配筋率较低时桥墩滞回曲线呈现出捏缩状。陈兴冲等[4]采用拟静力试验讨论少筋混凝土重力式桥墩的抗震性能与纵筋配筋率的关系。鞠彦忠等[5]对低配筋模型桥墩进行拟静力试验，得到其延性与配筋的关系。司炳君等[6]利用ANSYS软件模拟得到圆形钢筋混凝土桥墩的滞回曲线及骨架曲线，并与试验结果进行对比，验证了模型的正确性。振动台试验是研究结构地震反应最直接的方法，可以实时再现真实地震作用或人工地震作用全过程[7]。申彦利等[8]通过振动台试验研究钢筋混凝土空心矩形桥墩的抗震性能。Patrick等[9]制作2个缩尺比例为1/3的钢筋混凝土原型桥墩，进行了振动台试验研究，结果显示，与拟静力试验相比，振动台试验下桥墩抗震性能提升，延性更高。Junichi等[10]对钢筋混凝土桥墩进行三向多维地震输入的振动台试验，结果表明多向地震激励比单向激励下的动力响应要大，且水平动力响应不受竖向激励的影响。Arash等[11]对双柱式桥墩进行振动台试验研究，采用FRP管−混凝土组合材料对比传统钢筋混凝土材料，结果表明，组合材料的墩柱耗能大，塑性铰区高度为传统模型的2倍。目前，针对少筋混凝土桥墩进行振动台试验的研究较少。这种结构变形性能较差，在地震中容易受到破坏[12]，有必要利用振动台试验的方法探究其抗震性能与破坏模式。本文以配筋率为0.3%的少筋混凝土重力式桥墩进行研究，设计一个配筋率为0.3%的模型桥墩，以此为基础设计另一个配筋0.3%且塑性铰区局部额外加密0.2%的对比模型，利用振动台试验，采用El-Centro波对其进行分级加载，得到不同峰值加速度(PGA)作用下的墩顶位移和加速度时程曲线，并得到其破坏模式。

1 模型桥墩及振动台试验

1.1 模型桥墩的相似系数

本试验研究的混凝土实体桥墩为8度地震区圆端形桥墩，桥墩图号采用兰乌二线施(普)桥参01，墩高9.0 m，跨度12 m，横截面为(0.95+1.7+0.95)× 1.9 m2，主梁采用跨度为12 m的T梁。综合考虑实际加载条件，根据惯性矩不变原则将圆端形桥墩转换为矩形桥墩，转换后的矩形截面为1.8 m×3.1 m。

综合考虑试验室现有条件，选定几何相似系数为1/15，表1为模型相似系数。

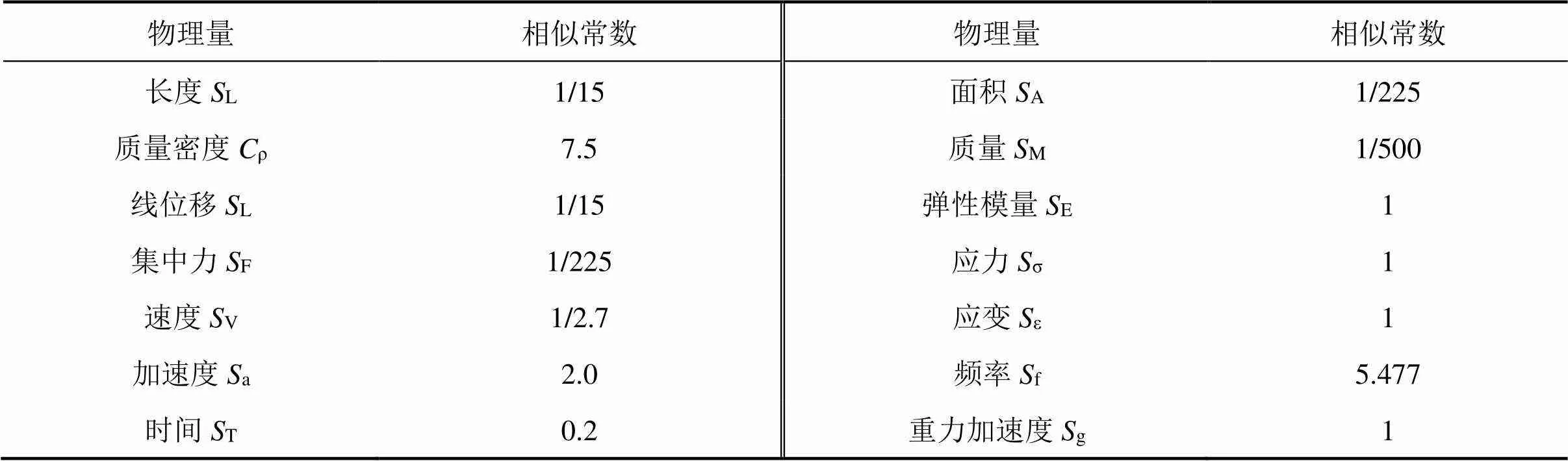
表1 模型主要相似系数

1.2 模型的尺寸、材料以及配重

本桥原型为铁路中常用的简支梁桥，简化成单墩模型来进行试验，按相似系数严格设计桥墩的几何尺寸和配筋[13]，图1为桥墩模型的试验加载图。其中墩顶配重用钢板制作的装有铁砂的铁箱实现，桥墩底座与振动台用螺栓固结。

单位：mm

桥墩模型纵筋采用f4光圆钢筋，箍筋采用f3的10号铁丝，间距为100 mm，设计保护层为9 mm。模型桥墩采用与原型相同的C30混凝土，共制作2个模型，模型Ⅰ为配筋率0.3%的桥墩，模型Ⅱ为全桥配筋0.3%底部纵筋加密0.2%的桥墩，纵筋加密的长度范围是依据等效塑性铰区的长度设定，参考中国《公路桥梁抗震设计细则》(JTG/T B02−01− 2998)：p=2/3=80 mm，结合日本JRA规范规定的：p=0.2−0.1=108 mm，考虑到纵筋加密后桥墩破坏区域向上发展，本试验偏保守取值150 mm。加密钢筋与普通配筋采用同样尺寸与型号的钢筋，在桥墩长边两侧均匀布置在两纵筋中间，使其能更好地发挥抵抗纵向输入地震荷载的作用，并在端点处设计弯起，防止滑移，此外另布置一道箍筋与加密纵筋连接，弯起搭接在箍筋上。浇筑中留置标准试块3组(150 mm×150 mm×150 mm)，标准养护下，强度满足要求。模型图如图2所示。采用Midascivil建立有限元模型验证缩尺模型的正确性，利用直接施加节点荷载来模拟上部配重，得出桥墩原型与模型的1阶模态，见图3，对比计算得知原桥墩周期为0.218 s，缩尺后的为0.039 3 s，按照动力相似比周期的相似常数为1/5.477，得出墩顶配重480 kg合理。

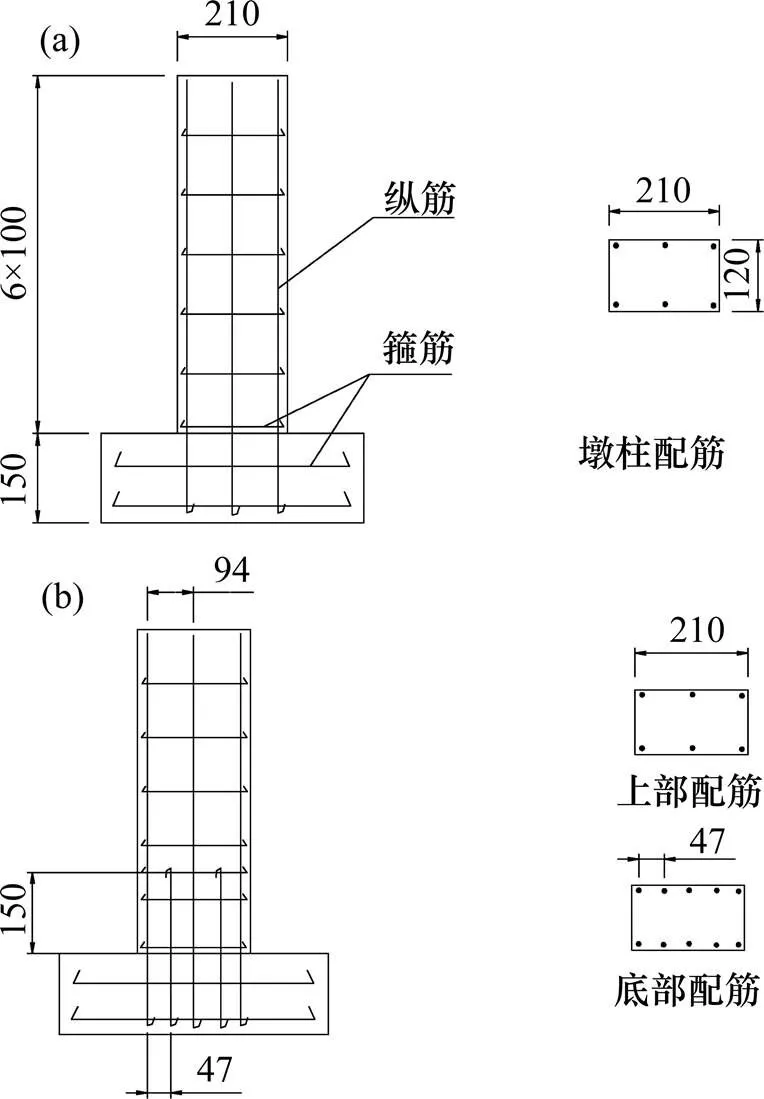
单位：mm

(a) 墩台原型1阶振型(T=0.218 s)；(b) 墩台模型1阶振型(T=0.039 3 s)

1.3 测点布置及试验仪器

本试验用2个日本松下 Panasonic-HL-G108- S-J激光位移计测动态时程位移，一个布置在墩顶，由于墩底与台面固结，另一个激光位移计布置在台面；用加速度计(电压灵敏度为50.39 mV/ms−2，频率范围为0.5~3 000 Hz)墩顶和台面各布置一个，分别测墩顶和墩底的纵桥向水平加速度，并且加以台面自带加速度计辅助使用，记录台面实际地震动的加速度时程，墩底两侧各贴两个电阻应变片，测点布置如图4所示。

图4 测点布置图

自20世纪80年代以来，国内外在研制地震模拟振动台试验技术方面有了较大发展[14]，2005年，日本建成了目前世界最大的振动台E-Defense[15]，全称为“三维原型地震试验设备”。本试验所采用的振动台为ES-10-240振动台，该振动台额定正弦最大推力为10 kN，额定随机最大推力10 kN，额定冲击最大推力20 kN，频率范围1~3 000 Hz，最大加速度500 m/s2，最大速度1.8 m/s，最大位移±25 mm，工作台面为镁铝合金材料其尺寸为500 mm×700 mm，台面竖向最大负载500 kg。本试验在兰州交通大学甘肃省道路桥梁与地下工程重点试验室进行。

1.4 试验地震波的处理

本试验选用El-Centro地震波(1940 N-S向)，对桥墩模型进行纵向加载，该原始波的峰值加速度为0.355 69，持续时长为53.72 s。试验室实际加载在模型上的地震波按照动力相似T=0.2，将原始波记录持续时间进行了全过程压缩，研究2个模型在逐级递增的峰值加速度地震荷载作用下的地震反应。图5为全过程压缩后PGA为0.3的El-Centro波。

图5 试验用PGA为0.3g的El-Centro地震波

1.5 试验加载工况

本试验2个模型都为纵向输入地震波，考虑在承载范围之内的所有放大倍数的地震波，输入PGA依次为0.1，0.2，0.3，0.4，0.5，0.6和0.8，观察每一工况的试验现象，受力状况，确定2种不同模型的易损位置。表2列出试验所有工况。

表2 振动台试验工况一览表

2 试验现象与结果分析

2.1 试验现象

2组模型在工况1，2和3墩底均没有出现裂缝。随着PGA的增大，输入地震荷载峰值加速度达到0.4时，模型Ⅰ和模型Ⅱ保护层均出现裂缝，裂缝还未贯穿整个墩身，模型Ⅰ在墩底2 cm处出现裂缝，模型Ⅱ在距离墩底10 cm处出现裂缝(加密高度距离墩底为15 cm)，由于塑性铰区纵筋加密使得破坏部位上移；输入地震峰值荷载加速度达到0.6时，裂缝扩展，贯穿整个墩身，核心混凝土开裂，裂缝在输入的地震荷载作用下一张一合清晰可见，顶部位移持续增大。模型Ⅱ墩底与承台连接完好，若需要震后快速修复，只需墩身裂缝周围外包图纤维布、外包混凝土或外包钢板[2]即可，无需考虑墩底与基础的锚固，节约成本和时间。图6~7为裂缝发生部位示意图。

单位：mm

2.2 地震响应分析

墩顶位移与墩顶加速度时程反应是结构在地震过程中动态响应的指标，也最能体现出抗震性能的变化。

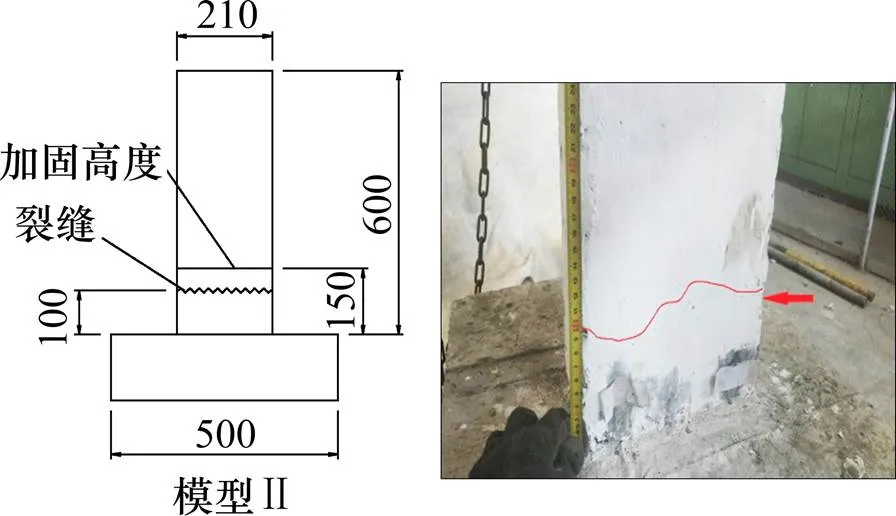
单位：mm

2.2.1 墩顶位移极值与时程曲线

通过记录地震荷载作用下墩顶和墩底绝对位移，计算得到墩顶相对墩底的位移，取其极值进行研究，以此评价模型在位移响应方面的抗震性能。表3为各个工况下墩顶相对墩底的位移极值。从表3可以看出，裂缝未发生前，模型Ⅱ比模型Ⅰ位移少45%以上；保护层开裂但裂缝未贯通前，模型Ⅱ比模型Ⅰ位移少20%~45%；直至裂缝贯通模型Ⅱ比模型Ⅰ位移少9%。由于其底部纵筋加密，致使墩顶位移极值自始至终一直小于一般配筋模型。以上表明底部塑性铰区纵筋加密能减小墩顶位移，更能保证在地震作用下其上部结构的稳定，能避免由于上端位移过大使其落梁的震害。图8~9为部分试验位移时程曲线。

试验表明，每个工况下，模型Ⅱ的墩顶位移极值总是小于模型Ⅰ的，整个构件在地震作用下更有利于上部结构的稳定。

图8 峰值加速度为0.4g时的位移时程曲线

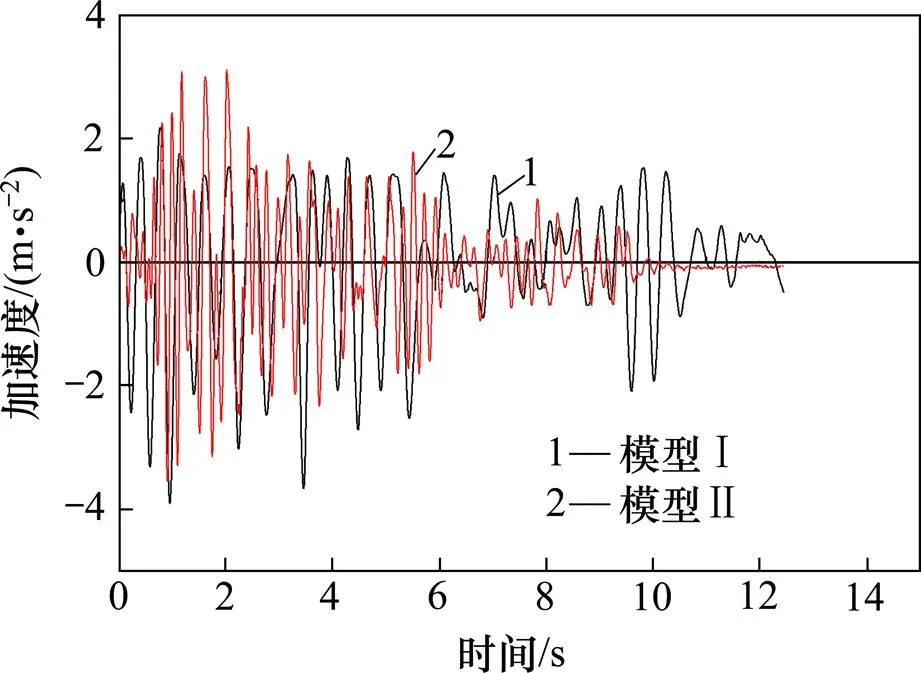
图9 峰值加速度为0.8g时的位移时程曲线

表3 各工况下的墩顶位移极值

2.2.2 墩顶加速度极值与时程曲线

本试验通过2个加速度计分别记录地震荷载作用下墩顶和墩底加速度时程反应，用以研究模型在不动地震设防烈度作用下的加速度变化规律，以此评价模型在加速度响应方面的抗震性能，取其极值进行研究。表4为各个峰值加速度下墩顶加速度 极值。

从表4得知，试件开裂前，模型Ⅱ的墩顶加速度都小于模型Ⅰ的；自输入峰值加速度为0.4时，即发生开裂后，模型Ⅱ的墩顶加速度普遍大于模型Ⅰ的，传递到墩顶的加速度值增大，直至达到0.8时，裂缝贯通，裂缝上下混凝土的碰撞使得加速度值呈现无规律性。图10~图11为部分试验加速度时程曲线。

表4 各工况下的墩顶加速度极值

图10 峰值加速度为0.4g时的加速度时程曲线

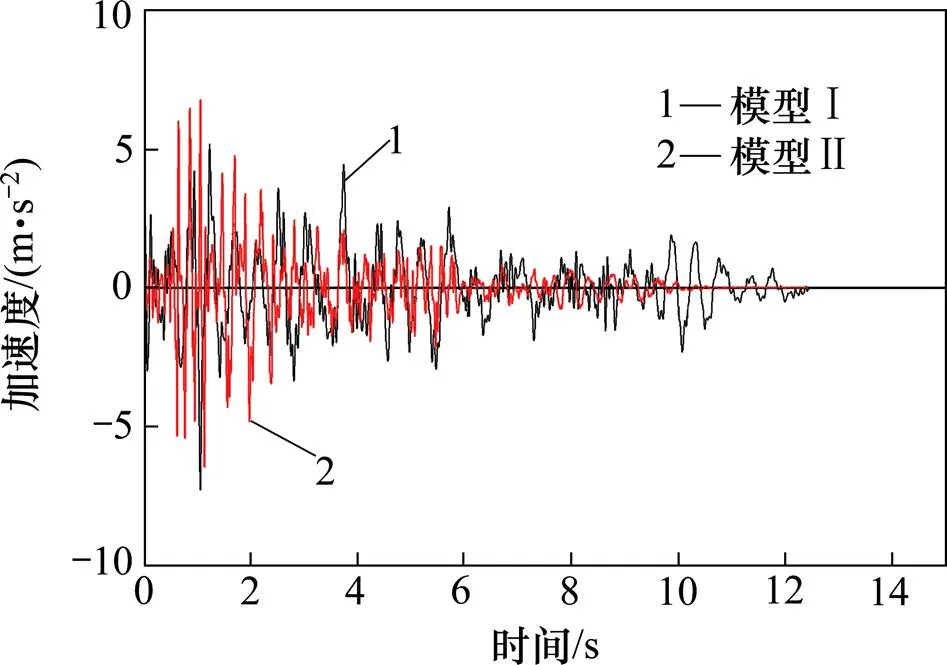
图11 峰值加速度为0.8g时的加速度时程曲线

在小震状态下，模型Ⅱ加速度一直小于模型Ⅰ的；大震作用下，模型Ⅱ裂缝上部的墩高小于模型Ⅱ的，连接裂缝上下的钢筋更多，发挥更大的作用，传递到上部的加速度值比模型Ⅰ大。

3 结论

1) 通过振动台试验发现，经过纵筋加密的模型裂缝发生位置上移，墩底与基础连接完好，震后若要实现快速修复，无需考虑墩底与基础的锚固，可节约修复时间与成本。

2) 经过塑性铰区纵筋局部加密的模型位移极值小于一般配筋模型，试验表明，保护层开裂前少45%以上；裂缝贯通全截面前少20%以上；全截面开裂后少9%，更能保证上部结构在地震作用下的稳定。

3) 裂缝发生前，模型Ⅱ墩顶加速度小于模型Ⅰ的；裂缝发生后，模型Ⅱ的墩顶加速度大于模型 Ⅰ的。

4) 通过振动台试验，验证了少筋混凝土重力式桥墩塑性铰区局部加密设计思路的合理性，抗震效果提升的同时，钢筋用量少，更为经济。

[1] 陈兴冲, 张永亮, 丁明波, 等. 罕遇地震下少筋混凝土桥墩最低配筋率研究[J]. 桥梁建设, 2016, 46(5): 24−28. CHEN Xingchong, ZHANG Yongliang, DING Mingbo, et al. Study of minimum reinforcement ratios for concrete piers arranged with small amount of reinforcement under rare earthquake[J]. Bridge Construction, 2016, 46(5): 24− 28.

[2] 丁明波. 铁路重力式桥墩抗震加固方法研究[D]. 兰州:兰州交通大学, 2013. DING Mingbo. Research on seismic retrofit methods for railway bridge with gravity piers[D]. Lanzhou: Lanzhou Jiaotong University, 2013.

[3] 蒋丽忠, 邵光强, 姜静静, 等. 高速铁路圆端形实体桥墩抗震性能试验研究[J]. 土木工程学报, 2013, 46(3): 86−95. JIANG Lizhong, SHAO Guangqiang, JIANG Jingjing, et al.Experimental study on seismic performance of solid piers with round ended cross-section in high-speed railway[J].China Civil Engineering Journal, 2013, 46(3): 86−95.

[4] 陈兴冲, 张永亮, 丁明波, 等. 少筋混凝土重力式桥墩抗震设计方法研究[J]. 铁道工程学报, 2016, 33(3): 76− 80.CHEN Xingchong, ZHANG Yongliang, DING Mingbo, et al. Research on the seismic design method for concrete gravity piers with low longitudinal reinforcement ratio[J].Journal of Railway Engineering Society, 2016, 33(3): 76−80.

[5] 鞠彦忠, 阎贵平, 刘林. 低配筋大比例尺圆端型桥墩抗震性能的试验研究[J]. 土木工程学报, 2003, 36(11): 65−69. JU Yanzhong, YAN Guiping, LIU Lin. Experimental study on seismic behavors of large-scale RC round-ended piers with low reinforcement ratio[J]. China Civil Engineering Journal, 2003, 36(11): 65−69.

[6] 司炳君, 孙治国, 艾庆华, 等. 钢筋混凝土桥墩滞回性能的有限元参数敏感性分析及模型改进[J]. 工程力学, 2009, 26(1): 174−180.SI Bingjun, SUN Zhiguo, AI Qinghua, et al. Sensitive analysis and model modification for finite element analysis of R/C bridge piers under cyclic loading[J]. Engineering Mechanics, 2009, 26(1): 174−180.

[7] 蔡新江, 田石柱. 振动台试验方法的研究进展[J]. 结构工程师, 2011, 27(增1): 42−46.CAI Xingjiang, TIAN Shizhu. research advance of shaking table testing method[J]. Structual Engineers. 2011, 27(Suppl 1): 42−46.

[8] 申彦利, 谷少康. 钢筋混凝土空心矩形桥墩振动台试验[J]. 建筑科学与工程学报, 2018, 35(5): 128−133. SHEN Yanli, GU Shaokang. Shake table test for reinforced concete hollow rectangular pier[J]. Journal of Architecture and Civil Engineering. 2018, 35(5): 128−133.

[9] Patrick Laplace, David Sanders, Saiid Saiidi M, et al. Shake table testing of flexure dominated reinforced concrete bridge columns[R]. Report No. CCEER 99-13.A report for the California Department of Transportation Sacramento, California, 1999.

[10] Junichi Sakai, Shigeki Unjoh. Earthquake simulation test of circular reinforced concrete bridge column under multidirectional seismic excitation[J]. Earthquake Engineering and Engineering Vibration, 2006, 5(1): 103− 110.

[11] Arash E Zaghi, Saiid Saiidi M, Amir Mirmiran. Shake table response and analysis of a concrete-filled FRP tube bridge column[J]. Composite Structures, 2012, 94: 1564− 1574.

[12] 李娜. 铁路钢筋混凝土重力式桥墩抗震性能研究[D].西安: 长安大学, 2011. LI Na. Study of seismic performance of railway reinforced concrete gravity bridge pier[D]. Xi’an: Chang’an University, 2011.

[13] 马坤全. 铁路重力式桥墩桥梁抗震性能及抗震措施研究[J]. 铁道学报, 2000(增1): 71−75. MA Kunquan.Research on seismic character and earthquake resistance measures for railway bridge with gravity piers[J].Journal of the China Railway Society, 2000(Suppl 1): 71−75.

[14] 李勇, 闫维明, 刘晶波, 等. 桥梁结构缩尺模型模拟地震振动台试验研究进展[J]. 工程抗震与加固改造, 2013, 35(5): 1−10.LI Yong, YAN Weiming, LIU Jingbo, et al.Study and development on shake table tests of scaled models of bridge engineering[J].Earthquake Resistant Engineering and Retrofitting. 2013, 35(5): 1−10.

[15] Nakamura I, Shimizu H, Minowa C, et al. E-Defense experiments on full-scale wooden house[C]// The 14th World Conference on Earthquake Engineering (WCEE). Beijing, 2008.

Shaking table test of reinforced concrete pier with longitudinal reinforcement encrypt in plastic hinge area

LI Jiawen, DING Mingbo, LU Jinhua, WANG Hailei, LI Chuanxi, LIU Zhengnan

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 200240, China)

In order to explore the rationality of the design concept of reinforced concrete pier with longitudinal reinforcement in plastic hinge area of gravity concrete piers with low reinforced concrete, in this paper, a concrete gravity rectangular pier reinforced with 0.3% was designed according to the scale ratio of the prototype pier, and a comparative model of local longitudinal reinforcement in the plastic hinge area of the pier bottom was designed based on the scaled model. The shaking table test was carried out by the wave simulation earthquake using El-Centro, the failure mode of the local longitudinal reinforcement bridge pier in the general reinforcement and plastic hinge area is compared, and the displacement and acceleration time-history reaction of two contrast models are tested. The seismic behavior of the pier after the longitudinal reinforcement is encrypt in plastic hinge area is compared. The results show that the piers with longitudinal reinforcement in the plastic hinge area have good seismic performance, and the rationality of this scheme is explained.

concrete with low longitudinal reinforcement ratio; gravity type pier; local reinforcement encryption; experiment on shaking table; damage characteristic

U442.55；U448.217

A

1672 − 7029(2019)07−1728 − 07

10.19713/j.cnki.43−1423/u.2019.07.017

2018−10−15

国家自然科学基金资助项目(51768036)

丁明波(1975−)，男，山东日照人，副教授，博士，从事桥梁工程、防灾减灾工程、桥梁抗震及加固研究；E−mail：447897524@qq.com

(编辑 阳丽霞)