Kuramoto-Tsuzuki方程的Grank-Nicolson 差分格式

周丽，岳超慧

安徽农业大学应用数学系， 安徽 合肥 230031

0 引言

Kuramoto-Tsuzuki 方程描述了在歧点附近两个分支系统的行为状况[1].一维Kuramoto-Tsuzuki 方程混合初边值问题为

其中,Ω=(0,1),c1,c2为实数,u(x,t),u0(x)为复函数.

以上都是考虑一维Kuramoto-Tsuzuki 方程混合初边值问题，二维情况下对Kuramoto-Tsuzuki方程数值解的研究很少出现, 困难在于二维下非线性项|u|2u很难处理. 类似于Kuramoto-Tsuzuki方程的二维问题在文献[7]中研究了λ-ω型反映扩散系统, 作者构造了全离散的有限元逼近格式并证明了数值解的收敛性.

1 格式的建立

本文考虑下面二维Kuramato-Tsuzuki 方程混合初边值问题:

ut=(1+ic1)Δu+u-(1+ic2)|u|2u(x,t)∈Ω×(0,T]

(1)

(2)

(3)

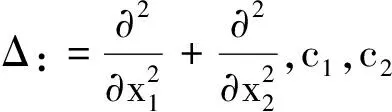
设v={vij|0≤i,j≤M},ω={ωij|0≤i,j≤M}为Ωh上的网格函数, 定义内积和范数

对方程(1)～方程(3)建立如下线性化Crank-Nicolson 型差分格式

(4)

(5)

2 解的存在性

首先引入下面的Brouwer不动点定理[8,9].

将(4)改写为

当v∈CM+1时, 分别将(Δhv,v)h,|v|1,h按定义展开得到

因此

对上式两边同时取实部得

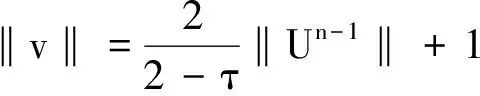
3 截断误差

(1)当1≤i,j≤M-1,0≤n≤N时

而

因此

(2)当i,j=0,M时，由于

因此可得，当i=0,M时有

(1)式两边对x1求导

可得当i=0,M时

由于

所以

因此

而

因此由以上分析可得

同理可得

定理证毕.

4 先验估计

‖Un‖h≤C‖U0‖h0≤n≤N

其中，C=C(T).

两边取实部得

由离散Gronwall不等式得

‖Un‖h≤C‖U0‖h0≤n≤N

‖U‖q,h≤C‖U‖k,p,h

|Un|1,h≤C0n=0,1,2,…,N

其中，C0=C0(u0,T).

证明 用数学归纳法证明：当n=0时,引理显然成立, 假设第n-1层结论成立|Un-1|1,h≤C0′,其中C0′是依赖于u0，T的常量.

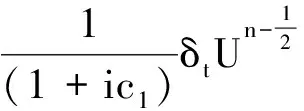
两边同时取实部得

因此

由引理2,引理3和归纳假设

‖Un-1‖8,h≤C‖Un-1‖1,2,h

是有界的.由引理3得

因此

当τ充分小时, 由离散Gronwall 不等式可得

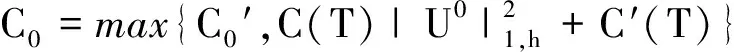
|Un|1,h≤C0(u0,T)

5 解的唯一性

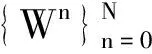
用数学归纳法证明解的唯一性.假设En-1=0,即Un-1=Wn-1，可以得到

两边同时取实部

当τ充分小时

因此有归纳假设可得‖En‖h=0,即解唯一.

6 解的收敛性

‖Un-u(tn)‖h≤C(τ+h2) |Un-u(tn)|1,h≤C(τ+h2)

证明 由于

其中

(6)

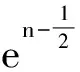
(7)

假设u(x,t)在Ω×(0,T]有界, 则

由引理3知

由引理3

两边同时取实部得

当τ充分小时, 由离散Gronwall 不等式得到

‖en‖h≤C(τ+h2)

(8)

由于

即

由引理3

当τ充分小时, 由式(8) 递推可得

|en|1,h≤C(τ+h2)

命题得证.