为大汗献出天文与算术之钥
2019-03-22陈巍


陈巍,理学博士,现为中国科学院自然科学史研究所副研究员。主要研究科技知识在古代世界的传播并把世界连为一体的历程。喜爱“上穷碧落下黄泉”,品鉴各个文明在应对相似问题时展现出的智慧。
在长达近千年之间,中世纪伊斯兰世界高举的对知识和学术的火炬,几乎只是在各个王朝都城之间传递,而并没有熄灭。尽管思想创新的自由流动逐渐受到限制,但至少在15世纪初,从北非到安纳托利亚,再到中亚,新的学术中心在继续形成。其中,在中亚阿姆河与锡尔河之间(即“河中地区”),帖木儿汗国兴盛一时。它继承了此前各个大型伊斯兰政权把首都建设为文化与学术中心的壮志,经过帖木儿大帝、沙哈鲁和兀鲁伯3代大汗的建设,帝国都城撒马尔罕聚集了大批各个领域的英才。这批学者中最著名的,当属天文学家和数学家阿尔,卡西(Jamshid al-Kashi.1380-1429)和诗人鲁米。前者以其制作天文仪器的杰出才能,以及《算术之钥》中的众多成就,不仅成为服务兀鲁伯学术爱好的得力助手,同时也在科技史上留下显赫声名。
学者生涯
1380年,阿尔·卡西生于现伊朗中部的文化城市卡尚,当时此地受帖木儿汗国控制。他早年生活似乎比较动荡,因而有努力向学改变命运的想法。但我们并不清楚他早年的成长与求学经历,只能从1406年在卡尚的一次月食观测中看到卡西最早的学术印迹。次年,他将一本天文学著作《天国阶梯》献给当地长官。此后他不断向更高层级的贵族呈现学术著作以寻求庇护和资助。最终,他的成就得到当时还是太子的兀鲁伯的注意,后者不但是王储,还热衷于天文观测,正在撒马尔罕准备兴建规模庞大的天文台,卡西关于建造观测仪器的论述适逢其会。
从1417年起,兀鲁伯开始在撒马尔罕开设传授神学、教法、逻辑学、数学和自然科学的学堂,为此他希望邀请各个领域的顶尖学者前来主持。在这个研究机构里,卡西作为最杰出的天文和数学家而受到倚重。1424年,兀鲁伯的天文台破土动工,卡西继续被委任设计当时尺寸最大、测量最精确的仪器。
比起少年时期的坎坷,此时的卡西可谓已跻身成功人士之列。在回复仍留在卡尚的父亲的信件时,卡西生动地记载了他在撒马尔罕的生活,包括兀鲁伯这样的君主是如何频繁地光顾科研机构、他们的交往是多么密切,在与学院中其他六七十名学者辩驳或解决学术难题时他取得了多么辉煌的胜利,以及天文台的仪器是如何制作的等内容。兀鲁伯在很多方面都接纳了卡西的建议,可见他们二者之间紧密的合作关系。当然,这封信也成为研究帖木儿帝国科技史的重要资料。
卡西之兴与衰都与兀鲁伯有千丝万缕的联系。1429年6月22日,卡西在撒马尔罕天文台外遇刺身亡,年仅49岁。他暴亡的幕后凶手据说就是兀鲁伯,因为卡西对朝中另一派神学家持激烈的反对态度,这使得兀鲁伯不得不因平衡势力而忍痛割爱。不过,卡西追寻的科学事业并没有因他之死而中断,他未完成的著作在其身后仍被补充完善,兀鲁伯的天文台则一直维持运营到15世纪中叶。
测天之器
卡西在抵达撒马尔罕之前就开始在天文学领域作出贡献。1413年,他在赫拉特完成了《哈卡尼星表》,这部星表改进了一个半世纪前纳西尔丁·图西(详见本刊2018年11月《从“鹰巢”图书馆到大汗天文台——纳西尔丁·图西》一文)的《伊利汗星表》。卡西以六十进制的形式(卡西常用六十进制表示数值,但他对推广十进制也作出了许多努力),为每个角度求出分、秒以下4位(相当于十进制的小数点后8位)的精确数值,并制作表格帮助阅读者进行天球坐标系的转换(如从黄道坐标系变换为赤道坐标系)。这部书中还记载了河中地区许多地点的地理坐标,从而让绘制这一地区更精确的地图成为可能。
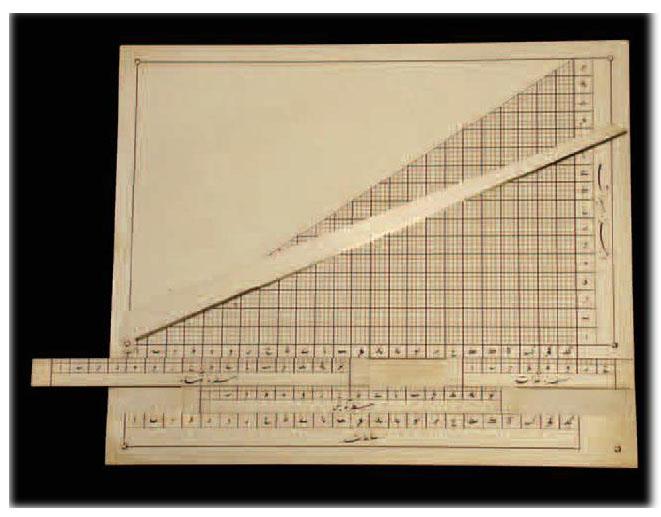
在天文仪器的发展历史上,卡西也占据着相当重要的地位。他首先研究了此前伊利汗国马拉盖天文台所使用的仪器,并在《喜悅花园》中描述了被他称为“联星盘”和“环带盘”的2种儀器。联星盘是10世纪早期发展出的行星定位仪的最终发展形态,其功能是在几乎不使用天文表的前提下,仅用机械方法就能给出行星在任意时间在黄道上的位置。卡西较前人作出的改进是在仪器中添置带有平行刻度尺的中央照准仪,在刻度尺的帮助下,观测操作可以方便地依靠观察照准仪的投影进行。环带盘则可以根据事先计算的每个行星的经度差,以及它们在各自轨道中每天穿越的距离,用机械计算2个行星相会合的日期。可惜的是,我们还不太了解这种计算仪器的其他细节。
一代算圣
卡西更大的成就在于数学,尤其是三角函数和代数领域。这方面他的代表作是1427年完成的《算术之钥》。这是一部内容如百科全书般丰富的数学著作,卡西希望通过运用“由相关已知量求得未知数的基本规则组成的科学”,也就是算术学,解决涉及天文学、测量学和社会经济生活等广泛领域内的问题,例如他以精湛的数学技能用复杂的计算方法和构造,计算出曲线外切体、斜圆柱体、斜锥形体、尖拱、拱顶、圆顶和钟乳石形体,以及其他不规则的空心体的体积,从而见证了在15世纪前半叶阿拉伯 伊斯兰文化区在数学上全面而专业的知识。
《算数之钥》中最显著的成就在于,卡西在书中借计算任意数字的五次方根,而总结出计算任意次方根的任意位小数结果的一般性方法,也就是西方数学所说的“霍纳法”。值得注意的是,卡西之前约200年,这种计算方法在中国南宋数学家秦九韶的《数书九章》中就得到运用。卡西利用构造五次方程求得数值解的思路,与秦九韶的方法有类似之处,这或许不能只用不谋而合概括,也许蒙古帝国向西的征伐裹挟着懂得这类算法的学者向西游历,让这种算法为伊斯兰学者所知。
我们熟知在探索圆周率精确数值的历史上,祖冲之曾让中国学者在各文明竞赛中一度领先,卡西则把祖冲之又大大甩到身后(当然他比祖冲之要晚约1000年之多)。在1424年完成的《圆周论》里,他批判了前人所使用的方法,而通过计算圆内接和外切3 × 228.即800335168边形的周长,给出了2倍圆周率(2π)精确到六十进制下9位之多的数值(其精确度相当于十进制下小数点后16位),即π≈3.14159265358979325。卡西在该书导言中提到,在宇宙那么大的尺度下,哪怕所用圆周率存在极小误差,也会导致实际观测中的显著错误。用他所提供的圆周率数值计算出的结果,能够让观测结果与预测值的误差在1根马毛(波斯长度单位,约等于寸的1/36)的宽度以内。这个结果比近200年后欧洲学者范·罗门给出的结果还要准确(但后者却常被称赞使圆周率测量进入了一个新的光辉时代)。
在未完成的著作《论弦与正弦》中,卡西计算出了从1°开始的精确到六十进制下10位的正弦值。此前学者们多依赖古典时期天文大师托勒密计算正弦的方法,在3°间隔下只能计算出个别角度的正弦值。卡西在计算方法上进行了创新,提出sin3θ=3sinθ4sin3θ。如果θ=1°时,就可以根据此前已知的3°正弦值计算出每隔1°的正弦数值。这样计算正弦数值就被转化为解三次方程。这种算法在西方通常被归功于16世纪法国数学家维耶特。卡西的计算结果让他贡献出空前精确的三角函数表,并对兀鲁伯此后推出精确的天文表格打下最关键的基础。
卡西在科学创造方面横空出世时,已经是20多岁的“大龄青年”,他在良好环境下全心投入研究,满打满算也只有10年时间。他的天文和数学成就,可以看出都是由细致耐心、孜孜不倦的科学精神一点一滴凝结而成的。他在仪器制作方面的创新,又体现出集成和发展前人成果的灵性。我们或许可以用“一代算圣”概括卡西的一生,同时惋惜如果不是在暗杀时猝然倒下,他本该作出多么大的贡献!
