轴向斜接管区域不连续应力的研究

2019-03-22王战辉曹保卫

榆林学院学报 2019年2期

王战辉，曹保卫

(榆林学院化学与化工学院，陕西榆林 719000)

随着石油化工、医药业、海洋工程、核能工业等技术的发展，压力容器成为化工、炼油、医药以及其他许多工业部门广泛使用的一种承压设备[1]。在工业生产中，由于其工作条件、用途不同、设备安装地点等不同，为了满足各种各样的设备连接不便的问题，衍生出各种各样的接管，由于接管的中心轴线和筒体中心轴线位置的不同，可以把接管分为径向接管、轴向斜接管和切向斜接管三种基本形式，其中使用最为广泛的是斜接管[2]。

由于斜接管的连接方式破坏了对称性，在其连接处的应力集中比垂直接管严重，使其成为了整个筒体的最薄弱部位[3]。虽然轴向斜接管在应力方面表现不佳，但是由于其自由度比较大，适应性强，能满足各种各样的管道和筒体的连接，仍然有着很大的优势。开孔接管不仅会引起筒体开孔接管边缘区域的应力集中；还会形成局部不连续区域，在边缘力和边缘力矩的共同影响下，产生不连续应力，促使局部区域应力增大，容易发生强度失效[4]。

轴向斜接管是压力管道和压力筒体中最重要也是受力情况最为复杂的承压部件，对压力管道及压力筒体的安全性和经济性有极其重要的影响，其变形情况和受力情况对压力管道和压力筒体中流体能否安全运输起着决定性的作用，所以对轴向斜接管进行不同结构参数的应力分析就显得尤为重要[5-7]。对于轴向斜接管的研究对于国内外来说是一项很重要的课题，因为这对其相关行业的安全生产起着很重要的作用[8]。笔者采用有限元分析方法，应用ANSYS软件平台通过建立内伸式开孔接管模型，实现压力容器轴向斜接管区域不连续应力的模拟分析，分析工作参数及结构参数对开孔接管区域不连续应力的影响规律。

1 有限元分析

1.1 工作条件及结构参数

图1 开孔接管1/4几何模型

图2 网格划分图

考虑轴向斜接管区域的几何对称性，选取开孔接管区的1/2建模，所建几何模型如图1所示。筒体和接管的材料均为45钢，弹性模量E为2.0×105MPa，泊松比μ为0.3。为了减小边缘应力的影响，选取圆柱壳长度L为1500mm，接管外伸长度L1为600mm，筒体轴线与接管轴线夹角θ=45°，筒体内径D为550mm，筒体壁厚t为6mm接管外径d为200mm，壁厚t1为10mm，内压p为1MPa。

1.2 网格划分

采用workbench里面自动划分网格(Automatic)的方法来对模型进行网格划分，所划分的网格由一个个等边三角形组成。网格划分的节点数为130000，网格划分的单元数为48000。网格划分图如图2所示。

1.3 边界条件及载荷

在分析中考虑设备的实际操作情况，忽略了重力、风载荷、温度载荷和地震载荷，主要考虑压力载荷。因为接管的长度足够长，远大于接管边缘的边缘应力衰减长度，所以在x方向可以不施加约束，只需考虑y和z方向的约束即可。

2 有限元模拟结果

通过改变斜接管与筒体中心线夹角、斜接管厚度、接管直径、接管连接处倒角五个参数，来考察其对轴向斜接管区域应力分布及其最大应力的影响，并对其进行应力强度评定。

2.1 轴向斜接管与筒体中心线夹角变化对最大应力的影响

图3轴向斜接管与筒体中心线夹角变化对应力分布的影响

改变斜接管与筒体中心线夹角，夹角变化对斜接管不连续区域应力分布的影响如图3所示。从该图可以看出，随着夹角的增大，最大应力呈减小的趋势，筒体与接管区的最大应力出现在圆柱形筒体和接管连接区域的锐角一侧。远离轴向斜接管区域，应力分布均匀，主要承受一次应力的影响，接管与筒体的连接区域，由于几何形状不连续会受边缘力和边缘力矩的约束，在边缘力和边缘力矩的约束下产生一次应力和二次应力，而远离接管区域，主要承受内压的作用，大小约等于薄膜应力；在斜接管附近区域，应力出现局部增大现象，接管局部区域就是典型的不连续区域，除了承受一次应力外，还承受二次应力的影响，因此会出现应力局部增大现象，是危险区域，容易发生强度破坏[9]。

图4轴向斜接管与筒体中心线夹角变化对最大应力的影响

其他因素不变，改变轴向斜接管与筒体中心线夹角，夹角变化对最大应力的影响如图4所示，可以看出，当轴向斜接管与筒体中心线夹角为30°、45°、60°、75°、90°时，最大应力为315.47MPa、197.83MPa、127.13MPa、114.19MPa、113.8MPa。夹角增大，最大应力随之减小：当夹角小于45°时，最大应力减小幅度大，当夹角超过45°时，最大应力基本维持不变。这是由于夹角越小，接管与筒体几何形状不连续现象越严重，边缘力和边缘力矩越大，相对应产生的最大应力越大。由此可得出，轴向斜接管与筒体最大应力随着夹角的增大而减小。

2.2 轴向斜接管厚度变化对最大应力的影响

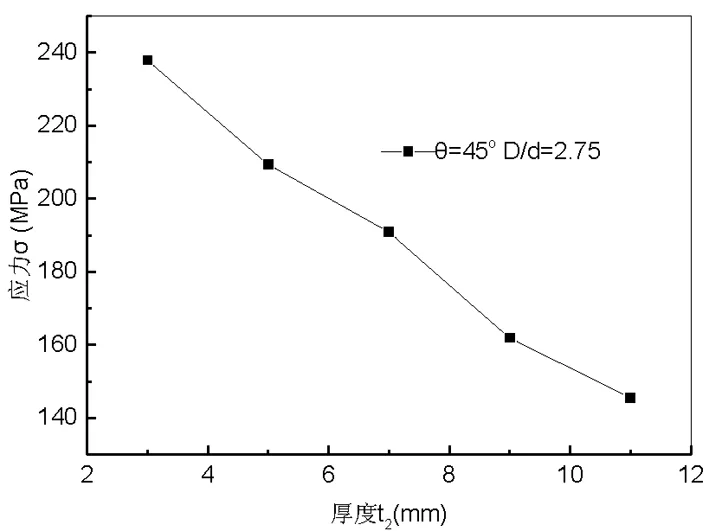
图5 轴向斜接管厚度变化对最大应力的影响

其他因素不变，改变轴向斜接管厚度，斜接管厚度变化对最大应力的影响如图5所示，可以看出，当斜接管壁厚为3mm、5mm、7mm、9mm、11mm时，最大应力为237.95MPa、209.45MPa、190.94MPa、161.95MPa、145.56MPa。斜接管壁厚增大，最大应力随之减小：最大应力与壁厚基本呈线性的关系。这是由于一方面，接管壁厚越大，强度刚度越好，承压能力越大，对于相同的压力，最大应力小，越不容易失效；另一方面，接管壁厚大，开孔系数减小，开孔对筒体的削弱程度减小，应力集中系数减小，最大应力也随之减小[10]。由此可得出，轴向斜接管与筒体最大应力随着接管厚度的增大而减小。

2.3 轴向斜接管内半径对最大应力的影响

图6 轴向斜接管内半径对最大应力的影响

其他因素不变，改变轴向斜接管内半径，轴向斜接管内半径变化对最大应力的影响如图6所示，可以看出，当斜接管壁厚为350mm、300mm、250mm、200mm、150mm时，最大应力为254.46MPa、237.77MPa、218.18MPa、174.61MPa、129.6MPa。斜接管内半径增大，最大应力随之增大。这是由于接管半径增大，开孔系数增大，在其他因素不变的情况下，不连续区域应力集中系数增大；另一方面，半径增大，开孔接管附近区域边缘力和边缘力矩增大，由此引起的不连续应力随之增大，容易发生强度失效。由此可得出，轴向斜接管与筒体最大应力随着接管轴向斜接管内半径的增大而增大。

2.4 筒体与轴向斜接管连接处圆角值对最大应力的影响

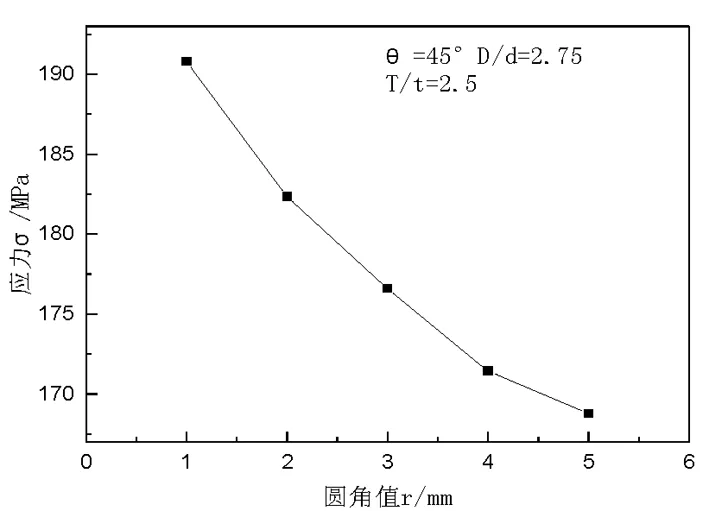
图7筒体与轴向斜接管连接处圆角值对最大应力的影响

其他因素不变，改变筒体与轴向斜接管连接处圆角值，圆角值的变化对最大应力的影响如图7所示，可以看出，当圆角为1mm、2mm、3mm、4mm、5mm时的最大应力为190.8MPa、182.37MPa、176.6MPa、177.45MPa、168.791MPa。圆角值增大，最大应力随之减小。可以看出，圆角的引入能改善轴向斜接管附近不连续区域应力分布情况，对于最大应力的减小能起到很好的缓冲作用，圆角能改善接管与筒体的连接处的应力集中现象，在一定范围内，圆角越大，最大应力越小，容器越安全，不容易发生强度破坏，但是圆角太大，制造困难。由此可得出，轴向斜接管与筒体最大应力随着筒体与轴向斜接管连接处圆角值的增大而减小。

2.5 应力评定

根据JB4732《钢制压力容器—分析设计标准》的要求，针对压力容器不同部位处按应力的性质、作用范围及分布情况等可分为以下三类：一次应力(P)、二次应力(Q)和峰值应力(F)，而一次应力(P)又可分为一次总体薄膜应力(Pm)、一次弯曲应力(Pb)和一次局部薄膜应力(PL)[11]。对于不同的应力根据不同的准则进行应力强度评定：

1、一次总体薄膜应力强度：Pm≤1.5Sm；

2、二次应力强度：PL +Pb +Q≤3 Sm式中：

Sm：为材料的许用应力强度，MPa。

应力评定方法分为点处理法、线处理法和面处理法。采用线处理法，对开孔接管最大应力处进行应力评定，选择三条路径进行应力评定：1-1、沿接管厚度；2-2、沿壳体厚度、3-3沿相贯线厚度最大处。

应力评定结果如表1所示：

表1 应力评定结果

从表1中的应力评定结果可以看出，最大应力处三条路径均能满足强度要求，不需要进行补强。圆柱体开孔接管处由于几何形状发生突变而产生不连续现象，产生边缘力和边缘力矩，从而产生一次应力、二次应力等，应力最大，最容易出现强度失效，因此次部分的尺寸和结构至关重要。可以考虑增加圆角、局部厚度增加或者其他过渡形式减少此处的应力。