基于灰度关联-极限学习机的土壤有机质含量高光谱多尺度反演

叶红云，熊黑钢，包青岭，王 宁，马利芳

（1.新疆大学资源与环境科学学院/教育部绿洲生态重点实验室，新疆乌鲁木齐 830046；2.北京联合大学应用文理学院城市系，北京 100083）

土壤有机质（SOM）主要由各种动植物的残体、微生物体及其分解和合成的各种有机物质组成，虽然其含量仅占土壤总量的很小一部分，但在土壤肥力上的作用却十分重要。不同土壤类型和区域由于气候以及人类干扰程度的不同，使得有机质分解程度不同，其光谱反射特性也存在差异。近年来，利用高光谱对土壤有机质进行估测研究因其便利性而被普遍使用［1-3］。但土壤高光谱曲线是土壤属性的综合体现，存在很多与有机质无关的噪声，且信息相关性强、信息冗余等，因此对于高光谱噪声的去除成为近年来研究的热点［4-6］。目前光谱去噪方法有很多，如Savitzky-Golay平滑去噪、移动平均法、傅里叶变换（FFT）滤波等，但这些方法能检测的信噪比信息有限。小波变换近几十年来在高光谱遥感领域以其在信号去噪和数据压缩方面独特的优势为地物光谱信息提取提供了新途径［7-9］。但目前的研究大都以人类干扰的土壤为对象，且均是有机质含量较高的地区，未充分考虑到人类干扰程度不同且有机质含量较低时光谱的估测情况。灰钙土是新疆北部典型的土壤类型之一，其有机质质量分数大多低于2%。研究表明，有机质含量较低会减弱其光谱反射率的吸收特性［10-11］，导致在估测有机质含量时存在光谱响应较弱、模型预测精度较低等问题，因此有必要探究进一步提高预测精度的方法。

灰度关联法是分析各因素之间关联程度的方法，在光谱分析中可以很好地识别敏感波段，有利于优化模型精度［12］。极限学习机（ELM）算法可随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需设置隐含层神经元的数量，便可获得唯一的最优解，与传统的BP神经网络算法相比，ELM方法学习速度快、泛化性能好［13］。虽然目前这2种方法应用较多，但将二者结合应用于干旱区小波变换最佳光谱层的确定中还未见报道。

本研究从人类干扰程度出发，结合植被特征、土地利用方式等指标，将研究区划分为轻度、中度和重度干扰区3种干扰类型，采用离散小波技术从土壤光谱数据中分别提取有机质信息，并利用相关分析和灰色关联分析法挑选有机质含量的敏感波段，结合极限学习机构建估测土壤有机质含量的模型，以期提高估测精度，为精准农业的发展提供借鉴和科学依据。

1 材料与方法

1.1 研究区概况

研究区位于新疆北部的阜康市（87°44′～88°46′E，43°29′～45°45′N）。地势南高北低，平均海拔为452 m。气候为典型的温带大陆性气候，夏季高温，冬季严寒，光能资源充足，热量资源丰富，降水稀少且空间分布不均，年降水量为163 mm，年蒸发潜力为2 000 mm左右［14］。

本试验将研究区分为Ⅰ、Ⅱ、Ⅲ3个区。Ⅰ区为轻度干扰区，因距离人类居住地较远，并未开发利用，该区人类活动很少，偶有人类进入，基本保持了其原有风貌；Ⅱ区为中度干扰区，处于新疆生产建设兵团102团附近，大部分为废弃耕地，人类目前对其干扰较小；Ⅲ区为重度干扰区，位于研究区的西南部，人类对其开发利用程度较大，主要开发利用方式为林地（包括人工梭梭林地、榆树林地、育苗地），尚处于开发利用的初期阶段（表1）。

参照余作岳提出的人类干扰分类体系［15］，研究中的Ⅰ区长期以来的主导干扰因子只是人类偶尔进入该区，并未对该区原有植被类型造成干扰，即几乎不引起土壤中组分的变化，属于无效干扰；而Ⅱ区、Ⅲ区经过人类开垦、植树等干扰活动后，使得植被类型发生改变，正常演替序列被打破，土壤中的盐分、有机质等组分也随之发生变化，即表1中的3种干扰改变了生态系统的正常动态发展，属于有效干扰。因此可以用轻度干扰区的各项指标作为对照来比较分析中度干扰、重度干扰区土壤有机质含量的变化等信息。

表1 研究区3类典型干扰区基本情况

1.2 实地调查与采样

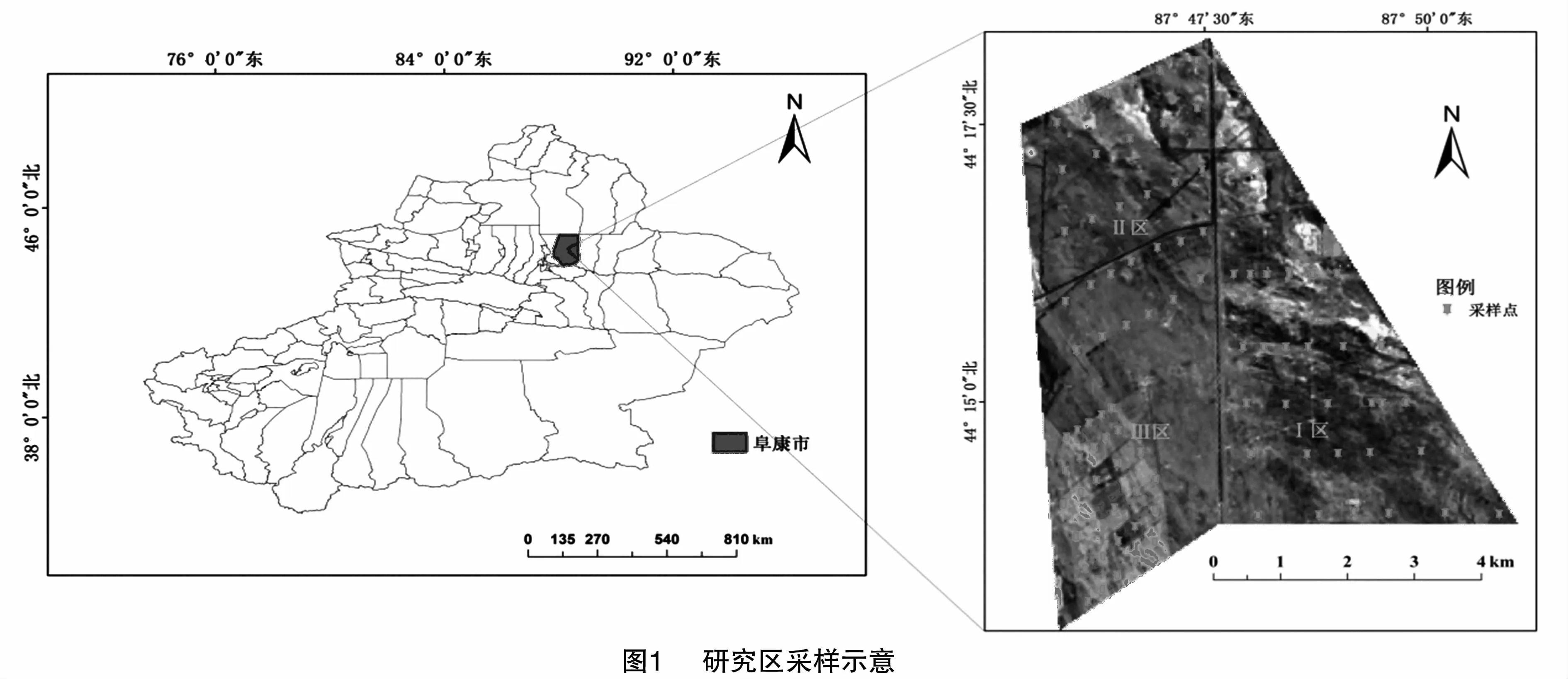
本研究于2017年10月进行了土壤样本数据采集。在Ⅰ区由南向北布设5条间距500～700 m的东西向采样线，每条采样线布设6个采样点；Ⅱ区按同样方向布设5条间距400～600 m的采样线，每条采样线上选择5～7个具有代表性的的采样点；Ⅲ区面积较小，因此布设6条间距200～400 m的采样线，每条采样线布设5个采样点。每个区均为30个采样点，由此构成由90个采样点组成的空间网格，并分别对其进行GPS（全球定位系统）定位。采样点具体分布见图1。本次野外数据采集主要包括以下2个部分：

1.2.1 野外土壤高光谱数据的采集 光谱测量采用美国ASD公司生产的便携式FieldSpec®3Hi-Res光谱仪，波段为350～2 500 nm，350～1 000 nm光谱采样间隔为1.4 nm，光谱分辨率为3 nm；1 001～2 500 nm范围内光谱采样间隔为1.1 nm，光谱分辨率为8 nm。由于本试验光谱测量采用野外实测方法，为了减少太阳高度对光谱采集造成的不利影响，试验均选在当地时间11：00—15：00、晴朗少云、无风的天气进行。每次采集光谱前对光谱仪进行白板校正以去除暗电流的影响。采用25°视场角探头，且距采样地面15 cm处垂直角度，在每个采样点按梅花桩对表层土壤原始光谱进行采集，每个位置重复测量10次，得到的50条光谱曲线的平均值即为该采样点的实测光谱值，共测定90个样点的采样光谱曲线。野外测量时观察每个样点的实测光谱值，将出现异常的光谱曲线删除并重新测定，以便获得更加准确的实测光谱反射率。

1.2.2 土壤有机质含量的采集 土样的采集与高光谱数据的测定同时、同地进行，选择地势平坦、能代表样点周围区域特征的地点作为采样单元，每个采样点分别从周边1 m范围内不同的地点挖取3个0～10 cm的土坑分别采样，并混合均匀放入密封袋中，封口标记编号，用手持GPS定位后记录经纬度。将采集的样品带回实验室经自然风干、去除杂质后，研磨过1 mm筛，送至中国科学院新疆生态与地理研究所，由专业人士采用重铬酸钾容量-外加热法测定［16］有机质含量。

1.3 高光谱数据处理

因为光谱仪器波谱两端的边缘波段存在较大的仪器噪声，首先剔除350～399 nm和2 451～2 500 nm波段。然后运用OriginPro 9.0对光谱反射率进行Savitaky-Golay（9点）平滑去噪处理。通过观察研究区90个采样点的土壤光谱曲线，发现野外实测光谱在1 350～1 450 nm和1 830～1 950 nm附近出现异常，这主要受到水分吸收带和大气的影响，因此将其剔除。

1.4 离散小波变换

离散小波变换是基于傅里叶变换发展起来的数据分析方法，可以将原始信号按照不同的尺度、频率进行多级分解，得到不同分解尺度下的小波系数。通过小波系数可以实现原始光谱的信息重构。借鉴前人研究结果［17-18］，本研究对原始光谱进行1～8层小波分解并重构各层光谱进行分析。

1.5 灰色关联度分析

灰色关联分析是通过灰色关联度来揭示2个因素的贴近程度，曲线几何形状越接近，灰色关联度越大。一般而言，若关联度≥0.8，则2个因素贴近程度很好；若关联度介于0.6与0.8之间，则贴近程度较好；若关联度小于0.5时，则认为基本不相关［19-20］。

1.6 极限学习机（ELM）

ELM是发展于单隐含层前馈神经网络的新型神经网络算法［21］。在算法执行过程中随机设定输入层与隐含层之间的权值和阈值，无需反复调整迭代网络的输入权值及隐元的偏置，并且产生唯一的最优解，避免陷入局部最优解的情况，因此具有学习速度快和强泛化性的优点［22］。

1.7 模型的建立与检验

模型的精度检验主要通过判定系数（coefficient of determination，简称R2）、均方根误差（rootmean square error of calibration，简称RMSE）和相对分析误差（residual prediction deviation，简称RPD）来检验实测值和估测值的拟合效果。R2越大，RMSE越小，说明模型精度越高［23］。Viscarra等对模型RPD做了如下分类，RPD＜1.0，预测能力极差；1.0＜RPD＜1.4，预测能力较差；1.4＜RPD＜1.8，预测能力一般；1.8＜RPD＜2.0，预测能力较好；2.0＜RPD＜2.5，说明预测能力极好［24］。

2 结果与分析

2.1 土壤有机质含量统计特征

选用SPXY（光谱-理化值共生距离）算法［25］分别计算出Ⅰ、Ⅱ、Ⅲ区各个样品有机质含量之间的欧式距离，按照3∶2的比例划分为建模集和检验集。研究区土壤有机质含量总体较低，且随着干扰强度的减少，经营方式逐渐回归自然状态，有机质含量逐渐增加，变异系数逐渐减少（表2）。这是因为Ⅰ区原始植被状态保存得完好，主要分布有梭梭、柽柳、猪毛菜、盐爪爪等，植被覆盖度较高；而Ⅲ区受人类活动干扰的影响，土地利用方式多样，主要有人工林、枸杞育苗地以及其他农业土地利用类型，使得空间异质性与其他2个区相比加强，变异系数也增加。

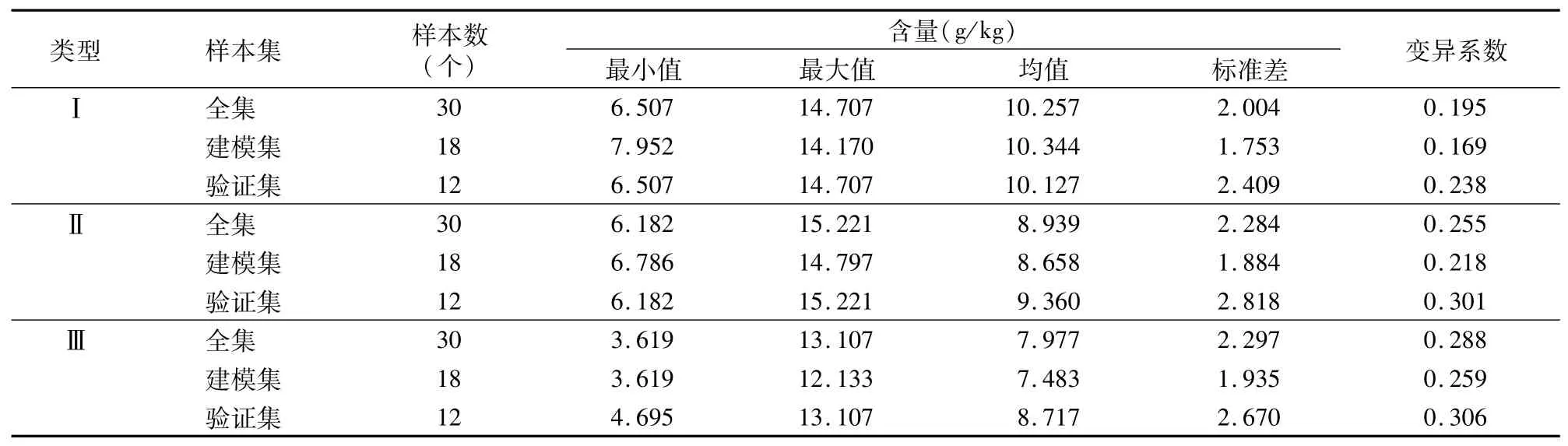
表2 土壤有机质含量的描述统计量

2.2 不同程度人类干扰下原始光谱反射率的小波变换分析

应用小波分解与重构去噪方法需要对各种光谱信号进行分解以选择分解层次，从而在重构时达到去噪与保留细微光谱特征的平衡点。在MATLAB R2017b中选取常用的db4函数作为小波母函数，并对原始高光谱数据进行8层离散小波分解，然后将分解后的每层小波系数分别进行光谱重构（图2）。随着分解层数的增加，吸收谷由较为“尖锐”逐渐变得“圆润”。与L0相比，L1、L2的光谱反射率曲线变化不大，而L3～L5则凸显了光谱曲线的局部细节，使得波峰、波谷更加清晰，到L6、L7光谱反射率趋于平滑，L8则几乎看不到吸收谷。表明适当的分解尺度可以减少背景和噪音的影响，但分解尺度过高可能会导致某些有效光谱信息的丢失。Ⅰ区、Ⅱ区、Ⅲ区的光谱反射率曲线形态大致相同，土壤高光谱反射率曲线呈现Ⅰ区＜Ⅱ区＜Ⅲ区，即随着人类干扰程度的增加，土壤高光谱反射率增强。

2.3 不同程度人类干扰下SOM与重构光谱的相关性分析

以0.05显著性水平为阈值，通过对比不同分解层数与土壤有机质含量的相关性来选择适宜的分解层（表3）。随着分解层的增加，Ⅰ区、Ⅱ区、Ⅲ区通过0.05显著性水平检验的相关系数逐渐减小，在L6附近变化程度不大，且通过检验的敏感波段数均在L6处达到最高值，分别为405、198、167个，而L7、L8的敏感波段数量则呈现快速下降的状态。表明分解层数的增加，在一定程度上使得小波系数输出原始光谱信息的能力逐渐减弱。因此，本研究选取相关性较强且通过的敏感波段数量较多的前6层特征光谱用于土壤有机质含量模型的反演研究。

2.4 各层敏感波段的选取

基于以上分析，将通过0.05水平检验的原始光谱（L0）和小波分解后（L1～L6）的特征光谱分别进行1/R、lg R、R′、（1/R）′、（lg R）′等5种数学变换，以获得各分解层的敏感波段。由于高光谱数据量较大，且通过小波变换后信息含量更大，使得选择敏感波段难度加大，因此本研究以通过0.05显著性水平以及相关性最大的原则选择每层的敏感波段（表4）。总体来看，Ⅰ区敏感波段主要分布在可见光区（752～875 nm）和近红外区（1 820 nm），Ⅱ区相关性最大的波段主要集中在可见光区（400～600 nm），而Ⅲ区主要集中在近红外区（1 200～1 300 nm）；从不同数学变换来看，无论是哪个区，微分变换后整体上相关系数均有所增加；对于不同分解层来说，Ⅰ区、Ⅱ区、Ⅲ区相关系数较高的波段均主要集中在L3和L4层，以Ⅰ区的1/R为例，L4层相关系数最高，为0.498 3，比L0处的相关系数提高了0.05左右，说明微分处理可以将可见光区微弱的有效信息放大，有利于敏感波段的选择。

2.5 特征光谱变换与SOM灰色关联度分析

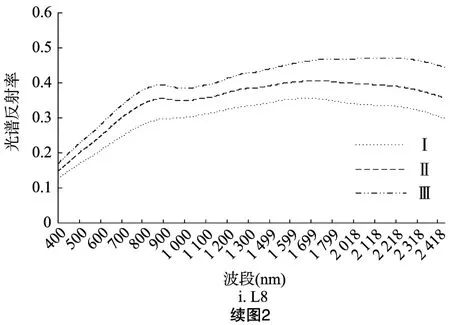
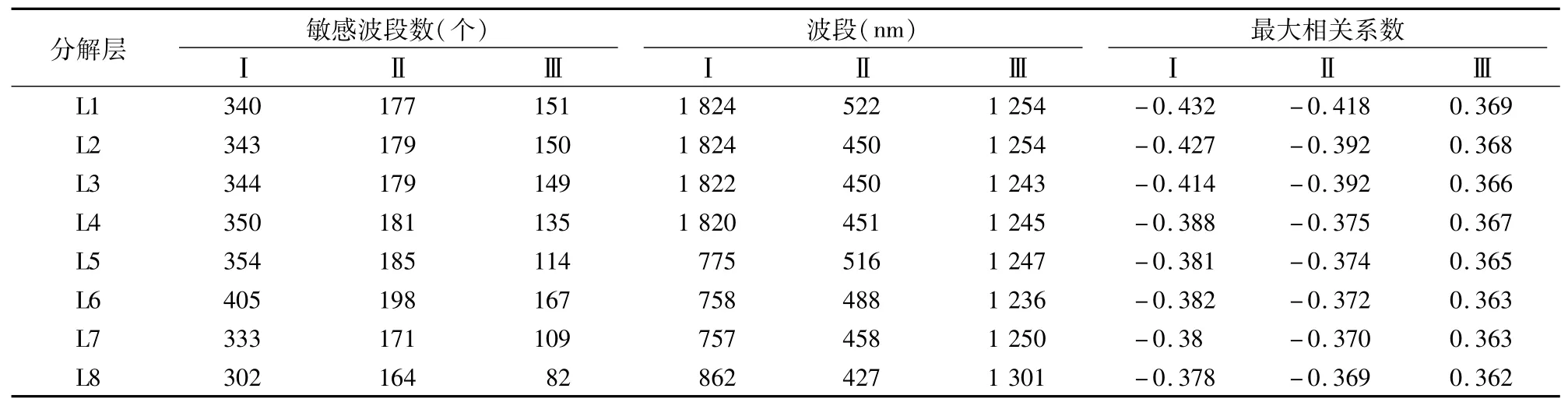
表3 不同程度人类干扰下SOM 与各层敏感光谱的相关性分析

表4 SOM 与各层特征光谱的不同数学变换的最大相关性及波段所处位置

单纯依赖简单的相关性分析确定敏感波段并不能完全确定有机质含量的有效信息，具有一定的局限性。为了进一步衡量不同分解层所选的敏感波段与有机质的关联程度，更好地筛选出表征有机质的敏感光谱指标因素，本研究对其进行了灰色关联分析（表5）。总体来看，Ⅰ区、Ⅱ区和Ⅲ区各层特征光谱及其不同数学变换与有机质含量的灰色关联度均高于小波变换前（L0）所对应的数据，表明小波变换在去除噪声的同时也最大程度地保留了光谱中的有效信息，使得小波变换的各层重构光谱与有机质含量的关联程度增加。从同一分解层来看，经过微分处理后小波变换重构特征光谱与有机质含量之间的灰色关联度总体上均高于对应的未经微分处理的数学变换，如Ⅰ区L0，其关联度排序依次是（1/R）′＞R′＞（lg R）′＞1/R＞lg R＞R，进一步说明在小波去噪的基础上，通过微分数学变换可以显著增强光谱曲线上局部位置对有机质含量变化的响应差异。

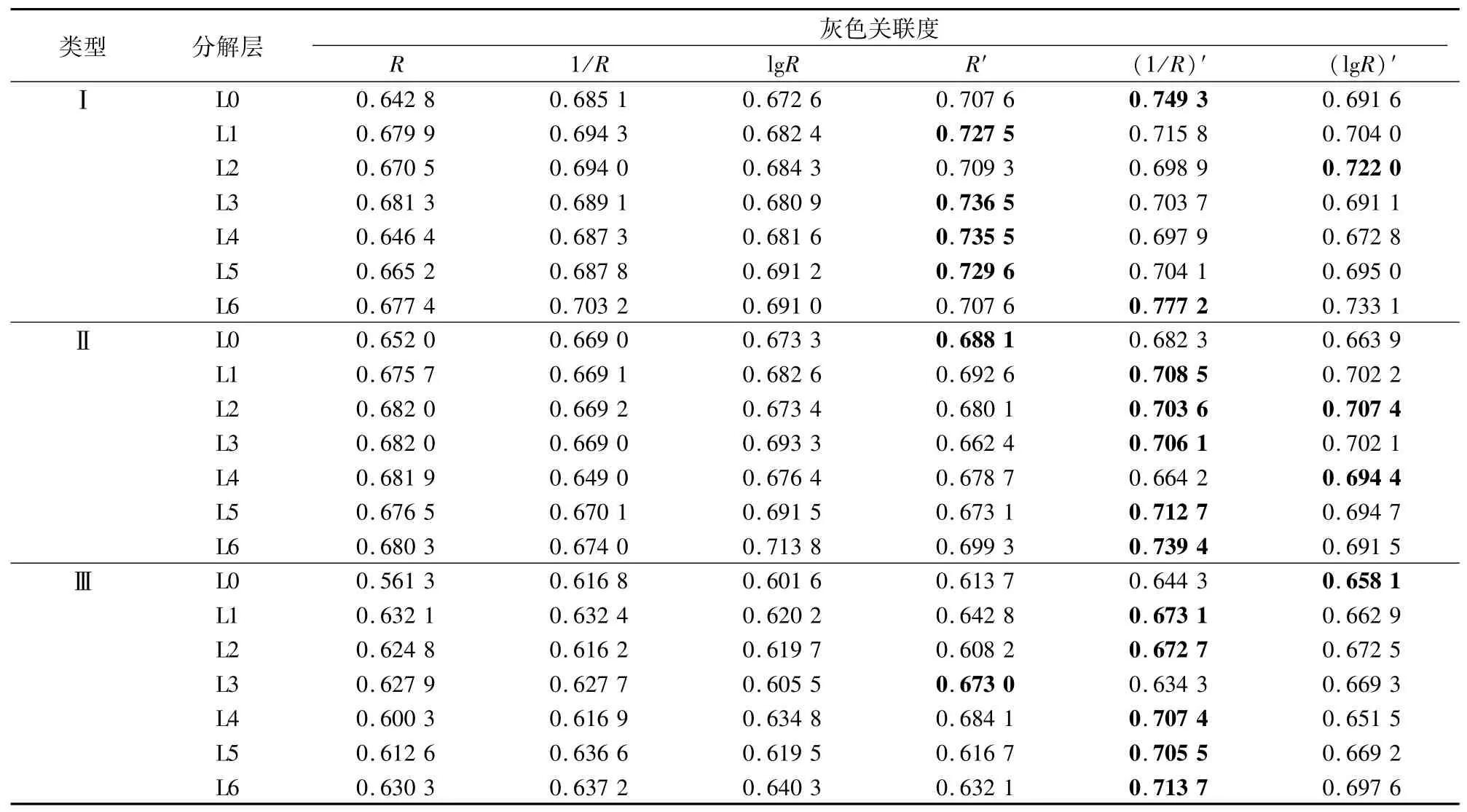
表5 不同程度人类干扰下各层特征光谱不同数学变换的灰色关联度

2.6 SOM反演模型的优选

分别选取Ⅰ区、Ⅱ区和Ⅲ区的原始光谱和重构光谱及5种数学变换后与有机质含量相关系数最大的波段为自变量、土壤有机质含量为因变量，结合PLSR和ELM算法构建有机质含量的估测模型，通过对比得出灰度关联-极限学习机模型建模精度均优于对应的相关系数-PLSR模型，由于各层小波重构光谱所建立的模型太多，此处仅对各层灰色关联-ELM模型进行讨论。此外，由于小波变换把原始光谱分解成不同的离散光谱，每层光谱均表征了原始光谱中的特定信息，如果单一地选择某一层重构特征光谱建模，容易导致其他分解层中有效信息的丢失，使得所选变量不能完全反映有机质含量信息，对建模精度产生影响。因此，本研究再以各层相关系数最大的波段组合以及灰色关联度分析所选的波段组合，分别建立PLSR和ELM模型。仅列出利用相关系数最大波段组合所建的PLSR模型和灰度关联所建立的ELM模型，分别用L-R、L-GRD表示（表6）。

从各分解层的建模效果来看，以L3、L4所构建的模型最优。以Ⅰ区为例，前4层构建的验证集模型R2呈不同程度的增加，到L4模型R2最优（0.807），均方根误差最小（1.093 g/kg），且RPD大于2（2.109），表明第4层能够极好地预测有机质含量。此后，随着分解层数的增加，各模型的R2降低，RMSE增大，RPD也随之减小。这与王延仓等的研究结果［17，26］一致，即利用小波重构原始光谱时，随着分解层数的增加，使得原始光谱中噪声和信号信息更加明显，有利于有效光谱信息和噪声的分离。但分解尺度过大，会导致有效信息的丢失而使得模型误差较大。从总的建模效果来看，对于Ⅰ、Ⅱ、Ⅲ区利用相关分析-偏最小二乘法所建模型验证集决定系数R2分别为0.568、0.517、0.544，RMSE分别为1.620、1.771、3.208，RPD均小于1.4，预测能力较差。而利用灰度关联-极限学习机建模效果均最好。以验证集所建模型为例，与原始光谱所建模型相比，Ⅰ、Ⅱ、Ⅲ区R2分别提高了9.8%、8.9%、13.6%，RMSE分别减少了18.3%、2.5%、7.3%，RPD分别增大了39.9%、22.2%、46.4%，这可能是因为单一地利用某一层的小波重构光谱，并不能完全将光谱中的细节体现出来，通过灰色关联度分析将不同层的特征光谱组合起来，可以很好地体现每一层特征光谱与有机质含量的关系，增加了模型的稳定性和模型精度。同时，灰色算法结合光谱和有机质信息，能够较好地挑选敏感波段，且ELM算法是在BP神经网络基础上的优化新型算法，具有学习速度快且泛化性能好的优点。

此外，Ⅰ区不同分解层下的土壤有机质建模精度均高于相应的Ⅱ区、Ⅲ区，这主要是因为Ⅰ区为轻度干扰区，基本保持原有状态，有机质分布较为均质，而Ⅱ区、Ⅲ区由于受到人类不同干扰程度的影响，不同地块的土地利用方式不同，使得有机质含量分布变异性较大，导致模型预测精度相对较低。

3 结论

对于人类不同干扰程度土壤的小波重构光谱来说，对其最大的影响因素主要是有机质含量的高低，整体上随着人类干扰程度的增加，小波分解的重构光谱反射率随之升高，排序为Ⅰ区＜Ⅱ区＜Ⅲ区。

在确定最佳分解尺度中，Ⅰ区、Ⅱ区、Ⅲ区土壤有机质和重构光谱通过0.05显著性水平检验的敏感波段在L6处变化幅度不大，且通过检验的敏感波段数达到最大值，分别达405、198、167个。因此L6为本研究的最大分解层。

对于不同层的重构光谱来说，小波分解使得重构光谱及各种数学变换与有机质含量之间的相关性和灰色关联度有不同程度的提高；对于同一分解层来说，经过微分变换后与有机质含量之间的相关性和灰色关联度均优于微分变换前，表明小波变换和微分结合有利于挖掘光谱中的有效信息，提升其与有机质含量的相关性。

表6 土壤有机质含量反演最优模型的建模集与验证集结果

对3个区原始光谱分别进行不同尺度的分解后（L1～L6），总体上L3、L4的建模效果最好，与L0建模效果相比，验证集R2分别提高了0.06、0.04、0.05，表明L3、L4在去噪的同时又最大程度上保留了光谱的有效信息。

不论在哪个区，利用灰度关联与ELM结合均优于传统建模方法，且Ⅰ区、Ⅱ区、Ⅲ区均以L-GRA所建模型的精度最高。其验证集R2均大于0.73，RPD均大于2，相比原始L0所建模型，RPD分别提高了0.679、0.400、0.678。预测能力由较差上升为极好，表明灰色关联-极限学习机方法有利于最大程度地筛选有机质敏感光谱信息，尤其适用于干旱区有机质含量较低情况下有机质含量的预测，且不受人类干扰程度的影响，是估算干旱区有机质含量的优选模型。