基于合成孔径聚焦成像的超声衍射时差法图像优化处理

，，

(绍兴市特种设备检测院，绍兴 312071)

作为新技术之一的超声衍射时差法(TOFD)与传统的超声波检测法不同，TOFD是一种依靠被测试件内部缺陷的端角和端点处得到的超声波衍射能量来对缺陷测深、定高的方法，缺陷定位不依靠信号振幅，具有可靠性好、定量精度高、信息量丰富、检测效率高等优点[1-2]。TOFD技术的这些优点特别适合对焊缝缺陷的尺寸、位置、形状等信息进行精确量化，但由于TOFD探头覆盖范围广，声束指向性较差，缺陷在图像上常呈抛物线形，横向分辨率存在不足[3-4]。合成孔径聚焦技术(SAFT)最先用于合成孔径雷达，其可以用低指向性的信号源和较低的工作频率来获得较高的方位分辨率[5]。超声检测领域用SAFT来提高超声图像的分辨率，如医学上血管内超声成像[6-7]、焊缝高分辨率的超声重建图像以及相控阵图像的重建等[8-9]。在国内，也有许多学者[10-13]对TOFD图像的SAFT重建进行了研究，有助于提高TOFD图像的缺陷横向分辨率，实现对距离较远缺陷的准确定位和定量评估。为了改善SAFT在TOFD领域的应用效果，提高TOFD图像质量，从SAFT算法的原理出发，采用维纳滤波、匹配滤波、时移差值等方法对原始信号噪声和相位混叠进行抑制，显著提高了SAFT的处理效果，得到了较好的缺陷图像分辨率。

1 SAFT成像算法原理

超声领域的SAFT是根据各成像点的空间位置，对接收到的散射信号作适当的声时延迟或相位延迟后再合成得到的逐点聚焦成像[14]，SAFT的方位分辨率只与超声波激发晶片的尺寸有关，与声波频率和声程无关，通过SAFT可以使超声图像横向分辨率提高到探头晶片尺寸的一半[15]。TOFD非平行扫查时合成孔径聚焦成像原理示意如图1所示，一组TOFD探头以速度v在焊缝两侧进行非平行扫查(D扫)，超声波速度为c，缺陷O处的深度为h，经过时间t后探头从AA′移动到BB′，假设接收到缺陷衍射波A扫信号的时间分别为tA、tB，探头中心间距(PCS)为2S，由几何位置关系可得

(1)

式中：Δt为接收到缺陷波信号的时间延时；L=vt，为探头移动的距离；H为缺陷深度。

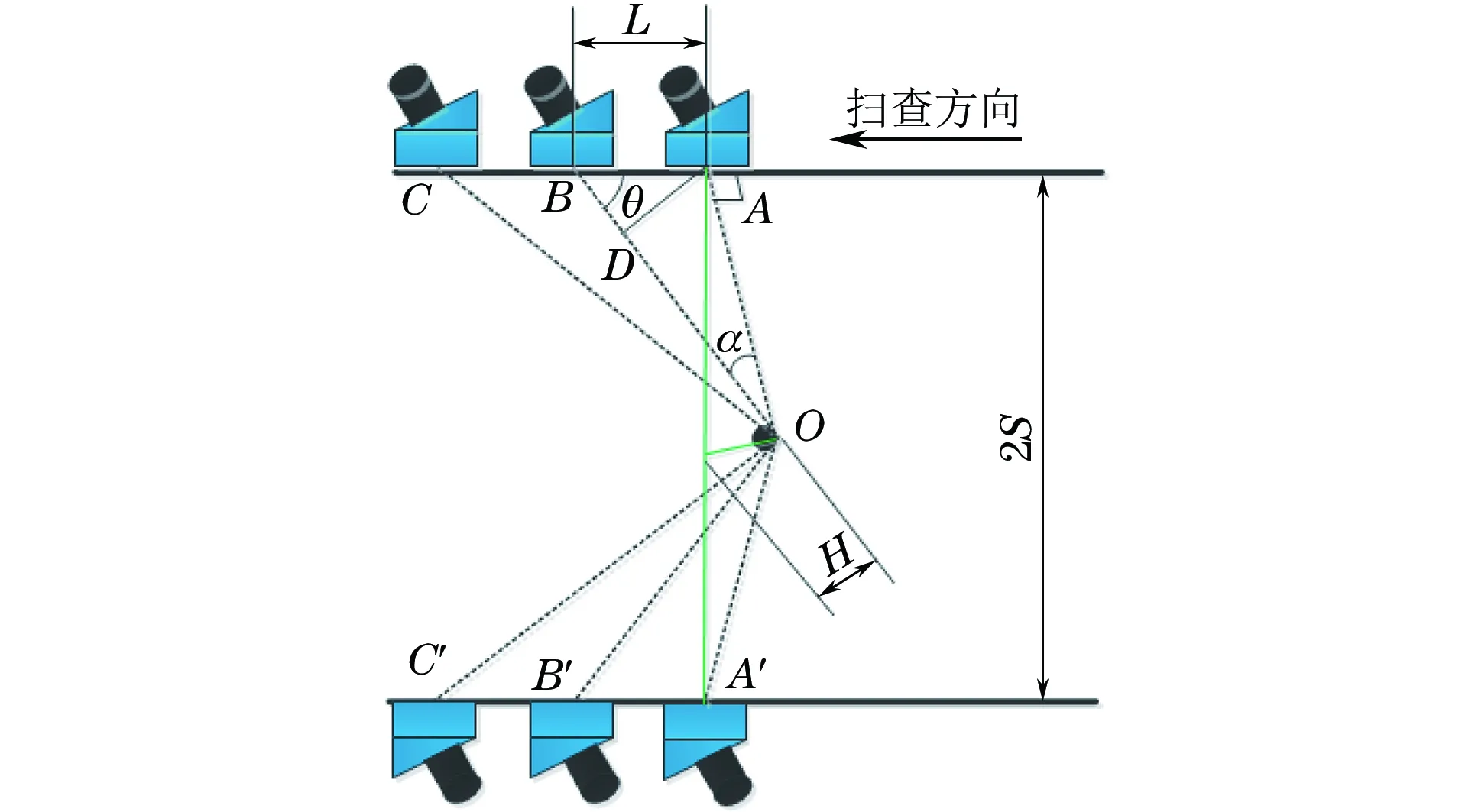
图1 TOFD非平行扫查时合成孔径聚焦成像原理示意

在TOFD检测中，A扫信号在扫查方向上与扫查分辨率ΔL相对应，因此探头移动距离L可用nΔL来代替；TOFD图像中沿扫查方向第i个A扫信号中，第j个AD采样数据点相对应的像素点记为Ai(xi,tj)，xi为扫查距离，tj为接收到当前数据点的时间。假设图1中TOFD探头在AA′位置时，TOFD图像中代表缺陷O的图像点为Ai(xi,tj)，则缺陷O距离上表面的深度Hj可表示为

(2)

在式(1)中利用nΔL替代L，Hj替代H，则式(1)可改写为

(3)

同理，在平行扫查(B扫)时，将TOFD探头中心点移动nΔL距离时，探头接收到缺陷O散射的A扫信号的时间延时可表示为

(4)

根据时间延时Δtnj对Ai(xi,tj)进行时运算，假设参与合成孔径运算的数据点数为2N+1，则TOFD图像中Ai(xi,tj)点的合成孔径表达式为

(5)

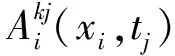
2 TOFD图像的信号处理及SAFT算法实现

2.1 SAFT的时移线性插值

SAFT超声成像需要对一组邻近的A扫信号进行时移运算，如式(5)所示，假设超声系统的A/D采样周期为ΔT，记tj-Δtnj为(I+α)ΔT，其中I为整数，α为小数，可以看出，当α不为零时，Ai+n(xi+n,tj-Δtnj)代表的点落在两个相邻像素点之间，常规的方法是在IΔT和(I+1)ΔT之间取距离最近的点，这样不可避免地造成一定的时移误差。为了提高时移运算的精度，对延时时移进行线性插值处理，如式(6)所示。

Ai+n(xi+n,tj-Δtnj)=Ai+n(xi+n,IΔT)+

α{Ai+n[xi+n,(I+1)ΔT]-Ai+n(xi+n,IΔT)}

(6)

2.2 SAFT的匹配滤波

在TOFD检测时，随着探头的连续移动，接收探头接收到的缺陷散射信号的时间序列发生延时，而且其相位和频率也会变化，这种现象可以用多普勒频移来解释。假设探头入射波信号为连续信号A(x,t)

(7)

式中：A为信号幅度；λ为波长。

则图1中探头在BB′位置接收到的缺陷散射信号为

A(x,t)=CsAexp(i2πct/λ)×

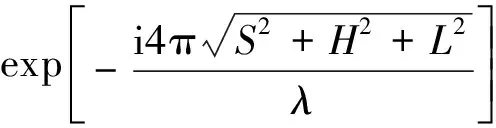
(8)

式中：Cs为入射声束在O点的散射系数。

(9)

把式(9)代入式(8)可得

(10)

O点的散射信号的相位与(nΔL)2呈线性变化，这即是多普勒频移，可以看出,SAFT成像时如果仅进行时移运算而不考虑相位变化，在下一步进行聚焦求和运算时会造成相位混淆或干扰，引起图像方位分辨率的下降，因此为了提高SAFT成像品质，必须要对此相位变化项进行滤波处理。匹配滤波器是最佳线性滤波器的一种，以输出信噪比最大为准侧，其传递函数是输入信号的复共轭，滤波过程可以理解为求自相关，可以抵消各频率成分的相位，与式(10)中相位变化项对应的匹配滤波器的冲击响应为

(11)

匹配滤波器对信号的处理可以在时域做卷积运算,也可变换到频域作乘法运算，时域方法通常用于信号采样频率不高、滤波器系数点较少的情况，利用卷积运算来实现。在TOFD图像的距离方向上对参与合成孔径运算的2N+1个A扫信号进行匹配滤波，考虑到参与运算的A扫信号数量较少，选用时域卷积算法，如式(12)所示

(12)

对于B扫，TOFD探头垂直于焊缝方向运动，由式(7)可得O点的散射信号为

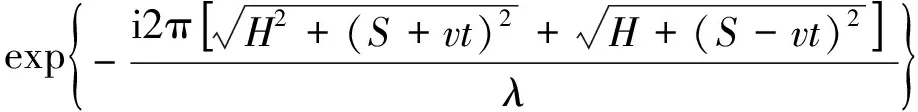
(13)

式(13)中的相位变化项对时间t求导,可得多普勒频移fd为

(14)

图2为根据式(14)得到的不同深度下fd随扫查距离变化的关系曲线，2S为40 mm，v为1 m·s-1，可以看出,衍射回波的调频斜率随缺陷深度变化较大，深度较浅时调频斜率呈曲线变化，深度接近于探头间距的一半时调频斜率趋于恒定，具有线性调频信号的形式。

图2 TOFD法平行扫查时多普勒频移fd随扫查距离变化的关系曲线

考虑到TOFD法在平行扫查时，探头一般不越过焊缝，扫查速度v相对较小，当vt≪S时，即用来进行合成孔径处理的数据窗口在距离远小于探头中心距离的一半时，根据泰勒近似有

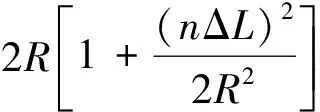
(15)

式(15)的结果与式(9)的结果相同，可见当满足合成孔径窗口距离远小于探头中心间距的一半时，B扫查图像也可采用与D扫查图像类似的匹配滤波处理方法。

2.3 超声波束旁瓣抑制

根据式(5)对TOFD图像进行合成孔径聚焦时，对孔径中心位置左右两侧的A扫信号进行延时叠加过程中采用的是等权叠加。由于TOFD采用的是大扩散角探头，波束旁瓣相对较强，采用等权重叠加会降低对旁瓣的抑制，影响合成孔径聚焦图像的品质。考虑到不同位置数据点对缺陷散射波贡献率的差异，可以对合成孔径窗口不同位置的数据进行幅度加权叠加，孔径中心点分配权重最高，中心点两侧权重依次降低，这样就有效抑制了参与时移运算的波束旁瓣，这种方法称为波束幅度变迹。

结合式(5)可知，需要进行幅度变迹处理的A扫信号数为2N+1，变迹窗函数w(n)需满足在n=0时取最大值1，n=±N时取最小值，在保留最大信息的同时尽可能地消减旁瓣波束，符合上述要求的窗函数有Hanning函数和高斯函数等[17]。经窗函数进行幅度变迹处理的合成孔径聚焦的时移运算可写作

(16)

2.4 TOFD图像的维纳滤波

SAFT能大大提高超声波图像的分辨率，但当原始图像存在较多噪声时，会掩盖图像细节部分，克服这一缺点的方法之一是使用维纳滤波与一系列角度相关参考信号相结合的SAFT[16]。维纳滤波是一种最优线性滤波法，可以对随机信号作平滑滤波和预测，在频域范围内可表示为

(17)

式中：P为滤波去噪后的信号；G为含有噪声的原始信号；H为维纳滤波函数，可由最小均方误差原理求得；H*表示H的复共轭函数；k为大小可调的常数，表示原始图像的信噪比;ω1,ω2为图像频域的两个分量。

在实际的图像中，一般很难准确得到图像信噪比的先验知识，如果把图像划分成M个小块，在小的局部图像空间中信号可认为是稳定的，对于均值为零的白化随机噪声V，其功率谱可与方差相等。维纳滤波器依次作用在小块局部图像空间，滤波函数P(n1,n2)就可以由局部图像信息确定，在时域范围内可表示为

(18)

根据以上所述的SAFT及信号处理算法，采用Labview和C++混合编程的方法，编写了TOFD图像处理软件，其核心算法流程如图3所示。

图3 TOFD图像处理软件核心算法流程

图4 平底孔试块外观及其非平行扫查TOFD图像

3 试验结果

图4(a)为厚度为25 mm的钢制试块，其中心有一个φ5.6 mm的平底孔，距离开口表面的深度为10 mm，图4(b)为其TOFD非平行扫查(D扫)图像，扫查面在开口面的相对面，扫查长度为80 mm，其中维纳滤波窗口大小为4×4，TOFD采样频率为100 MHz，探头规格为φ6 mm，探头角度为60°，中心频率为5 MHz，2S为56 mm。从图4(b)可看出，平底孔上端的TOFD图像呈双圆弧状，靠近直通波的弧线比较明显，为平底孔的主散射图像，下部较短的弧线由部分声波沿平底孔边缘散射引起，其位置在主信号之后，且强度较弱。由于TOFD探头的扩散角较大，旁瓣效应明显，平底孔端部两侧的衍射弧相互叠加，因此缺陷的横向分辨率降低。

图5 经过软件处理后的平底孔TOFD图像

图5(a)为经过维纳滤波后的平底孔图像，背景噪声基本被去除，图5(b)和5(c)为经SAFT处理后的图像，其中图5(b)为海宁窗变迹处理的图像，图5(c)为高斯窗变迹处理图像，图中的虚线为游标线，图底为长度标尺，可看出经SAFT处理后，原有的衍射弧分解重构为三段离散条纹，中间的水平条纹清晰地指示出了平底孔的位置和长度，经测量分别为4.1，4.7 mm，与处理前相比缺陷的横向分辨率提高了。对比图5(b)和图5(c)还发现:海宁窗变迹对衍射波的抑制程度要优于高斯窗变迹对衍射波的抑制程度，而且高斯窗变迹处理后的图像存在一定的偏移，比如图5(a)中缺陷图像的中心位置约为40. 5 mm，图5(b)中缺陷图像的中心位置约为40.6 mm，而图5(c)中缺陷图像的中心位置约为42.1 mm，图5(c)中的结果明显大于图5(a)和图5(b)中的结果。

图6(a)为厚度为20 mm的焊接试板外观，图6(b)为其D扫图像，包括直通波、底波以及二者之间的缺陷衍射图像，扫查长度为250 mm，探头中心间距为38 mm，整个图谱经过4×4窗口大小的维纳滤波处理。对图中红色方框内的TOFD图谱进行SAFT处理，孔径数为27，处理后的结果如图6(c)所示。对比发现，经SAFT处理后抑制了缺陷处的弧状衍射波，提高了缺陷的横向分辨率。

图6 焊接试板外观及其D扫TOFD图像

4 结论

从SAFT的基本原理出发建立了D扫和B扫TOFD图像的合成孔径聚焦成像模型，研究了匹配滤波和维纳滤波等方法在TOFD图像上的实现途径。对TOFD图像信号处理算法进行了优化设计，实现了TOFD图像的合成孔径聚焦技术与匹配滤波、维纳滤波、旁瓣抑制等算法的综合集成，并通过自编软件进行了试验验证。结果表明，提出的合成孔径聚焦图像重建算法成功实现了对TOFD图像的重建，有效提高了缺陷的横向分辨率，有助于TOFD技术的实现。