基于波原子稀疏优化与组稀疏表示的压缩感知算法

胡春海，马双娜，李永发

(燕山大学 电气工程学院，河北 秦皇岛 066004)

0 引言

随着信息技术迅猛发展，人们对信息的需求日益剧增，从模拟到数字信号的转换一直严格遵守采样率必须达到超过信号频率2倍的奈奎斯特采样定理才能满足信号的准确重建。传感系统为获得更精准的信号，需要处理的数据量大大增加，对其信号处理的能力提出了更高要求，也给相应硬件设备带来极大的挑战。为解决以上问题，学者们提出了一种压缩感知[1-2]理论。压缩感知指出信号可以通过远低于奈奎斯特定理的采样频率来恢复和重建。它能够大大降低信号采样频率、信号处理时间以及计算、储存和传输数据的成本。压缩感知通过对信号的采样实现数据压缩，压缩后的信号更有利于传输和储存，压缩信号通过特定的压缩感知重构算法进行信号重建，只需要对数据进行测量就可以对原始信号实现高压缩比、高效率的数据处理。2014年Zhang提出组稀疏表示(Group-based Sparse Representation，GSR)[3]的图像压缩感知算法。根据自然图像的非局部相似性，将图像分块并寻找每个相似块组的稀疏表示进行压缩感知。传统的组稀疏重构算法缺乏对图像整体稀疏性的研究，本文提出一种约束矩阵对图像的波原子变换系数进行约束实现图像稀疏化预处理，并采用组稀疏表示的图像重构算法进行实现图的压缩感知重建。

1 压缩感知理论

压缩感知理论主要包括三个方面：信号的稀疏表示、测量矩阵的设计和重建算法[4]。信号可以进行压缩感知的必要条件为信号能够在某特定的变换域中稀疏表示[5]或自身稀疏。压缩感知利用测量矩阵[6]对信号进行测量获得测量值，测量矩阵要求符合约束等距性条件(Restricted Isometry Property,RIP)[7]，最后通过压缩感知的重构算法完成信号重建。

1.1 稀疏表示

信号本身一般不是稀疏的，但是能够通过某种变换使其稀疏。文献[1]中Donoho指出：如果信号x∈RN×1，在变换域Φ中有L个非零系数，且信号x在变换域Φ中是L-稀疏的，则稀疏表示能够使信号通过在变换域中用有限的基函数表示。正交变换基Ψ下信号x的稀疏表示为

x=Ψ·s，

(1)

s是稀疏向量，采用测量矩阵Φ(大小为M×N)对x进行采样，则有

y=Φ·Ψ·x。

(2)

得到测量值y中包含重构x所需的信息，其中Φ与Ψ不相干。常用的稀疏表示方法有离散余弦变换、傅里叶变换和小波变换[8-9]等。

1.2 测量矩阵

若满足信号重建要求，稀疏变换矩阵Ψ和测量矩阵Φ则需要具有不相干性，且测量矩阵Φ要求满足RIP特性。对任意的l=1，2，…，L，定义矩阵Φ的等距常量δl为满足下式的最小值：

(3)

式中，x为L项稀疏向量，0<δl<1，称矩阵Φ满足l阶RIP。

压缩感知中用作测量矩阵的有随机高斯矩阵、哈达玛矩阵、伯努利矩阵和Toplitz矩阵[10]。等。随机测量矩阵的列数远远大于行数M≪N,当测量数M≥clog(N/K)时,便会以极大的概率满足RIP条件，且随机高斯矩阵Φ与大多数变换基矩阵Ψ高度不相关。Candes等[11]证明在压缩感知中高斯随机测量矩阵能够以很大概率满足RIP特性，可以作为普适的测量矩阵。

1.3 重构算法

测量值y经过储存传送等过程，最后需要在终端进行重构。由y重构信号x的方程属于欠定问题，未知数远远大于方程数量导致方程存在无数解。故可以将问题转换为由y恢复s，因为s是k稀疏的且未知数远小于x。稀疏过程为

y=Φx=Φ·Ψ·s。

(4)

根据以上条件可以从y中采取非线性优化的方法来恢复信号x。压缩感知信号重构问题最直接有效的方法是利用最优l0范数式的方法来重构稀疏信号s，即

xopt=Ψsopt，

(5)

sopt=arg min‖s‖0s.t.ΦΨs=y。

(6)

这是压缩感知的核心思想，压缩感知由少量线性测量通过求解最优化问题(5)直接得到信号x的压缩表示，使得超高分辨率信号获取成为可能。在此利用最优l0范数重构信号方法的基础上又提出了范数类、匹配追踪类等各类压缩感知算法[12]。

2 组稀疏表示压缩感知算法

图1 图像块与图像块组
Fig.1 Image block and image block group

(7)

引入平衡参数λ将式(7)转换为无约束问题：

(8)

采用迭代收缩阈值算法求解，利用式(9)重构图像：

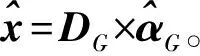
(9)

3 波原子变换稀疏优化

3.1 波原子变换

由于小波基无法较好地去逼近奇异性曲线，二维图像通过小波变换进行表示时造成图像几何特征会包含不同的小波系数子带，导致图像的小波变换并不能很好的用于稀疏表示。2007年Demanet等人提出了波原子变换[15]，波原子振荡周期和支撑域尺寸满足关系：wavelength≈(diameter)2。波原子可以看作方向小波与Garbo原子的“插值”形式，相对与Bendelet、Contourlet和曲波等对图像的纹理细节信息有更好的稀疏表示[16]。

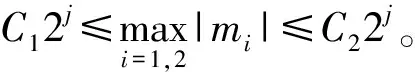
在二维波原子变换中：

(10)

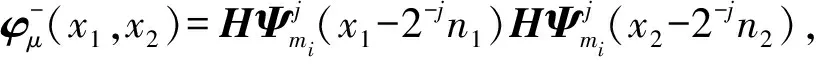
(11)

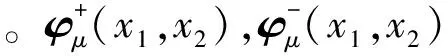
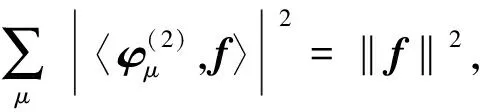
(12)

二维波原子变换系数：

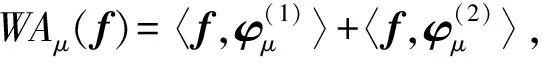
(13)

在j=3，m=(3,2)的尺度下二维波原子基函数的空域和频域图形如图2所示。

图2 二维波原子基函数图形
Fig.2 2-D wave atoms basic function graph

波原子具有最优表示图像方法的特征，能够很好的非线性逼近奇异值曲线，对纹理细节信息表征优于曲线波。图3(a)为大小为256×256的指纹图像,(b)、(c)为分别经小波变换和波原子变换后以最大的512个系数的重构图像。

图3 图像小波变换与波原子变换重构结果
Fig.3 Image wavelet transform with wave atoms transform reconstruction results

3.2 优化矩阵设计

波原子变换可以使数据变得稀疏，但稀疏后数据压缩感知重建效果仍不太理想。根据变换域系数数据显示逐渐递减的趋势，所以对波原子变换较小系数进行抑制[17]。因此针对变换系数特点设计了系数约束矩阵：

(14)

系数约束矩阵为n维的对角矩阵，m为所在行数。其中变量j满足

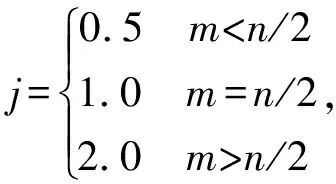
(15)

图像经过波原子变换得到图像波原子变换系数，波原子变换系数乘以约束矩阵得到优化后波原子变换系数。图4为图像barbara.bmp的波原子变换系数，图5～6为系数抑制与逆抑制结果，从图4～6对比可以看出优化后波原子变换系数中较小系数被抑制，变换系数稀疏度大大改善，此优化稀疏过程可逆。

图7为图像barbara.bmp与图像经过波原子稀疏优化后结果，波原子稀疏优化增强图像稀疏性。

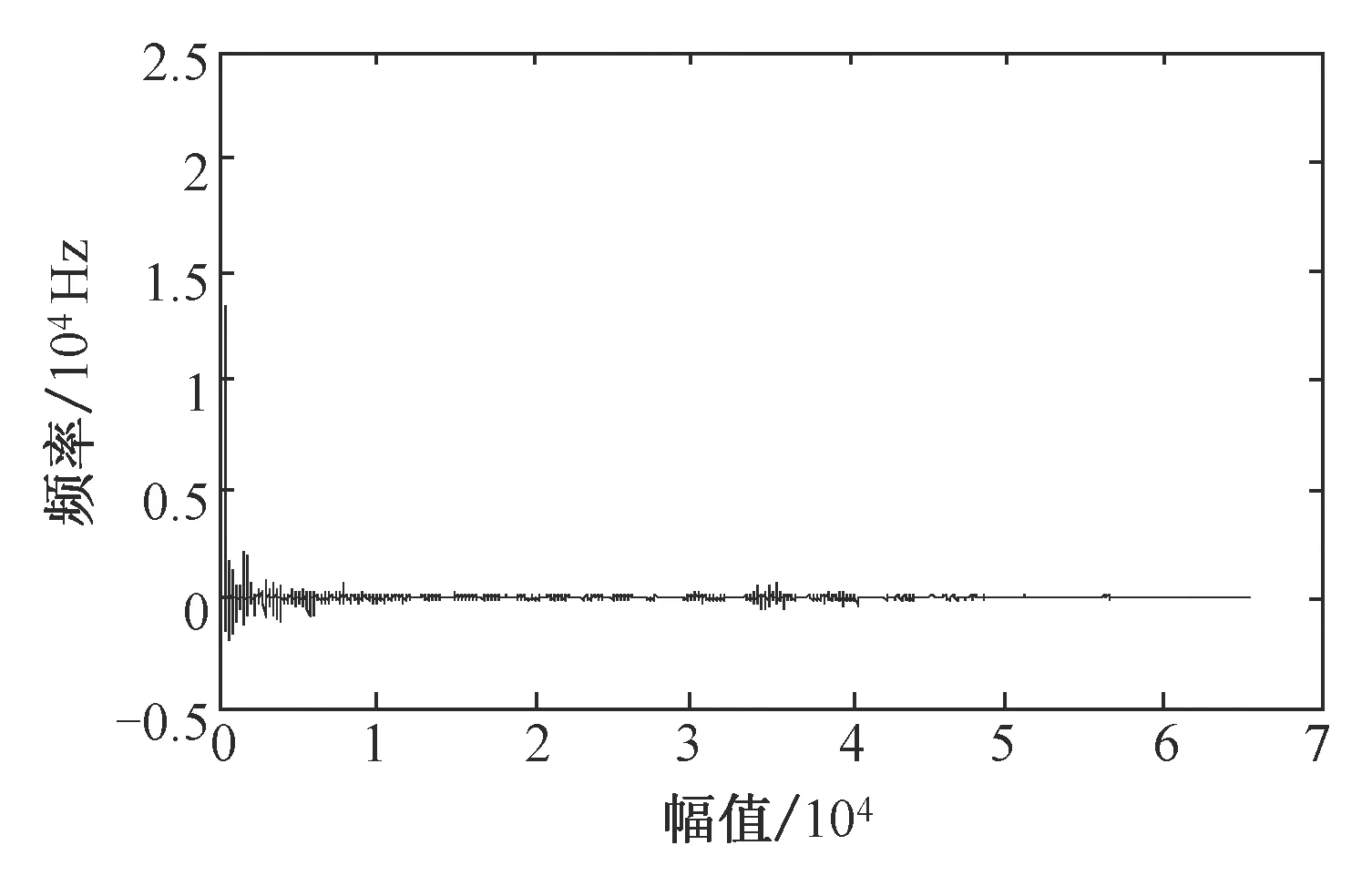
图4 图像波原子变换系数
Fig.4 Image wave atoms coefficients

图5 波原子系数抑制结果
Fig.5 Wave atoms coefficients suppression result

图6 波原子系数逆抑制结果
Fig.6 Wave atoms coefficients inverse suppression result

图7 原图像与波原子稀疏优化结果
Fig.7 The original image with wave atoms transform sparse optimization results

4 仿真实验

仿真实验硬件环境为Intel Pentium E5405,CPU 2.5G主频，4G内存的计算机，软件环境为Win10 64位操作系统，MATLAB R2012a。本文采用大小为256×256的barbara等国际标准灰度图像进行压缩感知重建的仿真实验。为了消除实验随机性，实验结果取在相同的采样率下200次的平均值，实验以峰值信噪比(Peak Signal to Noise Ratio，PSNR)作为图像质量评价指标。

算法具体实现步骤：

1) 构建抑制矩阵对原始图像进行波原子变换系数稀疏优化并重建；

2) 对图像按像素大小为32×32分块并重组，采用高斯测量矩阵压缩采样；

3) 自适应字典学习获取字典DGk；

4) 通过本文算法重构原图像；

5) 对重构图像进行波原子系数逆抑制，恢复原图像。

表1为barbara等4幅图像在采样率为0.1、0.2和0.3下GSR算法和本文方法实现图像压缩感知重构实验结果，从实验得到的重构图像PSNR相比较可以看出，本文方法在采用不同图像和不同采样率情况下重构图像质量均明显高于GSR算法。由于图像本身复杂程度和稀疏程度不同，重构图像质量有所差异。

表1 图像压缩感知重构PSNR

Tab.1 Image comprised sensing reconstruction PSNR dB

图8为采样率为0.08的实验结果，从以上4组实验重构图像结果可以看出GSR算法在较低采样率下无法准确恢复图像边缘纹理等信息，本文算法相较于GSR算法能更有效地恢复原图像的细节边缘部位，重构图像质量更清晰。

图8 图像压缩感知重构结果
Fig.8 Image compressed sensing reconstruction results

图9为图像barbara由GSR算法和本文方法在采样率0.05到0.5下的重构质量对比结果。从图9中可以看出本文算法相较于原有的GSR算法在不同的采样率下的PSNR均有所提高，尤其在低采样率下效果明显高于GSR算法。

图9 图像重构质量对比
Fig.9 Image reconstruction quality

从图8和图9实验结果可以看出本文算法对于不同的图像在各个采样率下的重建效果相较于原有的算法重构质量更好,在相同采样率下峰值信噪比更高，能够更好地恢复图像纹理细节信息，峰值信噪比更高。

5 结论

本文提出一种基于波原子系数稀疏优化的组稀疏表示图像压缩感知算法，通过构建一种约束矩阵对图像波原子变换系数进行约束使得图像变得更加稀疏。图像的整体稀疏性增强能够有效地提高图像压缩感知重构算法图像重构质量，仿真实验表明在相同采样率下本文算法较GSR算法具有更高的峰值信噪比，使得图像的重建效果更好，尤其是在低采样率下表现出的对图像边缘细节恢复能力更高，从而使得本文方法能以更低采样率实现满足需求的图像压缩。