基于ID预测模型的明渠系统控制参数在线优化研究

苏海旺，管光华，钟 乐，陈 琛，叶雯雯

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 中国电建华东勘测设计研究院有限公司，杭州 310014)

0 引 言

输调水工程的修建是解决我国水资源分配不均、水污染严重、水生态恶化等问题的措施之一。长距离输水工程采用自动化运行控制技术，可大大提高渠系的运行调度水平，改善输水效率，降低运行管理费用等。自上世纪末至今我国在相关方面的研究已取得了一定成果，但现有控制算法依然存在一定弊端[1]，如为使控制模型更加精确，会导致算法复杂，计算量大，同时鲁棒性差；渠池之间耦合关系不易解决和常规PID控制算法应对突变敏感性较高等问题。预测控制作为一种新型的计算机控制算法[2]，基于离散控制系统，通过滚动优化和反馈校正弥补了控制系统精度上的不足，抑制了扰动，提高了系统的鲁棒性，在处理非线性系统优化问题时有极大优势[3][4]。在此背景下，研究人员将模型预测控制(MPC)[5,6]改进后应用于渠系自动化控制过程。王长德等人[7]将预测控制中的动态矩阵控制(DMC)引入渠系自动控制，并设计DMC控制器[8]，通过对单渠段系统建立动态矩阵控制模型，分析其稳定性。Wahlin[9]将模型预测控制的USWCL应用于渠道运行控制，通过直接作用于渠道的控制机构实时监测渠道里的水深、流量和闸门开度的变化，以实时的模型辨识来完成对渠道自动化的控制。对于渠道控制模型ID模型[10]，国内学者(如穆祥鹏[11]等)通过初步研究证明其可对渠道进行描述。

本文在前人的研究基础上，基于下游常水位运行方式[12]，提出建立ID预测模型，运用ID模型对渠道运行过程进行实时预测，实现PID参数在线优化，以改进传统PID控制算法[13]，通过不断优化选择PID控制器反馈控制参数，以达到其最优输出，降低渠池中水深的超调，减少渠道水深波动时间，使下游水深更快地稳定在目标水深。

1 渠系运行控制系统模型

渠系控制系统主要由控制模块、流量计算模块及水位计算模块组成(如图1)。控制模块为整个控制系统的核心部分，以水位的偏差和偏差变化率作为输入，以闸门的开度增量作为输出[14]。

图1 渠系控制系统流程图Fig.1 Flow chart of canal control system

本文中过闸流量公式采用美国中亚利桑那调水工程(CAP)运行控制模型的弧形闸门过闸流量计算公式[15]：

(1)

式中：Cd为流量系数；a为闸门开度，m；b为闸门宽度，m；yu、yd分别为闸门上、下游水深，m；Q为过闸流量，m3/s；Au为闸门上游过水断面面积，m2。该式在弧形闸门自由出流和淹没出流的情况下均适用，流量系数Cd根据水流状态选取不同值。

2 模型预测控制

2.1 PID控制器

PID控制器是经典控制理论中最具代表性的控制器，具有原理简单，易于实现和适应面广等优点，长期以来被广泛应用，离散化的PID方程[16,17]为：

(2)

式中：k为采样序号，k=0,1,2,…；u(k)为第k次采样时刻的控制器输出，即闸门的开度增量；e(k)为第k次采样时刻输入的偏差值，即第k次采样时刻的水位差；e(k-1)为第(k-1)次采样时刻输入的偏差值；KP为比例系数；KI为积分系数；KD为微分系数。

在PID控制器中，比例环节用于减小水位偏差，使过程较快达到稳定；积分环节用于减小闸门处水位控制的稳态误差，提高系统控制的精确性，消除系统残差；微分环节主要反映水位偏差的变化趋势，并在其偏差急剧变化前引入一个早期的修正量，从而加快闸门的控制动作、减小调节时间。

2.2 ID模型

ID模型由Schuurmans[18]在1995年提出，可同时处理正常水深段和回水区域，与其他模型相比更接近工程使用。

该模型以一个渠段为计算单元，进行分区建模，将渠段划分为回水区域和均匀流部分，用积分环节(I-Intergrator)模拟回水区域和用滞后(D-Delay)环节模拟均匀流区域，其表达式写作：

(3)

式中：e为下游水位偏差(相对稳态水位)，m；qin、qout分别表示渠池上游入流和下游出流流量的变化量，m3/s；t为时间，s；τ为滞后时间，即上游变化通过均匀流段传到下游回水区所需的时间，s；As为渠池回水区域面积，m2。

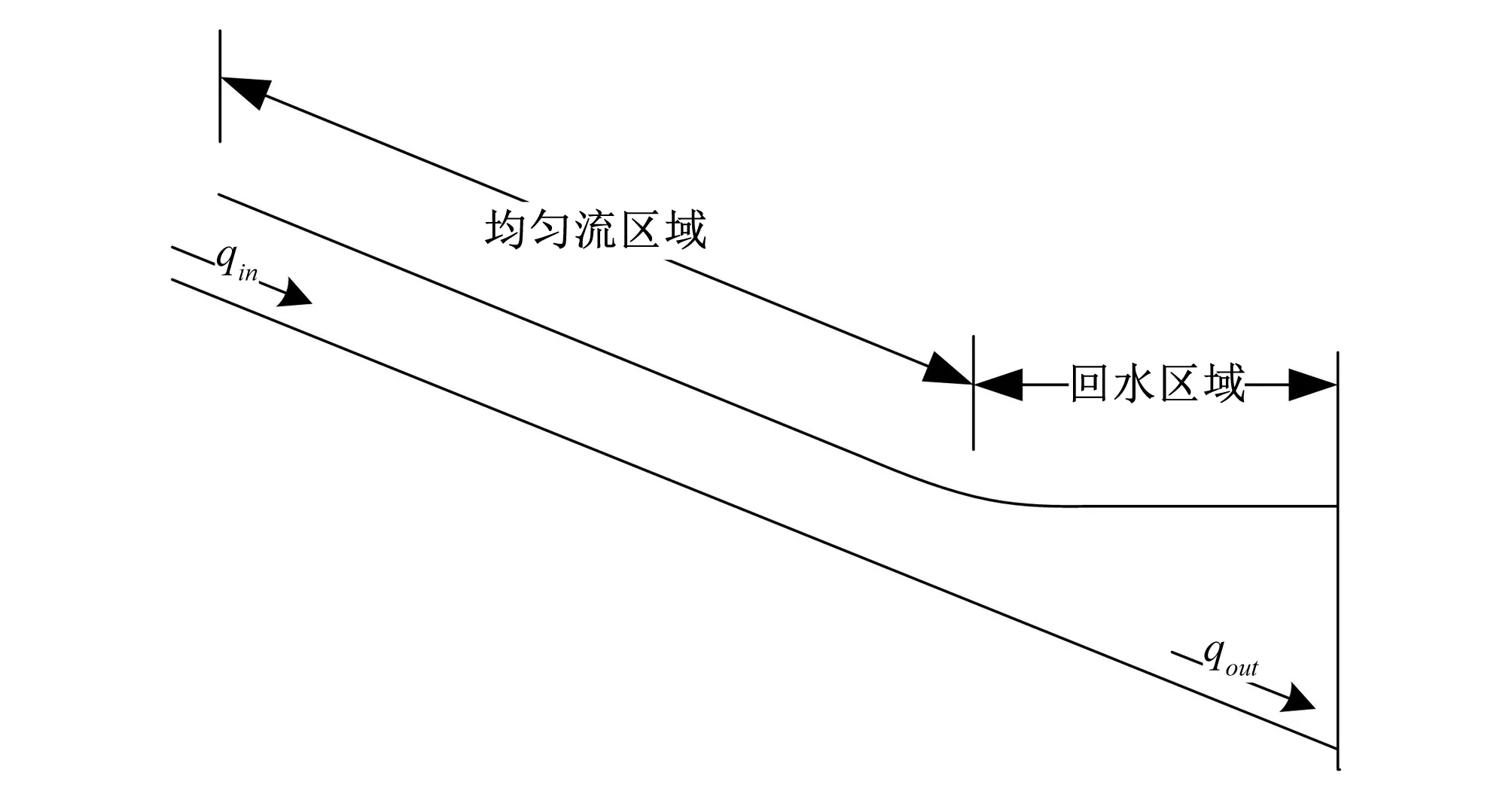
图2 ID模型简化示意图Fig.2 The schematic diagram of ID model

2.3 基于ID模型的预测控制

图3为基于ID模型预测控制优化PID的框图，其包含预测模型、滚动优化和反馈校正三个部分。控制系统控制器为传统PID控制器，模型预测控制通过预测并调整PID控制器的参数，间接控制渠道闸门的开闭过程，完成对渠系流量过程的控制。

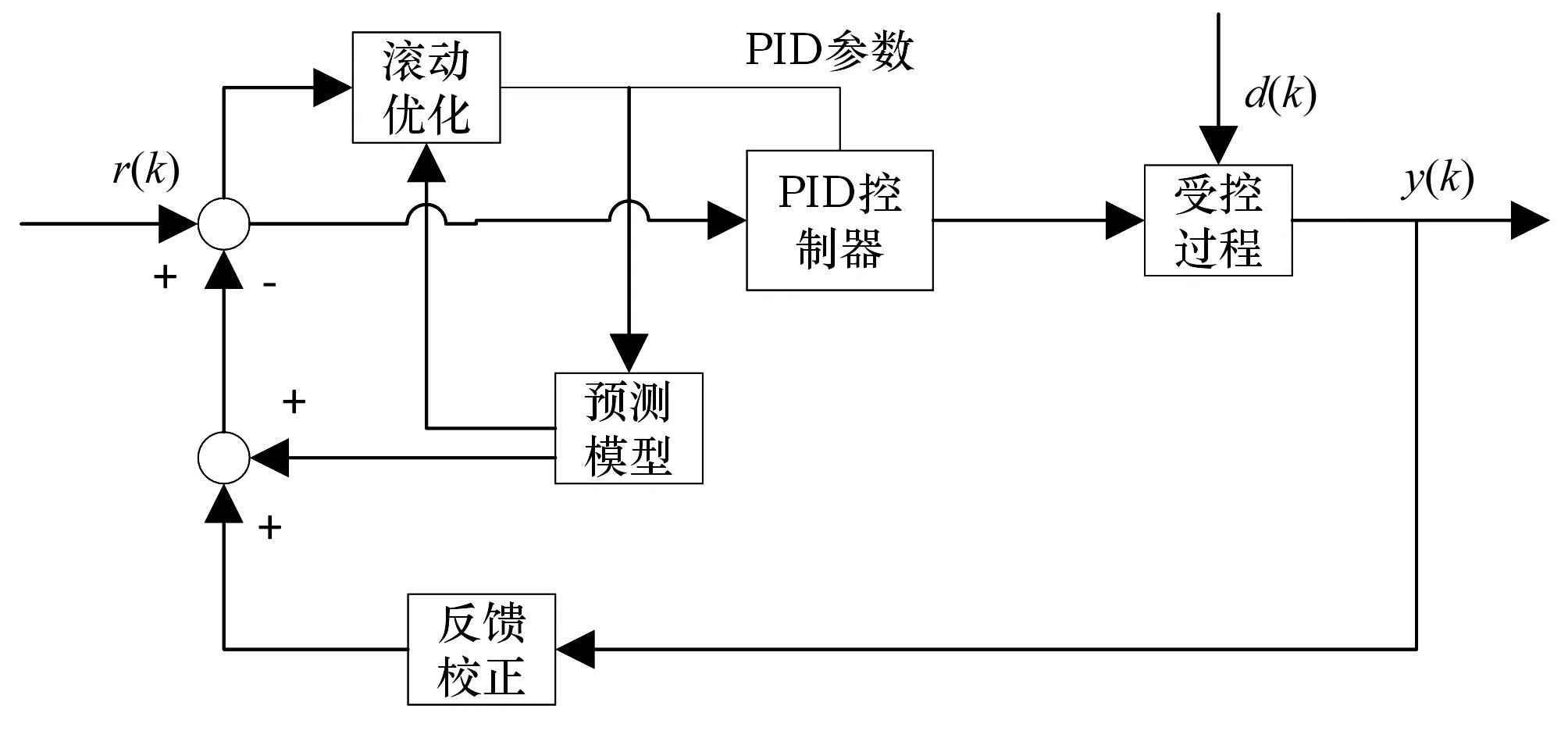
图3 模型预测控制优化PID框图Fig.3 Model predictive control optimization of PID diagram

2.3.1 预测实现

预测模型的功能是根据被控对象的历史输入输出信息和未来可能的输入信息，预测未来输出。在渠系建模时，选取水位作为输出[7]，用y表示，以闸门开度和流量为输入，分别用u和q表示。

首先测定阶跃响应的采样值αi=a(iT),i=1,2,3,…，N。T为采样的周期，在第NT时刻之后目标水位基本达到稳定。当K时刻闸门开度有一增量Δu(k)时，根据过闸流量公式(1)，可得qin。假设单渠池中qout为0，即下游出流流量保持不变，可由ID模型式(3)求得水位变化值e(k)，即可求出未来时刻目标水位的预测值：

(4)

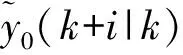
2.3.2 滚动优化

选取能同时体现系统控制作用和控制器性能的参数作为优化指标，以此来确定最优的控制作用。优化性能指标只作用于从该时刻起到未来有限时段，而当到达下一采样时刻之后，这一优化时段向前推移。

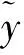
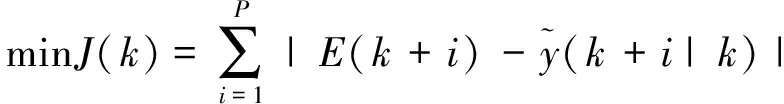
(5)

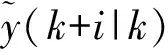
2.3.3 反馈校正

为防止外界环境或模型失配造成的预测误差，预测控制通常只实现本时刻的控制作用，到下一采样时刻时，须将实际输出与预测输出进行对比，并反馈到控制系统中进行校正，再进行新的优化。

误差信息反映了模型中未包括的不确定因素对下游水位的影响，可对模型进行在线修正：

(6)

式中：yerr(k)为预测误差；α为反馈校正补偿系数，其取值范围为[0,1]。

综上，通过反馈校正不断在线进行，将前一时刻的预测误差用作这一时刻的修正量，保证系统预测的精确性。

3 仿真实验分析

选取漳河灌区三干渠三分干分水闸到卞庙节制闸渠段的单个渠池进行仿真建模，验证预测模型并测试其预测效果。仿真渠池参数见表1。

表1 仿真渠池参数表Tab.1 Properties for simulation pool

使用武汉大学开发的输水渠道系统运行仿真与控制软件V1.0中的程序包[19]进行仿真计算，对比分析由仿真模型与预测模型计算所得的下游闸前水位。

3.1 预测模型验证

设置一斜坡流量工况条件，分水口入渠流量在第6 h开始到第12 h，由0 m3/s加大到6 m3/s，仿真总时长48 h。

设置两组PID控制器参数：①KP=1.0，KI=0.2，KD=0.2；②KP=2.0，KI=0.2，KD=0.2，使用仿真平台进行仿真，对比传统PID控制与预测控制模型仿真结果，结果如图4所示。

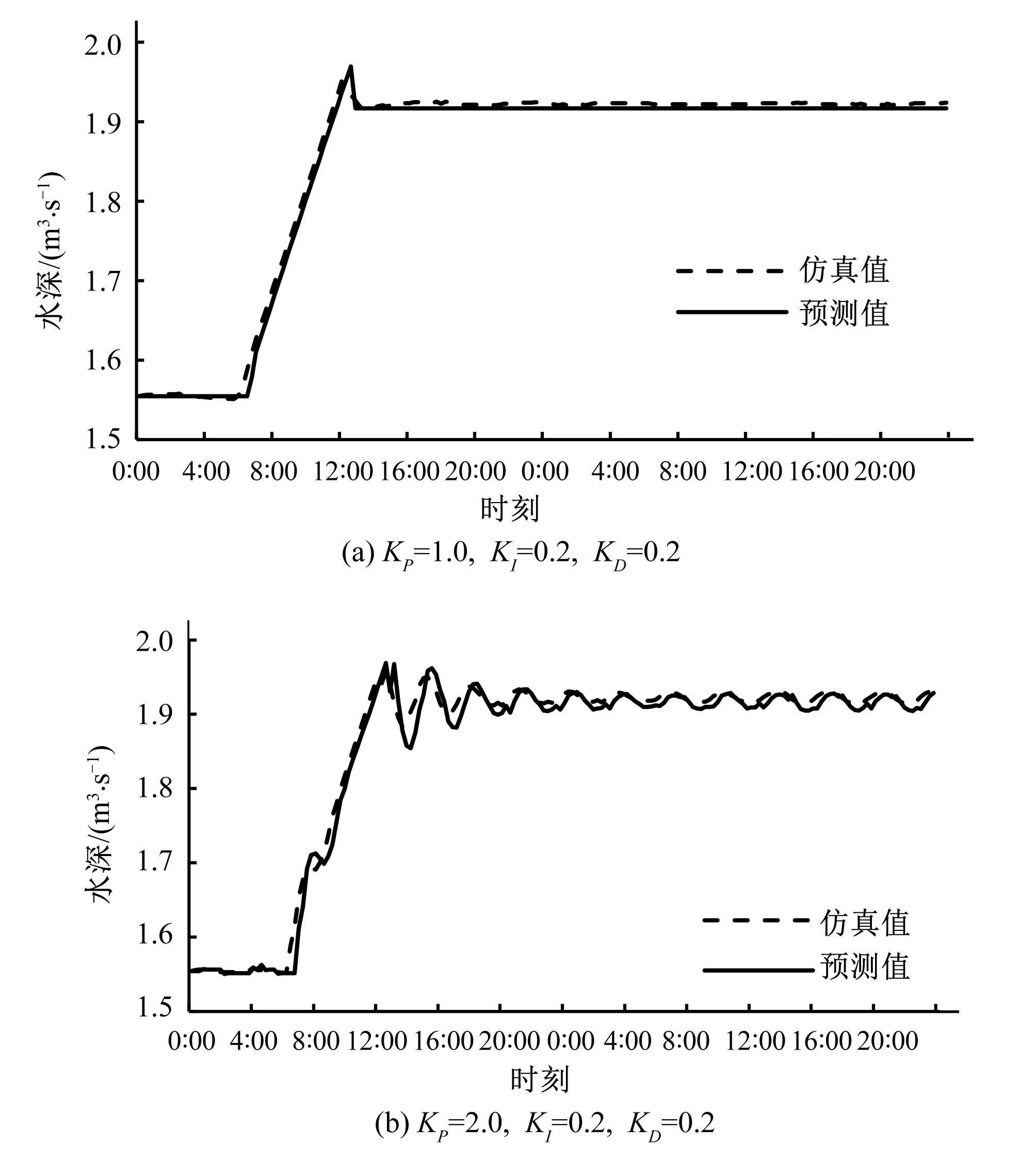
图4 仿真值和预测值对比Fig.4 The simulation and predicted value

由图4可知，两组预测数据整体均符合仿真结果的变化趋势，说明在流量变化引起水位波动的工况下，用预测模型对下游闸前水深进行预测的结果有较高的精度，可为控制参数的选择提供依据。

3.2 预测效果评价

设置一阶跃流量工况条件，取渠池初始入流量为4 m3/s，第6 h时增加到6 m3/s，仿真总时长为48 h。

3.2.1 离线初值设定[20]

本文选取对控制调节起主要影响的KP作为调节值。经过多次调试发现，当KP值达到2.5时，仿真的流量过程会失稳。为保证仿真过程稳定，将KP的取值范围设置为[0,2.5]，步长为0.5，给出5组PID控制参数的预设值，见表2。

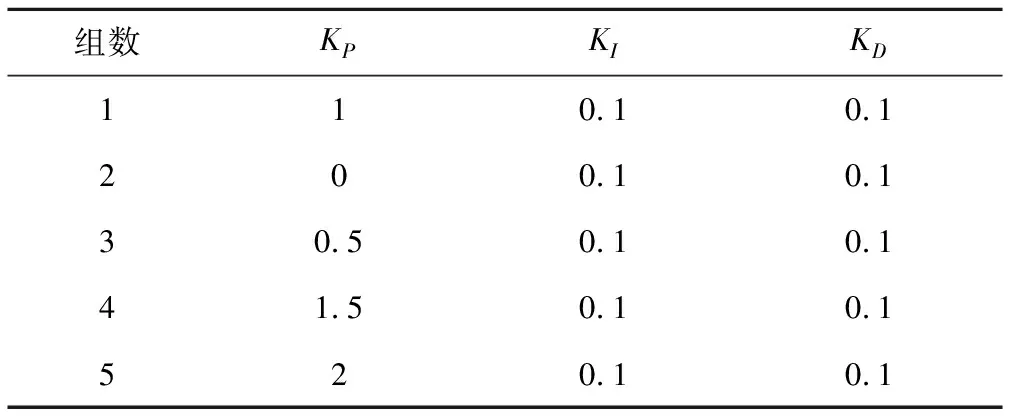
表2 PID参数预设值Tab.2 Preset values for PID

3.2.2 预测时域选择

预测时域即模型可以预测的时间范围。预测时间范围越长，模型预测控制的效果越好，但计算量会越大，计算时间越久。合理的预测时域，不仅可以节省计算时间，减少计算量，又能满足预测控制的精度要求。

本文选取1、2、5、7个步长的预测时域，针对上文所述的阶跃流量工况进行模型预测控制仿真计算，结果如图4所示。由图可知，在该仿真工况下，仿真结果和预测时域的选择关联性不高，考虑到单渠池中ID模型的计算速度很快，本文在仿真实验中选取预测时域为7个步长。

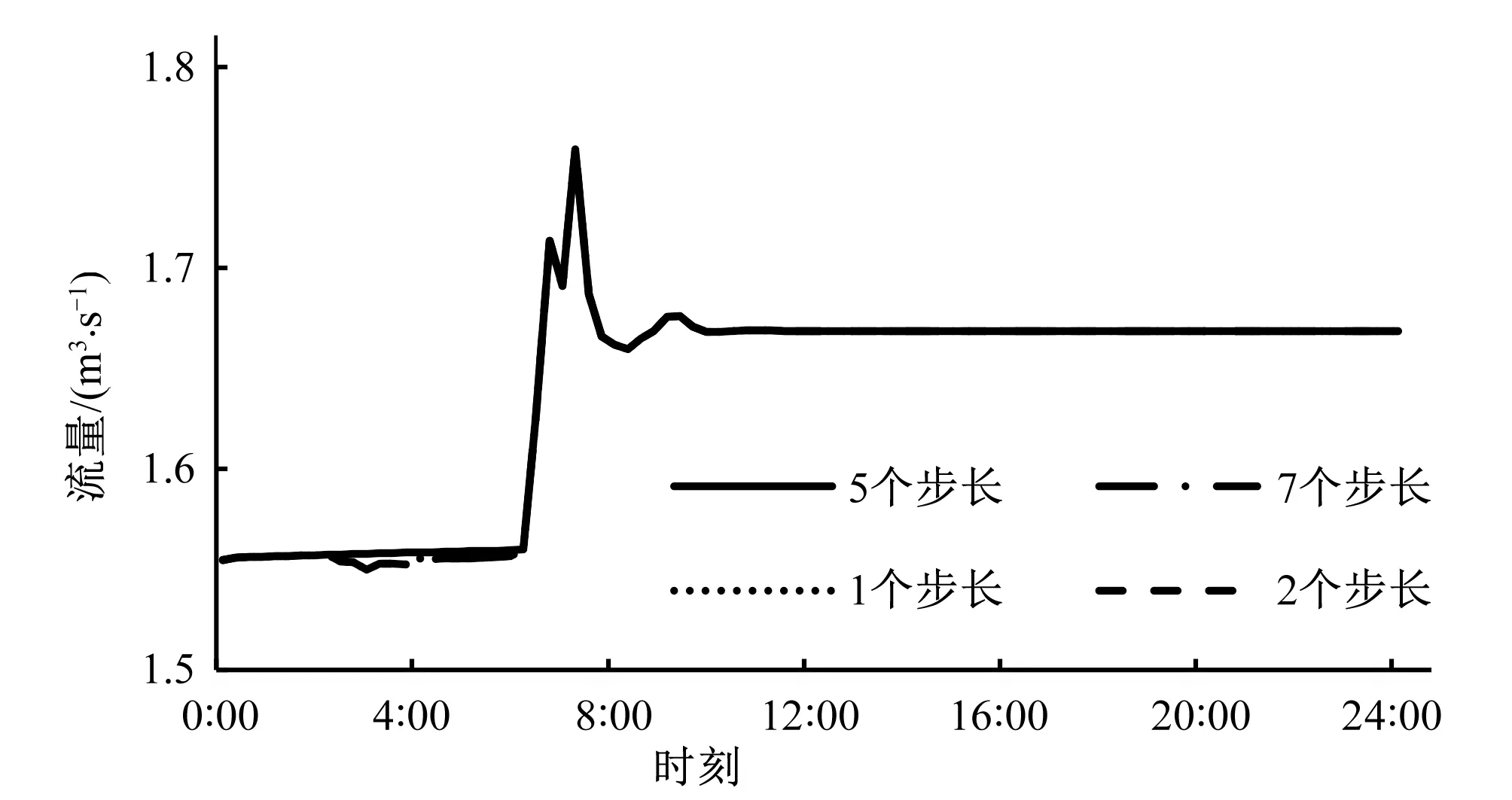
图5 不同预测时域仿真图Fig.5 The simulation diagram of different prediction time domain

3.2.3 仿真结果分析

根据输水渠道系统仿真程序计算出K时刻下游水位变化和进出口流量变化后，利用模型预测控制预测5组不同PID控制器在K+7时刻的水位变化值，并选取预测值与目标水位最为接近的PID控制器作为K+1时刻输水渠道系统仿真程序的控制器，如此往复循环，通过模型预测控制逐步优化PID控制器的参数，间接使PID控制器控制性能达到最优。仿真结果如图6所示。

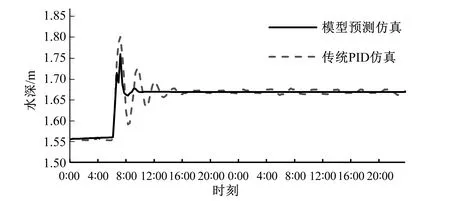
图6 模型预测和传统PID仿真对比结果Fig.6 Results for model prediction and traditional PID simulation

由图6可知，加入模型预测控制的PID控制器，水位超调得到了有效降低，系统稳定时间缩短。其中传统PID控制器的最大超调量为0.25 m；模型预测控制作用下的PID控制器最大超调量为0.21 m，减小了16%；传统PID控制器作用下，下游水深在18 h左右开始趋于平稳，并出现周期性波动，加入模型预测控制后在第10 h左右达到稳定。

在仿真结果的基础上，采用稳定时间、最大超调、IAE(%)和IAQ(m3/s)4个控制器性能指标对模型预测和传统PID控制器的控制效果进行对比。其中IAE和IAQ指标计算公式为：

(7)

(8)

式中：Δt为采样时间步长；t1、t2分别为流量开始变化和稳定时刻；Qt为t时刻过闸流量。

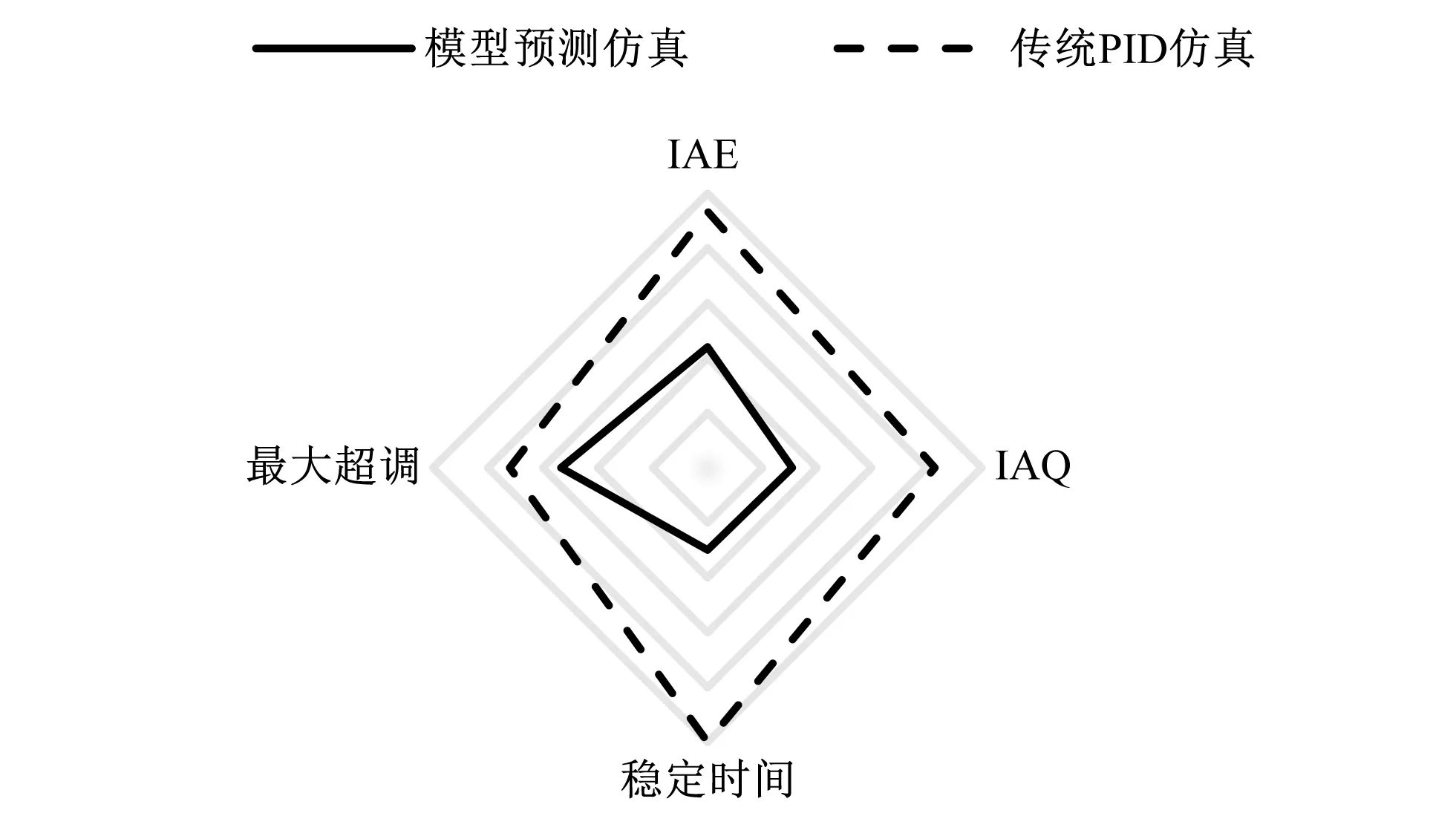
图7 控制器性能指标对比图7 Performance comparison of the controller

从图7可以看出，模型预测控制4个性能指标值均小于传统PID控制，表明模型预测控制在传统PID算法的基础上系统超调减小、闸门调节量减少，同时响应速度提高。由此可知，模型预测控制优化的PID控制器优于传统PID控制器。

3.3 结 论

本文在传统PID控制器的基础上，加入ID预测模型，通过在线不断滚动优化和反馈校正的方法获取当前时刻最优PID控制器参数，有效减小了水位超调，缩短了稳定时间，提高了响应速度和系统的控制性能，验证了模型预测控制应用于明渠的优越性。本文得出以下结论：

(1)文中使用的预测模型ID模型用于渠道水位的预测具有较高的精度，同时该算法计算简单、速度快。

(2)通过引入模型预测控制，不断在线调节PID控制器参数来优化PID控制器，避免了传统PID控制器全程使用一套控制参数的弊端，使PID控制器的性能达到最优。

(3)在预测时域的选择上，本文分别选择预测时域1个步长，2个步长，5个步长和7个步长进行模型预测控制，发现预测结果和预测时域的选择关联性不高。

4 结 语

本文提出将ID模型用于预测控制，并对其在渠道控制过程中的作用效果加以验证，初步证明ID模型在单渠段的运行控制中对缩短稳定时长、提高控制精度有显著效果。在下一步工作中，计划将基于ID模型的模型预测控制器应用于串联多渠池中，在需要考虑上下游流量和水位耦合的情况下，对模型预测控制的效果作进一步的研究。

□