基于改进距离和的异常点检测算法研究

李春生，于 澍，刘小刚

(东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318)

0 引 言

随着网络和信息技术的广泛普及，人们在日常活动中会产生大量的数据，而从这些数据中发现某种未知的规律，挖掘其中隐含的信息与知识，成为了研究者们的研究乐趣。在这个过程中，数据预处理占据了较大的一部分，其中很重要的一方面就是对于异常数据的识别，即异常点检测技术，它会影响后续数据挖掘模型的预测效果和实用性。异常点又叫做噪声、孤立点、离群点等。然而发现的异常数据并不能简单地直接剔除掉，不仅会影响数据的连续性，而在某些领域中，这些被认为是不正常的数据隐藏着更有价值的信息，例如把异常点检测技术应用到以下领域：保险理赔，银行交易中的欺诈检测及风险分析；医药研究中药品所产生的异常反应[1]；网络安全方面入侵行为的检测。

目前，异常数据的挖掘算法大致有基于统计、基于距离、基于密度、基于聚类等。其中传统的基于距离的异常数据挖掘算法原理较为简单，使用方便，在数据集分布均匀的情况下，检测效果较好，但存在以下缺陷：参数设置复杂，检测效果对参数要求较高；异常数据并不是存在于所有属性上，只存在于某些影响数据稳定性的属性上；当数据集分布不均匀时，可能会出现偏差，不能有效地检测出异常点。

为了解决上述问题，提出了一种基于改进距离和的异常数据检测算法；对于终端的不确定性选择属性困难的问题，引入了“属性隶属度”的概念；用改进的距离进行异常点的检测，给出了异常点的异常程度。

1 基于距离的异常点检测

1.1 异常点检测方法

最先提出基于距离的异常点检测方法的是Knorr和Ng[2]，他们认为的异常点是这样的：在数据集中至少有k部分数据点之间的距离大于某一阈值d。其实质是将异常点看作是在d范围内邻居较少的点。基于距离的异常点检测算法一般分为以下三种：

(1)基于索引的算法(index-based)[3]。

该算法首先建立了一个多维索引结构，然后根据该索引结构查找出各个数据点在半径为d的范围内的邻居。需事先设定临界个数k，在查找过程中当某点的邻居个数一旦大于k，则说明该点不是异常点，立即停止查找，并标记该点为正常的数据点。直至将所有点都做好是否为异常点的标记。在最不理想的情况下该算法的复杂度为O(s*n2)，其中s表示数据的维数，n表示数据点的个数。由于构建索引结构需要的时间较长，所以该算法是非常耗时的，因此应用较少。

(2)基于循环嵌套的算法(nested-loop)[4]。

为了避免建立索引结构，提出了一种基于循环嵌套的算法。首先将数据集均匀分成若干数据块，同时将内存缓冲区均分为A和B两部分。然后将未在该区存储过的数据块读入A部分，其他数据块依次由B部分读取(每次只读取一个)。最后计算A和B两部分的数据块中每对数据对象之间的距离，并记录A部分的每个数据对象的邻居数。一旦大于k个，则停止计算，A部分继续读取下一个数据块；若小于k个，则B部分继续读入下一数据块。直至读取完所有的数据块，并累加邻居数。该算法的时间复杂度与第一种算法的复杂度相同。

(3)基于单元的算法(cell-based)。

1.2 距离的度量及异常点的定义

常用的距离度量方法有曼氏距离、欧氏距离、切比雪夫距离等。

对于两个m维空间中的数据点xi与xj，它们之间的欧几里得距离和曼哈顿距离可以由明考斯基距离来概括，即：

(1)

其中，当q=1时为曼哈顿距离，表示为：

(2)

当q=2时，表示为最常用的欧几里得距离：

(3)

其中，xik表示在第k维的第i个分量；xjk表示第k维的第j个分量。

切比雪夫距离表示为各坐标数值差的最大值，即：

(4)

常用距离度量种类比较多，使用哪种距离度量要看算法应用的具体领域。用不同的距离度量进行计算，得到的结果也可能是不同的。

常见的基于距离的异常点定义有以下几种：

(1)在数据集S中，若点O是异常点，那么至少有p部分对象到点O的距离大于d，也就是说，如果点O在以d为半径的范围内，有不超过M个点的邻居，那么点O就是一个带有参数p和d的异常点，表示为DB(p,d)，这里M=n(1-p)，n是数据集S中的数据对象个数。

(2)异常点是指数据集S中的n个点，这n个点到其第k个最近邻点的距离是其他所有点中最大的，其中n是异常点个数的估计值。

(3)在数据集S中，取前n个与其k个最近邻点的距离之和最大的点，则这n个点就是异常点。其中n是异常点个数的估计值。

尽管以上几种定义都各不相同，但都是基于距离的异常点的定义。文中将使用第三种定义来判断数据集中的某个点是否为异常点。

2 基于改进距离和的异常点检测

公式中的参数及其意义如表1所示。

表1 参数及意义

2.1 检测属性的选取

在数据集中，异常点并不是存在于每个属性上，它们只是在其中某一部分属性上出现异常状态。一般情况下，都是由该领域的专家来选取这些有研究价值的属性，但是当终端操作人员不具备相关的专业知识时，要从众多数据中选取能够影响数据稳定性且具有研究价值的属性比较困难，为此引入了“属性隶属度”的概念。它能够反映每个属性的检测价值，即使无领域专家在场的情况下，终端操作人员也能够通过计算每个属性的“属性隶属度”，选取到最适合的检测属性。

属性隶属度μ：对于数据集中任意一条数据ω的任意属性，都有一个数μ(ω)与之对应，μ为该属性的“属性隶属度”，μ(ω)为该属性的隶属度函数，表示为：

(5)

属性的μ(ω)值越大，说明该属性值的波动越大，检测价值也越高，就越有可能成为被检测的对象；μ(ω)值越小，该属性值的波动也越小，检测价值也越低，就越有可能被忽略。

2.2 改进距离度量

为了解决由数据分布不均匀而导致的检测准确率低的问题，文中改进了距离度量，以明考斯基距离为例，表示为：

(6)

其中λk定义为：

(7)

对于分布不均匀的数据集来说，基于常用距离的异常点检测算法的检测效果较差[5-7]，当数据点分别分布在密集区域和稀疏区域时，由k个最近邻点所组成的局部区域范围是不同的，按照传统基于距离的算法进行异常点检测时，就有可能会将原本正常的数据点标记为异常点[8]。

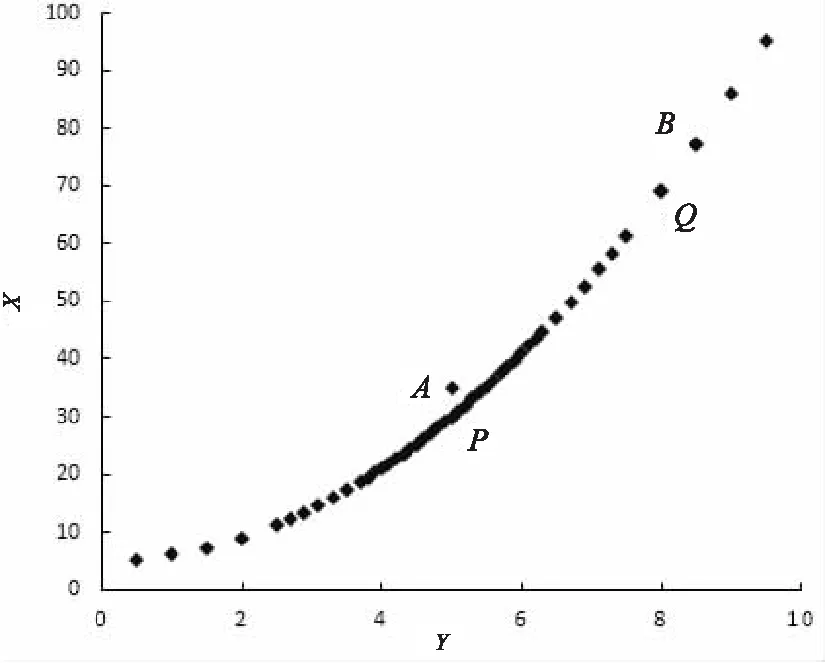
图1 不均匀分布的散点图

图1所示为非均匀分布的抛物线形数据集S，已知点A为数据集S中的一个异常点，点B为数据集S中正常的数据点，若点B到其k个最近邻点的距离之和大于点A到其k个最近邻点的距离之和，传统基于距离的算法就可能会把B点当作异常点来处理，而把点A认为是正常的数据点[9-10]。

2.3 基于改进距离和的异常点检测算法

传统基于距离的算法中，对DB(p,d)的参数设置比较复杂[13]，需要不断进行测试，找出符合用户需求的参数，而所得结果对参数是敏感的。为了避免参数的设置，提出了一种基于改进距离和的异常点检测算法，并且给出了异常点的评价方法。步骤描述如下：

Step1:假设数据已经过标准化，计算数据集中第一条数据与其他数据之间的距离dij。

Step2:由Step1得到该数据点与k个最近邻点的距离之和Di(k)。

对此算法的说明如下：

(2)φi为评价异常点异常程度的关键，即矩阵P中第i行元素之和，φi的值越大，就说明数据点i离其他点越远。即该点比其他点异常。

3 实验设计

实验选取了100组股票交易数据进行异常点检测，每条记录包含6个属性。通过计算每个属性的μ值，最终选择了μ值最大的两个属性即交易量与交易金额。经筛选后的数据集如表2所示。

表2 筛选后的部分数据集

实验中所用的距离度量是选取q=2时的明考斯基距离进行计算，当k=30时，距离和矩阵P为：

由矩阵P可计算出100个φ值，对φ值进行降序排列，设用户期望的异常值为4，则可得到四个异常点，如表3所示。

表3 异常点检测结果

从输出的结果来看，求得的数据点的距离之和按降序排列，则可取前四条记录，即序号为6,35,100,61的数据与其他点距离之和最大，可判定为异常数据。

如图2所示，实验将数据量增加至200,500。并分别对两种算法检测出的异常点个数进行了对比。传统基于距离和算法的检测效果不理想，准确率约为70%；而基于改进距离和的异常点检测算法的准确率可以达到90%以上，取得了较好的检测效果。

图2 算法检测结果对比

4 结束语

介绍了几种基于距离的异常点检测算法和几种常用的距离度量，给出了一种选择检测属性的方法，提出了一种改进的基于距离和的异常点检测算法。该算法舍去了传统算法中对DB(p,d)参数的设置，避免了因参数不合适而产生参差不齐的结果，并给出了数据的异常程度，能够更直观地呈现出来。与传统基于距离和的检测算法进行了比较，证明了该算法在分布不均匀的数据集上有较好的检测效果。现阶段异常点检测技术的难点在于对高维数据的处理方法，因此基于改进距离和的异常点检测算法在高维数据上的应用还有待于进一步研究。