一种引入单纯形法的能量均衡路由算法
2019-03-21汤文兵陈亚楠
汤文兵,陈亚楠,张 牧
(安徽理工大学 计算机工程学院,安徽 淮南 232000)
0 引 言
无线传感器网络(wireless sensor network,WSNs)有由许多廉价并且能进行无线通信的节点组成,具有监测水平高、覆盖面积大、可远距离监控等优点,在军事、医疗或者农业等众多领域应用广泛[1-3]。传感器节点一般部署在非常危险或者无法抵达的地方,网络中节点的能量非常有限,这些节点的能量还不能得到及时的补充,所以节省节点能耗,均衡网络消耗,延长网络的生存周期是无线传感器网络研究的热点。
建立高效的通信路径实现与基站通信是研究无线传感器网络路由算法的重点。文献[4-5]研究了基于LEACH算法的路由协议,解决了传统算法中随机选取簇头的问题,但在均衡网络能量方面有待提高。PEGASIS算法是在LEACH算法的基础上发展而来,该算法采用跟贪婪算法相似的原理生成一条通信路径,随机选取簇头节点实现与基站通信,但未考虑节点的能量问题,使得路径中节点的能量消耗不均衡,导致一些节点过早死亡,影响了网络的生存周期。文献[6]针对该问题提出了解决方案。文献[7]说明遗传算法也能解决路径优化问题,并考虑了节点能量有限的问题,但未考虑寻优过程中簇头选取和收敛速度的问题。以上算法都有其优点,在路径优化的过程中,节点要经过大量的计算,对于能量有限的网络来说,这种优化过程非常受限。针对上述问题,并结合文献[8-15],提出一种遗传算法和单纯形算法的混合算法来均衡网络中节点的能耗,延长无线传感器网络的生存时间。遗传算法的随机搜索特点和单纯形算法的局部寻优和确定性特点互相补充,能加快路径寻优的速度,在寻优中不会陷入局部最优的问题。
1 网络能耗模型
无线传感器网络的能量消耗主要体现在节点与节点之间的通信消耗。提出的能耗模型[16]如下:
发送数据消耗的能量为:
Etransmit(k,d)=k*Eelec+ε*k*d2
(1)
接收数据消耗的能量为:
Ereceive(k)=k*Eelec
(2)
数据融合消耗的能量为:
Efusion(k)=k*EF
(3)
设d为无线传感器网络中节点之间的通信距离,Eelec为节点接收或者发送1 bit数据所消耗的能量,k为发送或接收数据的量(单位为bit),ε为功率放大的能耗系数,EF为融合1 bit数据消耗的能量。那么网络中每个节点所消耗的总能量为:
Eall=Etransmit(k,d)+Ereceive(k,d)+Efusion(k)=2kEelec+k(εd2+EF)
(4)
2 混合遗传算法
2.1 遗传算法(GA)
遗传算法属于进化算法(evolutionary algorithms)的一种,该算法通过模仿自然界的选择与遗传的原理求解最优解。遗传算法与枚举、启发式算法相比,以生物进化为基础,所以具有收敛性强、鲁棒性强、运算计时少和随机搜索能力强等优点。
2.2 单纯形算法(SM)
单纯形算法是指在一个多维空间中构建一个多面体,比较多面体的顶点,找出最好、最差和次优的顶点;通过单纯形中的反射、扩张、压缩等操作获得较优的探索点,然后探索点取代最差点。重复迭代,替换最差点,这样逐渐逼近最优解。设最优点为xb,次优点为xg,最差点为xw,反射点为xr,扩张点为xe,压缩点为xt,收缩点为xf,则有:
反射:xr=xc+θ(xr-xw),θ≤1;
扩张:xe=xe+ρ(xw-xc),ρ>1;
压缩:xt=xc+ϑ(xw-xc),ϑ<1;
收缩:xf=xc-ϑ(xw-xc),ϑ<1。
2.3 混合遗传算法(GA-SM)
单纯形算法是一种局部寻优算法,在一定区域内具有较好的搜索效率。而遗传算法是一种全局寻优算法。通过遗传算法的并行性,分布式计算解空间中的解,从而提高求解的速度。但遗传算法的局部搜索效率不高,会导致相同的节点可能会被搜索很多次,增加了算法的延时,降低了整个算法的效率。单纯形算法能解决遗传算法过早收敛的问题,通过单纯形算法对遗传算法中的节点进行更新操作,缩小算法范围。同样,遗传算法使单纯形走出局部范围内的搜索趋势,所以引入混合遗传算法能均衡全局和局部搜索,高效地寻找最优路径。
2.3.1 算法设计
分布在一定监测区域内的普通节点位置固定不变且能量有限,Sink节点的能量无限。通过广播的方式,Sink节点掌握区域内所有节点的位置和能量信息,广播消耗的能量很小,所以路径优化的工作由Sink节点完成。然后从Sink节点开始广播要形成通信路径的消息,告知网络中的普通节点生成通信链路。
数据链路形成之后,要实现与Sink节点的通信,就需要在链路中寻找一个簇头完成通信。在LEACH算法中,选择小于一个随机数的阈值,作为一轮的簇首节点,在PEGASIS算法中,网络中的节点都能与基站通信,簇首的选择也是随机的,这样增加消耗节点的有限能量,这些节点在一定阶段会出现大量死亡,就缩短了网络的生存周期。簇头的选择既要考虑该节点的剩余能量,保证有足够的能量实现与基站的通信,又要考虑该簇头节点与基站间的距离问题,节点距离较远会消耗过多的能量,增加网络负载。
如果一个节点比较忙碌,那么该节点的剩余能量会相对较少。用τ(vi)表示节点vi的忙碌程度,E0(vi)表示节点vi的初始能量,Eall(vi)表示节点vi在通信过程中消耗的能量。相应公式如下所示:
(5)
设基站用vt表示,那么节点vi到基站vt的距离用dvt,vi表示,有:
φ(vi)=τ(vi)dvt,vi
(6)
即
(7)
链路形成后,可知各节点的φ(vi),选取φ(vi)值最小的节点作为该链路的簇头,实现与Sink节点的通信。
2.3.2 GA-SM算法步骤
(1)产生遗传算法的初始种群。设文中节点的分布范围为100×100,并在该范围内随机生成100个节点,其中Sink节点的位置为(50,150)。为了产生优质的初始种群,减少算法优化的过程,提高算法整体的效率,文中采用路径编码方式,利用均匀分布的伪随机数,在监测区域内生成相对均匀分布的70条路径作为遗传算法的初始种群。
(2)计算个体的适应度值,确定遗传算法是否收敛。适应度函数[13]的选取应考虑该链路的剩余能量和路径消耗这两个方面。路径消耗是指传输信息在传输途中的消耗。通过路径中所有节点的忙碌情况决定该路径的剩余能量,如果路径中多数节点处于忙碌状态,那么该路径整体的剩余能量就越少。即路径X={v1,v2,…,v100}的适应度函数如下:
(8)
其中,α表示影响节点忙碌的权重;β表示影响路径消耗的权重。适应度f的值越小,说明该链路越好,遗传到下一代的可能性就越高。以迭代15次作为遗传算法的收敛条件,如果满足收敛条件,则输出最优结果,否则进行下一步操作。
(3)选择操作。如果遗传算法未结束,就继续执行选择操作。由步骤1产生了70条路径。选择操作采用轮盘赌选择算法。根据公式9决定路径被选中的概率:
(9)
其中,P(i)指路径i被选中的概率;Fi=1/fi,fi指路径i的适应度值。这样P(i)值越大,被选择的概率越大,保证了优良个体能遗传到下一代。

(5)变异操作。取变异概率Pm=0.1,从新的种群中随机选取需要执行变异操作的路径。文中随机选取变异点,然后通过倒序和插入操作实现变异操作。比如X=(v1,…,vk-1,vk,vk+1,…,v100),选取变异点vk,执行变异操作后,X=(vk+1,…,v100,vk,v1,…,vk-1)。变异操作形成一条新的路径,增加了种群的多样性,不陷入局部寻优,有效地避免了遗传算法过早收敛。
若遗传算法未截止,则进入下一轮的步骤3,直到遗传算法收敛条件满足,遗传算法结束,得出一个最优路径和一个种群,进入单纯形算法。
(6)产生单纯形算法的初始种群。已知在无线传感器网络中包含100个节点,那么单纯形算法就要求这100个点形成101条路径方案。遗传算法结束后,产生一个最优解和包含69个解的种群,即仍是70条路径。那么再随机生成31条路径方案和遗传算法的70条路径方案,构成单纯形的初始种群。101条路径作为多维空间中多面体的顶点。顶点的集合为S=(X1,X2,…,X101),集合S中的每个顶点表示一种路径方案。通过式8决定各种路径方案的优劣。用Xb表示最优方案,Xw表示最差方案,Xg表示次优方案,即Xb=minf(Xi),Xw=maxf(Xi)。
(7)选取单纯形算法的质心。质心Xc决定着算法寻找最优路径方案的方向。除最差路径方案外,选取与平均适应度函数值最小的方案作为质心Xc。
(10)
|f(Xc)-fave(t)|<δ,0<δ<1
(11)
(8)反射操作。最差路径方案Xw关于质心Xc做反射操作,做最差方案关于质心的反方向操作,以便能探索空间中各种可行的路径方案。作以质心Xc为圆心,Xc与Xw距离d(Xc,Xw)为半径的圆。在这个圆形区域内存在其他路径方案。找一个与直线XcXw角度γ(0<γ<π)最大的方案。如图3所示,找出一个反射方案Xr。
(9)具体寻优操作。根据反射操作,判断该反射方向是否是产生最优方案的方向。
(a)若f(Xr) 作以反射点Xr为圆心,距离d(Xr,Xc)为半径的圆。在圆形区域内找一个与直线XcXr角度最大作为扩张方案。若f(Xe) (b)若f(Xb) (d)若f(Xr)>f(Xw),说明反射操作不可行。调整寻优方向。除最优路径方案外,其他所有路径方案进行压缩操作。各路径中的点分别作以最优路径中的点为圆心,两点之间的距离为半径的圆,在圆中寻找与这两点夹角最大的点,这些点组成压缩方案Xt。 反射,扩张,收缩方式如图1所示。 图1 单纯算法执行过程 (10)以迭代35次作为单纯形算法的截止条件,如果满足结束条件,则输出最优结果,否则继续执行单纯形算法。 混合算法执行过程如图2所示。 图2 混合遗传算法执行过程 仿真参数如表1所示。 表1 仿真参数 从失效节点的情况、算法收敛速度和能耗三个方面作比较,以体现文中的算法的优越性。 图3给出在不同的通信轮数下,GA、GASM和LEACH三种算法节点失效的情况。LEACH算法的通信轮数达1 000次左右时,大量节点死亡。LEACH算法中簇头的选择没考虑节点能量问题,所以通信轮数越多,失效节点的数目就越多。第一个节点出现死亡时,文中算法的通信轮数达到传统遗传算法的130%。在60%的节点死亡前,文中算法的通信轮数比GA和LEACH算法都多。但在节点死亡数达到90%时,GA的通信轮数和GA-SM差不多,这是因为遗传算法中轮流选择节点作为簇头节点,但此时存活的节点数很少,失去了研究的意义。文中算法结合了单纯形算法和遗传算法,单纯形算法对遗传算法形成的优质种群进行更优的操作,替换路径中能量较少的节点,使路径的通信时间更长,所以GA-SM形成的路径寿命更长,延长了网络的生存周期。 图3 死亡节点对比 GA和GASM算法都进行20次实验,每次实验前网络中节点的分布是随机的,给出每次实验收敛时的迭代次数,如图4所示。 图4 收敛速度 可以看出,GA-SM的收敛速度比GA提高了100%~150%。遗传算法寻优方式是全局寻优,搜索范围很广,所以算法收敛速度相对较慢。而文中算法是在遗传算法的基础上加上单纯形算法,单纯形算法是一种确定性的局部寻优算法,所以该混合算法能加快算法的收敛性,提高寻优的速度并且还能提升算法寻找最优路径的质量。 当网络中出现第一个节点死亡时,实验就结束,GA-SM、GA和LEACH三种算法分布在区域内节点的剩余能量如图5所示。GA-SM算法中剩余能量高的节点数所占的比例很少,这是由于每次迭代时,都会寻找能量较高的探索点代替最差点,考虑了能量因素。GA算法也考虑了节点的能量问题,但剩余能量较多的节点数目比混合遗传算法的多。而LEACH算法生成通信路径时,没有考虑能量问题,所以实验结束时,含有剩余能量多的节点数目远大于GA-SM和GA算法。混合遗传算法有效均衡了节点能量消耗,提高了网络的生存周期。 图5 节点剩余能量分布 文中提出的基于遗传和单纯形混合的能耗均衡路由算法,利用了遗传算法和单纯形算法两者优点寻找全局最优路径,然后优化簇头选择方式,实现节点与Sink节点通信。实验结果表明,与传统的LEACH算法、遗传算法相比,该算法的收敛速度快、网络生存周期长、能耗低,适合节点能量有限的无线传感器网络。

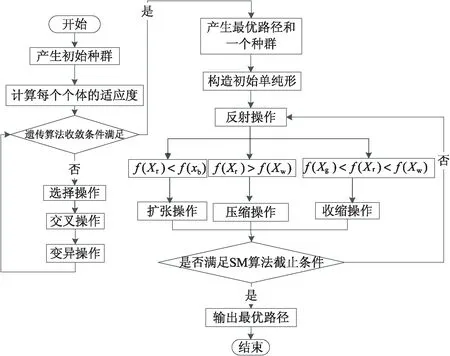
3 实验仿真及分析

3.1 节点失效仿真

3.2 算法收敛速度仿真

3.3 网络能耗仿真

4 结束语
