动态荷载作用下细砂岩流变损伤力学特性试验研究

, 泽佩，，

(1.厦门大学 建筑与土木工程学院,福建 厦门 361005； 2.厦门大学 深圳研究院， 广东 深圳 518057; 3.中建八局第二建设有限公司，济南 250014 ； 4.湖南城市学院 土木工程学院，湖南 益阳 413000)

1 研究背景

软弱岩体的流变特性显著，在地震、爆炸、振动等动态荷载作用下，流变损伤加快，是导致软弱岩体流变损伤破坏并导致严重地质灾害的主要外部动力[1-3]。软弱岩体的破坏过程就是其内部结构微裂纹和微缺陷产生、发展、汇聚、连通的过程，而损伤力学理论将材料视作内部含有各种微缺陷的连续体，研究这些微缺陷的演化过程和材料损伤演化的关系[4-5]。

近年来，越来越多的专家学者将损伤力学理论引入软弱岩体流变变形破坏的研究中。丁靖洋等[6]借助盐岩单轴流变-声发射试验,并基于Weibull分布构建了声发射事件数随加载时间的关系式,进而获得了损伤变量的演化关系式。李夕兵等[7]对含圆形和方形孔洞的花岗岩试样分别进行不同轴向预静载、相同冲击动载下的霍普金森压杆试验,得到花岗岩试样的弛豫时间T2谱曲线、核磁孔隙度和核磁共振图像等特性参数。罗璟等[8]基于疲劳试验,从动力学的角度分析了强震作用下滑坡岩体震裂损伤程度的影响因素。赵延林等[9]基于岩石蠕应变的内涵进行分类研究，提出岩石黏弹塑性应变分离的蠕变试验方法和数据处理技巧。本文以软弱砂岩为研究对象，利用RLW-2000M型三轴流变试验机，研究动态荷载作用下软弱砂岩的动态流变损伤特性、工程特性及变形破坏机制。研究成果对于防治岩土工程地质灾害、确保我国重点基础工程建设安全有重大理论和实际意义。

2 试验方案与试验过程

2.1 试验方案

以软弱砂岩为研究对象，利用RLW-2000M三轴流变试验机研究了软弱砂岩在动态荷载作用下的动态流变损伤特性。试样为Φ50 mm×100 mm(直径×高)圆柱体细粒砂岩，属于陆源细粒碎屑沉积岩，粒径为0.1～0.5 mm，主要成分为石英、长石、燧石和白云母等。RLW-2000M型三轴流变试验设备见图1。

图1 RLW-2000M岩石三轴流变试验机Fig.1 RLW-2000M rock triaxial creep testing machine

试验过程中保持围压10 MPa不变，采用呈正弦变化的动荷载加载，直至试样发生破坏。根据试验结果，研究分析动载幅值、动载频率对砂岩试样轴向流变特性曲线、轴向应力-应变曲线、轴向流变变形、径向流变变形、轴向流变变形滞回圈曲线等影响特性；选取轴向应变为损伤变量，推导计算损伤度表达式，并研究各因素对损伤度的影响特性。

为确定试验最大加载峰值，先进行砂岩的全应力-应变曲线测试，试样破坏时峰值强度约为242 kN，为保证砂岩在一定的流变时间后能发生破坏，取砂岩三轴压缩破坏峰值强度的70%作为设置最大轴向荷载的参考依据。4级轴向荷载区间分别设置为：F1-2=70～120 kN;F3-4=90～140 kN；F5-6=110～160 kN；F7-8=130～180 kN。动载频率从低到高设定4个级别，考虑到每一级轴向荷载的变化范围较大，并结合试验设备的实际情况，频率不宜设置较高，通过试验探究，将4级频率分别设置为0.008，0.010，0.020，0.050 Hz，试验方案的主要参数见表1。

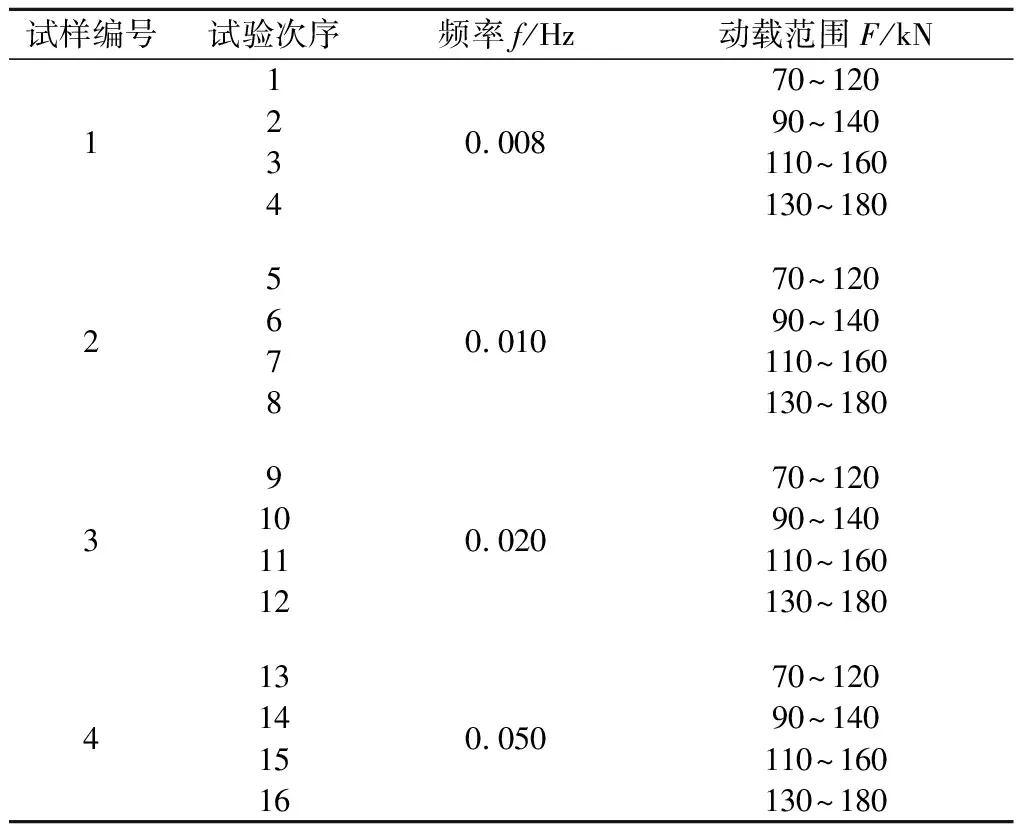
表1 试验方案主要参数Table 1 Main parameters of testing scheme

2.2 试验过程

试验采用RLW-2000M三轴流变试验机。该试验装备能够完成各种岩石在复杂环境(如动应力场、渗流场、温度场)下的单轴压缩试验、动三轴压缩试验、水渗透试验、岩石流变试验、加卸载试验以及松弛试验等。该设备的软件部分由在Windows系统下运行的test软件控制，该软件控制功能齐全，能够在试验过程中自动记录数据并将各变量之间的对应关系以图像的形式显示出来。

根据国际岩石力学学会的试验标准，砂岩试样制备过程分为钻芯、切割、打磨和筛选4个步骤，制备尺寸为Φ50 mm×100 mm标准圆柱砂岩试样。试验前用游标卡尺量测试样的直径、高度。试验过程为：打开电脑设备、控制柜和电控箱；安装试样；加围压、轴压试验；当试样破坏或达到方案设定的条件后，结束试验。开始卸载及卸样。

图2 试样破坏后的形态Fig.2 Morphology of testspecimens after damage

3 试验结果分析

3.1 各试样轴向流变变形曲线

试样大致呈剪切状破坏，其裂纹与环向呈一定的角度，且试样的表面有多条主裂纹，如图2所示。不同频率条件下正弦动载作用下各试样的轴向流变变形随时间的变化关系曲线如图3所示。

由图3可以看出：试样在第1级、第2级、第3级动载作用下经过短时间的减速流变后变形达到稳定状态，并进入稳态流变阶段。在最后一级动载作用下，试样的流变呈现明显的加速阶段，试样发生破坏。试样在前3级动载作用下产生的变形较小且增长缓慢，而试样在第4级动载作用下的变形增量相比前3个阶段有明显的增大。

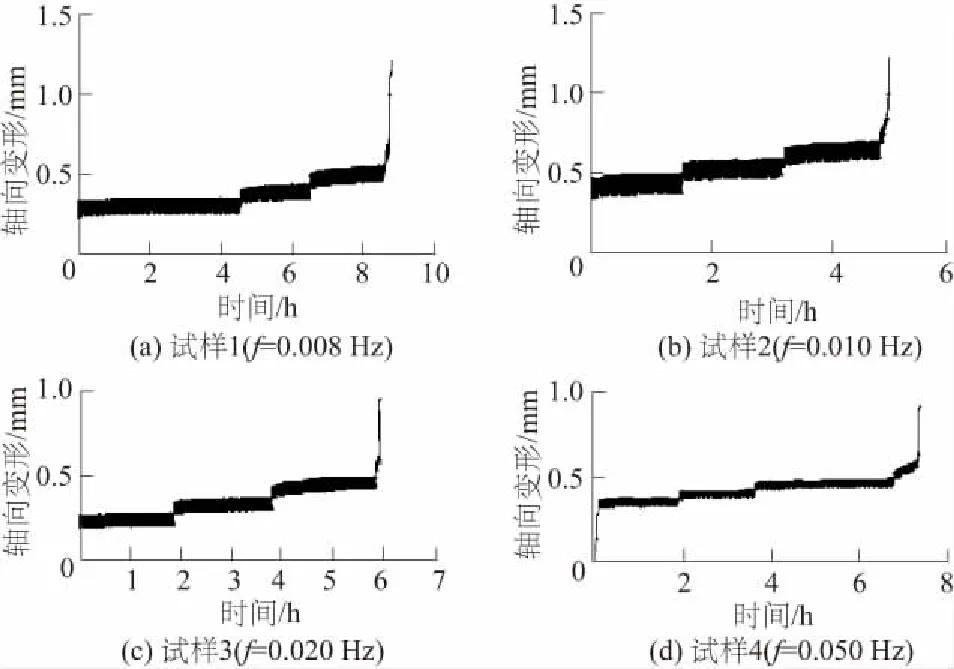
图3 试样轴向流变变形与时间关系曲线Fig.3 Curves of axial deformation against time under varying loading frequency

3.2 试样各阶段轴向动应力-应变曲线

1—4号试样各个阶段轴向动应力-应变曲线如图4所示。

试样在第1级、第2级、第3级动载作用下，初期的几个滞回曲线较为松散;而随着动载的不断作用，滞回曲线逐渐变得稠密起来，表明试样经过短时间的减速流变后进入稳态流变阶段，试样的应变速率在减小，但滞回曲线一直朝着应变增加的方向偏移，反映了试样应变在逐渐增加，其不可逆的塑性应变也逐渐累积。试样各阶段每条滞回曲线的加载段和卸载段不会重合，而是形成一个闭合的环状，反映出砂岩试样在试验过程中明显的弹塑性特征；当试样在第4级动载作用下即将破坏时，试样的滞回曲线由稠密逐渐变得稀疏，且最后几个滞回曲线在应力变化不大的情况下，应变却发生显著的增大，这说明试样已经开始出现加速流变阶段。随着动载范围的增大，各阶段滞回曲线所围面积呈增大的趋势，能量耗散逐渐增大，试样的损伤在不断累积。

3.3 动载大小对试样轴向、径向变形的影响

根据试验测试数据和相关曲线算出试样各阶段的轴向、径向变形增量大小，可以得到试样各阶段变形增量随动载大小变化的曲线，如图5所示。

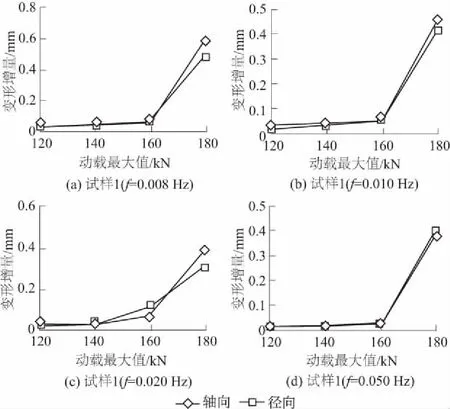
图5 试样变形增量-动载最大值变化关系曲线Fig.5 Relationship of axial and radial deformation increments against maximum dynamic load

由图5可以看出:对于同一试样，在相同的动载频率作用下，试样的轴向、径向变形增量大致随着动载的增大而增大。各试样在前3级动载的作用下，其轴向、径向变形增量增加的幅度并不大，这是由于试样在前3个阶段并没有发生加速流变，试样经历短时间的初始减速流变段后进入稳态流变，变形也趋于稳定；试样在最后一级动载作用下，变形增加较大并进入加速流变阶段，轴向、径向变形增量有较大幅度的增加。总体来说，动载的增大使试样的流变特性更为明显，试样的损伤逐渐加大，塑性变形增大，最终导致试样发生破坏。

3.4 动载频率对轴向、径向变形的影响

在相同动载作用范围、不同动载频率作用下，试样的轴向、径向变形增量随动载频率的变化关系曲线如图6所示。

图6 试样变形增量-频率变化关系曲线Fig.6 Relationship of axial and radial deformation increments against dynamic load frequency

由图6可以看出：当动载的范围一定时，试样的轴向、径向变形增量大致随着频率的增大呈减小的趋势。这是由于在低频的动载作用下，随着动载频率的增加，试样更易趋于密实状态，使得试样可压缩的变形量减少，且发生不可恢复的塑性变形速率减小，试样的流变特性在高频动载下也表现得不显著。

4 动态流变损伤特性研究

4.1 损伤变量的选取

砂岩试样在循环荷载作用下的变形也呈周期性变化。假定试样在损伤演化过程中每一个循环的损伤是不变的，基于此假定可以研究循环荷载上限应力作用时刻所对应的试样损伤状态的发展演化，在循环荷载的作用下上限应力所对应的试样损伤状态的发展演化就代表了砂岩试样的损伤演化过程。具体的砂岩损伤度公式推导如下[10-11]。

砂岩一维损伤本构方程为

(1)

两端对ε求导可得

(2)

式中：D为岩体的损伤度；E为无损伤岩体的弹性模量(MPa)；ε为第一周循环荷载上限应力所对应的应变，此时试样没有损伤；σ为应力(MPa)。对式(2)两端求积分得：

(3)

(4)

将初始条件ε=ε0时D=0，ε=ε′时D=1代入式(4)得

(5)

式中：ε′为最后循环荷载上限应力所对应的应变，此时试样完全损伤；C为积分常数；ε0为初始应变。

4.2 动载频率对损伤度的影响

试样的损伤度随时间的变化规律曲线可以由试验数据处理后得到。不同动载频率下试样的损伤度随时间的变化关系曲线如图7。

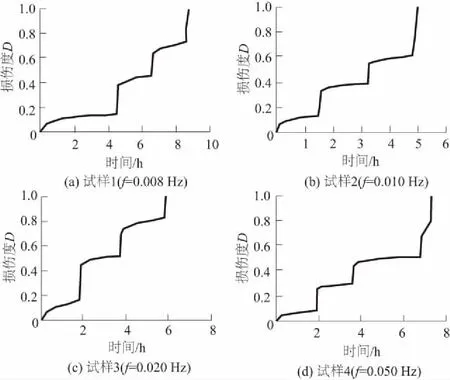
图7 不同频率作用下试样损伤度变化曲线Fig.7 Variation of damage degree against time undervarying dynamic loading frequency

由图7可以看出，各个试样的损伤度随着时间的增加而逐渐增大，各试样在第1级分级荷载作用下损伤度的增加幅度不大，这是由于试样在开始阶段有一个逐渐被压密的过程，试样的损伤还很小。各试样的损伤度在增加动载作用范围后会有一个突变，随后又趋于稳定，损伤度的变化速率也有一个先衰减后稳定的过程，这与试样的变形曲线类似。随着动载的不断增大，试样的损伤表现得也越来越明显，当动应力水平达到并超过试样的屈服应力以后，试样的损伤出现了加速增大的现象直至试样发生破坏。

5 结 论

本文对动应力场作用下软砂岩流变损伤特性进行了试验研究，主要得到以下结论：

(1)分级加动荷载作用下软弱砂岩的流变与静荷载作用下相同，流变曲线特征符合流变演化的3个阶段。随着动荷载的逐级加载，试样的流变变形呈增大的趋势，随着变形的累积，试样在第4级动载作用下的变形增量相比前3个阶段有明显的增大，直至发生加速流变破坏。

(2)试样在加载过程中，各阶段每条滞回曲线的加载段和卸载段不会重合且形成一个闭合的环状，滞回曲线的形状大致呈斜扁状，动载作用下试样各阶段的滞回曲线面积随着动载幅值的增大有被拉大的趋势，当试样加载到即将破坏时，试样的滞回曲线由稠密逐渐变得稀疏。滞回环的形状大致随着频率的增大越来越扁，滞回圈所围的面积也逐渐减小。

(3)当动载作用范围一定时，随着动载频率的增大，在相同的时间内动载振动次数增加以消耗更多的能量，试样更易趋于密实状态，导致试样的轴向变形增量和径向变形增量随着频率的增大呈减小的趋势，这与随着动载幅值的增大而增大的趋势相反。

(4)试样的损伤度在增加动载作用范围后会先突变随后又趋于稳定，随着动载的不断增大，试样的损伤表现得也越来越明显，当动应力水平达到并超过试样的屈服应力以后，试样的损伤出现了加速增大的现象直至试样发生破坏。