基于BP神经网络的MIKE SHE模型参数率定

，，，

(河北农业大学 城乡建设学院，河北 保定 071000)

1 研究背景

随着遥感和GIS技术的蓬勃发展，分布式水文模型在水资源规划、管理中发挥着越来越重要的作用。然而，模型从研究到应用仍然面临着重大的难题：一方面是模型自身结构的构建；另一方面是模型参数的率定[1]。MIKE SHE是丹麦水工试验所DHI开发的基于物理过程的分布式水文模型。模型包含参数较多，尽管各个参数均具有比较明确的物理意义，但是根据其物理意义直接确定参数取值也有较大的困难，参数不完全独立，往往表现出不确定性、高维度和高度非线性的特点。对于MIKE SHE模型，国内的研究相对较晚，主要集中在模型在不同地区的适用性研究和流域径流过程、地下水位变化的模拟，对模型的参数率定方法的研究较少[2-5]。模型参数取值的准确与否直接影响模型输出结果的准确性。目前在分布式水文模型的参数率定中，应用较多的是面向全局优化的遗传算法(GA)、SCE-UA算法、贝叶斯方法、RSA方法和GLUE方法。它们一般考虑水量平衡、确定性系数、洪峰和枯水流量过程，不断调整各个参数使得模型的输出值尽可能地接近实测数据资料[6]。在调整过程中，花费的时间较多且受人为因素影响较大。因此希望找到一种直接利用历史实测水文资料来反求模型参数的方法，就是所谓的模型参数反演分析。BP神经网络是一种多层前馈神经网络，具有较强的非线性映射能力、自学习和自适应能力及高速寻找优化解的能力，广泛应用于参数反演分析中[7]。因此，本文以MIKE SHE模型为基础，应用BP神经网络映射模型输出与参数之间的非线性关系，提出一种反分析率定模型参数的方法，并且通过与模型参数自动率定结果比较，验证了该方法的准确性。

2 MIKE SHE模型参数反演方法

2.1 MIKE SHE模型原理

MIKE SHE模型通过数值分析建立相邻网格之间的时空关系，能够模拟蒸散发、地表径流(包括坡面漫流和河道流)、非饱和带水流、饱和带水流、融雪、溶质和泥沙输移等水文过程以及它们之间的互相作用。在模拟过程中，流域在水平方向被划分为若干大小相同的矩形网格，并将它们赋予不同参数，使模型参数的空间分布更符合实际；在垂直面上，模型划分成坡面流、河道水流、非饱和带水流、饱和地下水4个水平层，易于分析各层之间土壤水的运动规律[8-9]。

2.2 MIKE SHE模型参数反演步骤

用BP神经网络对MIKE SHE模型参数进行反演分析，即：首先用MIKE SHE模型计算各待反演参数在不同水平组合下的流量、水位，得到一组可用于训练网络的样本；然后，以MIKE SHE计算结果作为神经网络的输入，以待反演的参数作为输出，建立BP神经网络；其次，对网络进行训练，当满足精度要求后停止训练，此时，BP神经网络已经建立从径流、水位到待反演参数的非线性映射；最后，将实际观测的流量、水位输入经过训练的BP神经网络，经网络计算后可得出对应的反演参数值。这时，把反演参数值重新代入MIKE SHE进行模拟计算，验证反演结果的可靠性[10]。BP神经网络应用于MIKE SHE的参数反演，训练样本的数量和质量直接影响神经网络的可靠性和准确性，在设计过程中引入均匀设计法，在较少的试验次数下，可以保证计算精度。基于均匀设计和BP神经网络的MIKE SHE模型参数反演的具体实现过程见图1。

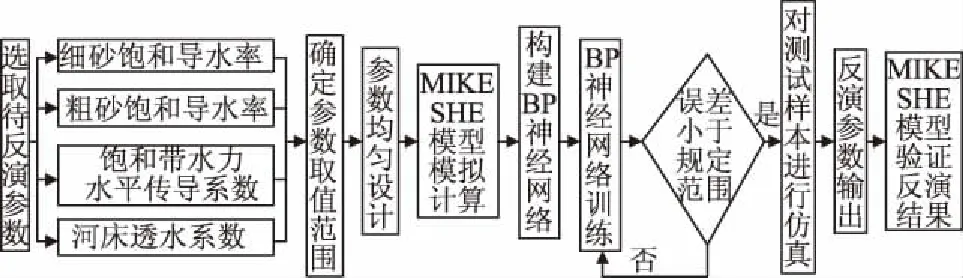
图1 MIKE SHE模型参数反演流程Fig.1 Flowchart of parameter inversion of MIKE SHE model

3 MIKE SHE模型参数反演在Karup流域的应用

3.1 研究区域概况

Karup流域是位于丹麦西部的一个典型的冲积平原，面积为440 km2。流域土地利用方式分为4类，以林地和灌溉作物为主，兼有少量的灌木和湿地；土壤类型以砂性土壤为主；其含水层主要是冰川沉积物，集水区地势平缓。研究区不饱和带深度从地下水深25 m的东部开始变化[11-12]。本文主要研究该流域的Karup河流、Haderup河流和Hauge Creek河流，河网水系如图2所示。

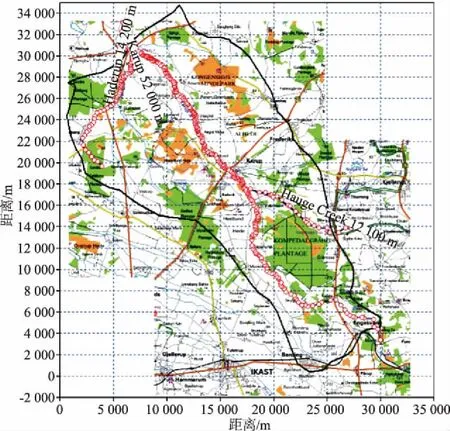
图2 Karup流域Fig.2 Map of the Karup watershed

3.2 模型构建

MIKE SHE模型的建立需要DEM高程、降雨量、蒸散发量、土地利用类型分布、土壤属性等数据资料，本文以文献[13]提供的数据资料为基础建立MIKE SHE模型。模型将Karup流域划分为500 m×500 m的网格。降雨量采用流域内9个雨量站记录的6 a(1970—1975年)降雨资料。流域划分为4类不同的植被区，分别为耕地、林地、灌木和湿地。模型中对于坡面流采用圣维南方程近似扩散波，并用有限差分法对方程进行求解；不饱和水流采用Richards方程计算；饱和带水流的计算运用Successive Overrelaxation Solver(SOR)进行。

3.3 参数均匀设计

选取饱和导水率、饱和带水力水平传导系数和河床透水系数为待率定参数。Karup流域主要为砂性土壤，饱和导水率有粗砂和细砂之分，各参数取值范围见表1。依均匀设计表U31(3110)对应的均匀设计使用表设计参数，具体数值如表2所示。通过MIKE SHE模拟不同参数方案的流量、水位，将基于参数均匀设计的MIKE SHE计算结果记为模型的理论值，如表3所示。

表1 参数及其取值范围Table 1 Value ranges of parameters

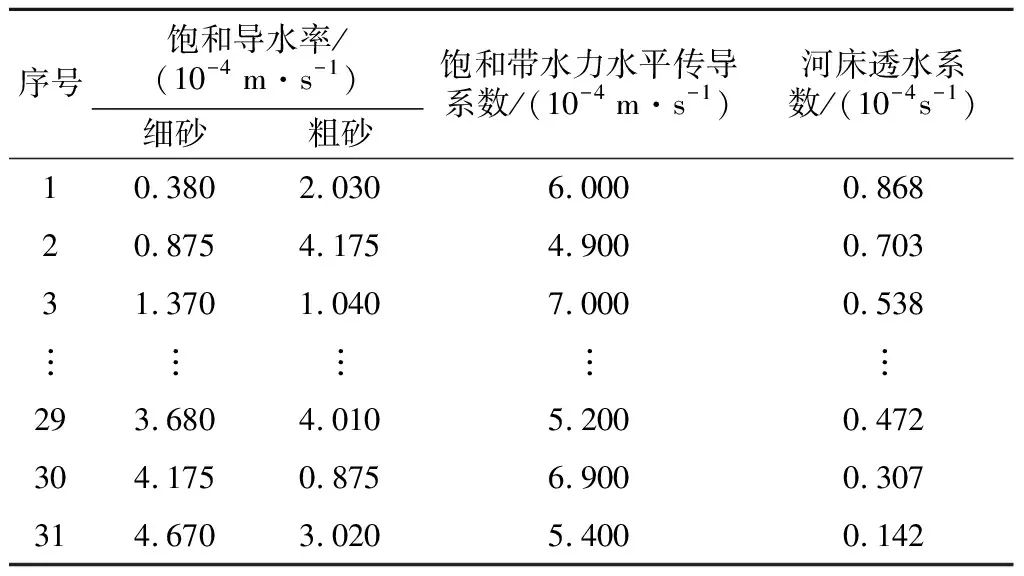
表2 基于均匀设计的参数方案Table 2 Parameter schemes based on uniform design

3.4 模型参数反演

分别将表2和表3中的数据归一化，以对应参数均匀设计方案的MIKE SHE模型理论值——日均流量和日均水位作为输入，参数方案为输出，建立含有1个隐含层的BP神经网络。隐含层单元数的确定参考式(1)，即

(1)

式中：n1为隐含层单元数；n为输入单元数；m为输出单元数；a为[1，10]之间的常数[14]。根据式(1)，依次从最小单元数n1_min=5开始到最大单元数n1_max=15训练网络。当隐含层单元数n1=10时，网络训练达到目标误差，网络训练结束。隐含层10个神经元，网络结构为6-10-4，传递函数为tansig。输出层传递函数为pureline。BP神经网络结构如图3所示。网络中选取前28组数据进行学习训练，达到要求精度后，选用后3组数据为测试样本检验训练效果。3组测试样本的最后输出见表4。

表3 对应参数均匀设计方案的MIKE SHE模型理论值Table 3 Theoretical values of MIKE SHE model foruniform design of corresponding parameters

图3 BP神经网络结构Fig.3 Structure of BP neural network

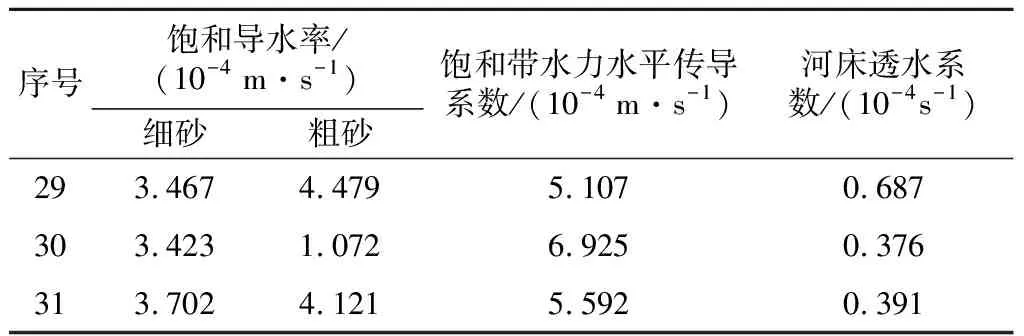
表4 基于BP神经网络的参数反演值Table 4 Results of parameter inversion based onBP neural network

MIKE SHE参数自动率定包括2种方法：Shuffled Complex Evolution(SCE)和Population Simplex Evolution(PSE)。PSE算法是一种全局优化算法，适合在自动校准时系统仿真的并行计算，该方法利用单纯形法中包含的反射和收缩算子来演化种群点[15]。选择PSE算法对3组测试样本进行参数自动率定。算法中参数的取值如图4所示，MIKE SHE参数自动率定结果见表5。

图4 MIKE SHE参数自动率定Fig.4 Automatic parameter calibration ofMIKE SHE model

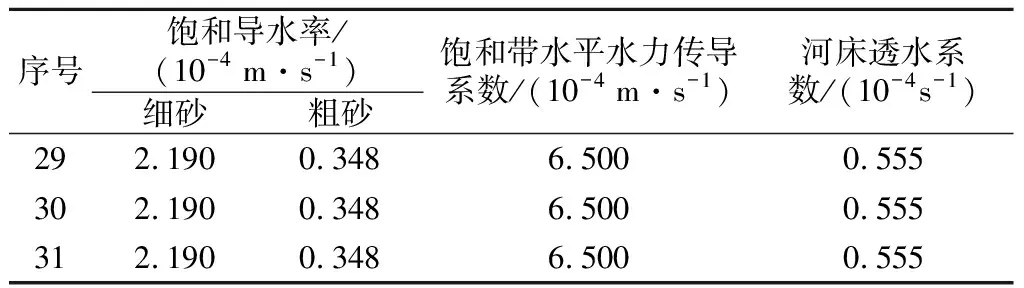
表5 基于MIKE SHE的参数自动率定值Table 5 Results of automatic parameter calibrationof MIKE SHE

表6基于BP参数反演及MIKESHE参数自动率定的流量、水位计算结果对比
Table6ComparisonofdischargeandwaterlevelresultsbetweenBPparameterinversionandautomaticcalibrationofMIKESHE

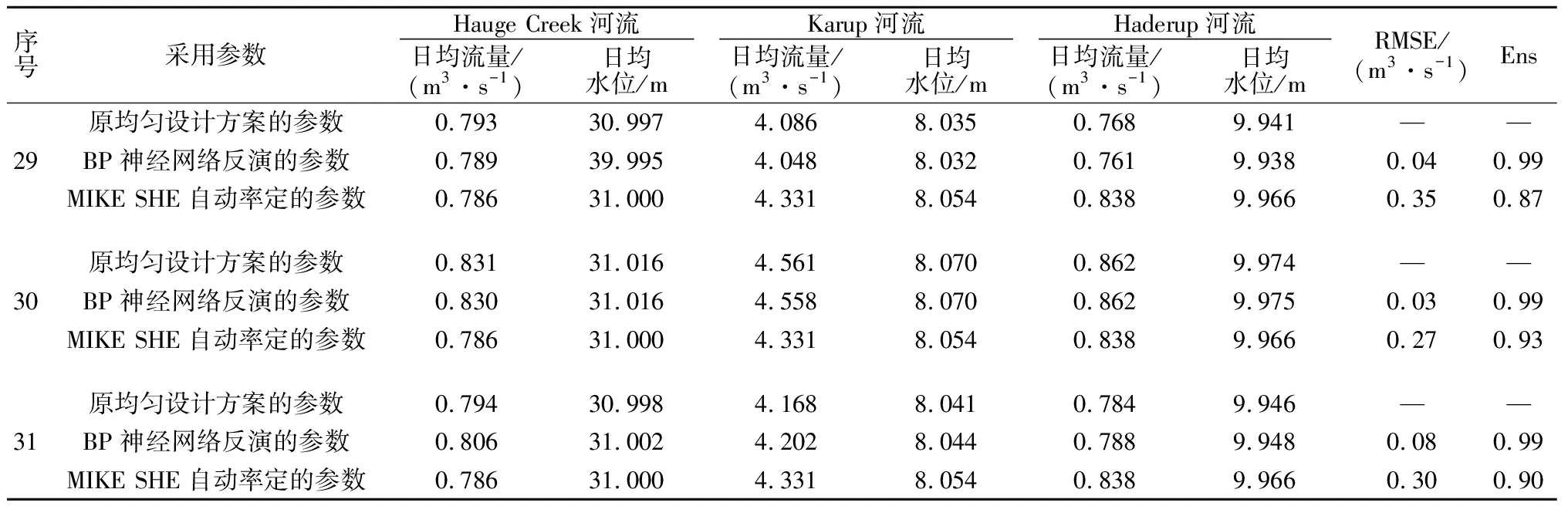
序号采用参数Hauge Creek河流Karup河流Haderup河流日均流量/(m3·s-1)日均水位/m日均流量/(m3·s-1)日均水位/m日均流量/(m3·s-1)日均水位/mRMSE/(m3·s-1)Ens原均匀设计方案的参数0.79330.9974.0868.0350.7689.941——29BP神经网络反演的参数0.78939.9954.0488.0320.7619.9380.040.99MIKE SHE自动率定的参数0.78631.0004.3318.0540.8389.9660.350.87原均匀设计方案的参数0.83131.0164.5618.0700.8629.974——30BP神经网络反演的参数0.83031.0164.5588.0700.8629.9750.030.99MIKE SHE自动率定的参数0.78631.0004.3318.0540.8389.9660.270.93原均匀设计方案的参数0.79430.9984.1688.0410.7849.946——31BP神经网络反演的参数0.80631.0024.2028.0440.7889.9480.080.99MIKE SHE自动率定的参数0.78631.0004.3318.0540.8389.9660.300.90

3.5 模拟结果分析与讨论

将3组测试样本的BP神经网络参数反演值分别输入到MIKE SHE，计算河流的流量、水位，同时将参数自动率定的结果也输入到MIKE SHE进行模拟。本文以Karup河流的均方根误差RMSE(式(2))、模型效率系数Ens(式(3))评价模型模拟性能。其中，RMSE越小，Ens越接近于1，表明模拟效果越好。MIKE SHE的模拟结果如表6所示。

均方根误差：

(2)

模型效率系数：

(3)

从表6中可以看出，3组测试样本，采用BP神经网络反演率定的参数值时，模型的均方根误差RMSE分别为0.04，0.03，0.08 m3/s，模型效率系数Ens均为0.99；采用MIKE SHE自动率定的参数值，RMSE分别为0.35，0.27，0.30 m3/s，Ens分别为0.87，0.93，0.90。RMSE较小、Ens较接近于1的均为基于BP反分析参数，表明BP神经网络参数反演模型与MIKE SHE参数自动率定模块相比，具有更高的准确性。以第29组测试样本为例，在1970—1975年期间Karup河流日均流量的理论值为4.086 m3/s；基于MIKE SHE参数自动率定的MIKE SHE模拟日均流量为4.331 m3/s，RMSE为0.35，Ens为0.87；基于BP神经网络参数反分析的MIKE SHE模拟日均流量为4.048 m3/s，RMSE为0.04，Ens为0.99。从图5(a)可以看出，Karup河流的逐日径流过程线模拟值均与基于参数均匀设计方案的理论径流过程线拟合较好，模型从整体上较好地再现了径流逐日的动态变化过程；但是从峰值上看，基于BP神经网络参数反分析的模拟结果更接近理论值。从图5(b)的年径流来看，基于BP神经网络参数反分析的模拟径流年际动态变化过程与理论径流曲线拟合更好。

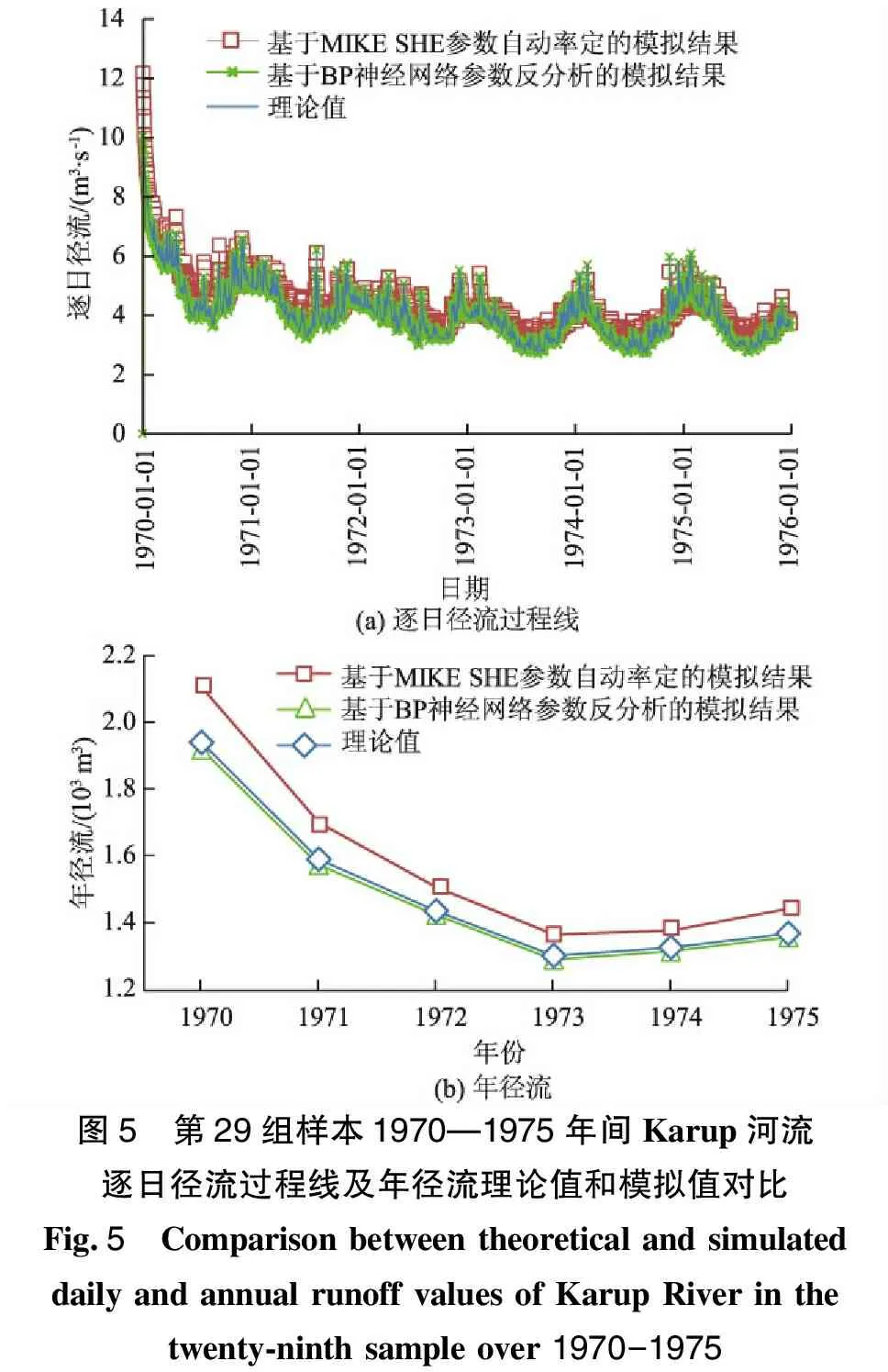
图5 第29组样本1970—1975年间Karup河流逐日径流过程线及年径流理论值和模拟值对比Fig.5 Comparison between theoretical and simulateddaily and annual runoff values of Karup River in thetwenty-ninth sample over 1970-1975

4 结 论

(1)本文以丹麦Karup流域为例，通过BP神经网络反分析方法率定了MIKE SHE的饱和导水率、饱和带水力水平传导系数和河床透水系数，3组测试样本的均方根误差RMSE分别为0.04，0.03，0.08 m3/s，模型效率系数Ens均为0.99，取得了较好的模拟效果，说明该方法用于MIKE SHE模型参数率定是可行的，为MIKE SHE模型的建立和应用奠定了基础。

(2)与MIKE SHE参数自动率定相比，基于BP神经网络参数反分析率定的模拟结果均方根误差RMSE更小，模型效率系数Ens更接近于1，说明基于BP神经网络的参数反演率定方法比MIKE SHE参数自动率定具有更高的准确性，该方法具有一定的推广价值。

(3)本文以基于参数均匀设计方案的MIKE SHE模拟结果作为理论值，与基于不同的参数率定方法的模拟结果进行对比分析讨论，验证了基于BP神经网络的参数反分析率定方法的准确性。在今后研究中，将进一步以实测水文资料为基础对MIKE SHE的参数进行反演率定。