台阶式溢洪道渐缩泄槽水深计算方法

，，

(1.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学 水利水电学院，南京 210098； 3.河海大学 水文水资源学院，南京 210098)

1 研究背景

水库大坝建设的目的是兴利除害，合理控制水流，防止洪涝、干旱灾害发生。泄水建筑物可以合理控制下泄流量，保证水资源的最优利用，当汛期上游来水过大，泄水建筑物将多余洪水宣泄到下游，对水库及大坝的安全运行起到了重要作用[1]。光滑溢洪道摩阻力小，水流下泄时，落差越大流速越大，当流速超过一定范围时，会造成泄水建筑物空蚀破坏，冲刷下游河床，需要设置掺气、消能措施。而台阶式溢洪道通过特殊的形状和消能机理可使下泄水流沿台阶式泄槽逐级掺气、减速、消能，比通常的光滑溢洪道的消能率高出40%～80%，并且能减小工程投资，改善下游冲刷[2]。

目前，国内外学者已经做了很多的试验和计算来分析台阶式溢洪道的水力特性，包括泄槽内最大水深计算、泄槽末端最大流速计算、整体消能率计算、泄槽内各点的压强分布等，验证了台阶式溢洪道具有广阔的应用前景[3-7]。但是台阶式溢洪道台阶的尺寸多样化，并与不同泄槽坡度互相组合，情况复杂，使得对其的研究没有统一的、公认的计算方法和规范。在此情况下，Chanson[8]经过反复试验提出了等宽泄槽台阶式溢洪道的水力计算公式——昌桑法，计算精度高，被众多学者借鉴研究。但由于工程布置的需要以及下游地质条件复杂，无法保证沿程为等宽矩形断面，泄槽需要作一些改动，因此，渐缩式矩形断面泄槽可能出现。渐缩式矩形断面会造成泄槽内出现棱形波，在两侧边墙处出现壅水，使得水面线较等宽矩形断面情况下的水面线要高。参考文献[8]可知，昌桑法并没有考虑台阶式溢洪道在变截面泄槽中的水力特性。昌桑法大多运用于等宽式泄槽，由于壅水因素的影响，无法在渐缩式泄槽中直接计算。所以本文在介绍台阶式溢洪道基本概念和应用现状的基础上，通过对某水库台阶式溢洪道水力学物理模型试验和数值计算结果进行对比，提出了一种改进系数法，对渐缩式台阶溢洪道的泄槽水深模拟作了研究分析。

2 台阶式溢洪道理论分析

2.1 流态分析

工程实践表明，当库水位较低，下泄流量不大时，水流从一级台阶跳跃式跌落到下一级台阶，与台阶发生碰撞，能量降低；当库水位较大时，台阶尺寸相对于下泄水流较小，可以看作增加了泄槽内的“表面粗糙度”，在台阶内还有小的漩滚水流，水流与台阶和漩滚水流摩擦，再加上自动掺气效果显著，水流能量明显降低。而且台阶独特体型使水流在下泄时自动掺气，可以避免溢洪道的空蚀破坏。显著的消能与掺气效果使台阶式溢洪道广受关注。

台阶式溢洪道的水流流态可分为跌落水流、过渡水流和滑掠水流3类[9-12]。

2.2 消能原理与计算原理分析

跌落水流容易出现在泄槽坡度较缓、库水位不高、单宽下泄流量较小时，此时各级台阶稳定跌水。一般水流从第一级台阶水平射出时，水舌下缘出现空腔，水流在空中与气体混掺，回落时携带大量气泡，与台阶面碰撞时，水流四散，互相干扰，能量被消耗[13]；台阶上一定条件下会发生水跃和挑射水流。因为每一级台阶都能发生碰撞，所以下泄水流的势能逐级减小，水流之间的碰撞和水跃产生的旋涡以及挑射时的掺气也能消减一部分能量。跌落水流通过台阶上水流碰撞、水和气体混掺、并形成小型水跃来进行消能，其中的射流在空中扩散破碎，从而消减能量[14]。

当库水位较高时，单宽下泄流量较大，泄槽坡度较大时，容易发生滑掠水流[15]。水流下泄时，起初水深减小，台阶面内出现稳定水平涡流，其他大部分水流以台阶凸角连成的线为假想底面从台阶边缘掠过，称之为主流，主流与台阶和涡流摩擦及剧烈的剪切紊动作用，以此来消耗下泄流量蕴含的能量。此外，下泄主流到某一位置开始掺气，水流紊动，形成掺入气泡的“白水”。经过短暂的过渡阶段，到达均匀掺气断面，该断面以下均匀掺气，水深保持一个稳定的范围。 从初始掺气点开始，泄槽的自动掺气效果使水流中有大量气泡，在水流碰撞摩擦的基础上，加速水流紊动，大大降低水流流速，消能率能达到50%以上[16-18]。本文主要研究滑掠水流，滑掠水流如图1所示。

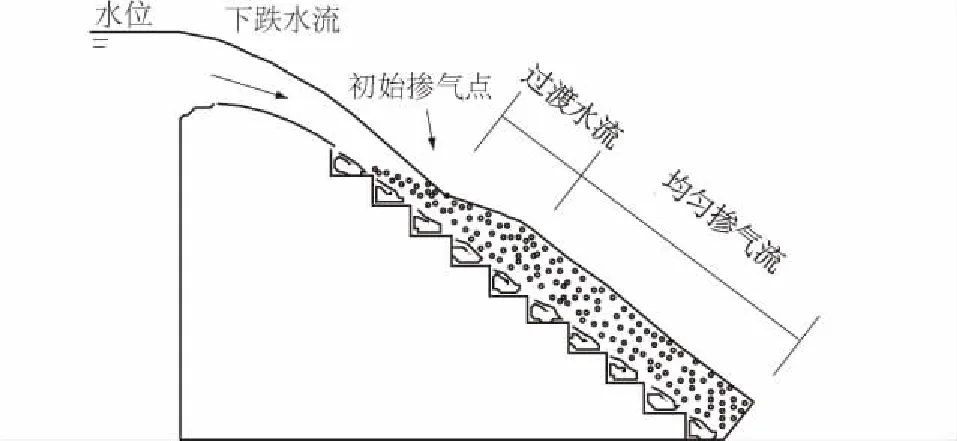
图1 滑掠水流示意图Fig.1 Schematic diagram of gliding flow

而过渡水流流态不稳定，跌落水流与滑掠水流交替、无规则出现，特征不明显，在设计中应避免出现。

Chanson法将台阶视为糙体，在糙体的作用下形成均匀掺气水流。水流下泄，刚开始由于落差，水位下降，水流到达初始掺气点时，开始掺气，水深增加。初始掺气点处水深最低，由于在此位置水流开始掺气，该断面后水深慢慢增加，所以初始掺气点所在的断面属于特征断面。Chanson给出了该断面位置的计算公式，概念由按紊流边界层的理论确定[8，19]。经过一个短暂的过渡阶段，水流均匀掺气，水深保持稳定范围内波动。因此开始进入泄槽时的水深与均匀掺气点时的水深为较大水深，应以此作为边墙高度的参考值。昌桑法详细计算过程见文献[11]。

3 渐缩式泄槽水深计算方法

对台阶式溢洪道的计算到目前为止仍没有公认的、统一的计算规定，考虑到Chanson[8]提出的公式是经过反复试验后得出的，具有一定的可靠性,本文以此方法为基础，研究台阶式溢洪道渐缩式泄槽水深的计算方法。试验发现，在光滑溢洪道上配置渐缩式矩形断面的泄槽时，不仅泄槽内出现棱形波，在泄槽结束处鼻坎前部，棱形波交汇，形成水冠，水深瞬间加大，威胁建筑物安全。但在台阶式溢洪道中配置渐缩式矩形断面泄槽，斜槽尾部水深虽有增加，但远小于光滑溢洪道，消能效果显著且适用于复杂地形。

使用昌桑法可以算出初始掺气点的位置及该位置的水深、流速，均匀掺气点的位置及该位置的水深、流速，但未考虑断面变化的影响。经过参考光滑式溢洪道泄槽水面线计算方法及渐扩式矩形断面消力池自由水跃共轭水深计算公式[20]，并通过大量计算和试验结果发现，昌桑法计算出的断面水深与渐缩式台阶溢洪道泄槽中心水深相差不大，中心水深与两侧边墙处的水深存在对应关系，与泄槽初始断面宽度和结束断面宽度有关。本文在昌桑法的基础上算出特征断面的泄槽断面中心水深之后，乘以系数得到两侧边墙处的水深，此系数为泄槽初始断面宽度和泄槽末尾断面宽度比值的3/7次方。在计算特征断面时，特征断面的位置也会受到渐缩式泄槽内壅水的影响，也需要乘以一个系数折减，此系数为泄槽末尾断面宽度和泄槽初始断面宽度比值的1/7次方。当泄水建筑物为渐缩台阶式溢洪道时，此改进系数法可计算泄槽两侧边墙处的水深，便于确定边墙高度，有利于溢洪道的安全运行。

3.1 流态判定

Chanson认为出现跌落水流的临界值条件为

(dc/h)c=0.091 6(h/L)-1.276。

(1)

式中：dc为临界水深(m)；h为台阶步高(m)；L为台阶步长(m)。

式(1)成立条件为0.2≤h/L≤6，即当dc/h<(dc/h)c时出现跌落水流流态。而随着流量或坡度的加大，Chanson提出的滑掠水流流态的临界值为

(dc/h)c=1.057-0.46h/L。

(2)

即当dc/h>(dc/h)c时出现滑行水流流态。

3.2 计算过程

将台阶看成糙体，其糙度用k*=hcosα表示，摩擦系数f用参数F*表示,其公式为

(3)

式中:q为单宽流量；g为重力加速度；α为泄槽坡度。

滑掠水流里初始掺气点的位置在距堰顶长度为L1处，则

L1=k*9.719(sinα)0.079 6F*0.713。

(4)

渐缩式泄槽对初始掺气点的位置也会有影响，会使之提前，渐缩式泄槽初始掺气点的位置在距堰顶长度为L1′处，其计算公式为

(5)

式中b1和b2分别为泄槽初和泄槽末的断面宽度(m)。

该断面中心水深d1为

(6)

则该断面两侧边墙处的水深高于中心处的水深，计算公式为

(7)

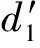
由文献[11]、文献[21]介绍，在初始掺气点后不远处，台阶式溢洪道开始均匀掺气。均匀掺气点的公式还在探索阶段。均匀掺气水流的水深d0计算公式为

(8)

其中，

fe=0.5(1+thx) 。

(9)

式中thx为双曲线正切函数，其中：

(10)

Ce=0.9sinα。

(11)

4 工程实例

某水库溢洪道闸室段后有溢洪泄槽陡坡，溢流堰堰顶高程为46.19 m，桩号0+004.40 m为泄槽初始断面，高程为44.20 m，前接溢流堰，后接高为0.6 m、长为3.0 m的第一级台阶；随后接高为0.6 m、长为3.0 m的台阶到桩号0+076.40 m；再之后为消力池；桩号0+094.40 m为溢洪道终点。溢流堰段、泄槽终点段如图2所示。溢流堰净宽为67.0 m，泄槽从桩号0+004.40 m收缩到桩号0+076.40 m，之后净宽为27.0 m，为渐缩式泄槽。已知水位在49.27 m高程时，溢流堰下泄单宽流量为11.61 m2/s，按照起始断面水深计算公式[14]得到桩号0+004.40 m处泄槽中心水深为1.45 m。边墙处的计算水深也在中心处水深的基础上作上述变换。

图2 泄槽首尾剖面图Fig.2 Cutaway drawing of chute

4.1 模型试验简介

试验目的：由于溢洪道及消力池的水力学条件比较复杂，特开展相应水工模型试验研究，复核溢洪道在各种频率下的泄流能力，通过研究分析，确定最优除险加固方案。

试验设计：模型比尺为1∶20，相应的流速比尺为1∶4.472 1；流量比尺为1∶1 788.854 4。泄槽混凝土糙率为0.014，模型中的泄槽糙率应为0.008 5，选取灰塑料板和有机玻璃作为模型中泄槽的制模材料。模型中上游水库高约2.5 m，能够保证溢洪道进口水流平稳。下游河道地形用水泥砂浆抹制。

模拟范围：纵向长390.50 m，其中下游河道长182.00 m；横向宽99.0 m，垂向高程范围为5.0～51.2 m(因动床冲刷试验需要预留冲刷坑深度，下游底高程按5.0 m考虑)。

本文主要观察了光滑溢洪道和不同水位下台阶式溢洪道内的水流状态，并选取某一水位下，根据测针测得泄槽内各桩号处断面的水深，与本文提出的改进系数法计算出的泄槽水深比较分析。

4.2 试验与计算结果对比

光滑溢洪道泄槽内的水流如图3所示，泄槽尾部出现水冠，威胁建筑物安全；台阶式溢洪道不同水位下泄见图4，台阶式溢洪道棱形波减弱，两侧边墙壅水减小，可见台阶式溢洪道消能效果显著。

图3 光滑溢洪道水流流态Fig.3 Flow pattern in smooth spillway图4 台阶式溢洪道流态Fig.4 Flow patterns in stepped spillway

试验针对设计洪水位下台阶式溢洪道的下泄情况，在对应于实际工程桩号0+004.40，0+034.40，0+046.40，0+076.40 m处布置测点，进行比较分析。模型试验观测的水深经过换算后和计算出来的水深比较见表1。

表1边墙水深计算值与试验值对比
Table1Comparisonofsidewallwaterdepthbetweencalculatedvaluesandtestvalues

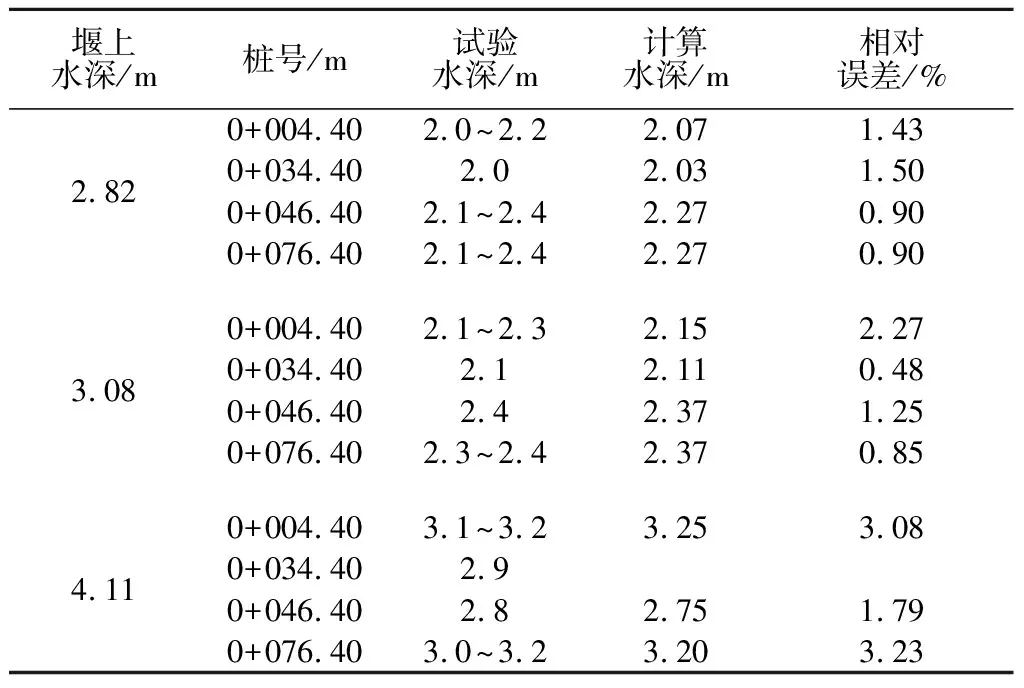
堰上水深/m桩号/m试验水深/m计算水深/m相对误差/%2.823.084.110+004.402.0～2.22.071.430+034.402.02.031.500+046.402.1～2.42.270.900+076.402.1～2.42.270.900+004.402.1～2.32.152.270+034.402.12.110.480+046.402.42.371.250+076.402.3～2.42.370.850+004.403.1～3.23.253.080+034.402.90+046.402.82.751.790+076.403.0～3.23.203.23

注：当库水位为50.30 m，堰上水深为4.11 m时，泄流在0+046.40 m桩号左右开始掺气，所以在0+034.40 m桩号无计算水深

通过比较可以发现，桩号为0+004.40 m处为泄槽起始处，该断面水深参照规范计算得到，由于此断面两侧边墙已经开始渐缩状态，中心水深与两侧边墙水深也满足折减关系，可以作为本文改进系数法的参照。当库水位为49.01 m和49.27 m时，下泄水流在0+034.40 m桩号左右开始表面掺气，该断面实测水深与计算水深的相对误差最大为1.50%。水深经过短暂的过渡后，下泄水流水深在一个稳定的范围内波动。综合文献[21]的无因次图表和此次模型试验的观察，桩号0+046.40 m为2种计算水位(49.01 m和49.27 m)下均匀掺气位置，之后实测水深与计算水深的相对误差最大为1.25%。桩号0+076.40 m处泄槽断面宽度为27.00 m，之后为消力池，此断面实测水深与计算水深的相对误差最大为0.90%。当库水位为50.30 m时，下泄水流在0+046.40 m桩号左右开始表面掺气，该断面实测水深与计算水深的相对误差为1.79%。经过过渡之后，后续一直为均匀掺气，水深稳定不变，均匀掺气时的实测水深与计算水深的误差可用桩号为0+076.4 m处的相对误差表示，为3.23%。从表1中可以看出，改进系数法对渐缩式台阶溢洪道两侧边墙处的水深计算相对误差不超过5%，拟合度好；其次本文在3个水位下进行比较，随着水位升高，单宽流量增大，误差也在增大，与台阶式溢洪道计算方法适用于小单宽流量吻合。

5 结 语

本文从工程实例出发，在原有昌桑法的基础上，提出了改进系数法，用以计算渐缩式台阶溢洪道两侧边墙处的水深，以此为依据设置边墙高度，在高效消能的情况下，保护泄水建筑物的安全。台阶式溢洪道消能效果和掺气效果显著，适合应用于各种复杂地形地质条件，通过研究发现，本文提出的方法计算简便，精度高，对后续的台阶式溢洪道水力特性研究具有重要的参考价值，为工程应用提供了科学理论依据。