基于网格搜索优化的主成分分析-支持向量机算法的冷水机组能耗预测

2019-03-19黄真银徐成良陈焕新李昱瑾

制冷技术 2019年6期

刘峥，黄真银，徐成良，陈焕新*，李昱瑾

（1-华中科技大学中欧清洁与再生能源学院，湖北武汉 430074；2-湖北卓立集控智能技术有限公司，湖北宜昌 443000；3-华中科技大学能源与动力工程学院，湖北武汉 430074）

0 引言

随着新时期下城镇化及工业化进行的飞速推进，我国能源需求不断增加，节能减排工作也日益紧迫。高能耗设备因其在用数繁多、点多面广、耗能大和能源使用效率低等特点，具有巨大的节能潜力[1]。因此，对高能耗设备的能耗分析和节能改进尤为重要[2-6]。

近年来，基于数据挖掘的建筑能耗数据分析相关研究正在越来越广泛[7-8]。WANG 等[9]基于建筑能耗数据开发了一个集成工具包原型，并进行了验证，该方法能够有效地检测运行不良和能源浪费。侯博文等[10]采用网格搜索法优化的支持向量机模型用于建筑能耗预测，优化结果显著，能很好地完成建筑能耗预测工作。丁飞鸿等[11]采用遗传算法优化决策树模型用于短期建筑能耗预测，与传统的回归模型相比，该模型预测精度有明显提高。邓晓红等[12]利用粒子群算法优化最小二乘支持向量机（Particle Swarm Optimization of the Least Squares Support Vector Machine，PSO-LS-SVMR）模型用于公共建筑短期能耗预测，并将预测结果与递归神经网络（Leven-Berg-Marquardt Back Propagation Neuron Network，LBM-BPNN）模型作对比，结果表明PSO-LS-SVMR模型具有更好的预测精度。

除了用于建筑的能耗分析，数据挖掘在空调领域的能耗研究也正在成为一项重要的课题[13-15]。XIAO等[16]通过关联规则算法分析建筑中空调设备能耗数据的问题，有效降低了能耗。YU等[17]利用数据挖掘技术中的关联算法分析了耗能体的年能耗数据和日能耗数据，通过对空调系统运行能耗数据的异常识别，找出了空调设备运行过程中的能源浪费及设备故障问题，挖掘了节能潜力，证明了该方法的有效性。廖文强等[18]利用长短期记忆神经网络（Long Short-Term Memory，LSTM）对空调系统进行能耗预测，与传统的预测方法相比具有更好的精度。王智锐等[19]分别用支持向量机（Support Vector Machine，SVM）模型和自回归滑动平均（Autoregressive Moving Average，ARMA）模型对夏季空调负荷进行预测，结果表明SVM模型具有更好的精度和泛化能力。

本文利用 10折交叉验证和网格搜索法优化的支持向量机模型对冷水机组的能耗进行预测，在获得输入数据阶段，引入了主成分分析（Principal Component Analysis，PCA）数据简化方法，观察PCA对支持向量机模型的影响。在模型评价阶段，本文采用了平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、拟合优度（R2）三个评价指标。

1 网格搜索法优化PCA-SVM

网格搜索法是支持向量机可调参数寻优的一种方法，主成分分析（PCA）的目的是获得变量降维的简化计算，将两者与支持向量机（SVM）结合得到网格搜索法优化PCA-SVM模型。

1.1 PCA数据简化法

在能耗预测模型建立过程中，若存在多个与能耗具有相关性的变量，这些变量全部参与建模，无疑增大了建模问题的复杂程度，进而增加建模成本，PCA是一种对数据进行降维并找到更少的彼此线性不相关的变量来代替原有变量的数据简化方法[20]。判断是否利用 PCA进行降维主要通过相关性分析，若存在两个变量之间的相关性达到0.7及以上，需利用PCA进行降维。

分析不同属性数据之间线性相关程度的强弱，并用适当的统计指标表示出来的过程称为相关性分析[21]。本文在进行相关性分析时所采用的指标为Pearson相关系数（r），其计算如式（1）所示：

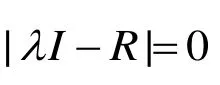
1.2 支持向量机（SVM）

SVM是基于统计学的一种监督式学习方法，普遍应用于数据分类和回归分析。

SVM用于回归分析的基本思路为：对于n个输入变量和m组数据的训练样本，即T={(x11, y1),…(xij,yj),…(xmm, ym)}。设支持向量回归的超平面的拟合函数为y=b+WTX，W为权重系数向量，b为偏置量。利用拟合函数所得的预测值和实际值之间有一定的差值，若差值大于 ε，则对损失函数有贡献，若小于ε，则无贡献。

损失函数为：

1.3 支持向量机（SVM）参数寻优

在使用SVM算法建模时，存在惩罚参数C、核函数参数g等可调参数会对建模结果产生较大影响。其中惩罚参数C影响模型的拟合程度，而核函数参数g影响支持向量的个数。确定最佳的C、g参数在SVM算法建模中显得尤为重要，本文通过交叉验证法与网格搜索法对C、g参数进行寻优，以实现对SVM的优化。

N折交叉验证法的基本原理：轮流N次将数据集划分为大小一致的N部分，用其中的N-1部分作为训练集，剩余的1部分作为验证集，N次验证结果的精度的平均值作为对建模精度的估计值。

网格搜索法优化SVM模型参数的基本思路：1）利用网格搜索法找出用于建模的所有可调参数并进行参数组合；2）依次对所有参数组合进行支持向量机建模；3）以N折交叉验证法下的建模精度为判断依据得出最佳模型和可调参数。

1.4 网格搜索优化PCA-SVM算法流程

图1所示为PCA-SVM算法流程，整个流程分为4个部分。

1）数据预处理：对原始数据集进行冗余属性剔除，缺失值及异常值处理，数据规范化处理等工作；

2）主成分分析：利用相关性分析计算各个变量之间的相关系数，利用主成分分析构建新变量；

3）构建模型：将得到新变量的数据按照4:1的比例构建训练数据和测试数据，利用训练数据训练出支持向量机模型；

4）优化模型：利用10折交叉验证和网格搜索法得到最优的惩罚参数C、核函数参数g的取值，同时得到最优的支持向量机模型。

图1 PCA-SVM算法流程

2 基于PAC-SVM离心式水冷机组能耗预测模型

2.1 空调水系统工作原理图及数据来源

本文以某医院的离心式冷水机组为研究对象。该医院总建筑面积为37,000 m2，地上5层，地下2层。建筑包含病房、包间、贵宾室、会议室和大堂等多种不同类型的空间，所有空间的夏季冷负荷为1,797 kW，冬季热负荷为1,677 kW。建筑的供冷需求时段在6月至10月，供暖需求时段为11月至第二年的4月。

图2所示为该建筑的空调水系统工作原理，整个系统以两台离心式冷水机组作为冷源。在冷冻水部分，采用复式泵系统，冷源侧一台泵对应一台冷水机组，泵的扬程用于克服冷水机组中换热器的阻力；负荷侧3台泵并联，泵的扬程用于克服空调末端换热器和管路中各个部件的阻力，负荷侧的循环泵流量随负荷变化而变化。在冷却水部分，采用“一泵对一机”的方式，当一台冷水机组关闭时冷却水循环泵随之关闭。

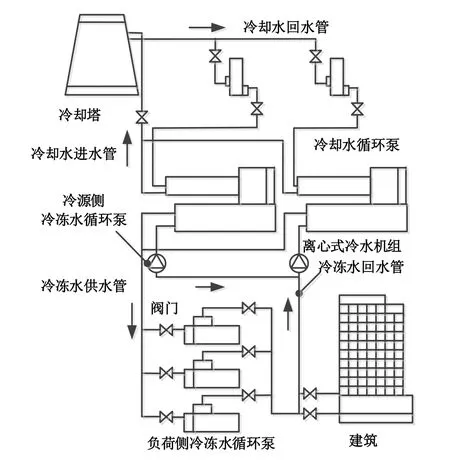
图2 空调水系统工作原理

采集课题研究所用的数据时，在系统的各个关键位置布置传感器，利用中央空调机房群控与楼控装置对数据进行记录和储存，频率为1次/min，记录对象包括室外温度、湿度以及分布在室内的各类传感器采集的数据。本文选择装置存储的 2017-09-04—2017-10-04一整月的数据为源数据，以其中冷水机组的瞬时功率作为预测对象，剩余的因素作为可能影响冷水机组能耗的对象展开研究。

2.2 数据预处理

离心式冷水机组作为高能耗设备，其能耗数据具有非线性、多因素、时变复杂、高重叠与强噪音等特点[20]，需通过数据预处理得到对建立模型有意义的数据。本文依次对原始数据进行了缺失值及异常值处理，冗余属性剔除和数据规范化等处理，其中缺失值处理采用回归补插法，数据规范化处理采用最小-最大规范化法，最终确定冷冻水进水温度、蒸发温度和瞬时功率等16个变量以及24,953组时序数据用于建立能耗预测模型。

2.3 PCA数据简化

对变量进行相关性分析，计算除瞬时功率外其他 15个变量两两之间的相关系数，相关系数绝对值分布如图3所示。

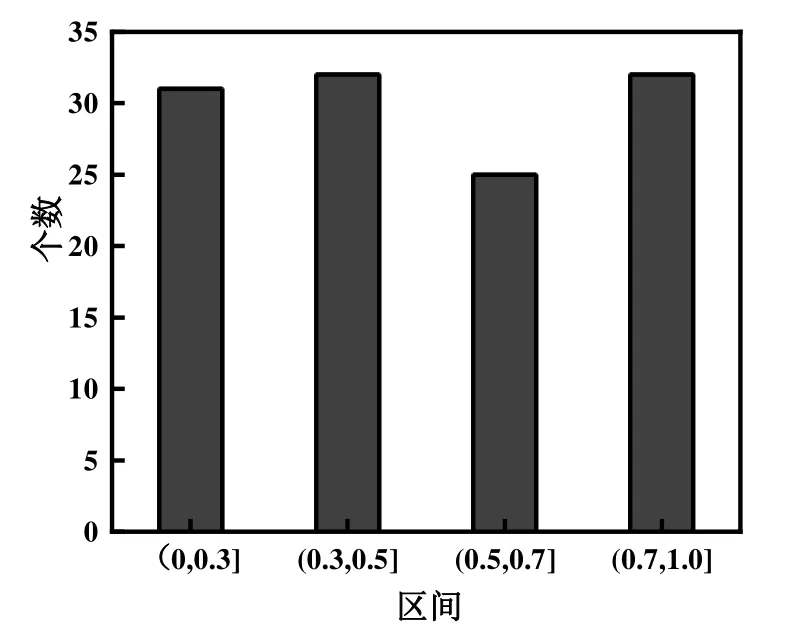
图3 相关系数绝对值分布

图3中总共120个相关系数，绝对值落在(0, 0.3]区间的数量为31，绝对值落在(0.3, 0.5]区间的数量为32，绝对值落在(0.5, 0.7]区间的数量为25，绝对值落在(0.7, 1]区间的数量为32。即存在多组变量之间的相关性达到0.7及以上，需要利用主成分分析进行降维，主成分分析结果如表1所示。

表1 主成分分析

由表1可知，前4个新主成分累计方差比率达到92.43%，可选取这4个变量作为新的建模变量，将输入数据从15个变量的维度减少至4个变量的维度。

2.4 模型建立及参数寻优

本课题分别对训练数据建立 SVM-A、SVM-B和PCA-SVM-B预测模型。SVM-A模型直接将影响冷水机组瞬时功率的 15个变量作为模型的输入，利用支持向量机回归模型进行预测。SVM-B模型在SVM-A模型的基础上进行可调参数寻优，利用优化后的模型进行预测。PCA-SVM-B模型对上述15个变量进行主成分分析，将构建的4个新变量作为模型的输入，参数寻优之后利用优化后的模型进行预测。

进行网格搜索时，利用2的指数穷举参数取值，SVM-B模型和PCA-SVM-B模型可调参数C的取值范围为(2-2, 210)、g的取值范围为(2-5, 25)，参数的所有组合种类为143种。参数寻优时，采用10折交叉验证算法对模型进行精度评估。

在对支持向量机算法进行可调参数寻优时，往往存在多组参数组合的模型精度相近的情况，为了避免大C值造成模型过拟合、泛化能力差，此时参数值应尽量选取C值较小的参数组合。本课题SVM-B模型中C=16、g=0.125，PCA-SVM-B模型中C=16、g=1。

3 模型预测结果与分析

SVM-A模型的能耗预测结果如图 4所示，粗实线代表预测值与实际值完全吻合，细实线之间区域为 90%的置信度空间。进一步分析，SVM 模型预测值与实际值之间的平均绝对误差（MAE）为0.023，均方根误差（RMSE）为 0.059，拟合优度（R2）为0.877，建模时长为0.15 min。

图4 SVM-A模型的能耗预测结果

SVM-B模型的能耗预测结果如图5所示，将图5和图4作对比，发现优化后的模型SVM-B较模型SVM-A的预测精度有较大提升。

PCA-SVM-B模型的能耗预测结果如图6所示，将图6和图5作对比，发现采用PCA-SVM-B模型预测精度较SVM-B模型预测精度有略微降低。

表2所示为模型评价指标的对比。由表2可知，SVM-B模型较SVM-A模型在MAE、RMSE和R2这3个指标上都有较大的提升，其中MAE减小了43.48%，RMSE减小了71.19%，R2增加了12.88%，但是建模时长增加了近130倍。而PCA-SVM-B模型较SVM-B模型在MAE、RMSE和R2这3个指标上数值相近，但是建模时长缩短了80%。