金属软管失稳分析及结构优化

朱金花，牛铮，危书涛，范海俊，李永泰，董卫华

（1.合肥通用机械研究院有限公司；2.国家压力容器与管道安全工程技术研究中心，安徽 合肥 230031；3.中国石化镇海炼化分公司，浙江 宁波 315207）

金属软管是一种重要连接构件，具有柔性大和装卸简单的优点，目前被广泛应用于现代工业管路系统中；主要作用是降低管路振动的传导、补偿两端连接管道的热变形及沉降差。金属软管结构复杂，主要由波纹管、金属编织网套和接头三部分组成，波纹管是主体，主要起密封作用；网套起加强和屏蔽的作用；接头将网套与波纹管连接为一体，是金属软管之间、金属软管与其他设备和管件、连接的部件，其结构形式主要是成品法兰，为刚性元件。

近年来随着金属软管的普及，其失效案例日益增多。研究表明金属软管的主要失效形式为波纹管腐蚀泄漏、钢丝网套脱落及钢丝断裂、接头焊缝开裂及腐蚀泄漏等，研究人员亦根据上述失效形式对应的失效模式和机理提出相应的预防措施。但调查发现金属软管的失效不仅仅包含以上形式，用作补偿地基沉降差的大量金属软管在使用一段时间后表面变形严重（图1），网套鼓包，局部与波纹管分离，已成为管路或设备系统的安全隐患，因此对该部分金属软管的失效模式及失效原因开展研究，提出相应的解决方案尤为必要。

图1 金属软管变形形貌

1 金属软管概况

图1为安装在某油罐根部进出油管阀门前的金属软管，主要用途是补偿管路系统和油罐的沉降差。照片显示该金属软管网套已发生失稳失效，失效形貌为两端鼓包位置波纹管与网套分离，宏观检查未发现网套钢丝有断裂现象。表1为该金属软管的主要参数。

表1 金属软管主要参数

2 失效分析

参照标准GB/T30579-2014《承压设备损伤模式识别》，初步判断金属软管的失效模式为过载引起的失稳。拆卸后对金属软管解剖后发现内部波纹管平面失稳，其失稳形貌为波峰半径增大，波谷半径减小，两边侧壁互相靠拢。对金属软管的工作工况调查确认该金属软管两端的管路系统和油罐的沉降差已达30mm，该沉降差形成的附加横向位移可能是金属软管发生失稳的主要原因。

3 失稳计算

采用有限元方法对金属软管进行分析时，不考虑端部法兰结构对波纹管及网套的影响，仅考虑直管、波纹管与网套三部分。

3.1 技术参数

波纹管、直管及网套钢丝材质均为0Cr18Ni9，计算时本构关系为理想弹塑性模型，屈服强度205MPa，弹性模量195GPa，泊松比0.3。金属软管的主要几何参数见表2。

表2 金属软管主要几何参数

图2 波纹管剖面图

3.2 计算模型

图3 金属软管有限元计算模型图

图4 横向位移作用下一阶失稳模态

有限元计算时采用参数化建模，直管和波纹管壁厚较小，可考虑为薄板结构，网格选用板壳单元shell181，网套选用梁单元beam189。网套与直管段、网套和波纹管之间设置接触对，接触类型为standard，摩擦系数为0.2；直管段与网套端部节点之间同样设置接触对，接触类型为bonded（always）。有限元计算模型及划分后的网格如图3。金属软管法兰刚度远大于网套、波纹管及直管段刚度，因此有限元模型一端端面施加全约束，另一端端面根据计算要求设置不同的边界条件。

3.3 失稳计算

有限元计算采用屈曲分析方法，图4为该金属软管在横向位移作用下的一阶失稳模态，临界失稳载荷为217mm。失稳模态为网套两端鼓凸，一侧与波纹管分离，与图1所示的失稳形貌吻合。

图5为金属软管内压作用下的一阶失稳模态，对应的失稳载荷为0.35MPa。失稳形貌为波纹管波峰外凸半径变大，波谷弧度减小、两侧壁靠拢，和图2中波纹管剖面图变形趋势一致。

有限元计算分析表明该金属软管的失效模式为过载引起的失稳，其中网套失稳原因为管路系统和罐底基础的沉降差引起的附加横向位移，波纹管失稳原因为内压引起的平面失稳。

4 结构优化分析

图5 内压作用下一阶失稳模态

金属软管在横向位移作用下发生失稳，网套与波纹管分离，失去网套的支撑保护，金属软管的承载能力急剧下降，运行风险大大增加。标准SH3412-2017《石油化工管道用金属软管选用、检验及验收》中规定了不同用途的金属软管的长度选择要求，但对长径比小的金属软管在安装时无法预留合适的长度，后期安装后沉降差形成的附加横向位移无法避免，因此应对金属软管的局部结构进行优化，提高其承载能力。下文对波纹管和网套的几何参数影响进行了相关分析，为结构优化提供指导。

4.1 波纹管几何参数影响

波高和壁厚是波纹管的重要参数，其数值不仅影响金属软管在位移作用下的稳定载荷，同时影响内压作用下的稳定载荷。

表3列出了不用波高对应的横向位移和内压作用下的金属软管失稳载荷，图6为变化趋势曲线。结果表明随波高增加，横向位移作用下的失稳载荷呈线性增大趋势，但内压作用下的失稳载荷呈线性下降趋势。因此波纹管波高增加，金属软管的横向位移补偿能力提升，但内压稳定性下降。当管路系统设计压力较低且位移补偿量较大时应采用增大金属软管波纹管波高的方法提高其稳定性，保障金属软管安全运行。

表3 不同波高对应的失稳载荷

图6 失稳载荷随波纹管波高的变化曲线

表4列出了不同波纹管壁厚对应的横向位移和内压作用下的金属软管失稳载荷，图7为变化趋势曲线。结果表明随壁厚增加，横向失稳位移和内压作用下的失稳载荷均呈线性增加趋势。因此波纹管壁厚增加，金属软管位移和内压作用下的稳定性均得到提高。当管路系统设计压力较高且位移补偿量较大时应采用增加金属软管波纹管壁厚的方式提高其承载能力，保障金属软管安全运行。

4.2 网套几何参数影响

网套编织角和钢丝股数是网套最重要的工艺参数，主要影响金属软管在位移作用下的失稳载荷。

表4 不同波厚对应的失稳载荷

图7 失稳载荷随波纹管壁厚的变化曲线

表5列出了不同编织角对应的横向和内压作用下的金属软管失稳载荷，图8为变化趋势曲线。结果表明编织角在40°～50°时，横向和轴向压缩位移作用下的失稳载荷基本保持不变，当编织角继续增大，数值迅速减小；内压作用下的失稳载荷一直保持不变，数值为0.35MPa。因此金属软管的网套编织角参数不可过大，应小于50°。研究了内压、轴向拉压及弯曲载荷单独和联合作用下的最佳编织角，指出内压作用下的网套编织角应小于50°40’，轴向位移作用下的网套编织角应为35°～50°间，为保证金属软管的柔性和稳定性，推荐金属软管的最佳编织角为40°～50°之间。

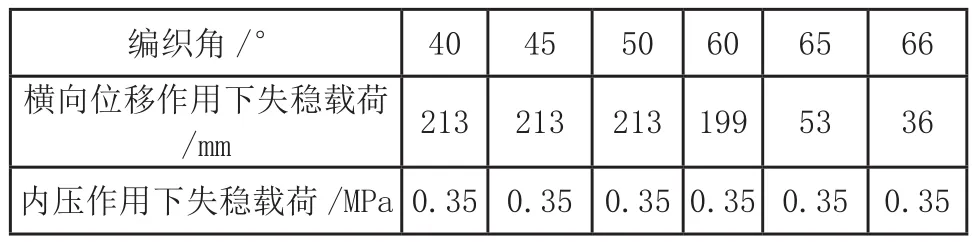
表5 不同编织角对应的失稳载荷

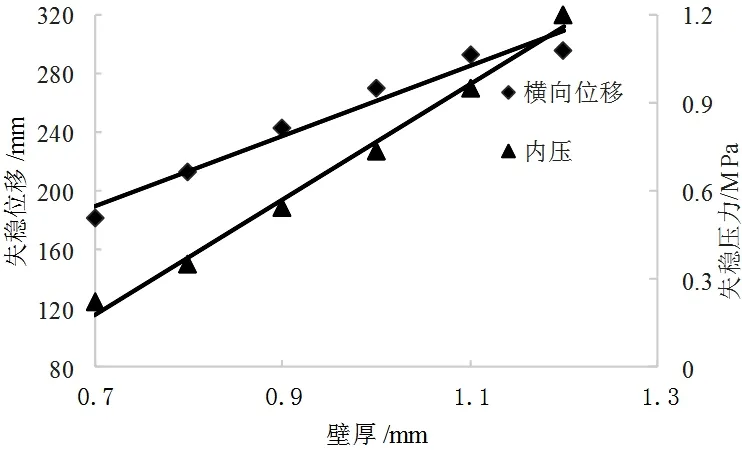
图8 失稳载荷随网套编织角的变化曲线

表6给出了不同钢丝股数对应的横向位移和内压作用下的金属软管失稳载荷，图9绘制了变化趋势曲线。结果表明当网套钢丝股数从136股增大到296股，横向位移和内压作用下的失稳载荷保持不变，其承载能力未得到有效提高。韩淑洁等研究亦表明网套钢丝股数增加对金属软管的弯曲刚度影响较小，且伴随着金属软管柔性性能下降，因此不建议采用增加钢丝股数的方法来提高其稳定性。

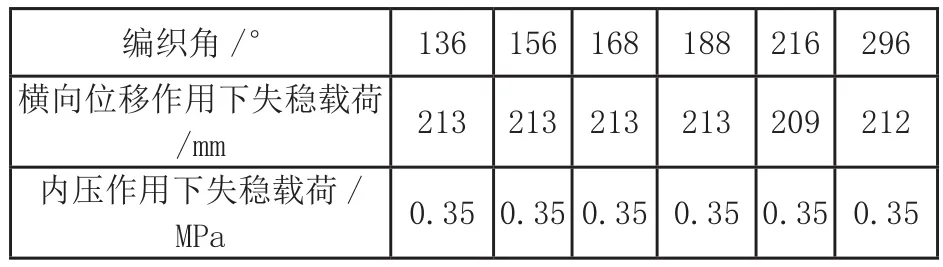
表6 不同钢丝股数对应的横向失稳载荷和轴向载荷

图9 失稳载荷随网套钢丝股数的变化曲线

5 结语

金属软管的网套失稳为横向位移作用，波纹管失稳为内压作用；失稳时网套与波纹管分离，金属软管承载能力将大大下降，影响金属软管甚至管路系统的安全运行，应予以重视。对长度较长的金属软管可采用相关标准选择合适的长度避免失稳发生，对长径比小的金属软管可通过优化局部结构提高其稳定性。金属软管的结构优化应根据其使用条件选择不同的优化方法，具体建议如下：（1）沉降差大、设计压力低的管路系统的金属软管应适当增大内部波纹管波高；沉降差大、设计压力高的管路系统的金属软管应适当增大内部波纹管壁厚。（2）金属软管的最佳编织角在40°～50°之间；钢丝股数增加不能提高金属软管在横向位移和内压作用下的稳定性。