不等式证明的方法研究
2019-03-19黑龙江省哈尔滨市工业大学附属中学校张天慧
黑龙江省哈尔滨市工业大学附属中学校 张天慧
不等式是高中数学教学内容中的一个重要组成部分,是研究其他数学问题的重要工具。不等式的证明方法有很多,涉及高中数学体系的方方面面。调查表明,学生在进行证明时往往无法快速地选择出最合适、最简便的方法,因此,教师如何将证明不等式的方法有效地渗透给学生,成为高中数学教学的一个重难点。
一、研究不等式证明的教学意义分析
首先,不等式是高中数学知识体系中一种广泛被使用的辅助工具,在其他很多数学问题的分析与解答中都需要使用到不等式的知识,但是在使用不等式的过程中,很多时候需要我们先证明不等式的可行性。因此,研究不等式的证明方法是教学的切实需求,是学生学习数学知识的必经之途。
其次,在不等式证明教学中可以有效地锻炼学生的逻辑思维能力。不等式证明的方法非常多,在高中数学中只涉及了一些关键的研究方法。在这些方法的教学中,渗透着经典数学思想的精髓,通过记忆与推理的紧密结合,可以有效地达到锻炼学生逻辑思维的目的。
最后,通过严谨的不等式证明方法的学习,可以帮助学生养成严谨思考的习惯,培养学生良好的学习精神和习惯,这种行为习惯的形成对学生综合素养的提升具有重要的帮助,对学生其他科目的学习也有很大的帮助。
二、两种不等式证明的方法教学探讨
在高中阶段需要学习的不等式的证明方法有很多,主要用到的有放缩法、柯西不等式、比较法、反证法、换元法等。下面,我将针对放缩法和柯西不等式两种主要的方法进行教学讲解。
1.放缩法
放缩法是指要证明某个不等式如A<B,可以首先将不等式的一边进行放大或者缩小,寻找一个中间量,如将A放大成为C,如果我们可以首先证明C<B,那么比C还要小的A自然也要小于B,即A<C<B,实际上是使用了不等式的传递性,而这种间接证明的方法就被称之为放缩法。放缩法是研究不等式证明方法里常见的一种方法,它是通过思想转换来实现证明的,对学生思维具有很重要的启发作用,在教学过程中应当得到教师的足够重视,帮助学生对放缩法的使用做到熟能生巧。放缩法的含义非常简单,在教学中最重要的是培养学生的使用意识,当面对此类题型时,学生可以一眼看穿,直接使用放缩法进行迅速证明。下面我们用一个经典例题来看看放缩法的具体使用过程。
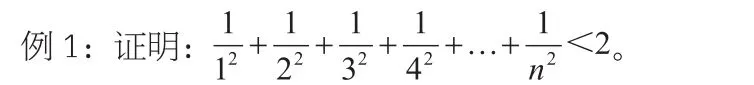
分析:这是一个基本又经典的利用放缩法来证明不等式的题目,在解答这个题目时,我们可以看到这个题目属于A<B的类型,于是我们可以首先将不等式左边的A进行放大,可以首先得出:可以看出在这个不等式中的右边是我们非常熟悉的一个式子,可以通过裂项来计算,得出不等式右边等于2-<2,于是证明了原不等式。
使用放缩法进行不等式的证明时,有一些有效的技巧可以让学生记住:遇见分式可以尝试放大或者缩小分子或者分母;构造出等比数列进行放缩;利用裂项求式来进行计算放缩;利用错位相减来进行放缩等。教师需要在教学中积极总结题型经验,把握命题规律,提升学生快速解决不等式证明问题的能力。
2.柯西不等式
柯西不等式同样是不等式证明中的一个重要方法,柯西不等式具有多种形态,我们通过柯西不等式的一般形态进行讲解。柯西不等式的一般形态为(a2+b2)+(c2+d2)≥(ac+bd)2,在实际使用过程中,我们经常会对这个公式进行变形,因此,一般还会用到ac+bd≤,等号成立的条件是有且仅有ad=bc,这个公式就代表柯西不等式。除了上面的一般形式,柯西不等式还存在向量形式、三角形式、概率论形式、积分形式等多种表现形式,也因此在教学中有着广泛的应用。下面,我们通过一个简单的例题来具体探讨柯西不等式在不等式证明方面的应用途径。
例2:已知三个正数a,b,c互不相等,证明:
分析:这个不等式刚看上去很难掌握其中的关键,因此我们首先可以通过变形来获得其中的关键。由于三个分母都是正数,所以我们可以首先将不等式右边的分母移到左边来,可以获得:对这个式子通过一系列的化简,可以得到该式子≥=(1+1+1)2=9,又由于三个字母互不相等,所以需要注意等号是取不到的。
使用柯西不等式来证明不等式时的技巧一般是通过拆常数、凑常值来进行的。柯西不等式是不等式证明方法中一个常用但是困难的方法,需要教师为学生多总结解题经验,找到其中的规律,最重要的是要让学生多做题,自己找出其中的规律,对这几种常见的题型做到烂熟于心,从而迅速地解决问题。
除了放缩法和柯西不等式法之外,在高中数学教学中涉及的不等式证明方法还有很多,需要教师为学生进行一一细致讲解,可以通过一些经典例题的讲解帮助学生真正地理清其中的区别与联系,使学生在解题时能够迅速地找出解决问题的最适合方法,并提升学生的解题能力,培养数学核心素养。
