基于销售奖励契约下的多随从双层条件风险值决策模型
2019-03-19,,
,,
(1.浙江工业大学 经济学院,浙江 杭州 310023;2.浙江工业大学 管理学院,浙江 杭州 310023)
多随从风险决策问题在供应链中普遍存在,如一个供应商向多个零售商进行产品批发与销售问题,供应商决定供应量和批发价,零售商决定订购量,多随从风险决策问题可以用一个双层优化模型刻画与解决。因此,研究供应链多随从问题的双层规划模型的建立与求解具有重要的理论意义和实际价值。自1952年Stackelberg提出了双层决策模型(也称为双层规划)以来,单从属双层规划的理论与应用研究取得了相当丰富的研究成果[1-4],多随从双层决策模型(或称多随从规划、多随从双层规划、多随从决策模型)也已经有了一定的研究成果,主要包括理论、算法和应用等3个方面:1) 研究多随从决策模型的最优解的定义及性质,其研究内容包括最优解的存在性、模型转化为另一容易求解形式的等价性证明和最优解的条件等性质[5-10];2) 研究多随从决策模型的求解算法,大多研究都集中在线性多随从规划的求解算法[11-23];3) 研究实际问题中的多随从决策模型,一般都是根据实际问题来建立特殊的多随从决策模型,在供应链、电力供应和电信等领域中应用[24-33]。特别是在供应链契约方面,也有部分学者进行了研究[34],如刘玉霜等[35]讨论了两级供应链含一个制造商与两个随从零售商的最优协调问题。赵泉午等[36]研究了在单个供应商和多个零售商构成的易逝品两级供应链中,建立一个博弈模型,证明了各零售商之间存在NASH均衡。李绩才等[37]以一个两阶段的供应链系统为研究背景,建立了下游损失厌恶型零售商之间存在竞争的收益共享契约协调模型。李占雷等[38]运用前景理论中损失厌恶概念,研究了零售商在损失厌恶下的供应链回购契约模型。张春伟等[39]研究了零售商具有多个零售点时的回购契约模型。张寒[40]建立了石油分销系统中单分销商多个零售商的多随从Stackelberg博弈模型。洪璐等[41]研究了CVaR准则下考虑后续服务产品的多随从收益共享契约模型。以上研究,他们均采用两级博弈模型,目标均为利润最大化,没有考虑风险损失。国外关于契约的研究非常多,如Güray等[42]基于批发价合约、回购合约、收益共享合约和数量折扣合约等,研究了带随机收益和随机需求的供应链的协同问题。Choi等[43]研究一个批发价格契约模型的供应链协调问题。
综上所述,多随从双层决策模型理论研究并不多,算法研究也仅集中在线性情况,应用模型在供应链契约中的研究也不多,均用期望均值考虑风险目标。目前,多随从决策模型的算法基本是针对线性模型提出的,求解多随从非线性双层决策模型的主要思路是通过转化成均衡约束研究简化求解的难度,如利用KKT条件转化成互补约束问题求解,将提出一种销售奖励契约的多随从双层风险决策模型,提出一种近似求解方法。
1 奖励供应链风险相关研究及条件风险值
供应链契约主要包括批发价折扣契约、数量柔性契约和回购契约等,其中销售奖励契约是数量柔性契约一种,销售奖励契约是指零售商向供应商订购一定数量的产品,根据零售商销售的数量,供应商给出相应的利润奖励,这样有利于零售商订购更多的商品进行销售,使得双方获得更多的利润,同时降低零售商损失风险。现有的销售奖励契约研究文献并不多。Wang等[44]研究了由一位供应商和多位零售商构成的供应链奖励契约(多随从契约情形),建立了一个基于各方基础存货水平的竞争水平下的博弈模型,发现竞争会在所有的零售商间及与供应商之间展开。Christoph等[45]给出了一种如何设计奖励契约来协调供应链内的决策,表明了如果与经营层面互动那么可以产生大量的契约收益。Adolfo等[46]研究了三种形式的供应商数量激励契约以得到不同程度的安全性和弹性,包括了在途库存和仓储库存以体现需求可变性。Kremer等[47]研究了一种数量契约模型,基于数值研究按照模型来设计最优的契约订购量。Youssef等[48]研究了OEM厂商将某些生产行为外包给承包制造商的奖励契约问题,结果表明多决策层次的下订单战略比只有一个决策层次的下订单战略表现更好。Xiong等[49]将回购契约和数量柔性契约结合在一起引入一个组合契约(CP),证明了该CP合约在供应链协同、利润分配和风险分配方面比单种契约有优势,在风险分配方面也比成分合约更具弹性。
Sun等[50]研究了一些典型合约的激励机制在缓解供应链成员间破产宣传的效果,包括收益共享契约、价格折扣契约及数量柔性契约。刘彦利[51]系统地研究基于绩效奖励的易逝品供应链联合契约问题,建立了由一个制造商和一个零售商构成的易逝品两阶层供应链模型,在分析绩效奖励机制对此供应链协调效果的基础上,建立了相应的销售奖励契约模型。甘骞等[52]研究了基于销售奖励与回购契约的供应链协调机制,提出了一种销售奖励契约模型,导出了在回购契约下最优订货量和回购价格的解析形式。李凯等[53]研究了基于奖励与惩罚的双重契约的供应链渠道协调问题,设置奖惩额度和比例作为协调因子,建立了一个惩罚和奖励相结合的供应链契约模型。郭飞等[54]运用CVaR准则建立了的一个供应商与一个零售商的供应链销售奖励的双层风险决策模型。
研究表明:奖励契约可以有效地调节供应链协调,使得供应链双方获得更多的利润。但是,对闭环供应链以及渠道供应链奖励的研究并不多[55-56],而且针对已有的销售奖励契约对下层考虑风险损失的研究并不多,运用条件风险值测度也很少[57],因此将运用条件风险值测度建立零售商的风险损失目标,提出一种供应商与多个零售商的具有销售奖励契约的多随从双层风险决策模型,并提出了一种近似求解算法,通过给定的实际数据,运用模型可以获得供应商的奖励销售阈值、奖励折扣和订购量的最优策略。
风险估值VaR(Value at risk)是一种在风险市场条件下和给定的置信水平区间内,估计金融资产或证券投资在给定的时间内可能发生的市场风险,即可能遭受潜在的最大价值损失值,即资产损失的最高可能值。基于决策x下的β-VaR值可以表示为
αβ(x)=min{α|Pr[L(x,ξ)≤α]≥β}
(1)
式中:β(β∈(0,1])为给定的置信水平;L(x,ξ):Rm×Rn→R1为决策者的损失函数;x为决策变量;ξ∈Rn为随机变量。
Rockafellar等[58]提出了条件风险值模型(Conditional value at risk, CVaR)。CVaR是基于VaR表示下提出的另一种描述风险的工具,它具有许多的良好性质,避免了VaR一些缺陷,CVaR可以用来测量组合投资的市场风险,在给定的置信水平β下,描述组合投资x的损失超过VaR损失的累积损失,那么x决策下的β-CVaR值公式可以表示为

(2)
式中:F(·)为分布函数;CVaR值为损失函数L(x,ξ)超过VaR值时的累积期望损失,CVaR风险值描述了市场不确定下引起的累积损失,也可以用于研究供应链库存订购的风险决策问题。
2 基于奖励契约下的多随从双层条件风险值决策模型
为了激励零售商的销售量,制造商或供应商采用一种销售数量激励机制,称为销售奖励契约,即供应商采用统一的批发价,规定零售商按统一的销售价进行销售,当销售量超过一定量的话,供应商按一定的价格比例对零售商进行利润奖励,以刺激零售商想办法进行更多的销售。因此,供应商为了激励零售商更多的订货,制定销售奖励契约,所有零售商必须满足同一契约,鼓励零售商尽可能多销售,零售商希望从供应商处订购更多的产品,这样才有可能获得销售奖励,供应商对零售商实施销售奖励策略,不采用回购策略,供应商需要制定销售多少才给出相应的奖励,但是销售量奖励阈值不能确定过高,否则零售商不能完成,零售商不会积极地销售,或者订购更多的产品。
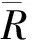
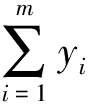
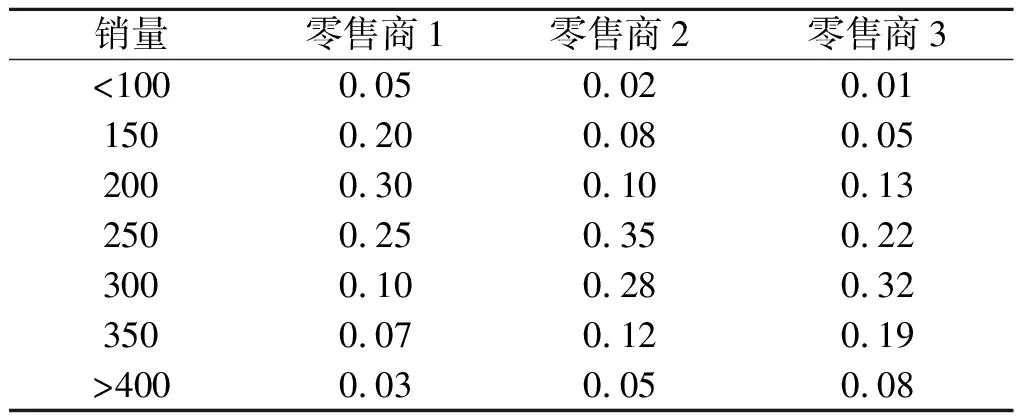
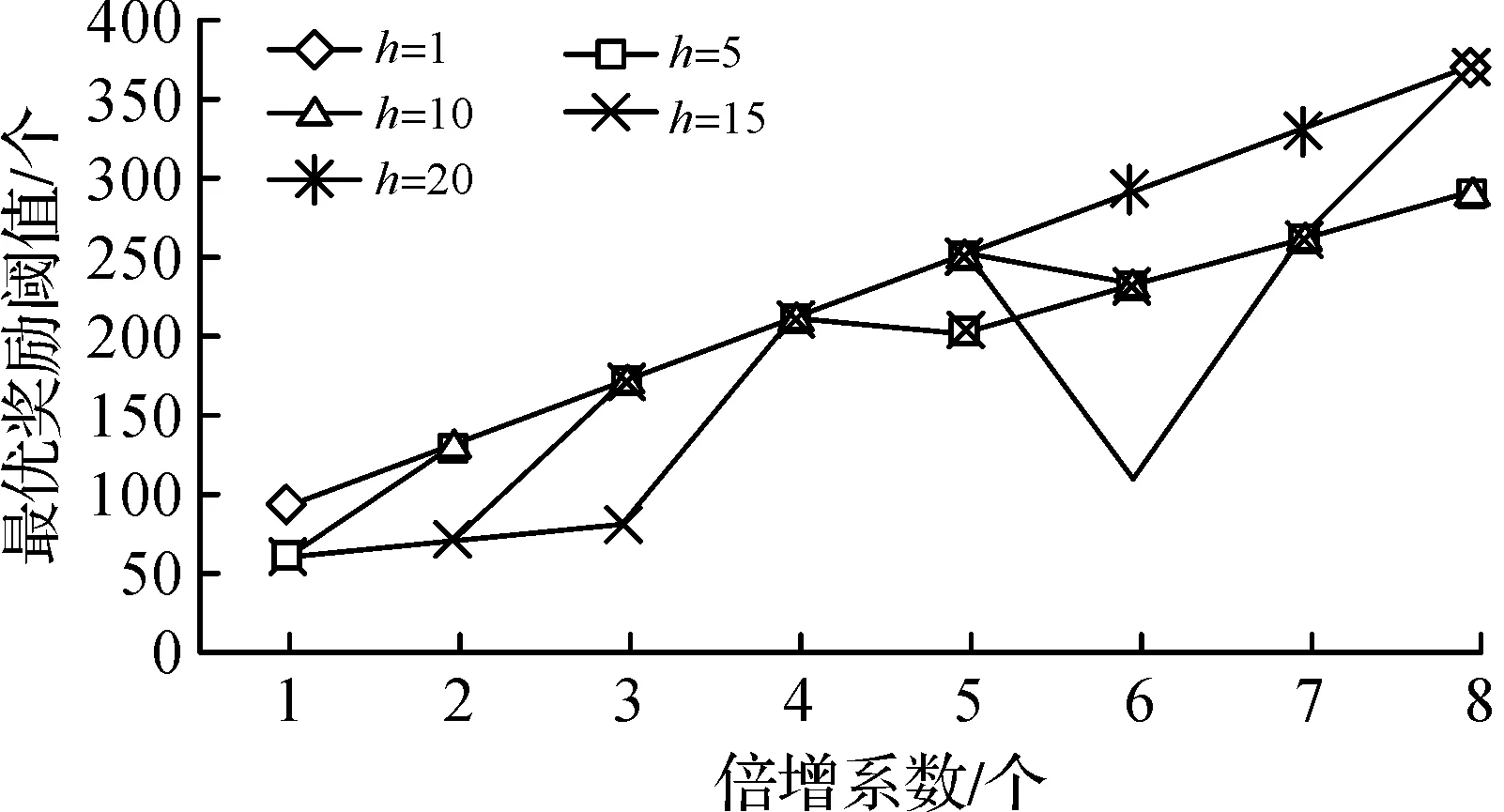
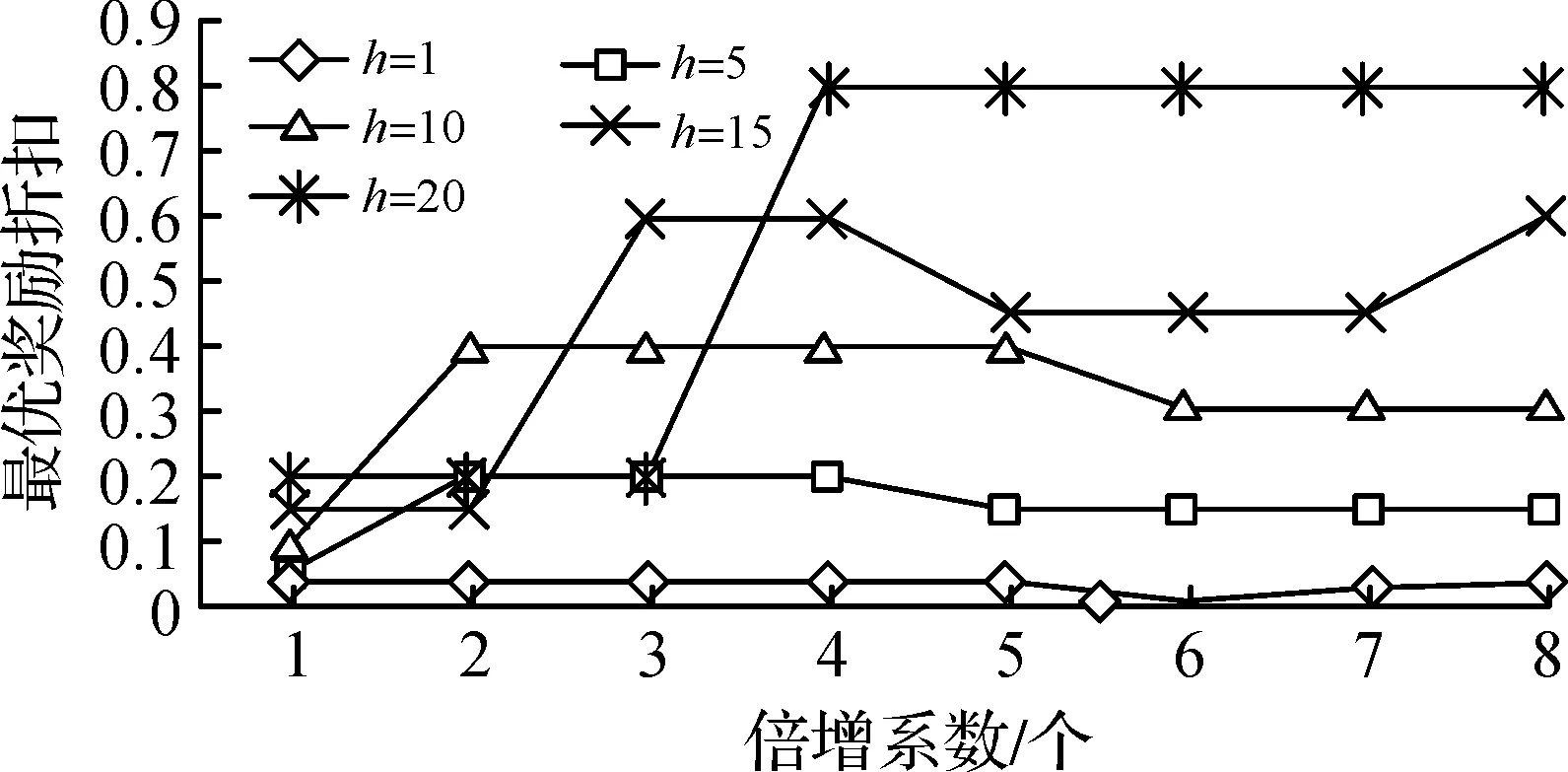
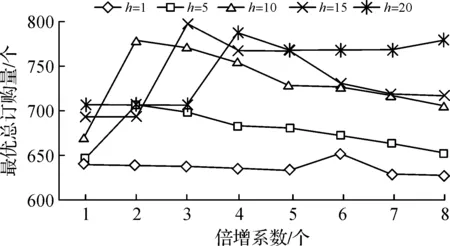
W={wj|j=0,1,2,…,n;0=w0< 假设市场需求信息是公开的,零售商在订货过程中,供应商对所有零售商实施相同的奖励策略,零售商根据市场预测,确定订货量yi;供应商则根据市场需求情况以及零售商的订货量确定批发价格。 当供应商给定批发价、奖励折扣和奖励阈值时,当供应商批发价为a时,第i个零售商的订货量为yi,供应商考虑期望收益最大化,即 (3) 式中:a为制造商或供应商确定商品批发价格;yi为第i个零售商根据批发价确定的订货量;w为供应商确定的销售量阈值,其中w属于给定的阈值集合W;r为奖励折扣(因子);供应商按商品每单位批发价a的ar元进行奖励,其中r属于折扣集合,即 式(3)中:ayi-arE(vi-w)+第1项为批发获得的利润,第2项为奖励损失,需要满足(w,r)∈{(wj,rj)|j=1,2,…,n}。 零售商订货yi单位时,零售商损失函数可以表示为 gi(w,r,yi,vi)=a(yi-vi)++(p- (4) 式中t+=max{t,0}。设Y为制造商提供零售商总的产品数量;p为零售商的产品零售价格;vi为第i个零售商产品需求(销售量),是一个随机变量;qi(vi)为第i个零售商产品需求对应的概率分布密度函数。式(4)中第1项为过剩损失,第2项为缺货损失,第3项为达不到奖励造成的奖励损失。给定置信水平αi(0<αi<1),定义第i(i=1,2,…,m)个零售商的VaR损失为 定义 得出结论为 则得到多随从双层规划: s.t.y1+y2+…+ym≤Y (w,r)∈{(wj,rj)|j=1,2,…,n} 对于i=1,2,…,m,(yi,ti)是问题Pi(w,r)的最优解,即 s.t. 0≤yi≤Y,ti∈R1 s.t.y1+y2+…+ym≤Y (w,r)∈{(wj,rj)|j=1,2,…,n} 对于i=1,2,…,m,(yi,ti)是下面问题Pi(w,r)的最优解,即 s.t. 0≤yi≤Y,ti∈R1 模型规划2中目标函数不是连续函数,由于奖励折扣一般仅为有限多个,采用下面一种近似计算方法: 1) 对每个i=1,2,…,m,求m个子问题Pi((wj,rj))′(j=1,2,…,m),若得到第i零售商在每个奖励(wj,rj)下的最优解(yi(wj,rj),ti(wj,rj))(j=1,2,…,m)。 2) 求问题的最优解,即 s.t.y1(w,r)+y2(w,r)+…+ym(w,r)≤Y (w,r)∈{(wj,rj)|j=1,2,…,n} 对一个面包制造商和它的三家零售店的批发和订购调研,获取了相应的数值,根据调查产品的历史销售样本数据,计算出了一个近似概率分布(表1)。 表1零售商的销量近似概率分布 Table1Distributionofsalesapproximationprobabilityoftheretailers 销量零售商1零售商2零售商3<1000.050.020.011500.200.080.052000.300.100.132500.250.350.223000.100.280.323500.070.120.19>4000.030.050.08 为了测试奖励对订购的影响,在表2中设h∈[1,20]为奖励折扣倍增系数,销售初始阈值增加系数k=1,2,3,4,5,6,7,8。已知数值实验,固定值为:批发价a=10元/个,零售价p=15元/个,总生产量为900,置信水平α=0.95。数值实验的目的是在不同奖励倍增系数确定供应商的最优奖励阈值、最优奖励折扣和生产总量范围,以及零售商的最优订购量。 表2产品的奖励契约阈值和奖励折扣范围 Table2Thethresholdsandtherangeofincentivediscountsfromthemanufacturer 销售阈值范围奖励折扣>50+10k0.01h>50+20k0.02h>50+30k0.03h>50+40k0.04h 首先,取几个不同的折扣因子,通过数值计算分析8个不同起始因子下供应商的最佳奖励阈值、最佳折扣和利润,以及零售商的最优订购量和风险损失变化。 图1中5个奖励倍增系数h分别为1,5,10,15,20,而8个奖励起始阈值系数k分别为1,2,…,8,其供应商的最优奖励阈值为w。从图1可以看出:一般当奖励起始阈值系数或奖励倍增系数增大,最优奖励起始阈值也增大,即提高奖励倍增系数或起始阈值系数可以显著提高最优奖励阈值。 图1 不同倍增系数下的最优奖励阈值变化Fig.1 Change in optimal reward threshold under different multiplication coefficients 图2为5个奖励倍增系数h,8个奖励起始阈值系数k的供应商的最优奖励折扣r,从图2可以看出:当奖励倍增系数h>15时,倍增系数增大时最优奖励折扣增大,此时,倍增系数对奖励折扣有显著影响,但当奖励倍增系数h<15,最优奖励折扣不变或减小,即此时倍增系数对奖励折扣没有影响,说明大的倍增系数有利于提高奖励折扣。 图2 不同倍增系数下的最优奖励折扣变化Fig.2 Changes in optimal reward discount under different multiplication coefficients 图3为5个奖励倍增系数h,8个奖励起始阈值系数k的零售商的最优订购总量y。从图3可以看出:当奖励倍增系数增大时零售商最优订购量增大,说明奖励折扣提高,零售商的订购量提高,但是当奖励倍增系数不变且奖励起始阈值系数增大时一般零售商的订购量会减小(如h=1,5,10,k>1),因为提高初始奖励阈值,零售商获得的销售奖励会减少。 图3 不同倍增系数下的最优总订购量变化Fig.3 Changes in optimal total order volume under different multiplication coefficients 图4为5个奖励倍增系数h,8个奖励起始阈值系数k的零售商的最优总损失。从图4可以看出:当奖励倍增系数h>10,增大倍增系数,零售商损失也会增大,说明虽然提高销售奖励倍增系数,但是起始阈值提高后,零售商需要完成更多的销售才能获得奖励;当h<10时,零售商损失随着倍增系数增大时增加很少,说明提高奖励折扣,零售商的风险损失会增大。 图4 不同倍增系数下的零售商最优总损失的变化Fig.4 Changes in the optimal total loss of retailers under different multiplication coefficients 图5为5个奖励倍增系数h,8个奖励起始阈值系数k的供应商的最优总利润。从图5可以看出:当奖励倍增系数增大h>10,倍增系数增大时,供应商总利润增大,当h<10时,供应商的总利润随着倍增系数增大反而增加很少,这时零售商获得奖励更多,说明提高奖励折扣,供应商的利润会增大。 图5 不同倍增系数下的供应商最优总利润的变化Fig.5 Optimal change of the supplier’s total profits under multiplication coefficients 从图1~5数值结果来看:初始奖励阈值增大,供应商的最佳奖励阈值和折扣也增大,供应商利润增大,但是零售商的损失风险会增大,零售商的总订购量会适当减少,零售商的总订购量不超过800,在奖励契约下,供应商不需要生产超过800的总量,总的生产量范围在700~800。供应商确定较高的奖励阈值和奖励折扣,零售商会提高订购量,但风险增大比较明显,供应商应根据零售商的风险来确定最优阈值和最优奖励折扣,以保证供应商自己能获得更多的利润。所以倍增系数影响了最优奖励阈值和奖励折扣的确定,在同一个初始奖励阈值,同批发折扣契约相比,销售奖励契约对激励零售商订购量增加的影响不如批发折扣契约。 通过模型规划2数值实验,总结了如何使用模型规划2进行奖励批折扣契约制定,注意有3点: 1) 收集销售数据,计算需求概率分布,确定订购量范围与对应的起始奖励阈值范围和对应的奖励折扣倍增系数。 2) 确定起始奖励阈值,首先在不同的总产量下,计算不同奖励阈值下的最优奖励折扣和订购量,比较供应商的利润和零售商的风险,确定供应商的起始奖励阈值和生产总量范围。 3) 确定最优奖励折扣与最优订购量,取置信水平0.95~0.99,在给定的起始奖励下计算最优奖励阈值、奖励折扣和订购量,通过给定供应商的期望利润目标和零售商的风险目标,确定在某个起始阈值下的供应商最优批发折扣和零售商最优订购量范围。 建立销售奖励契约的多随从双层条件风险值模型和计算方法,销售奖励目标的总订购量决定了生产商的总产量,销售奖励最低阈值不能过低或过高,通过降低奖励阈值和提高奖励倍增系数来增加零售商的订购量,但即使奖励阈值很低或奖励倍增系数很大,零售商的总订购量不会大幅度提高,因为受到销售需求限制,零售商提高订购量会增加供给过剩的需求,导致损失。因此,销售奖励契约模型可以确定最优的销售阈值和倍增折扣,以保证供应商有更多利润,保证零售商有更低的风险损失。
w1

a+ar)(vi-yi)++ar(w-vi)+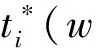
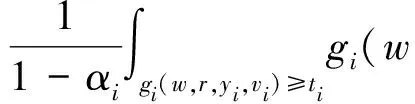


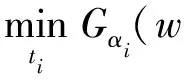
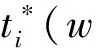
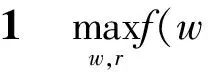


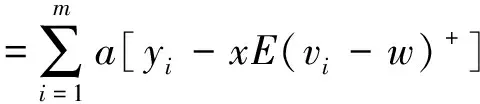


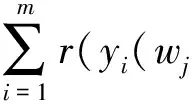
3 数值案例



4 结 论
