基于改进人工势场的变形移动机器人路径规划
2019-03-18王领宫涛樊庆琢郑义
王领 宫涛 樊庆琢 郑义


一、引言
人工势场算法是—种常见的路径规划算法,该算法在数学公式的描述上简洁,计算量较小,并且产生的路径路线比较平滑。在路径的生成上系统与环境实现了闭环,使系统的实用性和避障功能得到了加强。但是,通过研究发现,传统的人工势场存在以下问题。
(1)在相近障碍物间不能发现路径。
(2)存在陷阱区域。
(3)在障碍物前振荡。
(4)在狭窄通道中摆动。
(5)当目标附近有障碍物时无法达到目标点(GNRON)。
(6)规划的路径只考虑的路径的安全性,并没有对路径进行优化。
由于以上问题的出现,在极个别的实际应用场合,规划无法完成。通过数学分析,得知当障碍物与目标点十分接近的时候,此时机器人接近目标时,他同时也靠近障碍物,如果此时的排斥力大于吸引力,目标位置不能到达全局最小势场,因而机器人停在障碍物附近不可能达到目标,即机器人的不可达问题(GNRON)。这是由于传统的人工势场算法存在缺陷,使该方法在处理具体问题中存在一定的局限性。因此,对传统的人工势场算法进行改进,特别对斥力场函数进行修改,使用改进后的模型进行路径规划,能够较好的解决传统模型缺陷带来的目标不可到達问题。
二、传统的人工势场模型
将人工势场法应用于路径规划是由Khatib首先提出的。他把机械手或者是移动机器人在环境中的运动视为在一种抽象的人造受力场中运动:目标点对机器人产生引力,障碍物对机器人产生斥力,最后根据合力来确定机器人的运动。
人工势场法的基本思想:在目标位置构造引力势场,在障碍物周围构造斥力势场,这两个势场共同作用形成复合人工势场。机器人在引力势场的引力和斥力势场的斥力的共同作用下向目标运动。
我们把移动机器人、障碍物和目标点均简化为一点,机器人的运动空间为二维的。机器人要到达目标点,需要不断朝着目标点运动,因此,可以将目标点看作与移动机器人带有相反极性的电荷,对机器人产生吸引力。同时由于机器人在运动过程中需要避开障碍物,因此,可以将障碍物看作与机器人带有相同极性的电荷,对机器人具有排斥力,从而使机器人避开障碍物。同时,假设起始点带有与机器人极性相同的电荷,从而开始规划开始的时候推动机器人运动。
三、改进的人工势场模型
如果机器人的目标点在障碍物的影响范围之内,整个环境势场的全局最小点就与目标点的位置不一致,这样,当机器人靠近目标点的同时,斥力不断增大,这就造成了不可达问题。
考虑到不能到达问题是由于在目标点处的势场斥力函数过大造成的,考虑将斥力场函数与机器人和目标点的相对位置考虑在内,通过这个方式对斥力场函数进行体整,以保证全局势场在目标点处为最小。
四、变形移动机器人的路径规划
我们把变形移动机器人看成一个点,如图1所示,由目标点对移动机器人产生的引力Fatt,它是引力势场函数的负梯度,即为:
五、仿真试验
在建立的人工势场模型的基础上对变形移动机器人进行路径规划,机器人从起点开始,受到的合力作用下朝目标点进发,引力随着机器人的靠近而减小,在全局范围内为机器人导航,而障碍物的斥力随距离的增减变化,但只有一定的作用范围,因此对于每一个障碍物,其斥力仅在其周边局部区域为机器人导航。具体的路径规划算法步骤如下。
(1)建立人工势场模型,初始化移动变形机器人的参数,确定引力场和斥力场的正比例位置增益系数k和η,障碍物影响距离Po,以及移动步长l,(设定机器人匀速前进)的值。同时确定机器人起始位置x,按照具体的环境信息建立势场模型。
(2)调用计算模块,计算斥力和引力与x轴的角度,计算引力、斥力在x,y轴的分量,计算合力,计算合力与x轴的夹角。
(5)判断机器人是否到达目标点,如果到达目标点,则终止规划过程。
(6)如果机器人没有到达目标点,再判断前进步数是否到达规定步数,如果到达则表明无法找到完整路径,需要调整模型参数,否则就返回第三步继续执行。
下面讨论不同的初始参数下得到仿真结果。
1、多障碍物情况下的仿真
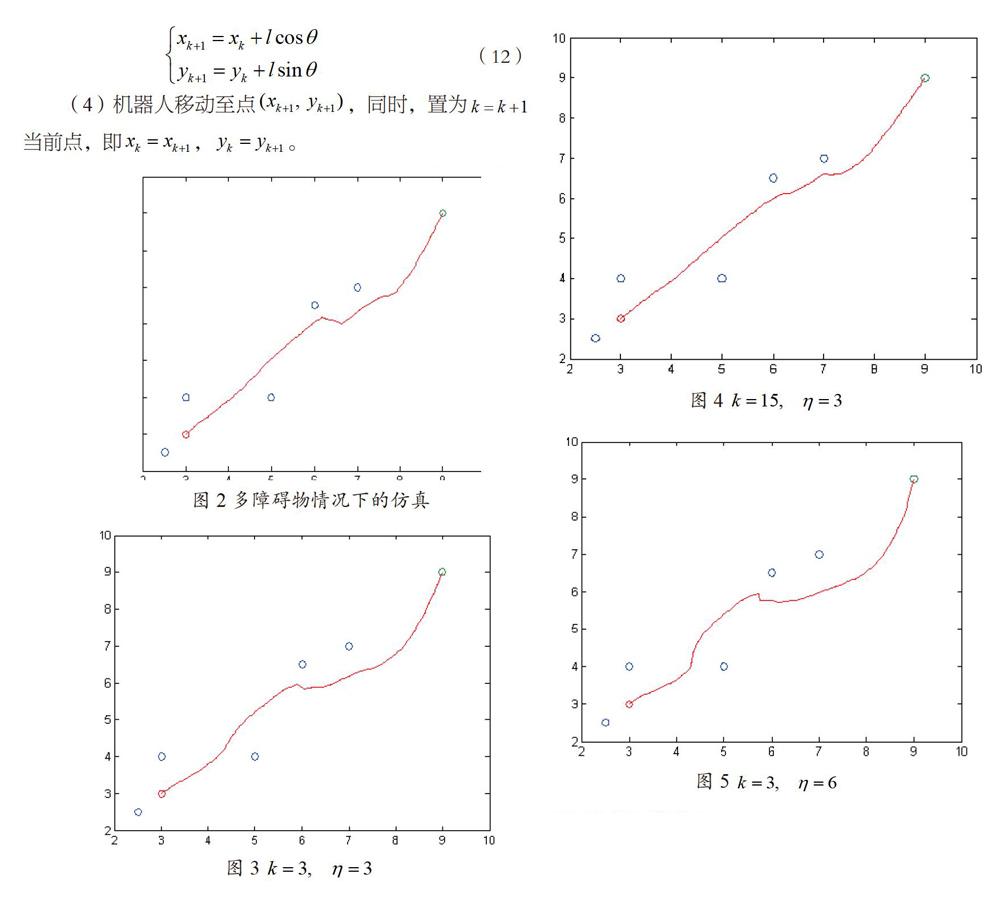
利用MATLAB软件进行仿真试验,如图2所示,起始点为[3,3],障碍物为[2.5,2.5]、[3,4]、[5,4]、[6,6.5]和[7,7],目标点为[9,9],引力场的正比例增益系数k为3,斥力场的正比例增益系数η为1,障碍物影响距离Po为3,移动步长l设为0.5,得到如图2所示的路径仿真结果。
2、不同的引力场和斥力场的正比例增益系数下的仿真
起始点为[3,3],障碍物为[2.5,2.5]、[3,4]、[5,4]、[6,6.5]和[7,7],目标点为[9,9],障碍物影响距离Po为3,移动步长,设为0.2,不同的n和η对仿真结果有不同的影响,具体如图3~5所示。
3、不同步长下的仿真
起始点为[3,3],障碍物为[2.5,2.5]、[3,4]、[5,4]、[6,6.5]和[7,7],目标点为[9,9],引力场的正比例增益系数k为6,斥力场的正比例增益系数η为3,障碍物影响距离po为3,不同的移动步长对仿真结果有不同的影响,具体如图6-8所示。
六、结论
对利用传统人工势场模型进行移动机器人路径规划的缺陷进行了数学分析,由于该缺陷的存在,在特定的环境中会产生不可到达问题。通过对斥力函数的修正,得到了改进的人工势场模型,实验表明,运用改进后的势场模型能够进行准确的路径规划。
