华中地区经济周期与电力需求周期的特征及相互关系
2019-03-18徐斯旸祝志刚
徐斯旸 ,祝志刚
(1.广东金融学院 金融与投资学院,广东 广州 510521 ;2.中南财经政法大学 金融学院,湖北 武汉 430073;3.国家电网公司华中分部,湖北 武汉 430077)
电力因其应用的广泛性及有限的替代性而成为极具战略重要性的资源。然而,电力无法经济地大规模存储以及只能通过输电网络和配电网络输送的特性,要求电力生产与消费必须实现实时平衡,这是电力系统和电力市场安全稳定运行的重要前提。既要防止电力需求水平预测过低带来的缺电现象频发对经济社会发展造成制约,又要避免电力需求水平预测过高造成的过度投资以及供给过剩导致的运行效率低下。因此,电力需求预测是一个非常重要的问题,以最佳方式管理电力资源成为电力规划者和政策制定者的当务之急。
从我国电力市场的运行情况来看,2017年1—12月全国发电量剩余131.5×109kWh,各地用电缺口不一。面对新时代高质量发展提出的要求,深化供给侧结构性改革背景下,“三去一降一补”不断推进,增长动力不断转换,经济结构不断优化,能源消费增长步入“中高速”,新的重点电力消费部门正在形成,电力需求预测方法也必须与时俱进。
电力市场需求与社会经济活动密切相关,而经济活动又体现为由诸多影响因素触发的规律性活动。例如,以美国为背景的研究发现,随着市场化进程的推进,电力消费与经济周期的关联更为紧密。因此,研究宏观经济运行的特征,尤其是在当前供给侧改革政策下的新周期变化,分析电力需求变化特征及其与经济发展的相互关系,将会为电力需求预测提供较为科学的依据,促进经济与电力能源的可持续性发展。当宏观经济与电力需求周期之间存在长期均衡关系时,有助于优化电力需求预测结果。
经济活动的规律性波动,又称经济周期,是指经济运行中周期性出现经济扩张和经济紧缩交替更迭、循环往复的一种现象。自从美国国家经济研究局Burns & Mitchell提出经济周期阶段的具体描述和度量以来,经济周期波动的机制得到了广泛深入的研究。经典的经济周期分析模式主要根据经济增长速度的高低、不同周期阶段的持续时间、经济周期扩张和紧缩的转变点等来刻画经济周期波动的主要特征。从对经济波动的认识上来看,早期的理论把波动解释为不同长度的、规则性的周期组合,如基钦周期、朱格拉周期、库兹涅茨周期和康德拉季耶夫周期;现代宏观经济理论认为就波动幅度和持续时间长短而言,波动不表现出简单的规则或周期模式,经济周期从本质上被认为是类型和大小各异的随机扰动因素被放大后导致的总量经济运行结果,经济周期应该更多地被理解为宏观经济时间序列之间的共变性,而非结果意义上的产出水平在时间长度和波动幅度上的规则性[1-2]。本文选取经济增长率作为衡量指标刻画经济周期波动,利用H-P滤波法、协整检验和谱分析方法,就经济周期与电力需求之间的关联展开系统的研究。
1 研究现状
电力需求与经济发展的关系一直是近十多年来的研究热点,国内外有众多学者进行了大量研究,目前仍未形成一个普遍认可的结论。不同于西方发达国家电力负荷与需求趋于稳定,中国的经济结构随着改革深入发生着深刻变化,电力需求预测存在很大的挑战性[3]。因此,应用国外成功的方法对中国中长期电力需求进行预测是比较困难的,国内学者结合中国实际情况积极探索新的预测方法[4]。
文献[5]利用协整分析和向量误差校正模型,证明中国电力需求与GDP、固定资产投资等经济因素之间具有长期的均衡关系,并通过Granger因果关系,检验证明它们之间是双向且长期稳定的因果关系。文献[6]将H-P滤波法用于中国电力需求的趋势和周期成分分解,并应用谱分析方法从频域研究了中国电力需求的时间序列,采用聚类和相关分析方法得到对全国电力需求周期影响较大的省份。文献[7]使用H-P滤波法将中国GDP和电力消费分解成趋势和周期成分,得出电力和经济的协整关系与经济的周期性波动有关。文献[8]应用谱分析方法,研究了能源消费增速、碳排放、节能率等指标与中国经济增长的长期关系。文献[9]采用自回归分布滞后模型的边限协整检验和基于误差修正模型的Granger因果检验方法,对中国电力消费和经济增长进行因果关系实证研究,结果表明电力消费与经济发展有显著的单向长期因果关系,两者的周期波动之间存在明显的双向因果关系。文献[10]基于协整检验、Granger因果关系检验、脉冲响应和灰色关联度分析等方法建立了电力消费与经济增长关联关系的研究方法,以无锡地区数据验证了该方法的正确性。
谱分析方法将时间序列分解成互不相关频率的分量,研究其周期变化和主要周期波动特征,该方法在经济和电力需求分析中的有效性已经得到验证。交叉谱分析可以得到各周期分量之间的相对重要程度及相互领先或滞后时间,适于研究经济周期和电力需求周期关系。本文以华中地区4个省份为例,研究其经济和电力需求的周期关系,为进一步预测该地区的电力需求提供指导。
2 研究方法与应用数据
本文以华中地区(河南、湖北、湖南和江西4省)生产总值和地区用电量时间序列作为分析对象,原始数据来源于国家统计局国家数据官方网站,选取1995—2016年华中地区4个省份生产总值和地区用电总量,如图1所示。

(a)生产总值

(b)电力消费总量图1 华中地区生产总值和电力消费总量Fig.1 GDP and total electricity consumption in Central China
本文主要运用H-P滤波法和谱分析法检验华中地区经济周期和电力消费特征。
2.1 H-P滤波法
H-P滤波法是由Hodrick和Prescott于1980年提出的,被广泛地应用于研究宏观经济趋势。H-P滤波可以看作是一种高通滤波器,其理论基础是时间序列的谱分析方法。谱分析方法把时间序列看作是不同频率成分的叠加,H-P滤波就是分离出高频成分,去除低频成分,即去掉长期趋势分量,从而对中短期随机波动进行研究。H-P滤波的基本原理可以表述如下:
H-P滤波将时间序列Y={y1,y2,…,yN}分解成趋势分量T={t1,t2,…,tN}和周期分量C={c1,c2,…,cN},N为样本容量。采用加法模型,H-P滤波将yi(i=1,…,N)分解为
yi=gi+ci.
(1)
式中gi和ci均为不可观测值。
HP滤波的目标函数为
(2)
式中λ为平滑参数。该规划问题就是对所有ti最小化目标函数。第1个求和项最小化时间序列和趋势分量之间的差(即周期分量),第2个求和项最小化趋势分量的二阶差分。如果λ=0,则H-P滤波退化为最小二乘法。
2.2 谱分析法
谱分析是对单个或者多个时间序列对应的谱、增益、相关性等进行估计,然后运用估计值分析存在于时间序列的行为过程。谱分析从频域观察时间序列,将其看成是由不同频率的规则波叠加而成,通过研究和比较不同频率波方差的大小和频率分量的周期变化,揭示时间序列的频率结构,掌握其主要波动特征和周期。
2.2.1 单谱分析
单谱分析用于估计单个时间序列剔除趋势因素后的周期波动成分,从估计出的谱密度函数中获取序列的主要频率成分,掌握序列的周期波动特征。
在谱分析中,通常采用傅里叶级数来拟合yi,即
(i=1,2,…,N).
(3)
式中:a0为总体平均值;εi为具有零均值的独立同分布高斯随机变量的白噪声序列;K为傅里叶级数索引,K=1,2,…,n,n=N/2;aK、bK为傅里叶级数方程的拟合系数。
拟合公式中系数的计算公式为
(4)
2.2.2 交叉谱分析
在谱分析中,为了研究2个及以上平稳时间序列在频域上的关系,一般采用交叉谱分析,它可以用来研究时间序列中各响应频率分量所对应的周期波动关系。
设xt为一个协方差平稳的m×1向量过程,其期望值记为E(xt)=μ,第k阶自协方差为
Rx(k)=E[(xt-μ)(xt-μ)T].
(5)
假设自协方差矩阵具有绝对可加性,则其多元总体谱
(6)
式中ω为频率。
在多元谱Px(ω)中,其主对角线上的元素P11(ω),…,Pmm(ω)都为实数,称为自谱;主对角线外的元素Pjk(ω)(j≠k)称为交叉谱,交叉谱一般是复数,其实部为反映序列同相频率分量相关性的余谱,虚部为反映序列异相频率成分相关性的积谱。
用极坐标形式表示交叉谱,极坐标的振幅Ajk(ω)称为增益,
表1 Johansen协整检验结果
Tab.1 Johansen co-integration test results
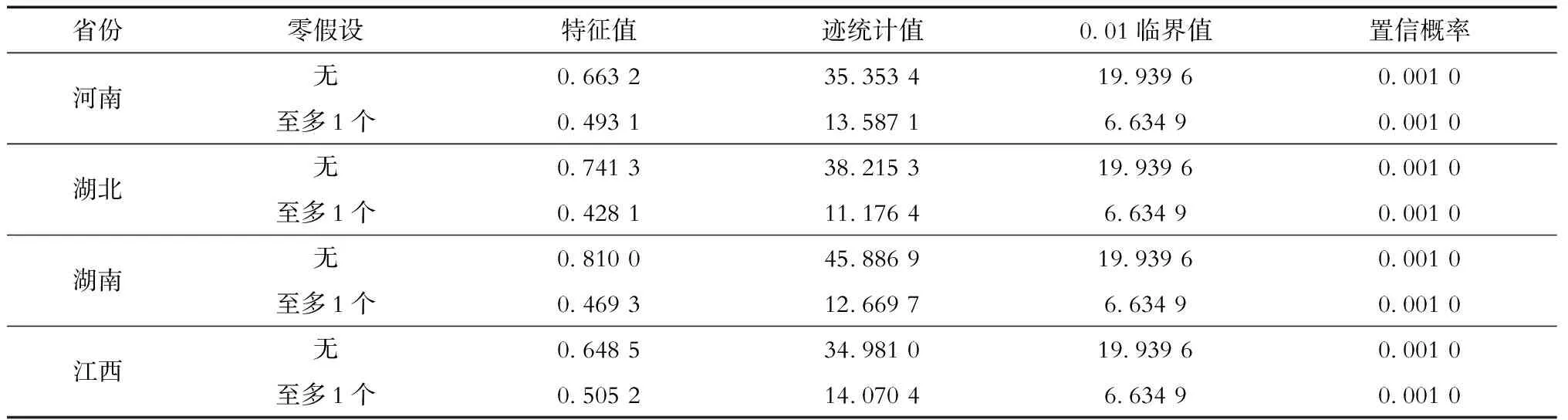
省份零假设特征值迹统计值0.01临界值置信概率河南无0.663 235.353 419.939 60.001 0至多1个0.493 113.587 16.634 90.001 0湖北无0.741 338.215 319.939 60.001 0至多1个0.428 111.176 46.634 90.001 0湖南无0.810 045.886 919.939 60.001 0至多1个0.469 312.669 76.634 90.001 0江西无0.648 534.981 019.939 60.001 0至多1个0.505 214.070 46.634 90.001 0
(7)
极坐标的角度称为相位谱,即2个序列中对应频率分量相位变化的矩阵,反映了序列各频率分量的相位差领先或滞后关系,通常限定在区间[-π,π]内,其计算公式为
(8)

(9)
凝聚谱Cjk(ω)的数值如果比较大,则表示序列有频率为ω的重要共同周期。
电力需求和经济发展一样,在长期增长趋势下,伴随着中短期的周期性波动态势。为了深入了解电力需求的周期特征,有必要将电力需求时间序列进行趋势成分和周期成分的分解,分析其与宏观经济运行周期特征之间的关系。
电力需求和经济时间序列通常是非平稳的,使用平稳数据变量的经典回归模型会出现虚假回归等现象。但是,如果变量之间有长期稳定关系,即协整关系,则可以使用经典回归方法建立模型。为此,要检验电力需求和宏观经济周期之间是否存在长期稳定关系。
3 经济周期与电力消费特征
3.1 H-P滤波法结果
H-P滤波法要求时间序列具有平稳性。首先,对华中地区生产总值和电力消费总量序列取对数后再差分;然后使用H-P滤波法分解,所得的各省生产总值和电力消费的周期成分序列经ADF单位根检验方法检验,在1%的显著性水平下为平稳序列;最后,对各省生产总值和电力消费的周期成分序列进行Johansen协整检验,在1%的显著性水平下,迹检验的结果表明各省生产总值的周期成分和电力消费的周期成分之间存在协整关系,见表1。
华中地区经济增长率、电力消费增长率的趋势和周期分解如图2、图3所示。以2008年美国次贷危机引发的全球金融危机为转折点,华中地区生产总值的增长率呈现下降趋势,其中湖北下降相对缓慢;华中地区电力消费的增长率同样出现下滑迹象。仅从周期波动成分来看,华中地区生成总值的增长率波动保持较好的一致性,而电力消费的增长率波动呈现出各自特点。2008年全球金融危机对中国各地区经济产生了影响,同时中国开启了深化经济体制改革,进行产业结构性调整,尤其是供给侧结构性改革,强调要逐渐将经济增长速度控制在合理范围内。可以看出,华中地区经济增长率也受到了国际经济大环境和国家政策调整的影响。
3.2 谱分析法结果
首先对华中地区经济增长率的周期成分进行单谱分析,在表2中列出了频谱计算结果。河南经济增长率的长周期波动长度约为12.8 a,湖北、湖南和江西经济增长率的长周期波动长度约为14.2 a,同时4省短周期波动长度约为3.6 a,谱密度值也比较大。华中地区经济发展水平介于经济发达和落后地区之间,经济发展速度较快,因而经济波动较为频繁,同时经济发展有逐步平稳的趋势,这与文献[8]分析得到的结论一致。
表4 2017年度华中地区生产总值和电力消费预测值与实际值对比
Tab.4 Comparison of prediction values and actual values of GDP and electricity consumption in 2017 in Central China

省份生产总值预测值/万亿元实际值/万亿元误差/%电力消费总量预测值/109 kWh实际值/109 kWh误差/%河南4.468 6554.498 816-0.67320.670316.6171.28湖北3.707 1283.652 2951.50188.406186.9000.81湖南3.491 2113.459 0560.93157.916158.151-0.15江西2.045 4092.081 850-1.75141.682129.3989.49
注:实际值的数据来源Wind。

(a)趋势成分
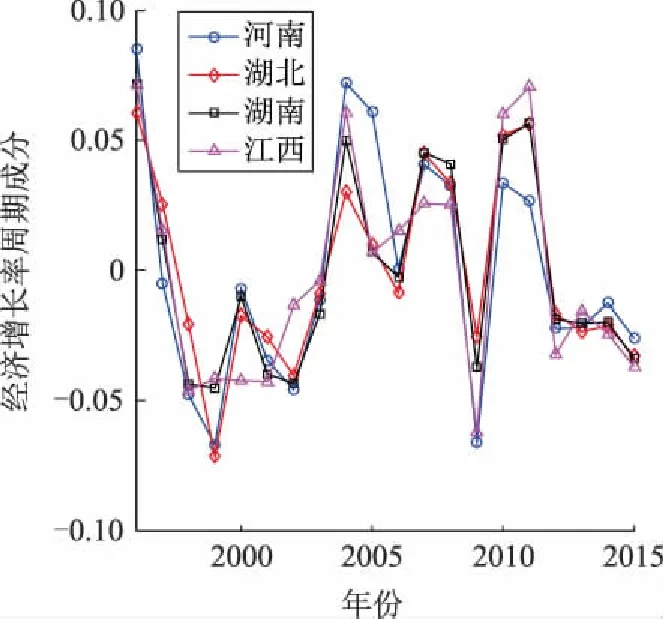
(b)周期成分图2 华中地区经济增长率的趋势和周期分解Fig.2 Trend and periodic decomposition of economic growth rate in Central China

(a)趋势成分

(b)周期成分图3 华中地区电力消费增长率的趋势和周期分解Fig.3 Trend and periodic decomposition of electricity consumption growth rate in Central China
表2 华中地区经济增长率周期成分单谱分析
Tab.2 Single spectrum analysis of periodic component of economic growth rate in Central China

地区主峰频率谱密度主周期波动长度/a河南0.078 130.005 35712.8湖北0.070 310.005 15514.2湖南0.070 310.005 21714.2江西0.070 310.046 24014.2
然后使用交叉谱分析,分别计算华中地区各省经济和电力消费增长率成对指标间的周期波动关系,见表3。从一致性上看,河南、湖南和江西在短周期长度时的电力消费增长率与经济增长率一致性最大,湖北在长周期和短周期长度时的一致性较接近;在长周期和短周期尺度下,电力消费增长率均领先于经济增长率,领先时间约为0.34~ 0.61 a,尽管湖南在长周期时领先2.29 a,但是其经济和电力消费相关性较低。
表3 华中地区经济和电力消费周期成分交叉谱分析
Tab.3 Cross spectrum analysis of periodic components of economic and electricity consumption in Central China
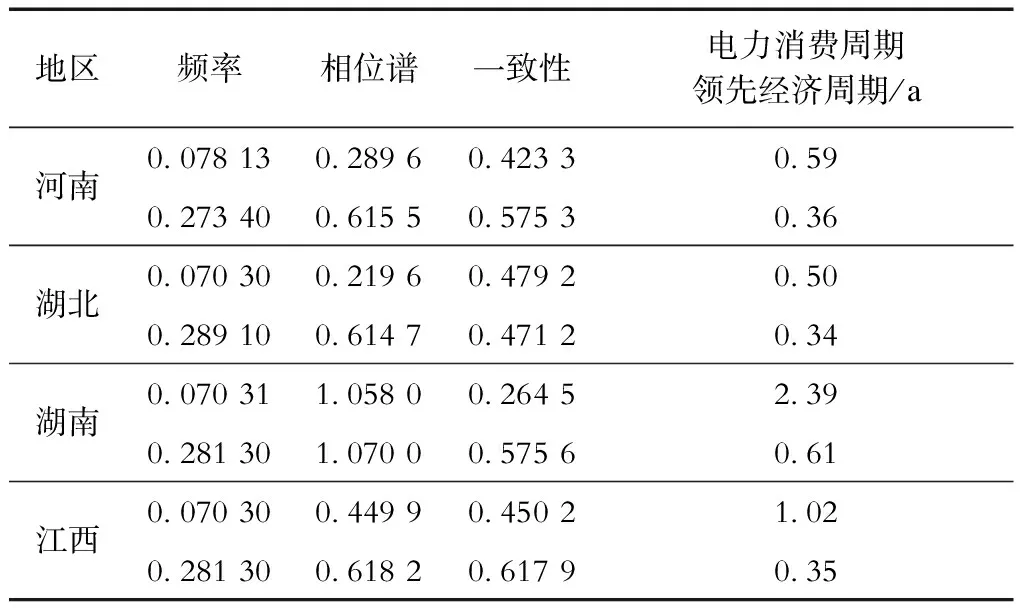
地区频率相位谱一致性电力消费周期领先经济周期/a河南0.078 130.289 60.423 30.590.273 400.615 50.575 30.36湖北0.070 300.219 60.479 20.500.289 100.614 70.471 20.34湖南0.070 311.058 00.264 52.390.281 301.070 00.575 60.61江西0.070 300.449 90.450 21.020.281 300.618 20.617 90.35
华中地区4个省份由于经济发展水平、产业结构布局各异,对电力的需求有各自特点,例如河南尽管经济总量高于湖北、湖南和江西,但是单位经济产值消耗的电力资源明显高于另外3省。相对而言,湖南的电力消费弹性系数最低,值得关注。
4 经济增长与电力需求预测研究
华中地区各省生产总值的周期成分和电力消费的周期成分之间存在协整关系,因此经济周期和电力消费周期之间既有共同的长期增长趋势,也有相关性较高的短期波动特点。因此,拟采用经济指标和电力消费数据共同来预测电力消费。
对华中地区经济增长率和电力需求增长率的趋势成分和周期成分分别采用多项式拟合和向量误差模型拟合,在此基础上应用向量误差修正模型,预测华中地区4个省份生产总值和电力消费总量。计算比较发现,当多项式的阶数为4时,拟合效果较好。使用MATLAB金融工具箱,向量误差修正模型为VEC(2),以1995—2016年的数据为样本,预测华中地区2017—2020年生产总值和电力消费总量,如图4所示。同时,对2017年度的生产总值和电力消费总量的预测值和实际值进行比较(见表4),除江西电力消费预测误差较大外,总体来说预测结果与实际情况吻合较好。由表2可知,江西经济波动主周期约为14.2 a,而由表3得到电力消费周期领先经济周期约1 a,因此2004年江西的电力消费突变数据将影响2017年电力消费总量的预测结果,导致最终的预测误差较大。事实上,从图3(b)可以发现,江西在2004年电力消费出现突然性的增加,然而随后的经济指标并未相应地突变,显然在这一预测过程中经济数据的平稳变化并未帮助更好地预测电力消费总量。文献[11]指出,在进行中长期电力需求预测时,考虑经济周期的影响需要慎之又慎,本文的分析结果印证了该结论。
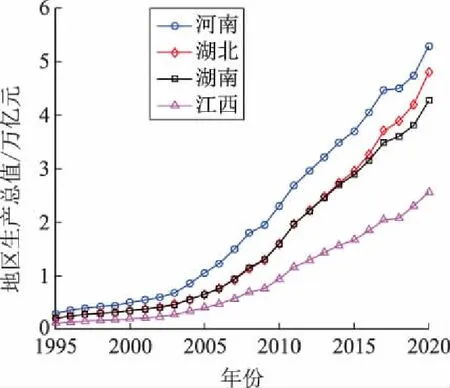
(a)生产总值

(b)电力消费总量图4 华中地区生产总值和电力消费总量预测Fig.4 Prediction of GDP and total electricity consumption in Central China
5 结论
电力工业是国民经济的重要基础,随着我国经济的发展,电力市场需求波动特性趋于复杂化,与国民经济的发展联系更是紧密。然而,由于当前我国电力工业与国民经济发展不均衡,造成了电力供应严重过剩现象,其中一个重要原因就是对电力需求的特征认识不足。因此,研究宏观经济运行的特征,结合当前供给侧改革政策下的新周期变化,分析电力需求变化特征及其与经济发展的相互关系,将会为电力需求预测提供较为科学的依据,促进经济与能源的可持续性发展[12-20]。
本文利用谱分析方法研究华中地区经济和电力需求之间的关系,得出以下结论和建议:
a)华中地区4个省份的经济发展长周期较长(超过12 a),短周期比较接近(约为3.6 a),并且短周期谱密度较大,反映了该地区经济水平发展正在快速提升。
b)通过交叉谱分析,可知华中地区4个省份的经济周期和电力需求周期波动关系比较密切,普遍存在电力需求周期领先于经济周期的现象,领先期为0.34~0.61 a。
c)建立华中地区各省的经济周期和电力需求周期的向量误差修正模型,对2017—2020年的各省经济总值和电力消费总量进行预测,对比2017年的实际值,预测趋势正确,结果准确度高。同时,也存在预测误差较大的情况,说明仅用这2个指标很难反映复杂多变的经济和电力需求关系。
在今后的研究中,需要考虑更多宏观经济指标的影响和电力需求的行业差异,进一步深入研究电力需求和宏观经济各重要指标的相互关系,以便为电力需求分析和预测提供更准确的指导,促进国民经济和电力市场的稳定和可持续发展。
