某小型通用发动机动平衡分析及其对策
2019-03-18刘永根杨海岳
刘永根 杨海岳 李 进
(浙江中坚科技股份有限公司 浙江 永康 321300)
引言
某小型通用发动机是单缸、风冷、四冲程发动机。发动机曲轴连杆机构运动所产生的往复惯性力和旋转惯性力是整车重要的振动源,可以通过对其进行动平衡分析,指出曲轴在结构设计上的不足之处,并提出在最少改变现有结构条件下的对策。
1 单缸发动机动平衡简要分析
发动机工作时,曲柄连杆机构作复合平面运动。在力学上可采用双集中质量系统来替代实际机构的质量分布,即一部分作为往复直线运动的质量mj,包括活塞组质量mp和连杆组换算到小头中心的质量m1,它们集中作用在活塞销中心,会产生直线往复惯性力Pj。另一部分为作旋转运动的不平衡质量mr,包括曲柄销换算质量mk、滚针轴承质量mg及连杆组换算到大头中心的质量m2,它们集中作用于曲柄销中心,会产生离心惯性力Pr。往复惯性力Pj和离心惯性力Pr按一定的周期交变地作用在发动机上,引起整机振动,使机器的平顺性和舒适性大大降低。
1.1 往复惯性力P j

一般只取Ⅰ级往复惯性力PjⅠ分析已足够,即方向沿着气缸中心线。

1.2 离心惯性力P r

方向始终沿曲柄向外
由式(3)可知,若ω以某一恒定速度运转时,Pr为一个大小不变的力[1]。
若要完全平衡Pj和Pr,则须配备结构复杂的双曲轴平衡机构,即在气缸中心线的两侧对称安装两对带平衡重的平衡轴。该方法所占空间较大,对小型发动机而言不切实际。一般多用简单的过量平衡,即在曲轴上装置较大的平衡重,此平衡重旋转产生的离心力Pd,不仅平衡了离心惯性力Pr,还存在剩余离心力ΔP=Pd-Pr,使其在Y轴(气缸中心线方向)的分力ΔP cosα来平衡掉一部分Pj,但在X轴方向同时出现不平衡力ΔP sinα。实际上是将Pj中的一部分力从Y轴上转移到X轴方向上,从而使振动的峰值减小(如图1所示)。

图1 平衡机构示意图

剩余离心力ΔP与一阶往复惯性力Pj的合力在X、Y轴上的投影为:

从上两式中消去α得:

可知F矢量端轨迹是一个椭圆(如图2所示)。
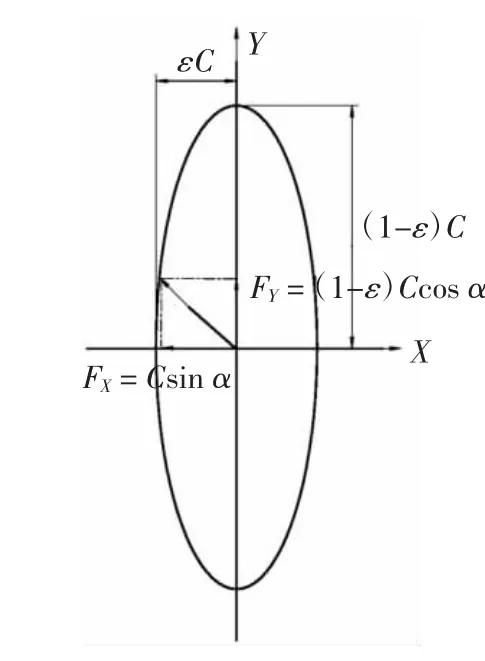
图2 F矢量端轨迹
一般总是希望较大的惯性力,即椭圆的长轴方向,放在发动机刚度较大的方向或吸振能力较好的方向[2]。
2 某小型通用发动机动平衡计算
运用上述动平衡分析理论,通过电子秤和Pro/E软件中的三维造型模型分析功能可知,活塞组质量mP=204 g。连杆总重mL=220.6 g,换算成大小头质量后即大头质量m2为139 g,小头质量m1为80.6 g。曲柄销质量mk=279 g,挡圈质量mq=2.6×2=5.2 g(2个),滚针轴承质量mg=45 g。
2.1 离心质量

离心质量产生的惯性力:

2.2 往复质量

往复质量产生的惯性力:

2.3 平衡质量
运用Pro/E软件中的模型分析功能
可求得平衡块的质量和质心(如图3所示)。
即md=1394.5(g),质心坐标(X,Y)为(-1.4,-6.73),求得质心与曲柄旋转中心距离:
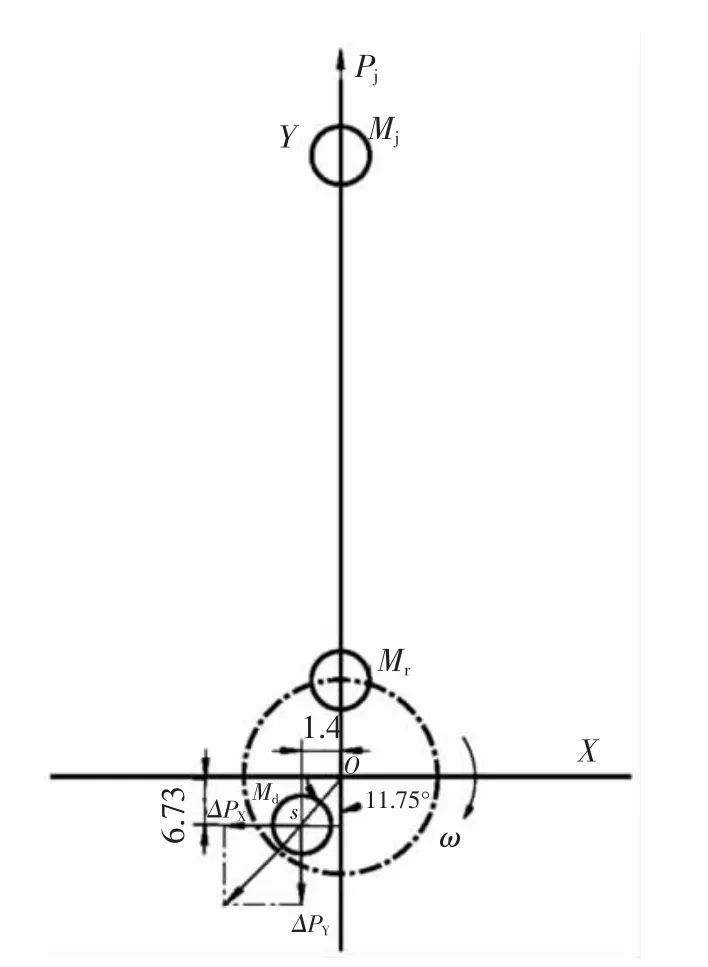
图3 平衡块的质量和质心(上止点位置时)

平衡质量产生的惯性力:

2 .4 动平衡分析
平衡质量产生的惯性力有两种作用。一部分用来平衡离心惯性力Pr,另一部分用来平衡往复惯性力Pj。
平衡质量平衡了离心惯性力Pr后剩余的离心力投影(如图4所示)。

图4 剩余离心力投影
在Y轴上:

在X轴上:

则剩余合力:

即平衡质量除平衡离心惯性力Pr外,还剩5 005.1ω2来平衡往复惯性力Pj,此剩余力与Y轴(气缸中心线方向)夹角为51.2°。
此时,剩余离心力与往复惯性力Pj的合力F在X、Y轴方向的投影为:

α为曲轴转角,取α为0°~360°CA之间的一系列值(如表1所示),可得出如图5所示实际情况的一条椭圆曲线。可见某小型通用发动机惯性力椭圆是一个细长的扁扁的椭圆,其长轴与气缸中心线夹角(Y轴)为31°左右,即发动机剧烈振动方向偏向气缸中心线(Y轴)方向,而转移到其它方向很小,所以造成整机明显振动。
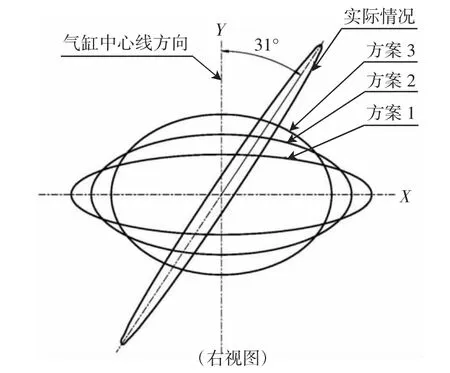
图5 α为0°~360°CA时的椭圆曲线

表1 α为0°~360°CA时的FX和FY值
3 改进方案及对策
一般总是希望椭圆的长轴方向(惯性力大的方向)放在发动机刚度较大的方向或吸振能力较好的方向。根据此原则再结合某小型通用发动机在整机上的布置,又考虑改进方案的经济性[3],可以采用在尽可能最少改变现有结构下的3种方案,其惯性力椭圆曲线如图5所示。即希望把往复惯性力Pj由Y轴(气缸中心线)转移一部分至X轴(坐垫方向上)。X轴方向上的力可以通过整机上的减振弹性元件来克服,这样可以大大减轻整机的振动,改善平顺性和舒适性。至于转移量的多少,可以通过实验手段得出最佳值。
根据平衡质量离心力平衡掉旋转质量的离心力Pr后与往复惯性力Pj的合力在X、Y轴上的投影公式(如图2所示):
Y轴方向:FY=Pj-ΔP cosα=9505.6ω2cosα-ΔP cosα
X轴方向:FX=ΔP sinα
3.1 方案一
设ΔP=2 000ω2
即FY=9 505.6ω2cosα-2 000ω2cosα=7505.6ω2cosα
FX=2 000ω2sinα
可以得出如图5所示的惯性力椭圆曲线,此时椭圆长轴方向(惯性力大的方向)已朝向X轴方向(坐垫方向),正是合理振动方向。
要ΔP=2 000ω2,就必须对现有曲柄的平衡质量进行重新布置,通过Pro/E软件的三维造型及模型分析功能,可以求出平衡质量。
3.2 方案二
同理设ΔP=3 000ω2
即FY=9505.6ω2cosα-3 000ω2cosα=6505.6ω2cosα
FX=3 000ω2sinα
3.3 方案三
同理设ΔP=4 000ω2
即FY=9 505.6ω2cosα-4 000ω2cosα
=5 505.6ω2cosα
FX=4 000ω2sinα
4 结论
1)对于小型通用发动机而言,由于结构的限制,采用转移法来平衡一阶往复惯性力虽然达不到完全平衡,但最大的优点是结构紧凑,经济实用。
2)惯性力的大小对振动固然重要,但惯性力的方向和频率在设计中也是需要重点考虑的因素。根据实验结果[4],方案三的措施最为有效,明显地改善了振动,取得了令用户满意的效果。
