高速动车组闸片寿命分布和检查周期的探讨*
2019-03-18张一喆王彩霞
张一喆, 李 强, 王彩霞
(1 北京交通大学 载运工具先进制造与测控技术教育部重点实验室, 北京 100044; 2 北京京港地铁有限公司 技术工程, 北京 100068)
随着2018年8月京津城际开行十周年之际,该线路全部更换为新型动车组“复兴号”运营,并且恢复350 km/h速度。更多的线路将逐步达到速度350 km/h。速度的提升,无疑对车辆系统各个部分的安全性和可靠性提出了更高的要求[1]。
京津城际是我国最早开通的350 km/h速度等级的高速铁路。由于站间距较小,频繁地折返和启停,导致京津城际运营的CRH3C型高速动车组,在所有暴露出的薄弱环节中,车辆磨耗件磨损加快成了较为突出的一大问题[2]。该车自投入运营以来,一级修中闸片的消耗量极为庞大,而粉末冶金闸片价格又非常昂贵,加上频繁检测所耗费的工人工时,大大提升了动车组的运用成本[3-4]。
从目前来看,我国对于动车组闸片一类的关键部件逐渐从故障修过渡到预防修,即周期性对零部件进行检修更换。而检修周期的确定,又多借鉴于供货商的建议以及一些其他客户反馈的信息,比较少结合自身运用的线路情况、交路情况、检修条件等诸多复杂因素[5-6]。这样往往会导致过度维修或者是维修不足,前者带来的是运营成本的大幅度提高,而后者往往会埋下安全隐患[7]。
通过实际数据分析,得到了动车组闸片的寿命分布模型,建立了确定检修周期常用的模型,为解决修程修制中的实际问题提出了新的方案。
1 寿命的威布尔分布及其参数估计
1.1 寿命预测常用方案
对于某些机械零部件的寿命预测,通常采用试验和计算模拟的方法[8]。
对于闸片,可以先期通过实测得到闸片厚度与时间历程的关系,来长期跟踪统计闸片的使用寿命。或者是做有限元的仿真,得到制动盘和闸片的响应,计算动应力进行寿命预估。但这些方案通常耗时过长或者过于依赖边界条件的处理以及一些比较难以把握的因素,从而导致获得的结果可信度较差。综上原因,故可先对样本做分布拟合来估计寿命。
1.2 闸片三参数威布尔分布模型
通常情况下,动车组闸片在投入使用一段时间内不会发生失效。闸片的主要失效方式是磨损,而威布尔分布适用于因腐蚀、磨损、疲劳而强度受损的设备和零部件。这些故障数据经过威布尔变换后在威布尔概率纸上呈现的不再是直线,此时采用三参数威布尔分布对其失效时间t(即寿命)进行拟合尤为合适[9]。
三参数威布尔分布的累积分布函数如下[10]:
(1)
概率密度函数如下:
(2)
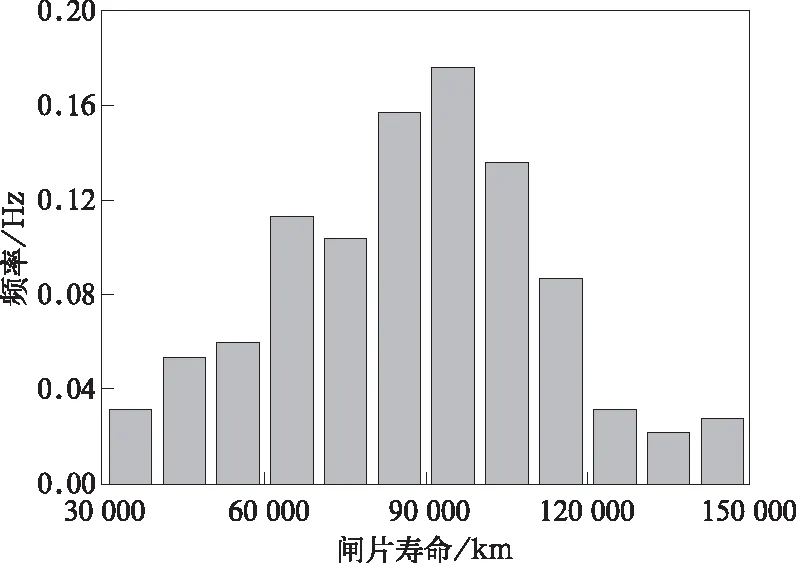
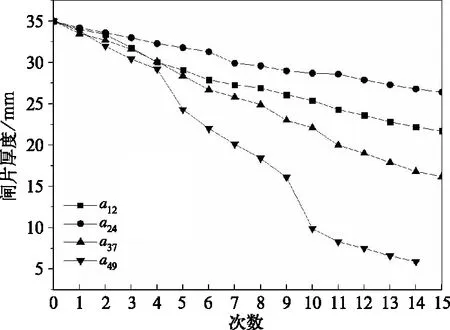
式中:t为适用于威布尔分布的设备或零部件的使用寿命,γ为曲线的位置参数,θ为尺度参数,β为形状参数,在上两式中有:θ>0,β>0,0<γ 三参数威布尔分布有多种参数估计方法,其中较为常用的有极大似然法,概率权重矩法,双线性回归法,灰色估计法,相关系数优化法等[11-12]。根据文献[13]建议,对于大样本,采用极大似然法或者双线性回归法拟合效果较好,工程上最常用极大似然法做参数估计。 现假定容量为n的样本T=[t1,t2,…tn]服从三参数威布尔分布,则其对数似然函数如下: lnL(β,θ,γ)=nlnβ-nβlnθ+ (3) 现对上式中的尺度参数θ求偏导,有: (4) 令θ偏导数等于0,解得: (5) 现将如上结果带入式(3),则其似然函数如下: (6) 根据极大似然原理,使似然函数取得极大值的(β,γ)即为参数点估计值。显而易见,式(6)为非线性方程,无法直接获得解析解。此类非线性问题数学上多采用Newton-Raphson迭代法[14],在matlab中较为容易实现,对于威布尔分布的参数估计问题,在多次迭代之后能够获得相当理想的结果。 目前京津城际动车组闸片检测更换项目安排在隔日进行的每次一级检修中,即仪器逐一测量厚度。所采用的某型闸片的初始厚度为35 mm,使用后经检测,如果厚度小于等于最低磨耗限度5 mm时,便进行更换。 本例中的数据来自于京津城际运营的CRH3C动车组某一列4辆拖车。由于每辆车共有12对闸片,故有48组拖车闸片位置。目前获得该动车组近3年多以来所有闸片位置两次更换之间的运行里程数,共有954组,部分位置数据如下: a11=( 92572 83769 48992 64031 97729 85274 60270 78954 100484 114776 87546 135709 95351 58045 73225 73079 102088 123167 94350 107589 108472); …… a34=( 58736 115798 127131 86984 81269 91580 72488 93472 120873 69850 73585 82143 39762 90350 103146 135072 92468 101625 83594); a35=( 102479 73851 116304 84831 89476 46820 117462 93075 100484 128631 97521 96334 60351 145709 95934 97804 76897 123167 97254);…… 其中,a11表示第1辆拖车1位闸片,a34表示第3辆拖车4位闸片。图1为闸片寿命的频率直方图,可以看出在90 000 km附近更换的闸片数量较多,超过120 000 km以及小于40 000 km磨耗到限的闸片比较少。 图1 闸片寿命分布频率直方图 采用极大似然法对闸片寿命数据的3参数威布尔分布模型进行参数估计。将闸片寿命数据带入1.3节中的对数似然方程,用Newton-Raphson迭代法求解,得到γ=17 126,β=3.1,θ=79 241。则其可靠度函数为: (7) 图2 闸片寿命分布的可靠度函数曲线 图2给出了闸片寿命分布的可靠度函数曲线。图中粗线是与之对照的寿命经验分布函数图线,即对第2.1节样本中所有点累积得到的可靠性曲线。可以看出两条曲线比较接近。 为了进一步检验模型的选择和拟合的效果,选择K-S检验法进行优度检验。K-S检验法是可靠度分析中的常用检验方法,它比χ2检验等方法得到结果更加直接和准确[9]。 具体方案是将n个测试数据按照由小到大的顺序排列,根据假设分布,计算得到每个数据所对应的R0(ti),再将其与数据的经验分布函数Rn(ti)进行对比,所有差值的最大绝对值即为所检验统计量Dn的观察值。将Dn与临界值Dn,α作比较。若结果满足式(8),则接受原假设,反之拒绝。判定的具体表达式如下: Dn=sup|R0(ti)-Rn(ti)|=max{di} (8) 其中,R0(t)为上小节求得的可靠度函数,Rn(t)为样本的经验分布函数,Dn,α为显著性水平为α、样本容量为n时,Dn的拒绝临界值,d为经验分布与理论分布的差值。 计算得到Dn=0.028 6。查K-S检验临界值表,当n>50,显著度α=0.05时,Dn,α的近似值为0.044。则在该显著度下,接受样本服从威布尔分布的假设。可以得出对高速动车组闸片的可靠度分析,采用三参数威布尔分模型和本例中的参数估计方法比较合适。 建立检查周期计算模型,通常考虑可靠度、最大有效度以及经济性等因素[15]。对于高速动车组闸片这一类对安全性要求较高的间断工作、定期检修的冗余系统来说,其检修周期的确定,重点应该以可靠度为中心。 假设系统的检测更换周期,即修程中设计需要的无故障累计工作时间为T0,每次任务需要的持续时间为t,那么当系统寿命分布的可靠度函数已知时,系统的可靠度仅与T0和t有关。T0的取值与安全性和经济性密切相关,T0的增大,明显会使可靠度降低。 问题的实质就是系统在T0时刻不失效,并且在继续工作的时间t内仍不失效的条件概率,即: R0(t)=R(t|T0) (9) 由于有以古典模型导出的条件概率表达式: (10) 则式(9)可以写成如下形式: (11) 此式即为工程上,分析冗余系统在持续工作一定时间下的可靠度,常采用的数学模型[6]。在本例中,R0(t)为交路限定的持续里程,即任务持续时间t内可靠度的要求值,R(t|T0)为无故障累计工作里程为T0条件下的规定任务持续里程t内的可靠度,即条件可靠度。 结合京津城际的实际运用情况,每日运行里程约为1 600 km,通常隔日进行一次一级修,其中包含闸片检测一项。而一级修又是有条件检测闸片的最短间隔。故在目前修程中,有: T0=t=1 600×2=3 200 (12) 为了讨论隔日进行的一级修对闸片进行检测的必要性,即T0取值是否合适,将闸片寿命分布的可靠性函数式7)带入式(11),则有: (13) 参照现有的某些铁路标准[16-17],由于一个转向架上有6组闸片,即使某组闸片短时失效,不会有严重的安全隐患, 建议R0(t)大于0.999即可,在更加严苛的一些机械设计标准中[18],对于关键零部件,建议可靠度R0(t)取0.999 9。将两组数值代入,得到T0分别为23 414 km和17 998 km。结果说明,即使间隔18 000 km左右对闸片进行检测,依旧可以保证0.999 9的可靠度要求。结合京津城际动车组的运用交路特点,建议在闸片使用寿命前期,尝试每3次一级修或者是2次二级修(每3×104km进行)之间安排闸片检测即可保证足够的可靠度。 现以该CRH3C型动车组拖车48个位置2018年第1次更换的闸片数据为例,对延长检查周期的可行性作出分析。 针对京津城际的交路状况,文中提到,1次一级修的里程数即T0=3 200 km,18 000 km则可以包含5个完整的T0一级检修周期。新的检查周期按照5T0=16 000 km 制定,以3个检查周期,大约50 000 km的运用里程为例,分析新修程的风险性。 图3给出了3个检查周期,即15次一级修检查时部分闸片的厚度情况。 图3中看到,在使用里程大约50 000 km过程中,除了个别闸片厚度在两次检查间存在较大程度变化外,绝大多数闸片的使用里程和磨损量之间存在较好的线性关系。15次一级修后,全部的48组闸片中,a24位置的磨损量最少,剩余厚度为26.4 mm,而由于使用工况及自身缺陷等因素,仅有a49位置闸片在第14次一级修时测量其剩余厚度为5.9 mm,达到了更换的标准。 图3 一级修检查 由此看到,在本例中的时间周期内,进行15次闸片监测显然过于频繁。在以5T0为间隔,进行3次检查,仅会造成a49一例,晚于目前设定更换时间一个一级修周期,并且原有的修程中对更换厚度阈值还留有一定安全系数。按照闸片的新修程操作,对于提供足够制动力以及车辆安全行驶不会产生任何影响。 由动车段统计数据得知,京津CRH3C拖车闸片全寿命周期平均检查次数为27.7次,最多甚至达到了46次。如果按照文中提出的检查周期进行,则2次更换之间至多需要10次检测。 以京津城际上运用的某型动车组闸片使用寿命的研究为出发点,采用极大似然法进行参数估计,在牛顿迭代求解后得到闸片的可靠性函数。最后对其检修周期进行了讨论,得到了一定的条件可靠度下,闸片的检测更换周期。并用该车数据进行验证发现,采用新的检查周期后,对动车组的安全行驶不会造成影响。 从结果可以看出,满足可靠性要求的周期计算结果明显长于修程设计的检测周期,这便导致了一定程度上的过度检修以及资源和时间上的浪费。观察目前的高速动车组修程,通过文中的模型计算,还有一部分零件和设备的检测、维修以及更换的周期存在不合理之处。对此类问题,日后应该在本例模型基础上进行深入的探讨和研究,对不同运用特点的零部件按照其使用工况以及运用的线路特点等方面进行精细化模型的建立,对零件的维修和更换周期制定切合实际的标准,有较大的工程价值。1.3 参数估计方法
2 闸片可靠性模型的建立
2.1 闸片寿命数据统计
2.2 参数估计

2.3 拟合优度检验
3 基于可靠度的闸片检查周期
3.1 数学模型
3.2 实例分析
4 结 论
