权重引入对大型入户调查慢性病患病数据统计分析结果的影响

四川大学华西公共卫生学院(610041)

张 黎 陈芍兵 杨薛玉 张菊英△

为了以较低的调查成本获取具有代表性的样本,大型入户调查通常是多种基本抽样技术的结合使用,称为复杂抽样,如国家卫生服务调查、中国居民营养与健康状况调查[1]等。复杂抽样带来的不等概率问题导致抽样个体所代表的总体研究对象的个数并不相同[2]。同时,如果调查对象某些重要特征与总体的分布不一致,如年龄结构等,也会影响某些指标的估计。这时就需要对抽样个体赋以适当的权重,以期望得到一些重要指标的无偏估计。但是,目前我国大型卫生服务和健康调查采用的统计推断方法通常是建立在等概率随机抽样这一假设基础上,研究者普遍没有意识到在处理复杂抽样数据时忽略各抽样单位的权重以及人口结构时对分析结果的影响,对复杂抽样数据的处理方法缺乏正确的认识。

因此,本文将以2015年四川省分级诊疗需方调查数据为例,详述抽样权重的计算方法,并通过比较引入和不引入权重时的人口结构、参数点估计值以及统计推断结果的差异,说明权重的引入在处理大型入户调查数据时的必要性。

资料与方法

1.资料来源

资料来源于2015年四川省分级诊疗需方调查,权重的计算还利用了2015年四川省统计年鉴数据[3]和2010年四川省第六次人口普查数据[4]。

2.抽样方法

四川省分级诊疗需方调查采用多阶段分层整群随机抽样。调查以四川省城市分类[5](成都市和攀枝花市为一类地区,甘孜藏族自治州、阿坝藏族羌族自治州和凉山彝族自治州为三类地区,其余城市为二类地区)作为分层依据,分层后各阶段具体抽样单位、数量和方法见表1。

共调查14个区县,4141户,共11522人,具体样本分布见表2。

表1 各阶段的抽样单位、抽样数量和抽样方法

表2 调查样本分布

3.统计分析

本研究采用基础抽样权重、标准化权重以及比例校正权重的联合权重,通过比较加权前后人口结构、慢性病患病率以及两水平logistic回归模型结果,来探讨权重引入对人口结构、参数点估计值以及统计推断的影响。

(1)抽样权重的计算

①基础抽样权重

基础抽样权重即样本个体被抽中概率的倒数,若抽样方法为多阶段抽样,则为各阶段抽样权重之积[6]。

假设多阶段抽样中第一阶段到第四阶段的抽样权重分别为w1,w2,w3和w4,则基础抽样权重wbase=w1×w2×w3×w4。

②标准化权重

性别、年龄等人口学特征对指标估计有影响,进行标准化可以将样本人口结构有效地调整至总体的水平。标准化权重wstd具体计算方法见表3。

表3 标准化权重计算方法

wstd=PPrc/PSrc

其中,PPrc为总体中第r行第c列的人口数占总体人口总数的比例,PSrc为样本经过基础抽样权重加权后第r行第c列的加权人数占加权总人数的比例。

③比例校正权重

经过基础抽样权重和标准化权重联合加权之后权重之和与总体实际人口数有一定的偏差,需要比例校正权重再次加权。比例校正权重wadj即实际总体人数与样本加权后估计的总体人数之比。

④个体最终权重

个体最终的权重为基础抽样权重、标准化权重和比例校正权重的乘积。

wfinal=wbase×wstd×wadj

(2)两水平加权logistic回归模型

多水平模型可将随机误差分解到相应数据层次结构上,很好地解决了各观察值之间不相互独立的问题[7]。

logit(Pij)=(β0+u0j)+β1xij

u0j=β0j-β0

加权多水平模型综合了抽样理论与多水平模型理论,利用抽样权重减小不等概率抽样在参数估计中产生的偏倚,同时可以分析多个水平单位的影响[8]。加权多水平模型结构类似于一般多水平模型,但是其参数估计是构造加权对数伪似然函数如下[9-10]:

式中wj和wi|j分别为水平2和水平1的权重。

采用牛顿-拉夫逊最大算法求出上述参数估计值。个体水平权重如不经过缩放直接纳入模型,在参数估计时可能会产生偏倚。常用的权重缩放方法有两种[11-12]:

(3)统计分析软件采用STATA 14.0进行数据分析,检验水准为0.05。

结 果

1.权重计算结果

经事后分层,第一阶段 14个县区的抽样权重见表4。

Seminar属于开放性教学方式，充分利用工具书和大量的数据库资源，将学生的阅读范围有效扩大，使学生养成独立思考和分析问题的习惯。学生通过对文献资料进行阅读、分析、内化，使阅读的作用远远超过仅对某些概念和定义的了解，上升到对于学术观点的思考、评析和研究，学生的阅读占有资料能力得到了切实提高。

表4 第一阶段抽样权重结果

由于乡镇、街道等下级抽样单位的抽样信息不够完整,本研究在权重计算时视为两阶段抽样,第二阶段的抽样概率为样本人数与县区人数之比,具体结果见表5。

表5 第二阶段抽样权重结果

为了使人口结构与总体尽量保持一致,进一步以 2010 年人口普查的人口结构为参照进行分层-性别-年龄别标准化。以一类地区男性各年龄段为例,标准化权重结果见表6。

表6 一类地区男性标准化权重结果

经基础抽样权重以及标准化权重联合加权计算的各层人口总数与实际人口总数存在偏差,需要用比例校正权重作进一步校正。比例校正权重见表7。

表7 比例校正权重结果

根据四川省分级诊疗需方调查各级抽样框架及权重计算公式算得基础权重,再根据各层年龄-性别结构、人口比例校正之后,得出个体最终权重。

2.对人口结构的影响

表8为四川省第六次人口普查总体、未纳入权重时四川省分级诊疗需方调查样本以及纳入权重后的人口构成。与加权前相比,加权后四川省分级诊疗需方调查样本的年龄-性别构成更加接近普查总体。

人口金字塔可以更直观的反映人口分布特征。图1和图2分别是四川省分级诊疗需方调查(未加权)和四川省第六次人口普查人口金字塔。显然,相对于四川省第六次人口普查总体,四川省分级诊疗需方调查样本人口结构偏老龄化。图3是引入权重校正后的四川省分级诊疗需方调查人口金字塔,可见权重引入后的人口结构基本和四川省第六次人口普查数据保持一致。

表8 调查人口年龄-性别构成(%)

图1 四川省分级诊疗需方调查人口金字塔(未加权)

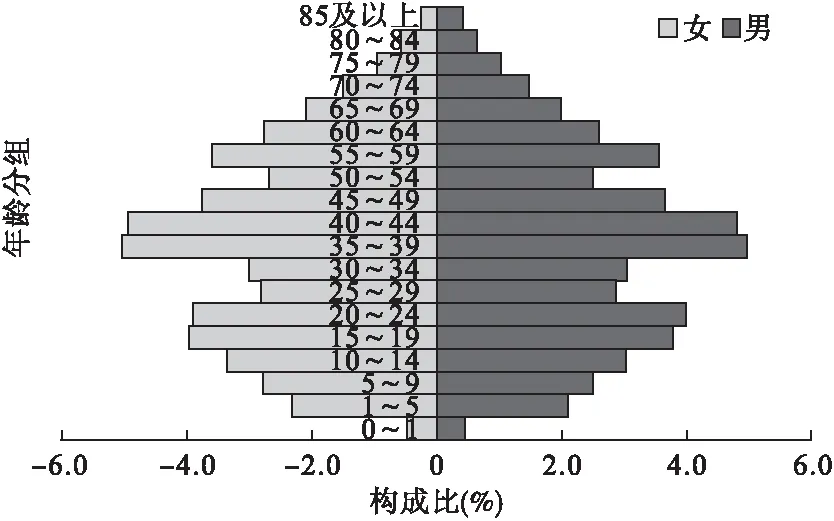
图2 四川省第六次人口普查人口金字塔

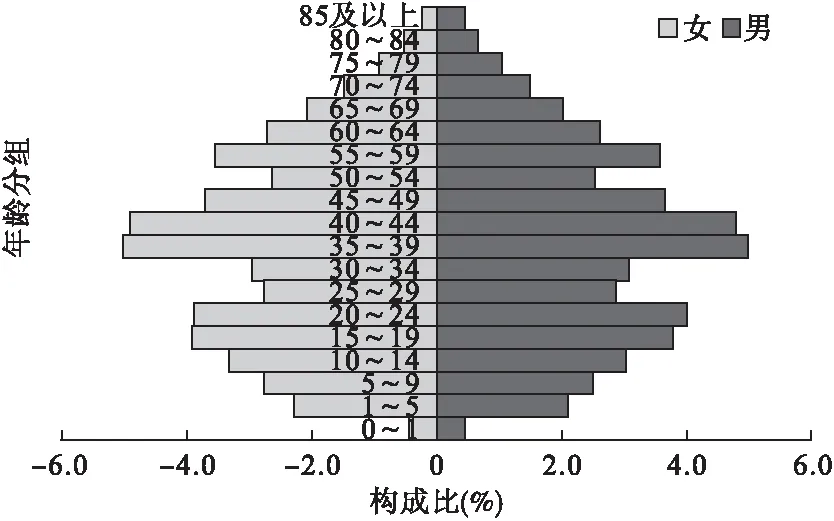
图3 四川省分级诊疗需方调查人口金字塔(加权)

3.对点估计值的影响

以15岁及以上居民的慢性病患病率为例说明权重引入对点估计值的影响。

慢性病患病率是指调查前半年内15岁及以上患病例数与15岁及以上调查总人数之比。加权前后四川省分级诊疗需方调查15岁及以上居民的慢性病患病率结果见表9。

表9 15岁及以上居民慢性病患病率(%)

2013年四川省卫生服务调查结果[13]显示,15岁及以上居民慢性病患病率为40.8%,城市地区(43.3%)高于农村地区(38.2%);不论是城市地区还是农村地区,四川省分级诊疗需方调查15岁及以上居民慢性病患病率均高于2013年四川省卫生服务调查结果。加权后,分级诊疗调查慢性病患病率明显下降,总慢性病患病率由原来的43.3%下降至29.6%,农村地区由41.5%下降至32.1%,城市地区下降更为明显,由45.1%下降至27.6%。表10展示了加权后分级诊疗需方调查中关于卫生服务需求和利用的一些其他的重要指标,如两周患病率、住院率和分级诊疗知晓率均有不同程度的下降。

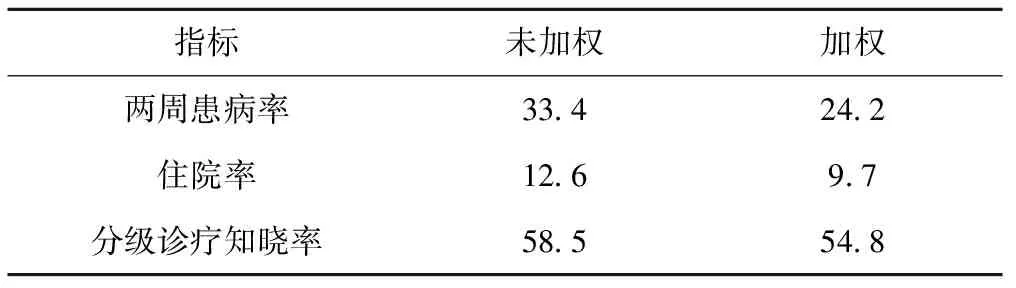
表10 分级诊疗需方调查重要指标(%)

4.对统计推断的影响

以四川省城市地区15岁及以上居民慢性病患病影响因素分析为例,说明权重的引入对统计推断的影响。分别拟合未引入权重的两水平logistic模型和加权两水平logistic模型,两种模型结果见表11。

表11 四川省城市地区15岁及以上居民慢性病患病影响因素分析两种模型结果对比

讨 论

本研究采用基础抽样权重、标准化权重以及比例校正权重的联合权重加权以后,四川省15岁以上居民慢性病患病率由未加权时的43.3% 变为29.6%,降幅明显。其他指标如两周患病率、住院率和分级诊疗知晓率均有不同程度的下降。这就提示我们,加权对于点估计值的影响非常之大。忽略权重、年龄、性别等人口学特征对各指标的影响,可能会带来错误的估计。目前,我国大型卫生服务和健康调查的分析报告通常只计算点估计值,如慢性病患病率、两周就诊率等指标,而年龄、性别等人口学特征会影响对这些重要指标的估计,因此权重的引入就显得十分必要。

相对于四川省第六次人口普查总体,四川省分级诊疗需方调查样本人口结构明显偏老龄化,可能是由于调查时间为2015年8-9月份,而四川省作为劳务输出大省[14],外出务工者一般在年底才会返乡,空巢现象严重;另外,由于本次调查是利用上班时间进行入户调查,城市地区抽中的年轻上班族家庭可能由于调查员多次入户无人在家错过本次调查而被其他家庭替代(样本备用户启用原则)。而权重引入后其人口结构基本和四川省第六次人口普查数据保持一致,说明权重的引入对全省人口结构起到很好的校正作用。

研究还发现,利用两水平加权logistic模型分析慢性病患病率的影响因素时大部分影响因素回归系数的P值增大,这与吕筠[2]等研究结果一致。部分系数的P值变化较大,例如加权后婚姻状况(已婚)的P值由0.719下降到0.016,基本医疗保险P值由0.333下降到0.034,按照0.05的检验水准,两者由不拒绝无效假设变为拒绝无效假设。而学历(高中/技校/中专)的P值由加权前的0.016变为加权后的0.155,由拒绝无效假设变为不拒绝无效假设。可见,在利用具有层次结构的大型入户调查进行统计推断时,忽略权重可能会得到完全相反的结论,做出错误的统计推断。

结 论

大型家庭入户调查为了节省人力物力,通常采用复杂抽样设计,但是由此造成的不等概率和数据的层次结构也给后期的数据分析带来一定的困难。如忽略不等概率某些重要指标可能会得到有偏的点估计,忽略数据的层次结构则可能会极大地降低标准误[15],从而可能得出错误的统计推断结论。因此针对大型家庭入户调查数据的统计分析,为了最大可能地降低复杂抽样所带来的影响,我们需要在方案设计阶段确定科学的抽样方案,并且完整地保存所有关于抽样过程的信息,尝试通过各类权重的校正方法联合计算最终权重,同时在数据分析阶段根据所研究的资料类型选择合适的统计分析模型和软件。